【数据结构】筛选法建堆
💞💞 前言
hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹
💥个人主页:大耳朵土土垚的博客
💥 所属专栏:数据结构
这里将会不定期更新有关数据结构的内容,希望大家多多点赞关注收藏💖💖
目录
- 💞💞 前言
- 1.建堆的方法
- 2.堆向上调整算法建堆及时间复杂度
- ✨堆向上调整算法
- ✨使用堆向上调整算法建堆
- ✨时间复杂度计算
- 3.筛选法建堆及时间复杂度
- ✨堆向下调整算法
- ✨使用堆向下调整算法建堆
- ✨时间复杂度计算
- 4.结语
1.建堆的方法
给你一个顺序表或数组(一串数据),通常来说建堆有两种方法一种堆向上调整算法,一种堆向下调整算法建堆也就是筛选法建堆。
筛选法建堆是一种快速建堆的方法,它是在堆排序算法中使用的。这种方法的基本思想是通过不断筛选节点,如果建大堆就将大的节点向上筛选,小的节点向下筛选,小堆就反之,最终得到一个有序的堆。
下面将以将数组int arr[] = {1,8,9,5,3,2}建成一个小堆为例介绍两种方法建堆
2.堆向上调整算法建堆及时间复杂度
✨堆向上调整算法
//向上调整算法
void AdjustUp( int* arr,int child)
{//找到双亲节点int parent = (child - 1) / 2;//向上调整while (child > 0){//如果父节点大于子节点就交换if (arr[parent] > arr[child]){Swap(&arr[parent], &arr[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}因为我们建的是小堆所以父节点肯定是要小于子节点的,所以当遇到父节点大于孩子节点就交换,相应的如果建的是大堆那么父节点小于孩子节点就交换
✨使用堆向上调整算法建堆
堆向上调整算法调整的是最后一个元素,前面的元素必须是一个堆,所以我们在使用堆向上调整算法时可以从一串数的第二个元素开始调整,它前面只有一个元素(一个元素就可以看成一个堆),调整完之后前面两个元素就是一个堆了,再从第三个元素开始调整,依此类推直到最后一个元素
图解如下:
int arr[] = {1,8,9,5,3,2}可以表示为:
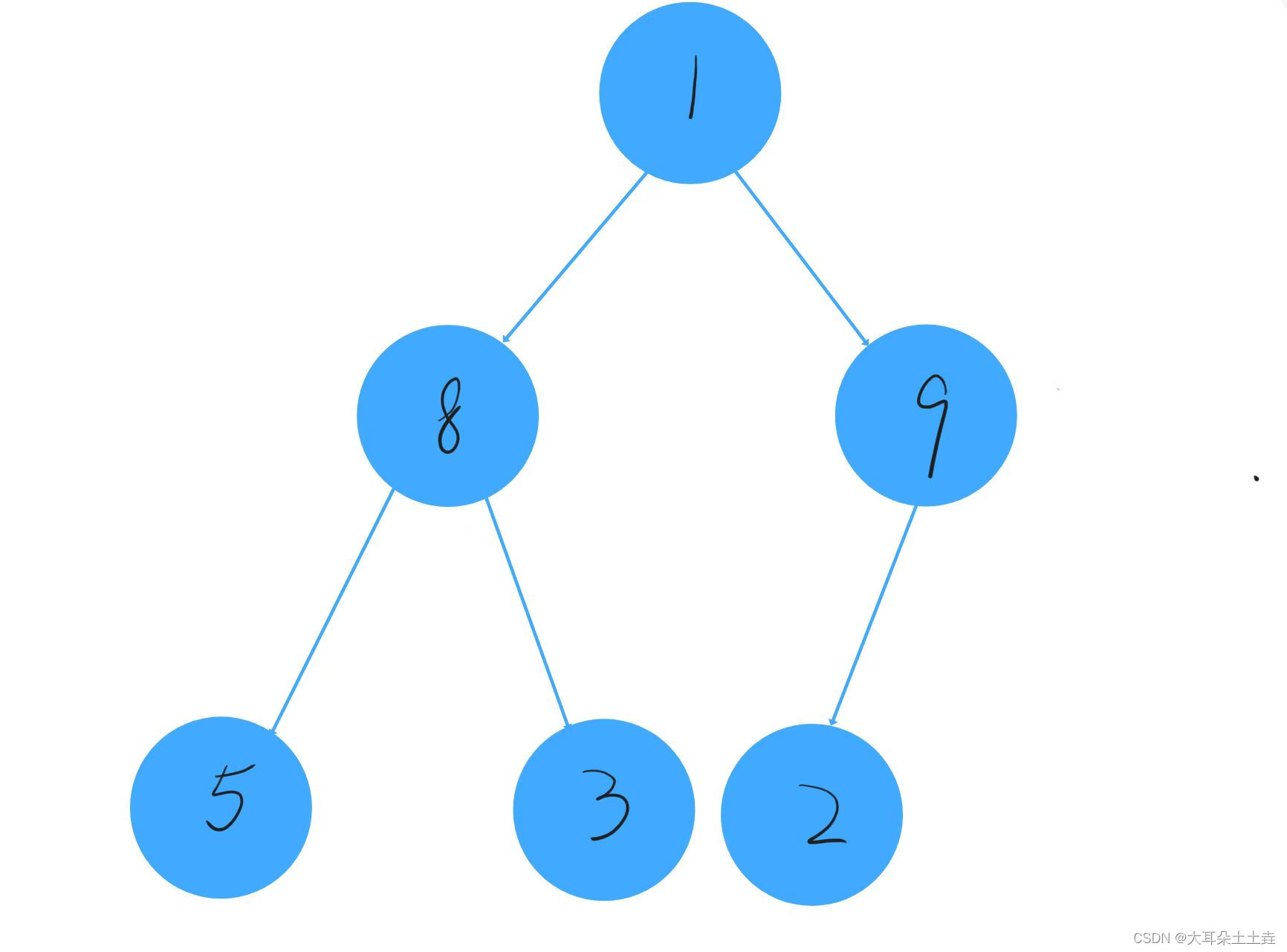
①第一个数据1可以看成一个堆,从第二个节点8开始向上调整,发现1<8,不需要交换:

②前面两个数据1和8已经构成小堆,从第三个元素开始向上调整,发现1<9不需要交换:

③前面三个数据已经构成小堆,从第四个数据5开始向上调整,发现5<8交换,交换后1<5,不需要交换:
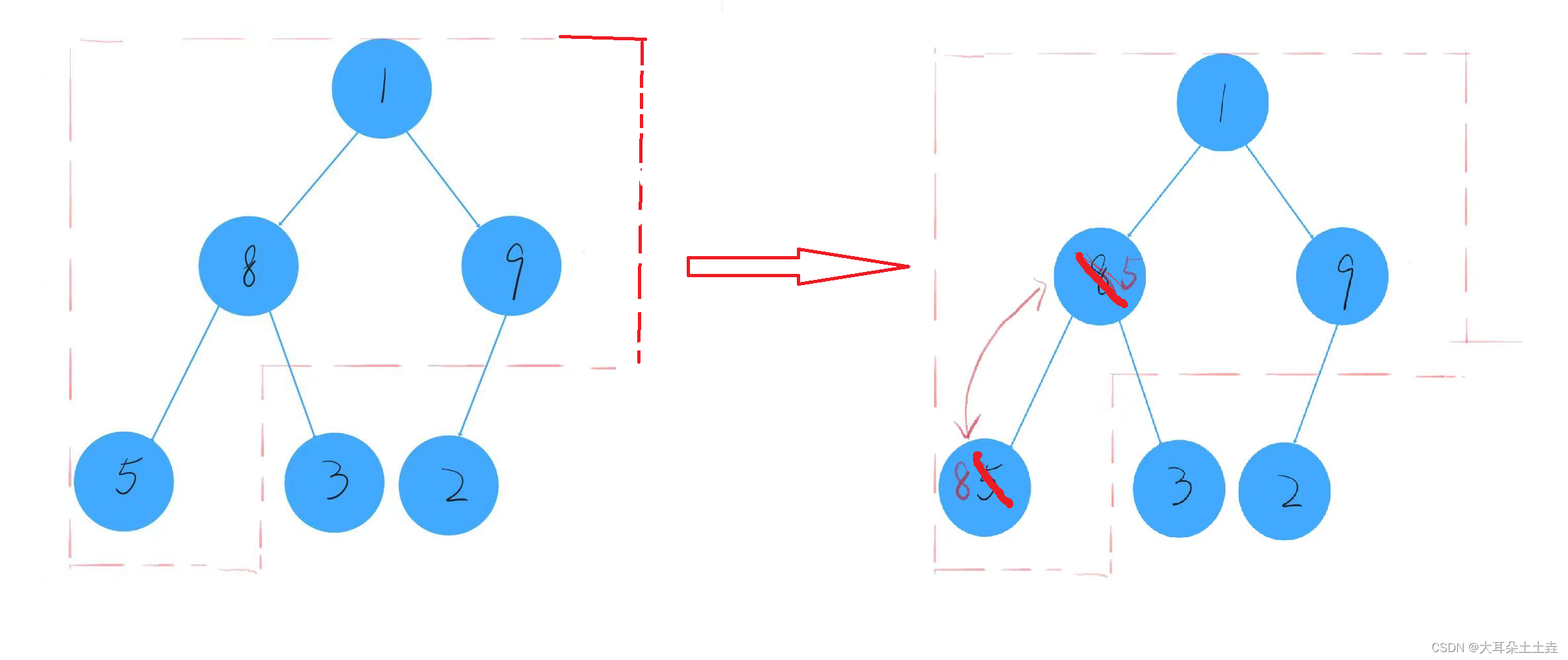
④前面四个数据构成小堆,从第五个数据3开始向上调整建堆,发现3<5交换,1>3不交换:

⑤前面五个数据构成小堆,从第六个数据2开始往上调整建堆,发现2<9交换,1<2不交换:

建好堆之后入下图:
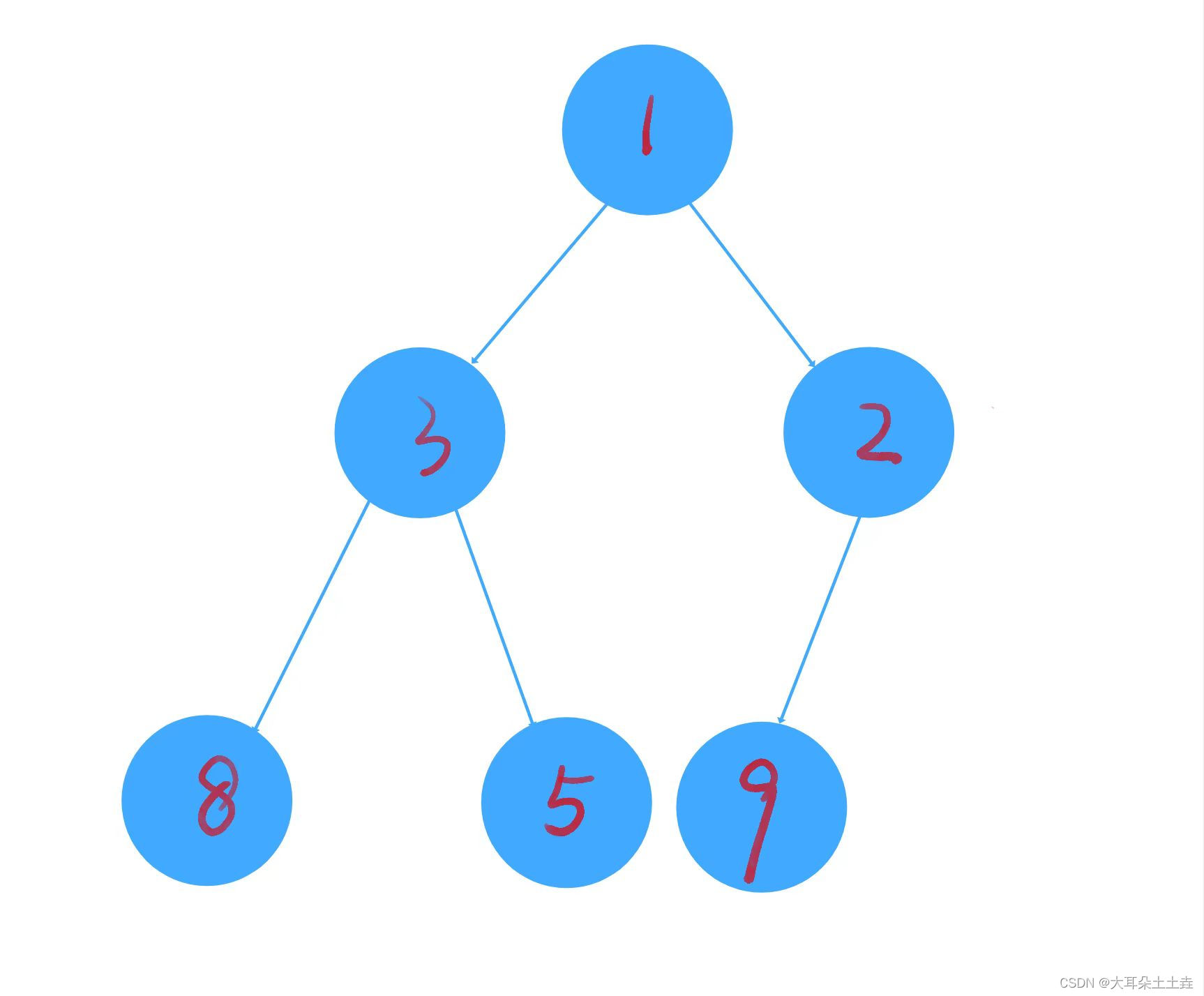
代码如下:
int main()
{int arr[] = { 1,8,9,5,3,2};//使用堆向上调整算法建堆,需要从第二个节点开始依次往上调整for (int i = 1; i < sizeof(arr)/sizeof(int); i++){AdjustUp(arr, i);}//打印数组for (int i = 0; i < sizeof(arr)/sizeof(int); i++){cout << arr[i] << " ";}return 0;
}
结果如下:

✨时间复杂度计算

由上图可知,堆向上调整法建堆的时间复杂度是NlogN
logN是以2为底的
3.筛选法建堆及时间复杂度
筛选法建堆需要利用我们的向下调整算法:
✨堆向下调整算法
//堆向下调整算法
void AdjustDown(int* arr,int n, int parent)
{//找到较小的孩子节点int child = parent * 2 + 1;//向下调整while (child < n){//找到较小的孩子节点if (child + 1 < n && arr[child] > arr[child + 1]){child++;}//如果父节点大于孩子节点就交换if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = child * 2 + 1;}elsebreak;}
}
✨使用堆向下调整算法建堆
具体步骤如下:
- 从完全二叉树中的最后一个非叶子节点开始,将其视为根节点。
- 从根节点开始,依次向下进行筛选,将当前节点与其左右子节点进行比较,将最大值上移。
- 完成一次筛选后,将当前节点的上一个节点作为新的根节点,再次进行筛选。
- 依次类推,直到所有节点都进行过一次筛选,最终得到一个有序的堆。
这里同样要注意,堆向下调整时,其节点左右子树必须是堆,我们从最后一个非叶子节点开始调整是因为其左右子树只有一个数据,可以看成堆
以int arr[] = {1,8,9,5,3,2}为例,图解如下:
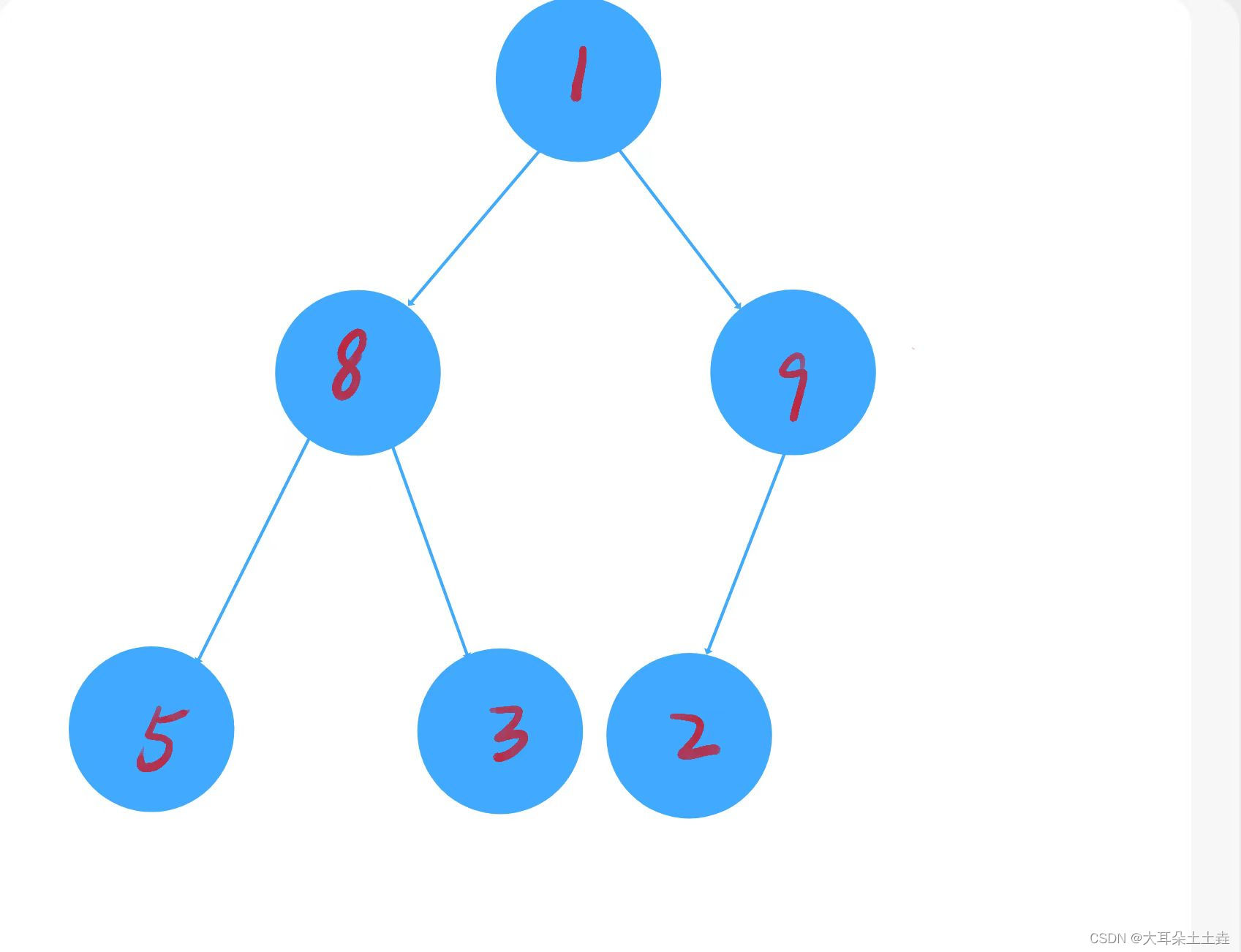
①从最后一个非叶子节点9开始往下调整,发现9>2交换:

②再从上一个节点8开始往下调整,先找到较小的孩子节点3,发现8>3交换:

③再从上一个节点1开始往下调整,找到较小的子节点2,发现1<2不交换:

小堆就建好了:

代码如下:
int main()
{int arr[] = { 1,8,9,5,3,2 };//使用堆向下调整算法建堆,需要从最后一个非叶子节点开始依次往下调整int size = (sizeof(arr) / sizeof(int) - 2) / 2;//找到最后一个非叶子节点下标for (int i = size; i >=0; i--){AdjustDown(arr, sizeof(arr) / sizeof(int),i);}//打印数组for (int i = 0; i < sizeof(arr) / sizeof(int); i++){cout << arr[i] << " ";}return 0;
}
结果如下:
我们发现堆向下调整需要多传一个参数数据个数n,这是因为向下调整时,最坏的情况下会一直向下调整到最后一个节点,此时要控制下标不能越界,所以要传数据个数来防止越界,而前面的向上调整最坏的情况下,会调整到根节点,只需要其下标不小于0就不会越界,所以不需要传参数n
✨时间复杂度计算

由上图可知,堆向下调整法建堆的时间复杂度是N
4.结语
由上述时间复杂度的分析可知,我们最好选用筛选法也就是堆向下调整算法建堆,以上就是今天所有的内容啦~ 完结撒花~ 🥳🎉🎉
相关文章:

【数据结构】筛选法建堆
💞💞 前言 hello hello~ ,这里是大耳朵土土垚~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 💥个人主页&#x…...
DevExpress Installed
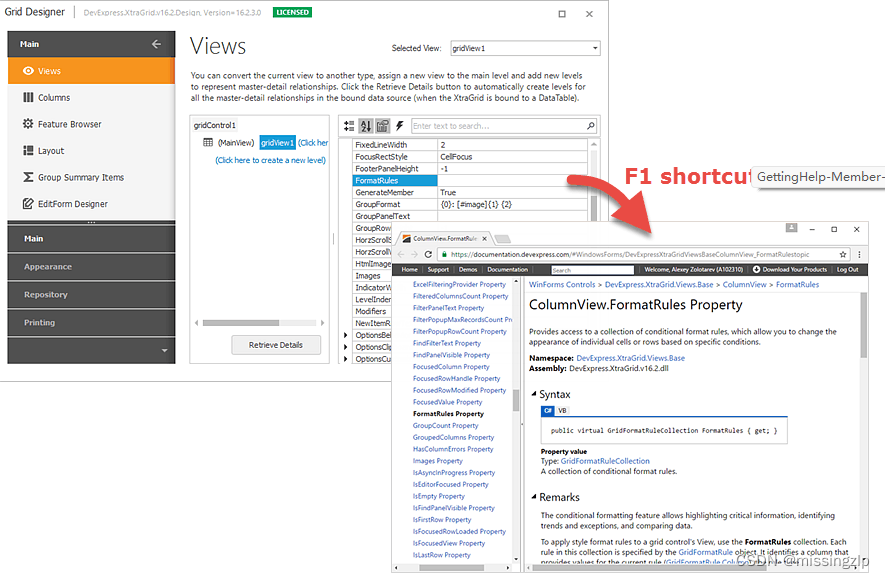
一、What’s Installed 统一安装程序将DevExpress控件和库注册到Visual Studio中,并安装DevExpress实用工具、演示应用程序和IDE插件。 Visual Studio工具箱中的DevExpress控件 Visual Studio中的DevExpress菜单 Demo Applications 演示应用程序 Launch the Demo…...

解决QT QMessageBox 弹出需点击两次才能关闭问题
放个链接不迷路:添加链接描述...

Milvus--向量数据库
Milvus 是一个开源的向量数据库,专为高维向量数据的存储、查询和检索而设计。它支持多种类型的向量数据,如浮点数向量、整数向量等,并且提供了强大的向量相似度计算功能。Milvus采用分布式架构,可以轻松地扩展到大规模数据集&…...

php质量工具系列之PHPCPD
PHPCPD 用于检测重复代码,直观的说就是复制粘贴再稍微改改 该工具作者已经 停止维护 安装 composer global require --dev sebastian/phpcpd执行 phpcpd --log-pmd phpcpd_result.xml ./app参数介绍 --log-pmd 将结果保存在phpcpd_result.xml 中 ./app 是phpcpd扫…...
Android14 WMS-窗口绘制之relayoutWindow流程(二)-Server端
本文接着如下文章往下讲 Android14 WMS-窗口绘制之relayoutWindow流程(一)-Client端-CSDN博客 然后就到了Server端WMS的核心实现方法relayoutWindow里 WindowManagerService.java - OpenGrok cross reference for /frameworks/base/services/core/java/com/android/server…...

安全测试 之 安全漏洞:SQL注入
1. 背景 持续学习安全测试ing,安全测试是在IT软件产品的生命周期中,特别是产品开发基本完成到发布阶段,对产品进行检验以验证产品是否符合安全需求定义和产品质量标准的过程。也就是说安全测试是建立在功能测试的基础上进行的测试。 2. SQL…...

CUDA和驱动版本之间的对应关系
这个之前总结过,可是不太好找,专门写一篇博客再总结一下: 1. CUDA 12.5 Release Notes — Release Notes 12.5 documentation 相信很多朋友有一样的需求。...
问题总结及解决方法)
MDK(μVsion3)问题总结及解决方法
问题 1:MDK 工具的 CARM 编译器? 我原来对 CARM 编译器比较熟悉,想用 CARM 编译器编译工程,但是却弹出一个不能执 行“cc”的错误,到 KEIL 网站查下才知道原因:由于 CARM 编译器是比较老的编译器࿰…...
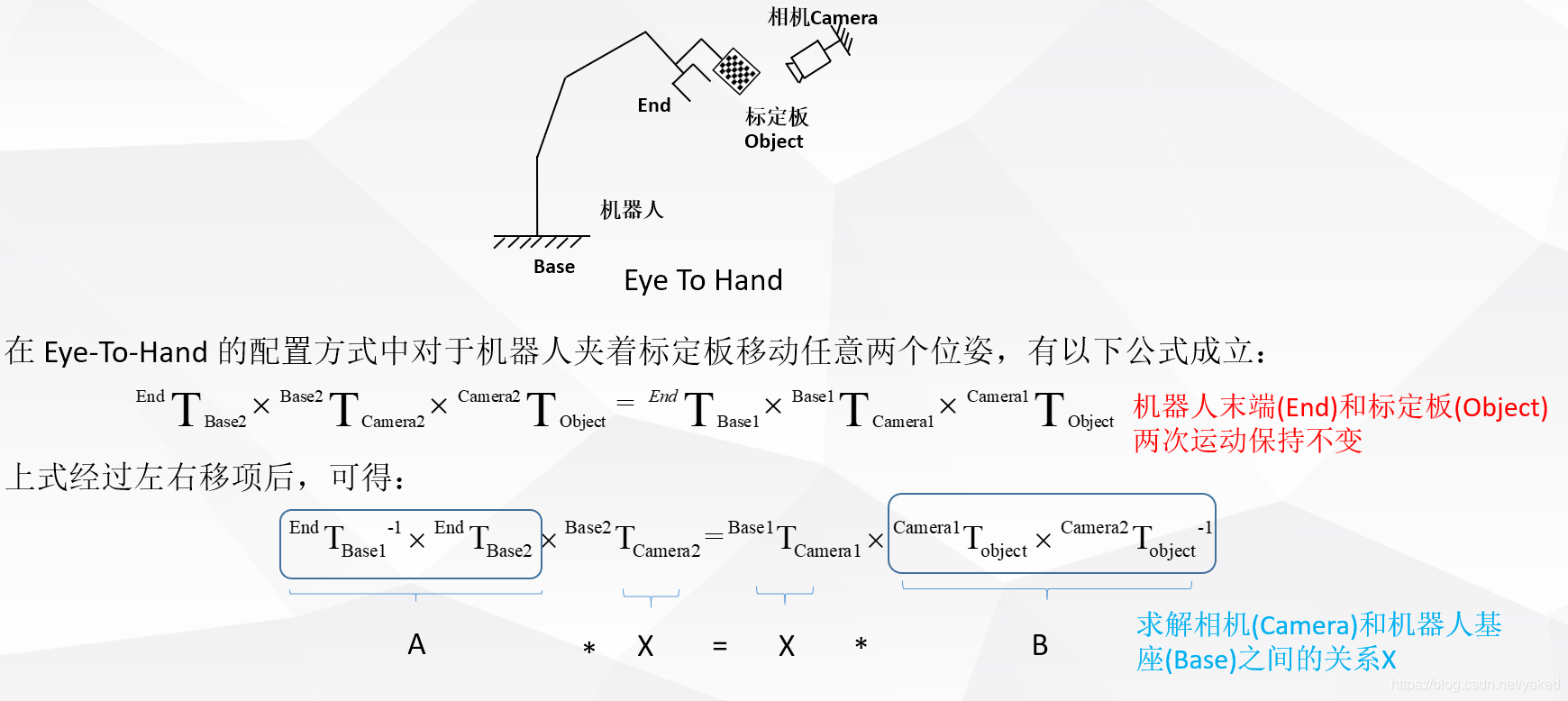
手眼标定学习笔记
目录 标定代码: 手眼标定原理学习 什么是手眼标定 手眼标定的目的 eye in hand eye to hand AXXB问题的求解 标定代码: GitHub - pumpkin-ws/HandEyeCalib 推荐博文: https://zhuanlan.zhihu.com/p/486592374 手眼标定原理学习 参…...

Dell戴尔XPS 16 9640 Intel酷睿Ultra9处理器笔记本电脑原装出厂Windows11系统包,恢复原厂开箱状态oem预装系统
下载链接:https://pan.baidu.com/s/1j_sc8FW5x-ZreNrqvRhjmg?pwd5gk6 提取码:5gk6 戴尔原装系统自带网卡、显卡、声卡、蓝牙等所有硬件驱动、出厂主题壁纸、系统属性专属联机支持标志、系统属性专属LOGO标志、Office办公软件、MyDell、迈克菲等预装软…...
【第8章】SpringBoot实战篇之文章分类(上)
文章目录 前言一、后端代码1. CategoryController2. service3. CategoryMapper4. Category 二、测试1. 失败(校验)2.正常 总结 前言 从这开始进入文章相关的接口开发,本章主要介绍定义文章分类接口和新增文章分类 建表语句和测试用例,在SpringBoot专栏首…...

【QT】Qt Plugin开发
目录 插件是什么QT插件是什么 为什么要有插件开发插件开发优势插件和动态库区别 Qt PluginQT插件类型QT插件开发流程QT插件应用QT插件JSON文件 参考文章 插件是什么 插件(Plug-in,又称addin、add-in、addon或add-on,又译外挂)是一种遵循一定规范的应用程序接口编写出来的程序。…...

快速了解GPU分布通信技术:PCIe、NVLink与NVSwitch
在现代高性能计算和深度学习领域,GPU的强大计算能力使其成为不可或缺的工具。然而,随着模型复杂度的增加,单个GPU已经无法满足需求,需要多个GPU甚至多台服务器协同工作。这就要求高效的GPU互联通信技术,以确保数据传输…...

Python对获取数据的举例说明
当使用Python来获取数据时,有许多不同的方法和库可以根据你的需求来选择。以下是一些常见的示例,说明如何使用Python来从各种来源获取数据。 1. 从网站或API获取JSON数据 你可以使用requests库从网站或API获取JSON格式的数据。例如,从某个API…...
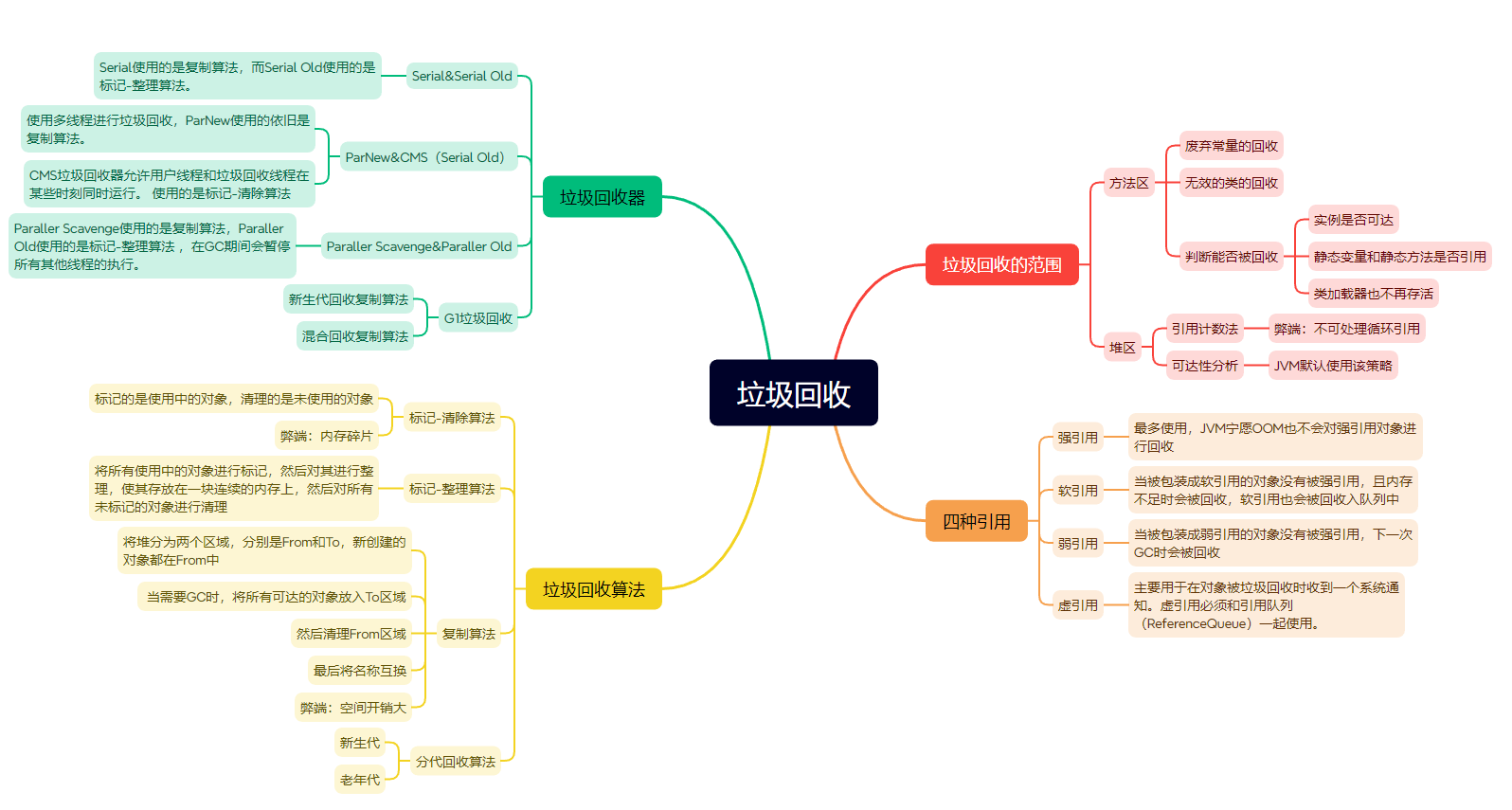
JVMの垃圾回收
在上一篇中,介绍了JVM组件中的运行时数据区域,这一篇主要介绍垃圾回收器 JVM架构图: 1、垃圾回收概述 在第一篇中介绍JVM特点时,有提到过内存管理,即Java语言相对于C,C进行的优化,可以在适当的…...

人工智能就业方向有哪些?
人工智能就业方向有哪些? 随着人工智能技术的不断发展,其应用领域也越来越广泛。对于想要进入人工智能领域的年轻人来说,选择一个合适的职业方向是至关重要的。今天给大家介绍六个热门的人工智能就业方向,分别是机器学习工程师、自然语言处理…...

自定义类型:枚举和联合体
在之前我们已经深入学习了自定义类型中的结构体类型 ,了解了结构体当中的内存对齐,位段等知识,接下来在本篇中将继续学习剩下的两个自定义类型:枚举类型与联合体类型,一起加油!! 1.枚举类型 …...

负载均衡加权轮询算法
随机数加权轮询算法 public int select() {int[] weights {10, 20, 50};int totalWeight weights[0] weights[1] weights[2];// 取随机数int offset ThreadLocalRandom.current().nextInt(totalWeight);for (int i 0; i < weights.length; i) {offset - weights[i];i…...
PyTorch 相关知识介绍
一、PyTorch和TensorFlow 1、PyTorch PyTorch是由Facebook开发的开源深度学习框架,它在动态图和易用性方面表现出色。它以Python为基础,并提供了丰富的工具和接口,使得构建和训练神经网络变得简单快捷。 发展历史和背景 PyTorch 是由 Fac…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

SQL进阶之旅 Day 22:批处理与游标优化
【SQL进阶之旅 Day 22】批处理与游标优化 文章简述(300字左右) 在数据库开发中,面对大量数据的处理任务时,单条SQL语句往往无法满足性能需求。本篇文章聚焦“批处理与游标优化”,深入探讨如何通过批量操作和游标技术提…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...

