二分+模拟,CF1461D - Divide and Summarize
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
Problem - 1461D - Codeforces
二、解题报告
1、思路分析
我们发现每次分裂操作结果都是固定的
我们从初始序列分裂出两个确定的子序列,两个确定的子序列又分裂出4个确定的子序列
那么也就是说我们最终能够分裂出的子序列的数目是O(n)的
我们预处理出所有的子序列就预处理出了所有可以得到的和(当然这个和要在分裂的过程中维护)
而分裂要求我们得到小于等于mid的部分和大于的部分
所以我们需要对原序列进行排序,模拟的过程通过二分来找到分裂的位置
同时预处理前缀和以便每次分裂前都记录一下当前得到的值
值得注意的是nums[l] = nums[r]的时候说明当前子序列是相同的,我们无法继续向下分裂
2、复杂度
时间复杂度: O(NlogN)空间复杂度:O(N)
3、代码详解
#include <bits/stdc++.h>
using PII = std::pair<int, int>;
using i64 = long long;
std::mt19937 rnd(std::chrono::steady_clock::now().time_since_epoch().count());const int P = [](int x) {auto isprime = [](int x) {if (x <= 1) return false;for (int i = 2; i <= x / i; i ++ )if (x % i == 0) return false;return true;};while (!isprime(x)) x ++;return x;
}(rnd() % 900000000 + 100000000);void solve() {/* 直接模拟 */int N, Q, s;std::cin >> N >> Q;std::vector<int> nums(N);std::vector<i64> pre(N + 1);for (int i = 0; i < N; i ++ ) std::cin >> nums[i];std::sort(nums.begin(), nums.end());for (int i = 0; i < N; i ++ ) pre[i + 1] += nums[i] + pre[i];std::vector<std::array<int, 2>> segs { { 0, N - 1 } }; segs.reserve(N);std::unordered_set<i64> st;while (segs.size()) {std::vector<std::array<int, 2>> nxt;for (auto& [l, r] : segs) {st.insert(pre[r + 1] - pre[l] + P);if (nums[l] != nums[r]) {int mid = std::upper_bound(nums.begin(), nums.end(), (nums[l] + nums[r]) >> 1) - nums.begin();nxt.insert(nxt.end(), { { l, mid - 1 }, { mid, r } });}}segs = std::move(nxt);}for (int i = 0, s; i < Q; i ++) {std::cin >> s;if (st.count(1LL * s + P))std::cout << "YES\n";elsestd::cout << "NO\n";}
}int main () {std::ios::sync_with_stdio(false); std::cin.tie(0); std::cout.tie(0);int _ = 1;std::cin >> _;while (_ --)solve();return 0;
}相关文章:

二分+模拟,CF1461D - Divide and Summarize
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 Problem - 1461D - Codeforces 二、解题报告 1、思路分析 我们发现每次分裂操作结果都是固定的 我们从初始序列分裂出两个确定的子序列,两个确定的子序列又分裂出4个确定的子序列 那么也就是说…...
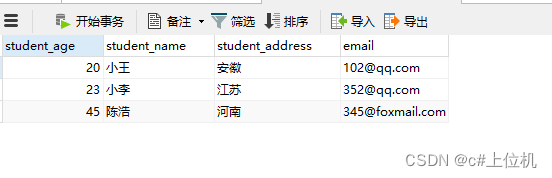
C#操作MySQL从入门到精通(16)——使用子查询
前言: 我们在查询数据的过程中有时候查询的数据不是从数据库中来的,而是从另一个查询的结果来的,这时候就需要使用子查询,本文使用的测试数据如下: 1、子查询 下面的代码就是先查询地址是安徽和广西的学生年龄,然后获取年龄对应的姓名 private void button__SubQuery…...
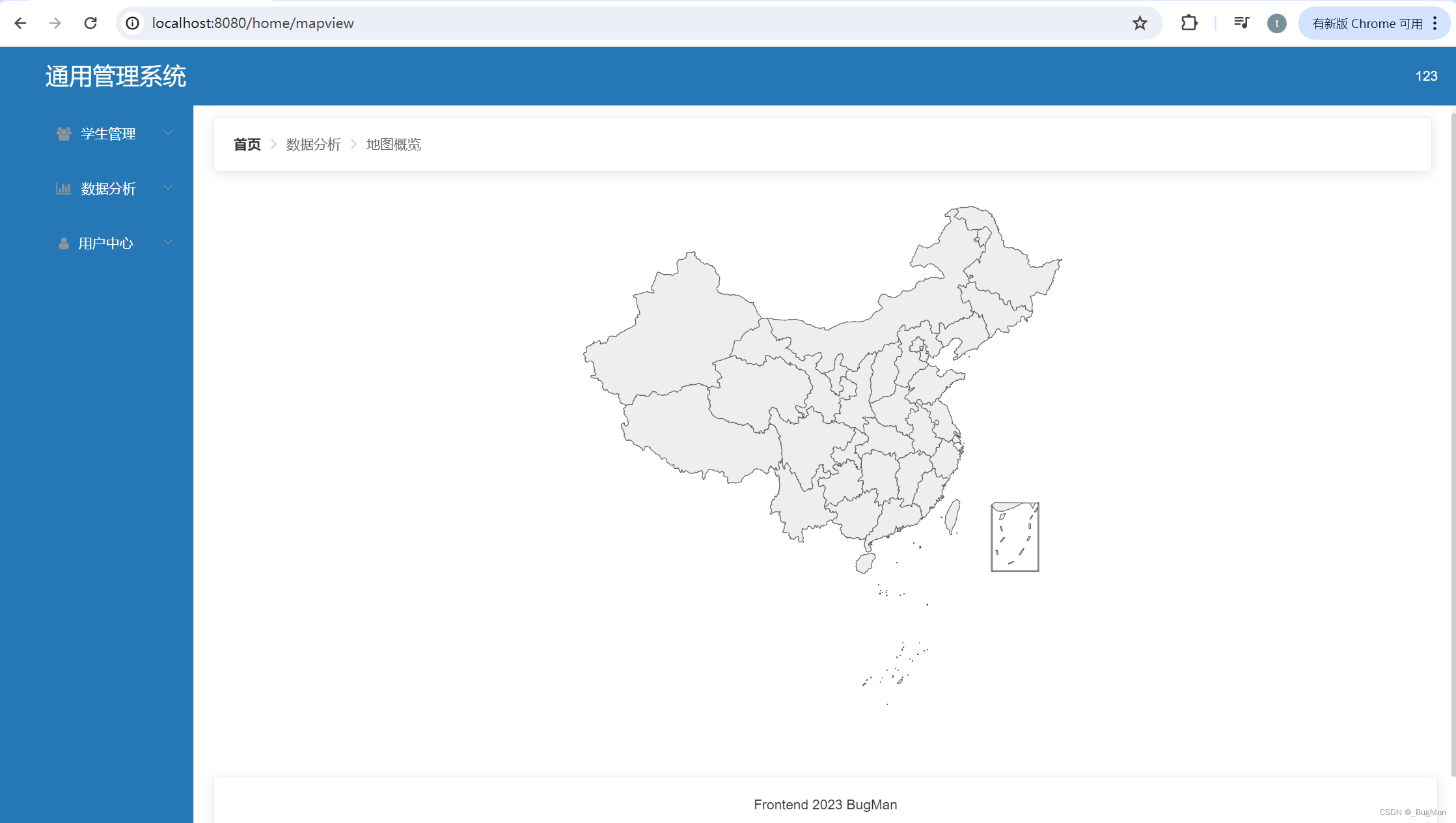
【vue实战项目】通用管理系统:图表功能
目录 前言 1.概述 2.数据概览页 2.1.柱状图 2.2.折线图 2.3.地图 前言 本文是博主前端Vue实战系列中的一篇文章,本系列将会带大家一起从0开始一步步完整的做完一个小项目,让你找到Vue实战的技巧和感觉。 专栏地址: https://blog.csd…...
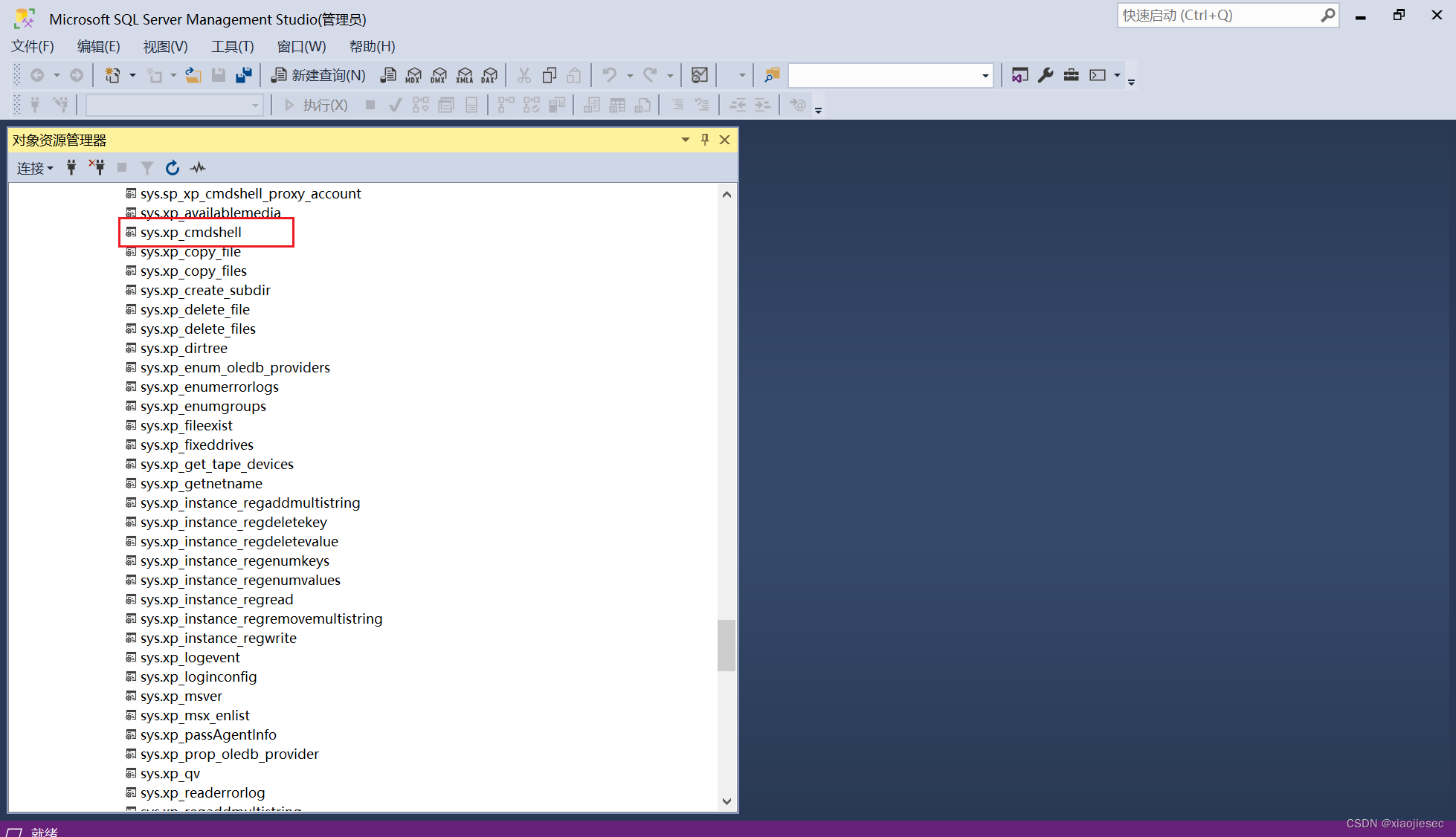
第99天:权限提升-数据库提权口令获取MYSQLMSSQLOracleMSF
案例一:提权条件-数据库帐号密码获取方式 提权条件 - 数据库帐号密码获取方式 0 、网站存在高权限 SQL 注入点 1 、数据库的存储文件或备份文件 2 、网站应用源码中的数据库配置文件 3 、采用工具或脚本爆破 ( 需解决外联问题 ) sql注入点 xhcms后台管理系统…...

Java 环境配置 -- Java 语言的安装、配置、编译与运行
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 002 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...
升级最新版openssh-9.7p1及openssl-1.1.1h详细步骤及常见问题总结
近期因为openssh相继被漏洞扫描工具扫出存在漏洞,所以考虑升级操作系统中的openssh和openssl为最新版本,来避免漏洞风险。期间的升级过程及遇到的疑难问题,特此记录下来,供有需要的人参考。 本次目标是升级 openssh 为 9.7p1 版本…...

学习使用 Frida 过程中出现的问题
一、adb shell命令报错:error: no devices found 目前该问题解决方法仅供参考,可先看看再选择试试!!!!! 查看此电脑也会发现没有出现手机型号文件夹。 第一步: 检查一下手机开了u…...

Java实现简单词法、语法分析器
1、词法分析器实现 词法分析器是编译器中的一个关键组件,用于将源代码解析成词法单元。 词法分析器的结构与组件: 通常,词法分析器由两个主要组件构成:扫描器(Scanner)和记号流(Token Stream&a…...

Python实现半双工的实时通信SSE(Server-Sent Events)
Python实现半双工的实时通信SSE(Server-Sent Events) 1 简介 实现实时通信一般有WebSocket、Socket.IO和SSE(Server-Sent Events)三种方法。WebSocket和Socket.IO是全双工的实时双向通信技术,适合用于聊天和会话等&a…...
)
python中的解包操作(*和**)
在Python中,* 和 ** 用于函数定义和函数调用时的参数解包和传递,它们有不同的用途和作用。以下是它们的详细解释和区别: 单星号 (*) 1. 位置参数解包(函数调用) 在函数调用时,* 用于将列表或元组解包成位…...

Lua 时间工具类
目录 一、前言 二、函数介绍 1.DayOfWeek 枚举定义 2.GetTimeUntilNextTarget 3.GetSpecificWeekdayTime 三、完整代码 四、总结 一、前言 当我们编写代码时,我们经常会遇到需要处理日期和时间的情况。为了更方便地处理这些需求,我们可以创建一个…...
)
Qt——Qt网络编程之TCP通信客户端的实现(使用QTcpSocket实现一个TCP客户端例程)
【系列专栏】:博主结合工作实践输出的,解决实际问题的专栏,朋友们看过来! 《项目案例分享》 《极客DIY开源分享》 《嵌入式通用开发实战》 《C++语言开发基础总结》 《从0到1学习嵌入式Linux开发》 《QT开发实战》 《Android开发实战》 《实用硬件方案设计》 《结构建模设…...

Qt信号槽与函数直接调用性能对比
1. 测试方法 定义一个类Recv,其中包含一个成员变量num和一个成员函数add(),add()实现num的递增。 另一个类Send通过信号槽或直接调用的方法调用Recv的add函数。 单独开一个线程Watcher,每秒计算num变量的增长数值,作为add函数被调…...

Python中的异常处理:try-except-finally详解与自定义异常类
Python中的异常处理:try-except-finally详解与自定义异常类 在Python编程中,异常处理是确保程序健壮性和可靠性的重要部分。当程序遇到无法预料的错误时,异常处理机制能够防止程序崩溃,并允许我们采取适当的措施来解决问题。本文…...
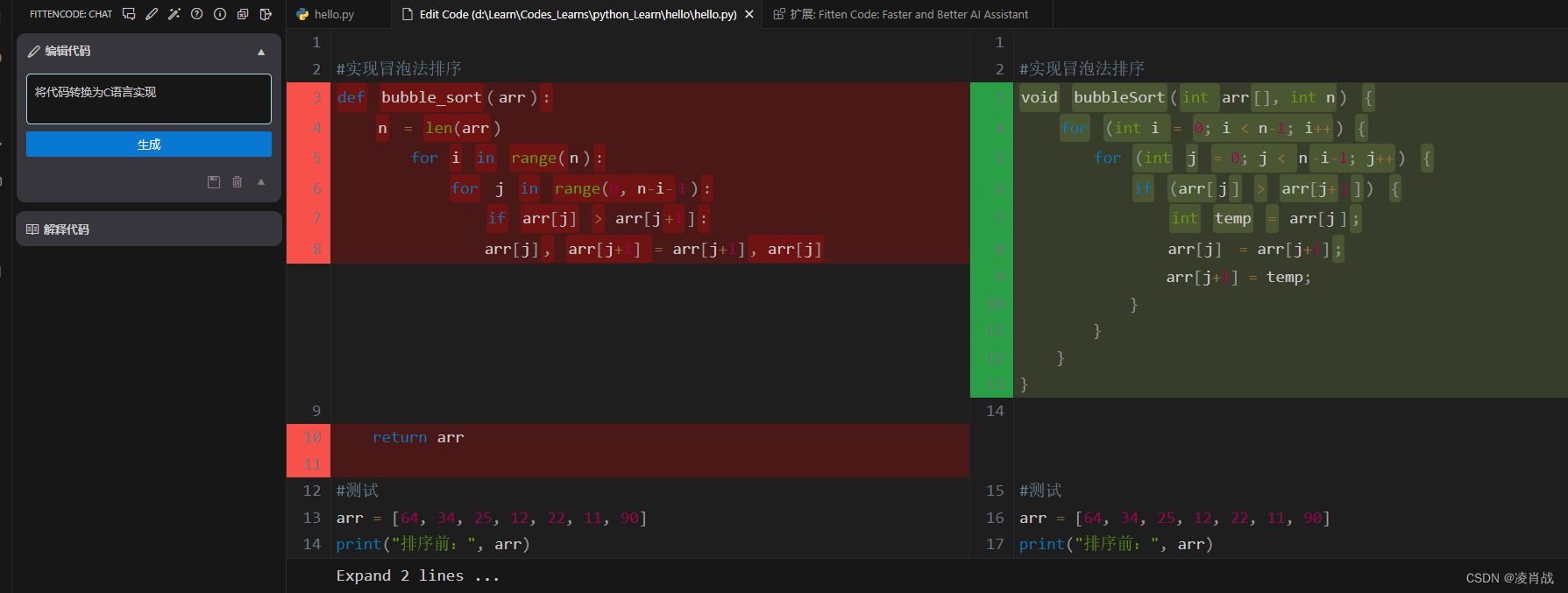
vscode软件上安装 Fitten Code插件及使用
一. 简介 前面几篇文章学习了 Pycharm开发工具上安装 Fitten Code插件,以及 Fitten Code插件的使用。 Fitten Code插件是是一款由非十大模型驱动的 AI 编程助手,它可以自动生成代码,提升开发效率,帮您调试 Bug,节省…...

人工智能小作业
1.问题 将下列句子用一阶谓词形式表示: (1)雪是白的。 (2)数a和数b之和大于数c。 (3)201班的学生每人都有一台笔记本电脑。 2.答案 句子(1)“雪是白的”可以表示为: White(雪)。 句子(2)“数a和数b…...

程序员搞副业一些会用到的工具
微信号采集(爬虫)技术的选型 那么,我们应该使用什么技术来从庞大的网页内容中自动筛选和提取微信号呢?答案就是:数据采集技术,也就是爬虫技术。 然而,数据采集技术种类繁多,我们具体应该采用哪一个呢&…...

k8s更改master节点IP
背景 搭建集群的同事未规划网络,导致其中有一台master ip是192.168.7.173,和其他集群节点的IP192.168.0.x或192.168.1.x相隔太远,现在需要对网络做整改,方便管理配置诸如绑定限速等操作。 master节点是3节点的。此博客属于事后记…...

c++【入门】已知一个圆的半径,求解该圆的面积和周长?
限制 时间限制 : 1 秒 内存限制 : 128 MB 已知一个圆的半径,求解该圆的面积和周长 输入 输入只有一行,只有1个整数。 输出 输出只有两行,一行面积,一行周长。(保留两位小数)。 令pi3.1415926 样例…...

c#通过sqlsugar查询信息并日期排序
c#通过sqlsugar查询信息并日期字段排序 public static List<Sugar_Get_Info_Class> Get_xml_lot_xx(string lot_number){DBContext<Sugar_Get_Info_Class> db_data DBContext<Sugar_Get_Info_Class>.OpDB();Expression<Func<Sugar_Get_Info_Class, b…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

游戏开发中常见的战斗数值英文缩写对照表
游戏开发中常见的战斗数值英文缩写对照表 基础属性(Basic Attributes) 缩写英文全称中文释义常见使用场景HPHit Points / Health Points生命值角色生存状态MPMana Points / Magic Points魔法值技能释放资源SPStamina Points体力值动作消耗资源APAction…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...


