【TensorFlow深度学习】强化学习中的贝尔曼方程及其应用
强化学习中的贝尔曼方程及其应用
- 强化学习中的贝尔曼方程及其应用:理解与实战演练
- 贝尔曼方程简介
- 应用场景
- 代码实例:使用Python实现贝尔曼方程求解状态价值
- 结语
强化学习中的贝尔曼方程及其应用:理解与实战演练
在强化学习这一复杂而迷人的领域中,贝尔曼方程(Bellman Equation)扮演着核心角色,它是连接过去与未来、理论与实践的桥梁,为智能体的决策优化提供了数学基础。本文将深入探讨贝尔曼方程的原理、其在强化学习算法中的应用,并通过Python代码实例,让你直观感受贝尔曼方程的威力。
贝尔曼方程简介
贝尔曼方程是马尔可夫决策过程(MDP)和部分可观测马尔可夫决策过程(POMDP)中价值函数和Q函数的基础方程。它描述了当前价值如何通过未来的预期回报与即时奖励相结合来更新。简单形式如下:
- 状态价值函数 (V(s)) 的贝尔曼方程:
[ V(s) = \sum_{a} \pi(a|s) \sum_{s’, r} p(s’, r|s, a)[r + \gamma V(s’)] ] - 动作价值函数 (Q(s, a)) 的贝尔曼方程:
[ Q(s, a) = \sum_{s’, r} p(s’, r|s, a)[r + \gamma \max_{a’} Q(s’, a’)] ]
其中,(s) 是当前状态,(a) 是采取的动作,(s’) 是下一状态,(r) 是奖励,(\gamma) 是折现因子,(\pi) 是策略,(p) 是状态转移概率。
应用场景
贝尔曼方程广泛应用于强化学习的各种算法中,包括但不限于:
- 值迭代(Value Iteration) 和 策略迭代(Policy Iteration):通过贝尔曼方程逐步改善策略和价值函数。
- Q-learning 和 SARSA(State-Action-Reward-State-Action):直接更新动作价值函数以学习最优策略。
- Deep Q-Networks (DQN) 和 Actor-Critic 方法:结合神经网络与贝尔曼方程,解决复杂环境问题。
代码实例:使用Python实现贝尔曼方程求解状态价值
假设一个简单的环境,有3个状态,每个状态的转移概率、奖励和一个固定的(\gamma=0.9)。我们将手动计算状态价值函数,演示贝尔曼方程的应用。
import numpy as np# 状态转移矩阵 P(s', r | s, a),简化为示例,只考虑一种动作
P = np.array([[[0.7, 0.2, 0.1, 10], # 状态s1[0.8, 0.1, 0.1, 10], # 状态s2[0.6, 0.3, 0.1, 10]]) # 状态s3
# 奖励矩阵 R(s, a, s')
R = np.array([0, 1, 2, 3]) # 状态转移后奖励
gamma = 0.9 # 折现因子def bellman_equation(V):V_new = np.zeros(3)for s in range(3):for s_prime in range(3):V_new[s] += P[s, s_prime] * (R[s_prime] + gamma * V[s_prime])return V_new# 初始估计值
V_estimated = np.zeros(3)
threshold = 1e-5
while True:V_previous = V_estimated.copy()V_estimated = bellman_equation(V_estimated)if np.max(np.abs(V_estimated - V_previous)) < threshold:breakprint("状态价值函数V(s):", V_estimated)
结语
通过以上实例,我们不仅理解了贝尔曼方程的理论基础,还亲手通过Python代码实现了状态价值函数的迭代计算。贝尔曼方程不仅是强化学习算法的理论基石,更是指导智能体学习如何在未知环境中做出决策的灯塔。随着深度学习的融合,贝尔曼方程在处理高维状态空间和复杂策略优化中展现了前所未有的潜力,开启了智能决策的新纪元。继续探索,你会发现更多贝尔曼方程在强化学习广阔天地中的应用与魅力。
相关文章:

【TensorFlow深度学习】强化学习中的贝尔曼方程及其应用
强化学习中的贝尔曼方程及其应用 强化学习中的贝尔曼方程及其应用:理解与实战演练贝尔曼方程简介应用场景代码实例:使用Python实现贝尔曼方程求解状态价值结语 强化学习中的贝尔曼方程及其应用:理解与实战演练 在强化学习这一复杂而迷人的领…...

牛客 NC129 阶乘末尾0的数量【简单 基础数学 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/aa03dff18376454c9d2e359163bf44b8 https://www.lintcode.com/problem/2 思路 Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改ÿ…...

【Spring Boot】异常处理
异常处理 1.认识异常处理1.1 异常处理的必要性1.2 异常的分类1.3 如何处理异常1.3.1 捕获异常1.3.2 抛出异常1.3.4 自定义异常 1.4 Spring Boot 默认的异常处理 2.使用控制器通知3.自定义错误处理控制器3.1 自定义一个错误的处理控制器3.2 自定义业务异常类3.2.1 自定义异常类3…...

Laravel学习-自定义辅助函数
因为laravel框架的辅助函数helpers不会进入版本库,被版本库忽略的,只有自己创建一个helpers辅助函数。 可以在任意文件下创建helpers.php文件,建议在app目录下, 然后在composer.json文件中,autoload 中间,…...

LLVM Cpu0 新后端6
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...
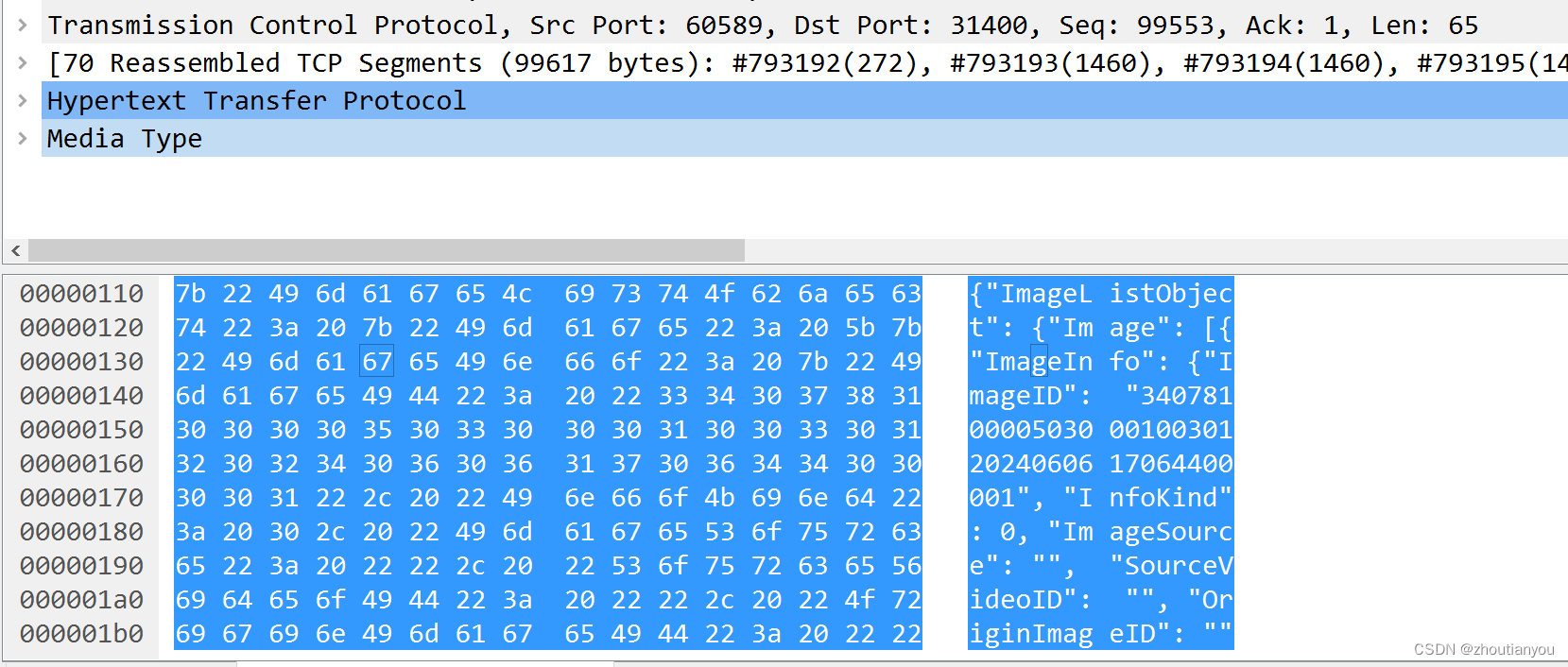
GAT1399协议分析(9)--图像上传
一、官方定义 二、wirechark实例 有前面查询的基础,这个接口相对简单很多。 请求: 文本化: POST /VIID/Images HTTP/1.1 Host: 10.0.201.56:31400 User-Agent: python-requests/2.32.3 Accept-Encoding: gzip, deflate Accept: */* Connection: keep-alive content-type:…...

Spring ApplicationContext的getBean方法
Spring ApplicationContext的getBean方法 在Spring框架的ApplicationContext中,getBean(Class<T> requiredType)方法可以接受一个类类型参数,这个参数可以是接口类也可以是实现类。 使用接口类: 如果requiredType是一个接口,…...
—— 自动摘要)
自然语言处理(NLP)—— 自动摘要
自动摘要是一种将长文本信息浓缩为短文本的技术,旨在保留原文的主要信息和意义。 1 自动摘要的第一种方法 它的第一种方法是基于理解的,受认知科学和人工智能的启发。 在这个方法中,我们首先建立文本的语义表示,这可以理解为文本…...

Spring RestClient报错:400 Bad Request : [no body]
我项目采用微服务架构,所以各服务之间通过Spring RestClient远程调用,本来一直工作得好好的,昨天突然发现远程调用一直报错,错误详情如下: org.springframework.web.client.HttpClientErrorException$BadRequest: 400…...
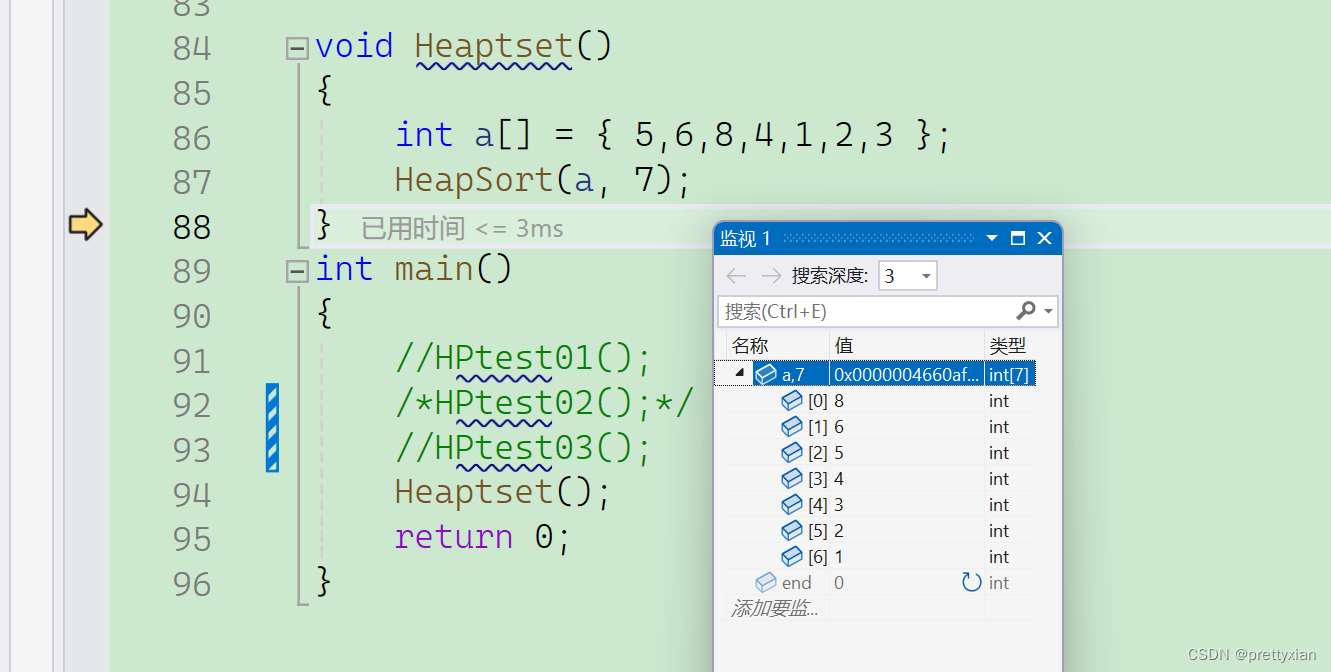
【数据结构】 -- 堆 (堆排序)(TOP-K问题)
引入 要学习堆,首先要先简单的了解一下二叉树,二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。它具有以下特点: 根节点(Root):树的顶部节…...

C#面:XML与 HTML 的主要区别是什么
C# XML与HTML有以下几个主要区别: 用途不同:XML(eXtensible Markup Language)是一种用于存储和传输数据的标记语言,它的主要目的是描述数据的结构和内容。HTML(HyperText Markup Language)是一…...

java并发-如何保证线程按照顺序执行?
【readme】 使用只有单个线程的线程池(最简单)Thread.join() 可重入锁 ReentrantLock Condition 条件变量(多个) ; 原理如下: 任务1执行前在锁1上阻塞;执行完成后在锁2上唤醒;任务…...

PyCharm中 Fitten Code插件的使用说明一
一. 简介 Fitten Code插件是是一款由非十大模型驱动的 AI 编程助手,它可以自动生成代码,提升开发效率,帮您调试 Bug,节省您的时间,另外还可以对话聊天,解决您编程碰到的问题。 前一篇文章学习了 PyCharm…...
Polar Web【简单】PHP反序列化初试
Polar Web【简单】PHP反序列化初试 Contents Polar Web【简单】PHP反序列化初试思路EXP手动脚本PythonGo 运行&总结 思路 启动环境,显示下图中的PHP代码,于是展开分析: 首先发现Easy类中有魔术函数 __wakeup() ,实现的是对成员…...
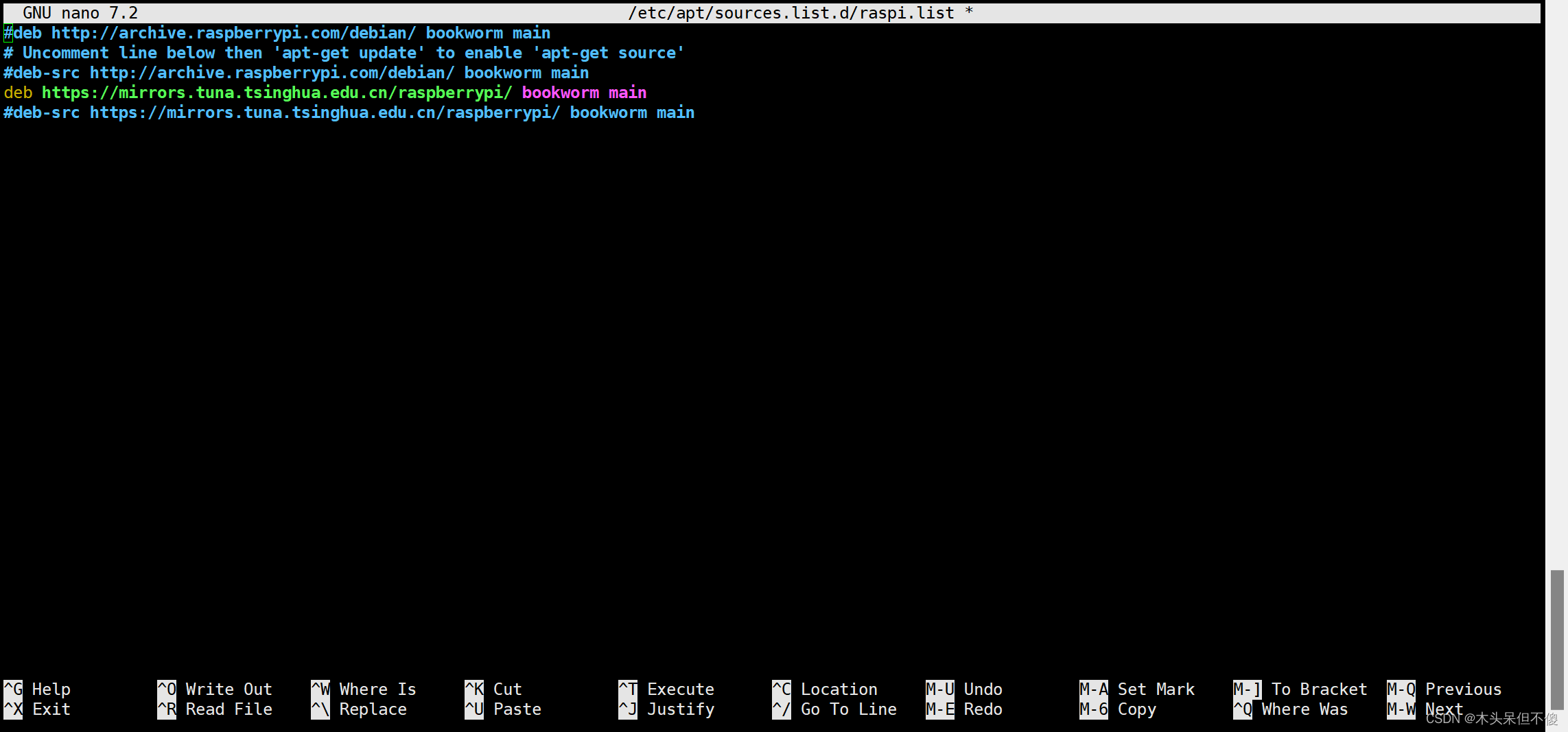
树莓派4B 零起点(二) 树莓派 更换软件源和软件仓库
目录 一、准备工作,查看自己的树莓派版本 二、安装HTTPS支持 三、更换为清华源 1、更换Debian软件源 2,更换Raspberrypi软件仓库 四、进行软件更新 接前章,我们的树莓派已经启动起来了,接下来要干的事那就是更换软件源和软件…...
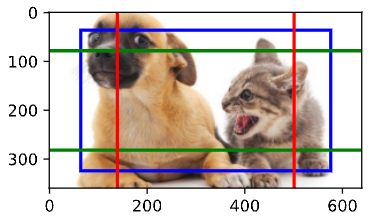
Pytorch 实现目标检测二(Pytorch 24)
一 实例操作目标检测 下面通过一个具体的例子来说明锚框标签。我们已经为加载图像中的狗和猫定义了真实边界框,其中第一个 元素是类别(0代表狗,1代表猫),其余四个元素是左上角和右下角的(x, y)轴坐标(范围…...
进行高效列表操作)
如何使用Python中的列表解析(list comprehension)进行高效列表操作
Python中的列表解析(list comprehension)是一种创建列表的简洁方法,它可以在单行代码中执行复杂的循环和条件逻辑。列表解析提供了一种快速且易于阅读的方式来生成新的列表。 以下是一些使用列表解析进行高效列表操作的示例: 1.…...

java使用websocket遇到的问题
java使用websocket的bug 1 websocket连接正常但是收不到服务端发出的消息java的websocket并发的时候导致连接断开(看着连接是正常的,但是实际上已经断开) 1 websocket连接正常但是收不到服务端发出的消息 java的websocket并发的时候导致连接断…...

[Cloud Networking] Layer 2
文章目录 1. 什么是Mac Address?2. 如何查找MAC地址?3. 二层数据交换4. [Layer 2 Protocol](https://blog.csdn.net/settingsun1225/article/details/139552315) 1. 什么是Mac Address? MAC 地址是计算机的唯一48位硬件编码,嵌入到网卡中。 MAC地址也…...
)
[240609] qwen2 发布,在 Ollama 已可用 | 采用语言模型构建通用 AGI(2020年8月)
目录 qwen2 发布,在 Ollama 已可用Qwen2 模型概览 (基于 Ollama 网站信息)一、模型介绍二、模型参数三、支持语言 (除英语和中文外)四、模型性能五、许可证六、数据支撑: 采用语言模型构建通用 AGI qwen2 发布,在 Ollama 已可用 Qwen2 模型概览 (基于 O…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
