【数据结构】前缀树(字典树)汇总
基础
{“a”,“abc”,“bac”,“bbc”,“ca” }的字典树如下图:

最主用的应用:一,字符串编码。二,位运算。
字符串编码
相比利用哈希映射编码,优点如下:
依次查询长度为n的字符串s的前缀时间复杂度是O(n)。查询完s[0…i],再查询s[0…i+1]的时间复杂度是O(1)。而哈希映射的时间复杂度是:O(nn)。
利用哈希映射编码的代码如下:
注意m_iLeafIndex 为-1,表示此节点不是任何字符串的结束字符。
class CStrToIndex
{
public:CStrToIndex() {}CStrToIndex(const vector<string>& wordList) {for (const auto& str : wordList){Add(str);}}int Add(const string& str){if (m_mIndexs.count(str)) { return m_mIndexs[str]; }m_mIndexs[str] = m_strs.size();m_strs.push_back(str);return m_strs.size()-1;}vector<string> m_strs;int GetIndex(const string& str){if (m_mIndexs.count(str)) { return m_mIndexs[str]; }return -1;}
protected:unordered_map<string, int> m_mIndexs;
};
利用字典树编码的代码如下:
template<class TData = char, int iTypeNum = 26, TData cBegin = 'a'>
class CTrieNode
{
public:~CTrieNode(){for (auto& [tmp, ptr] : m_dataToChilds) {delete ptr;}}CTrieNode* AddChar(TData ele, int& iMaxID){
#ifdef _DEBUGif ((ele < cBegin) || (ele >= cBegin + iTypeNum)){return nullptr;}
#endifconst int index = ele - cBegin;auto ptr = m_dataToChilds[ele - cBegin];if (!ptr){m_dataToChilds[index] = new CTrieNode();
#ifdef _DEBUGm_dataToChilds[index]->m_iID = ++iMaxID;m_childForDebug[ele] = m_dataToChilds[index];
#endif}return m_dataToChilds[index];}CTrieNode* GetChild(TData ele){
#ifdef _DEBUGif ((ele < cBegin) || (ele >= cBegin + iTypeNum)){return nullptr;}
#endifreturn m_dataToChilds[ele - cBegin];}
protected:
#ifdef _DEBUGint m_iID = -1;std::unordered_map<TData, CTrieNode*> m_childForDebug;
#endif
public:int m_iLeafIndex = -1;
protected://CTrieNode* m_dataToChilds[iTypeNum] = { nullptr };//空间换时间 大约216字节//unordered_map<int, CTrieNode*> m_dataToChilds;//时间换空间 大约56字节map<int, CTrieNode*> m_dataToChilds;//时间换空间,空间略优于哈希映射,数量小于256时,时间也优。大约48字节
};
template<class TData = char, int iTypeNum = 26, TData cBegin = 'a'>
class CTrie
{
public:int GetLeadCount(){return m_iLeafCount;}CTrieNode<TData, iTypeNum, cBegin>* AddA(CTrieNode<TData, iTypeNum, cBegin>* par,TData curValue){auto curNode =par->AddChar(curValue, m_iMaxID);FreshLeafIndex(curNode);return curNode;}template<class IT>int Add(IT begin, IT end){auto pNode = &m_root;for (; begin != end; ++begin){pNode = pNode->AddChar(*begin, m_iMaxID);}FreshLeafIndex(pNode);return pNode->m_iLeafIndex;} template<class IT>CTrieNode<TData, iTypeNum, cBegin>* Search(IT begin, IT end){auto ptr = &m_root;for (; begin != end; ++begin){ptr = ptr->GetChild(*begin);if (nullptr == ptr){return nullptr;}}return ptr;}CTrieNode<TData, iTypeNum, cBegin> m_root;
protected:void FreshLeafIndex(CTrieNode<TData, iTypeNum, cBegin>* pNode){if (-1 == pNode->m_iLeafIndex){pNode->m_iLeafIndex = m_iLeafCount++;}}int m_iMaxID = 0;int m_iLeafCount = 0;
};
二进制位运算(01前缀树)
比如求nums和x的xor最大值。
将nums放到01放到前缀树中。通过拆位法依次从高到低处理各位,如果x 此为1,则优先选择前缀树的0分支;如果x为0,则优先选择前缀树的1分支。
class C2BNumTrieNode
{
public:C2BNumTrieNode(){m_childs[0] = m_childs[1] = nullptr;}bool GetNot0Child(bool bFirstRight){auto ptr = m_childs[bFirstRight];if (ptr && (ptr->m_iNum > 0)){return bFirstRight;}return !bFirstRight;}int m_iNum = 0;C2BNumTrieNode* m_childs[2];
};template<class T = int, int iLeveCount = 31>
class C2BNumTrie
{
public:C2BNumTrie(){m_pRoot = new C2BNumTrieNode();}void Add(T iNum){m_setHas.emplace(iNum);C2BNumTrieNode* p = m_pRoot;for (int i = iLeveCount - 1; i >= 0; i--){p->m_iNum++;bool bRight = iNum & ((T)1 << i);if (nullptr == p->m_childs[bRight]){p->m_childs[bRight] = new C2BNumTrieNode();}p = p->m_childs[bRight];}p->m_iNum++;}void Del(T iNum){auto it = m_setHas.find(iNum);if (m_setHas.end() == it){return;}m_setHas.erase(it);C2BNumTrieNode* p = m_pRoot;for (int i = iLeveCount - 1; i >= 0; i--){p->m_iNum--;bool bRight = iNum & ((T)1 << i);p = p->m_childs[bRight];}p->m_iNum--;} void Swap(C2BNumTrie<T, iLeveCount>& o) {swap(m_pRoot, o.m_pRoot);swap(m_setHas, o.m_setHas);}C2BNumTrieNode* m_pRoot;std::unordered_multiset<T> m_setHas;
};template<class T = int, int iLeveCount = 31>
class CMaxXor2BTrie : public C2BNumTrie<T, iLeveCount>
{
public:T MaxXor(T iNum){C2BNumTrieNode* p = C2BNumTrie<T, iLeveCount>::m_pRoot;T iRet = 0;for (int i = iLeveCount - 1; i >= 0; i--){bool bRight = !(iNum & ((T)1 << i));bool bSel = p->GetNot0Child(bRight);p = p->m_childs[bSel];if (bSel == bRight){iRet |= ((T)1 << i);}}return iRet;}
};
题解
| 给字符串编码 | 难道分 |
|---|---|
| 字典树】 【哈希表】 【字符串】3076. 数组中的最短非公共子字符串 | 1635 |
| 【字典树(前缀树) 字符串】2416. 字符串的前缀分数和需要记录子孙数量 | 1725 |
| 【字典树 最长公共前缀】1316. 不同的循环子字符串 | 1836 |
| 【字典树(前缀树)】1032. 字符流 | 1970 |
| 【map】【滑动窗口】【字典树】C++算法:2781最长合法子字符串的长度 | 2203 |
| 【字典树】【字符串】【 前缀】3093. 最长公共后缀查询 | 2118 |
| 【字典树】【KMP】【C++算法】3045统计前后缀下标对 II | 2327 |
| 【字典树 离线查询 深度优先】1938. 查询最大基因差 | 2502 |
| 动态规划 多源路径 字典树 LeetCode2977:转换字符串的最小成本 | 2695 |
| 【动态规划】 【字典树】C++算法:472 连接词 | |
| 【回溯 字典树(前缀树)】212. 单词搜索 II | |
| 【字典树 马拉车算法】336. 回文对 |
| 01前缀树 | |
|---|---|
| 【字典树】2935找出强数对的最大异或值 II | 2348 |
| 【字典树(前缀树) 异或 离线查询】1707. 与数组中元素的最大异或值 | 2358 |
| 【字典树(前缀树) 位运算】1803. 统计异或值在范围内的数对有多少 | 2479 |
| 其它前缀树 | |
|---|---|
| 【字典树(前缀树) 哈希映射 后序序列化】1948. 删除系统中的重复文件夹需要DFS | 2533 |

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 《喜缺全书算法册》以原理、正确性证明、总结为主。 |
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【数据结构】前缀树(字典树)汇总
基础 {“a”,“abc”,“bac”,“bbc”,“ca” }的字典树如下图: 最主用的应用:一,字符串编码。二,位运算。 字符串编码 相比利用哈希映射编码,优点如下: 依次查询长度为n的字符串s的前缀时间复杂度是O(…...
Linux:基础开发工具
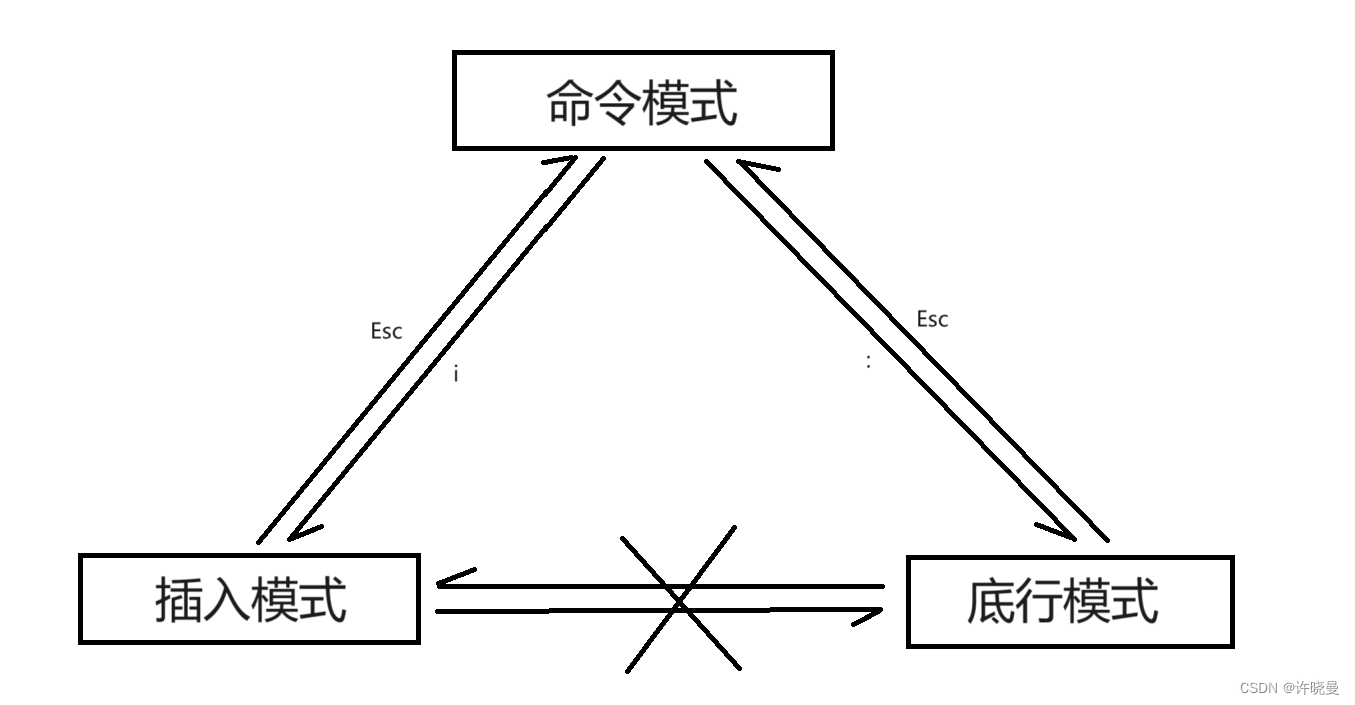
文章目录 Linux 软件包管理器 yum什么是软件包关于rzsz查看软件包安装软件卸载软件安装扩展源 Linux 编辑器 vimvim的基本概念正常/普通/命令模式(Normal mode)插入模式(Insert mode)底行模式(last line mode) vim的基本操作[命令模式]切换至[插入模式][插入模式]切换至[命令模…...

HarmonyOS NEXT Push接入
接入HarmonyOS NEXT Push 推送功能,相比于 Android 真的是简单太多。不再需要适配接入各个厂家的推送 SDK,真是舒服。 1.开通推送服务与配置Client ID 1.1 创建应用获取Client ID 按照官方文档来就可以了:https://developer.huawei.com/co…...

如何快速入门Element-UI:打造高效美观的前端界面
Element-UI 是一款基于 Vue.js 的开源组件库,提供了丰富的 UI 组件,可以帮助开发者快速构建美观、响应式的前端界面。本文将详细介绍如何快速入门 Element-UI,包括环境搭建、组件使用、样式定制及常见问题解决方法,帮助你高效地使用 Element-UI 进行前端开发。 一、环境搭…...

Langchain的向量存储 - Document示例代码里的疑问
文章目录 前言一、语句分析二、 举例解释三、 完整代码总结 前言 之前的代码里有下面这句话,可能有看不明白的读者。 vectors [embeddings.embed(doc.page_content) for doc in docs]今天一起来看下这句话。 一、语句分析 这句话实际上是一个列表推导式&#x…...

Docker 教程-介绍-2
快速了解docker有什么。 Docker简介 Docker 是一个开源的应用容器引擎,基于Go语言开发,并遵循Apache 2.0协议。它允许开发者将应用及其依赖包打包进一个可移植的容器中,这些容器可以发布到任何支持Docker的Linux或Windows机器上,…...
 - 三语言AC题解(Python/Java/Cpp))
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 伐木工(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 伐木工(200分) 🌍 评测功能需要订阅专栏后私信联系清隆解…...

UltraScale+系列模块化仪器,可以同时用作控制器、算法加速器和高速数字信号处理器
基于 XCZU7EG / XCZU4EG / XCZU2EG • 灵活的模块组合 • 易于嵌入的紧凑型外观结构 • 高性能的 ARM Cortex 处理器 • 成熟的 FPGA 可编程逻辑 ,基于 IP 核的软件库 基于 Xilinx Zynq UltraScaleMPSoC 的 FPGA 技术,采用 Xilinx Zynq UltraScale&a…...
相比有哪些优势?)
Python与其他编程语言(如Java、C++)相比有哪些优势?
一、技术难点 在探讨Python与其他编程语言相比的优势时,技术难点在于如何全面、准确地把握并阐述这些优势。这需要对Python、Java、C等编程语言有深入的理解,包括它们的语法特性、应用领域、性能特点、开发效率等。 首先,Python的语法简洁明…...

Edge浏览器双击关闭标签页,双击关闭浏览器选项卡
设置》外观》自定义浏览器,开启“使用双击关闭浏览器选项卡” 设置里面搜索“双击”,这是最快的方式 鼠标滚轮单击 或者进入“设置”-“辅助功能” 呼吁已久的功能来了!Edge浏览器双击关闭标签页功能上线新 国产浏览器大多都有双击关闭标签页…...

C++ 贪心算法——跳跃游戏、划分字母区间
一:跳跃游戏 55. 跳跃游戏 题目描述:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回 true ࿱…...

汽车数据应用构想(三)
上期说的,用数据去拟合停车信息的应用,那么类似的POI信息相关的场景其实都可以实现。今天讲讲用户使用频率也很高的加油/充电场景。 实际应用中,在加油场景中用户关心的通常还是价格。无论是导航还是各种加油APP/小程序,都已经很…...

体素技术在AI绘画中的革新作用
随着人工智能技术的不断进步,AI绘画已经成为艺术创作和视觉设计领域的一大趋势。在众多推动AI绘画发展的技术中,体素技术以其独特的优势,正在逐渐改变着我们对计算机生成图像的认识。本文旨在探讨体素技术在AI绘画中的应用与影响,…...

Leetcode.866 回文质数
题目链接 Leetcode.866 回文质数 rating : 1938 题目描述 给你一个整数 n n n ,返回大于或等于 n n n 的最小 回文质数。 一个整数如果恰好有两个除数: 1 1 1 和它本身,那么它是 质数 。注意, 1 1 1 不是质数。 例如…...
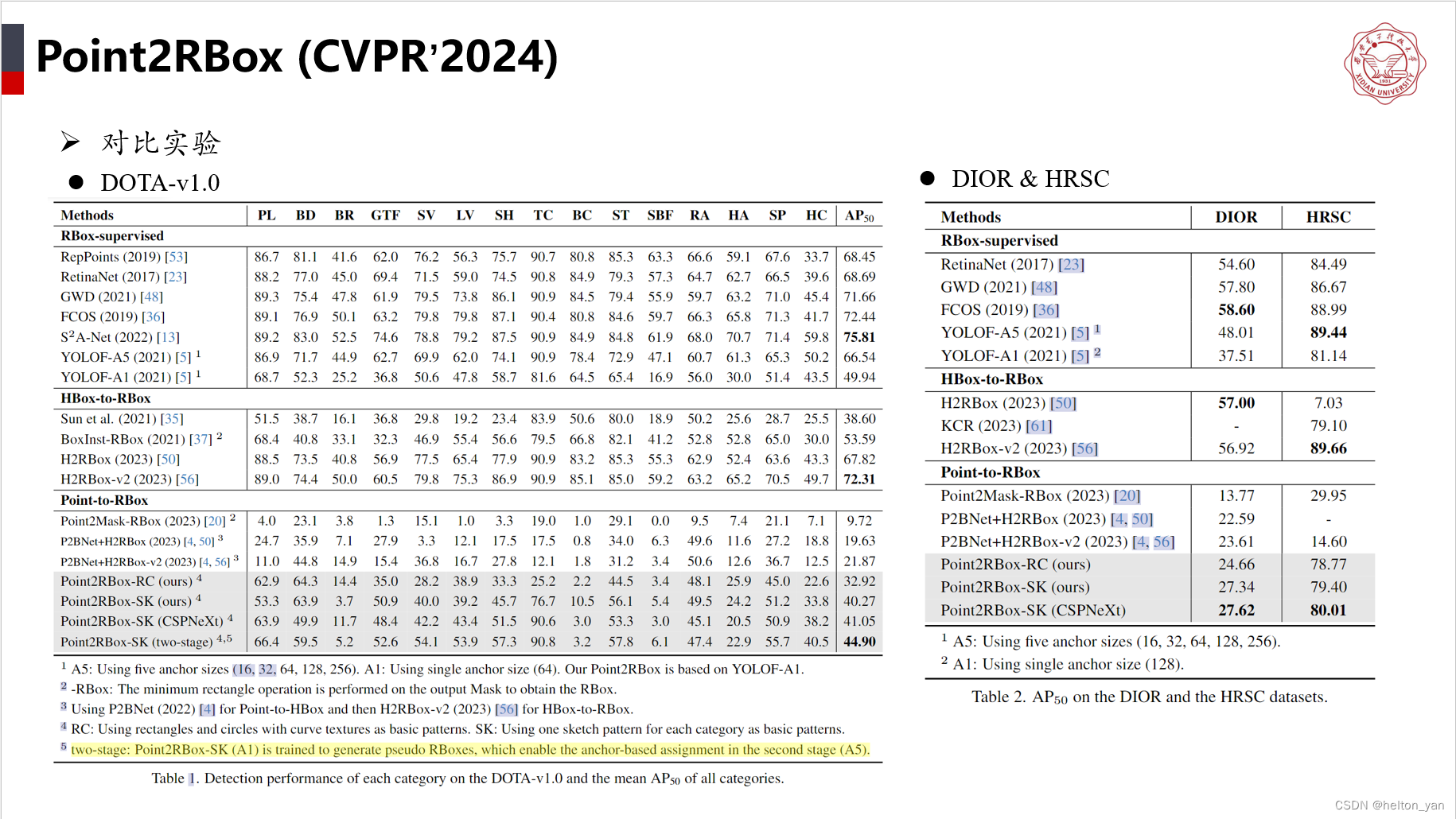
【论文阅读】Point2RBox (CVPR’2024)
paper:https://arxiv.org/abs/2311.14758 code:https://github.com/yuyi1005/point2rbox-mmrotate...

深度学习的点云分割
深度学习的点云分割 点云分割是计算机视觉中的一个重要任务,特别是在三维数据处理和分析中。点云数据是由大量三维点构成的集合,每个点包含空间坐标(x, y, z),有时还包含其他信息如颜色和法向量。点云分割的目标是将点…...

【知识点】c++模板特化
在 C 中,模板特化分为全特化(full specialization)和偏特化(partial specialization)。它们允许程序员为特定类型或类型模式提供不同的实现,以覆盖通用模板的默认行为。 模板全特化 模板全特化是指为某个…...

算法家族之一——二分法
目录 算法算法的打印效果如果算法里的整型“i”为1如果算法里的整型“i”为11 算法的流程图算法的实际应用总结 大家好,我叫 这是我58,现在,请看下面的算法。 算法 #define _CRT_SECURE_NO_WARNINGS 1//<--预处理指令 #include <stdi…...
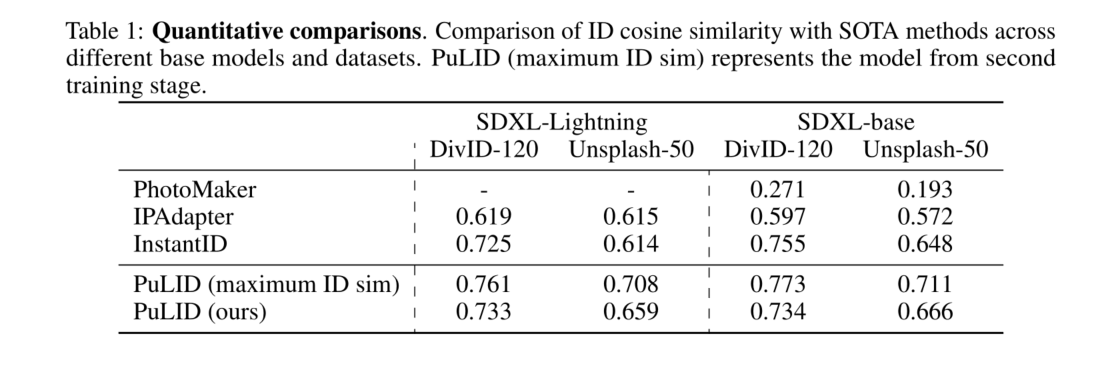
【深度学习】PuLID: Pure and Lightning ID Customization via Contrastive Alignment
论文:https://arxiv.org/abs/2404.16022 代码:https://github.com/ToTheBeginning/PuLID 文章目录 AbstractIntroductionRelated WorkMethods Abstract 我们提出了一种新颖的、无需调整的文本生成图像ID定制方法——Pure and Lightning ID customizatio…...

Elastic 8.14:用于简化分析的 Elasticsearch 查询语言 (ES|QL) 正式发布
作者:来自 Elastic Brian Bergholm 今天,我们很高兴地宣布 Elastic 8.14 正式发布。 什么是新的? 8.14 版本最重要的标题是 ES|QL 的正式发布(GA),它是从头开始设计和专门构建的,可大大简化数据调查。在新的查询引擎的…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
