当前位置： 首页 > news >正文

centos学习记录

news 2026/2/8 10:14:15

遇到的问题及其解决办法

centos7安装图形化界面

yum groupinstall ‘X Window System’
yum groupinstall -y ‘GNOME Desktop’
安装完成后输入init 5进入图形化界面

centos7安装vmware-tools
第一步卸载open-vm-tools
输入命令 yum remove open-vm-tools
输入命令 reboot
在VMware当中选择虚拟机->安装Vmware Tools
centos7桌面会显示VMware-tools光盘
进入光盘终端后
输入如下命令

cp VMwareTools-10.3.23-16594550.tar.gz /root
chmod +x VMwareTools-10.3.23-16594550.tar.gz 
tar zxpf VMwareTools-10.3.23-16594550.tar.gz
cd vmware-tools-distrib
./vmware-install.pl

执行过程中遇到停顿按回车，安装好了之后重新安装open-vm-tools-desktop
输入如下命令 yum instal open-vm-tools-desktop，重启机器，reboot，完成

解决输入中文的问题
终端输入命令 yum install ibus-libpinyin
把区域和语言(Region & Language)中的输入源换成汉语)Intelligent Pinyin)
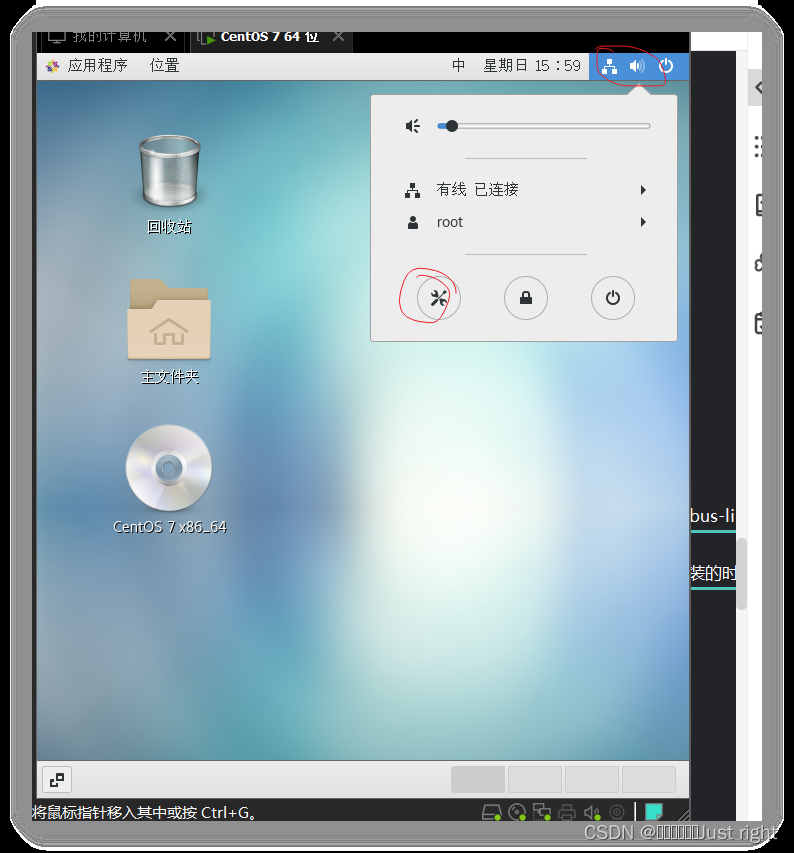
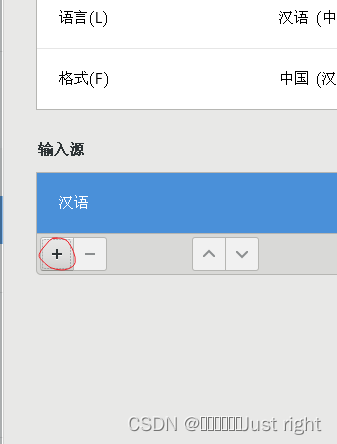
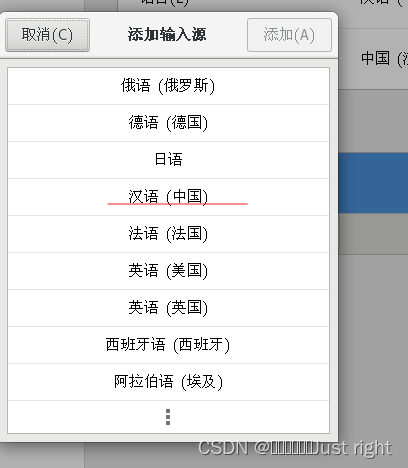
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

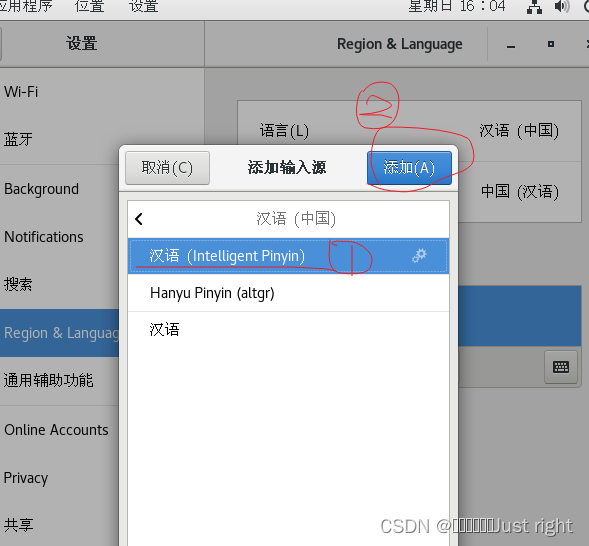
win + 空格 切换输入法
完成

报错记录及其解决办法

报错记录
报错提示: No package ifconfig available Error:Nothing to do
解决办法: yum install net-tools.x86_64 -y

相关文章：

centos学习记录

遇到的问题及其解决办法 centos7安装图形化界面 yum groupinstall ‘X Window System’ yum groupinstall -y ‘GNOME Desktop’ 安装完成后输入init 5进入图形化界面 centos7安装vmware-tools 第一步卸载open-vm-tools 输入命令 yum remove open-vm-tools 输入命令 reboot 在…...

编程日记 2023/2/12 19:47:32

为什么说网络安全是风口行业？

前言 “没有网络安全就没有国家安全”。当前，网络安全已被提升到国家战略的高度，成为影响国家安全、社会稳定至关重要的因素之一。 网络安全行业特点 1、就业薪资非常高，涨薪快 2021年猎聘网发布网络安全行业就业薪资行业最高人均33.77万&…...

编程日记 2023/2/12 19:46:22

12-PHP使用过的函数 111-120

111、rowCount if ($stmt->execute($data)) {//true//读:select//写:insert,update,delete,成功后会返回表中受影响的记录数量//!rowCount() 返回受影响的记录数量if ($stmt->rowCount() > 0) {echo 新增成功,id . $db->lastInsertId() . <hr>;} else {//…...

编程日记 2023/2/12 19:45:16

【JavaWeb项目】简单搭建一个前端的博客系统

博客系统项目 本项目主要分成四个页面: 博客列表页博客详情页登录页面博客编辑页 该系统公共的CSS样式 common.css /* 放置一些各个页面都会用到的公共样式 */* {margin: 0;padding: 0;box-sizing: 0; }/* 给整个页面加上背景 */ html, body{height: 100%; }body {backgrou…...

编程日记 2023/2/12 19:43:59

iPerf3 -M参数详解，场景分析

本文目录iPerf3 -M参数说明几个典型测试场景中应该如何设定合适的-M参数值理想局域网模型&#xff08;无丢包&#xff0c;无抖动&#xff09;高丢包&#xff0c;无抖动模型高丢包&#xff0c;高抖动模型&#xff08;网络质量比较差&#xff0c;IP转发路径变化频繁&#xff09;总…...

编程日记 2023/2/12 19:42:53

java的基本语法以及注意事项

Java 基础语法一个 Java 程序可以认为是一系列对象的集合&#xff0c;而这些对象通过调用彼此的方法来协同工作。下面简要介绍下类、对象、方法和实例变量的概念。对象&#xff1a;对象是类的一个实例&#xff0c;有状态和行为。例如&#xff0c;一条狗是一个对象&#xff0c;它…...

编程日记 2023/2/12 19:41:41

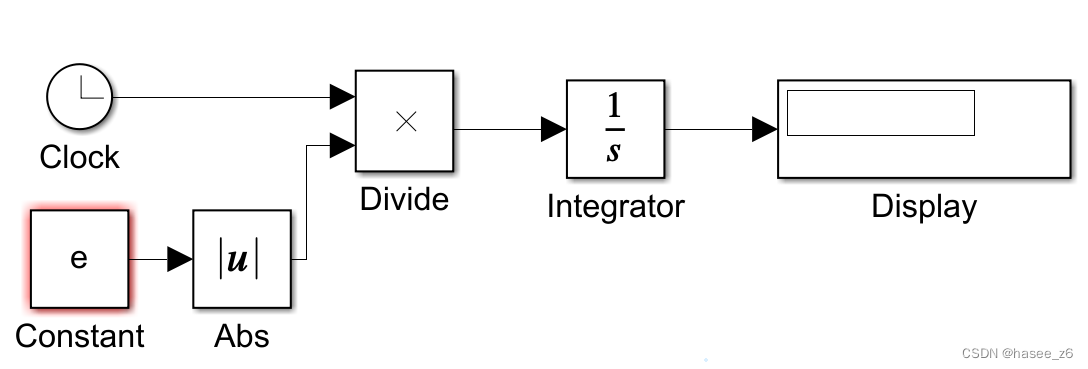
matlab搭建IAE，ISE，ITAE性能指标

目录前言准备IAEISEITAE前言 最近在使用matlab搭建控制系统性能评价指标模型&#xff0c;记录一下 准备 MATLAB R2020 IAE IAE函数表达式如下所示&#xff1a; IAE函数模型如下所示&#xff1a; ISE ISE函数表达式如下所示&#xff1a; ISE函数模型如下所示&#xff…...

编程日记 2023/2/12 19:40:36

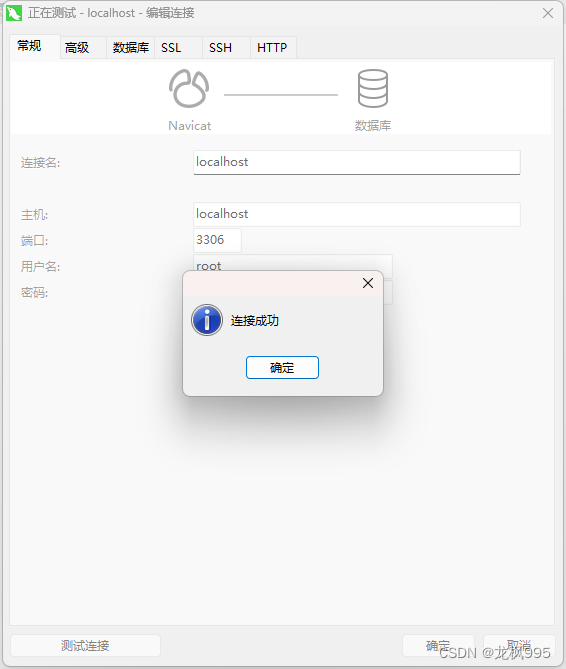
docker安装mysql

在安装Mysql之前&#xff0c;我们可以先查看一下我们的镜像&#xff0c;输入命令&#xff1a; docker images 能发现&#xff0c;镜像里面只有一个Nginx&#xff0c;并没有Mysql 然后我们可以像上一篇安装Nginx一样&#xff0c;安装Mysql镜像。 输入以下命令&#xff0c;安装…...

编程日记 2023/2/12 19:39:28

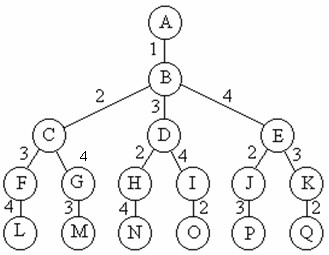
Leetcode 回溯详解

回溯法 回溯法有“通用解题法”之称&#xff0c;用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。 在包含问题的所有解的解空间树中&#xff0c;按照深度优先搜索(DFS)&#xff09;的策略&#xff0c;从根结点出发深度探索解空间树。当探索…...

编程日记 2023/2/12 19:38:19

AI_Papers：第一期

2023.02.06—2023.02.12 文摘词云 Top Papers Subjects: cs.CL 1.Multimodal Chain-of-Thought Reasoning in Language Models 标题&#xff1a;语言模型中的多模式思维链推理 作者&#xff1a;Zhuosheng Zhang, Aston Zhang, Mu Li, Hai Zhao, George Karypis, Alex Sm…...

编程日记 2023/2/12 19:37:13

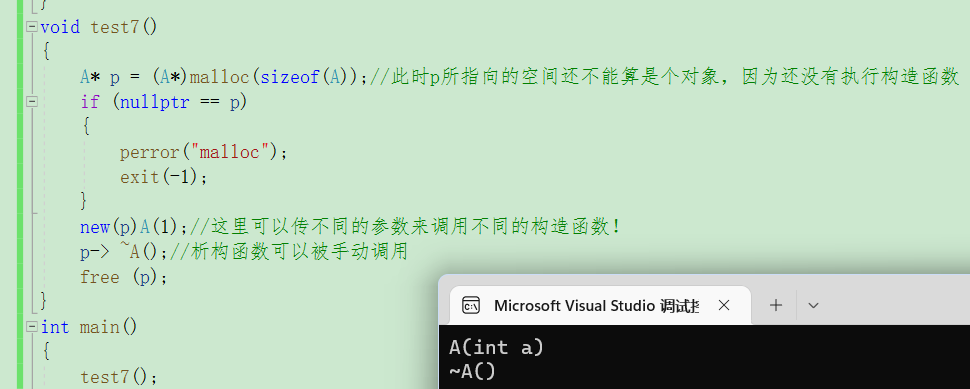
C/C++内存管理

C/C内存管理C/C内存分布C语言中内存管理的方式&#xff1a;malloc/calloc/realloc/freeC内存管理方式内置类型自定义类型operator new 与operator deletenew和delete的实现原理内置类型自定义类型定位new表达式(placement-new)new/delete与malloc/free的区别C/C内存分布 我们先…...

编程日记 2023/2/12 19:36:06

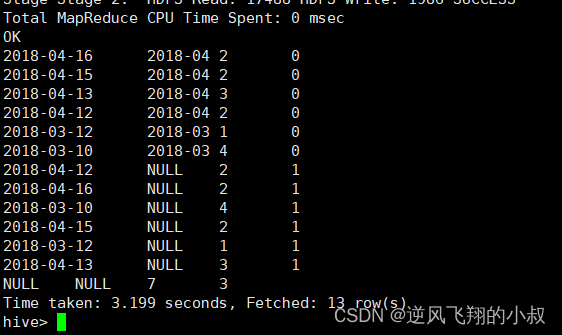
【大数据hive】hive 函数使用详解

一、前言 在任何一种编程语言中&#xff0c;函数可以说是必不可少的&#xff0c;像mysql、oracle中&#xff0c;提供了很多内置函数&#xff0c;或者通过自定义函数的方式进行定制化使用&#xff0c;而hive作为一门数据分析软件&#xff0c;随着版本的不断更新迭代&#xff0c…...

编程日记 2023/2/12 19:34:58

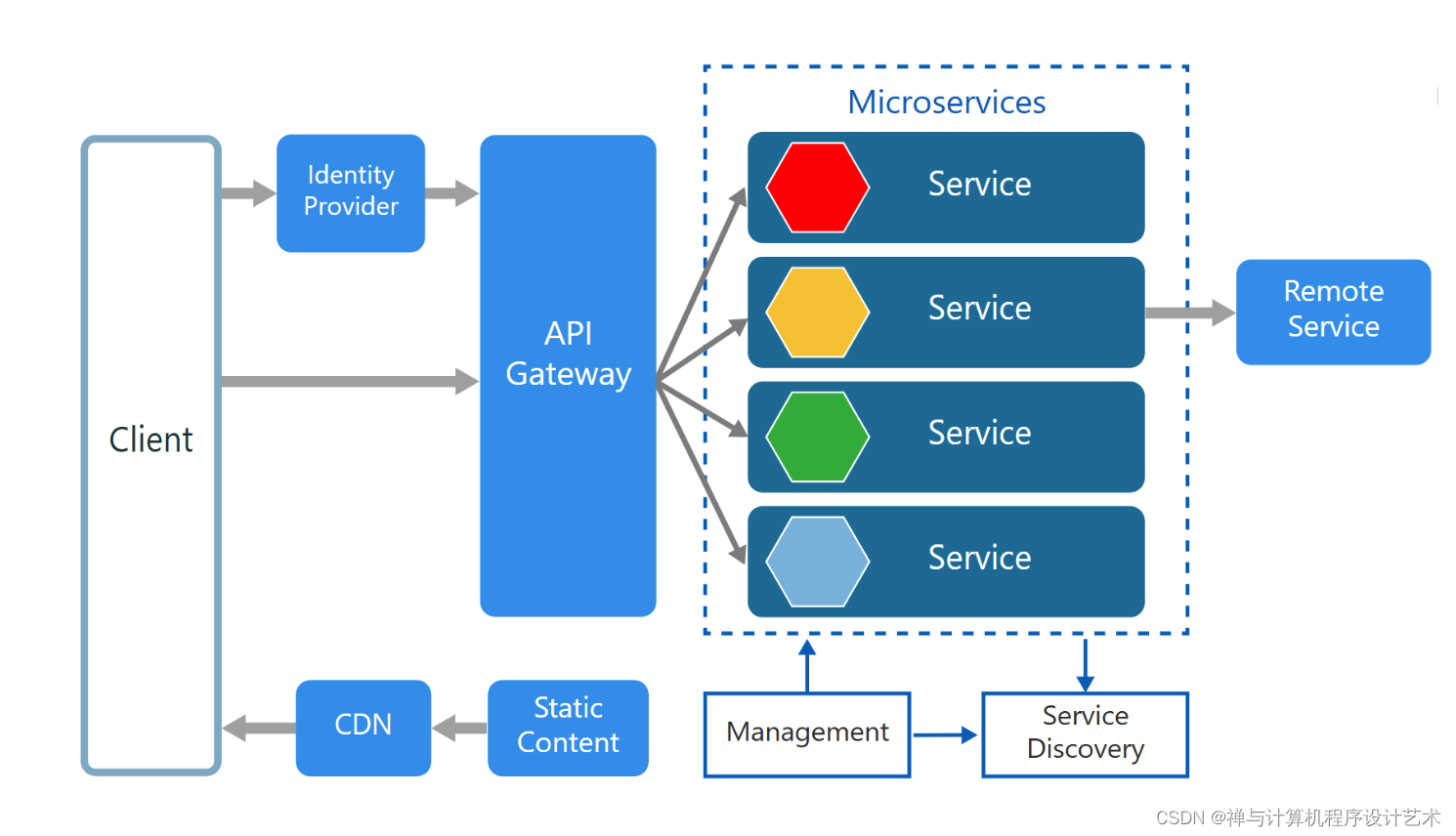
彻底搞懂分布式系统服务注册与发现原理

目录 引入服务注册与发现组件的原因 单体架构 应用与数据分离...

编程日记 2023/2/12 19:32:47

安卓Camera2用ImageReader获取NV21源码分析

以前如何得到Camera预览流回调 可以通过如下方法&#xff0c;得到一路预览回调流 Camera#setPreviewCallbackWithBuffer(Camera.PreviewCallback)&#xff0c;可以通过如下方法&#xff0c;设置回调数据的格式&#xff0c;比如 ImageFormat.NV21 Camera.Parameters#setPreview…...

编程日记 2023/2/12 19:31:39

24. 两两交换链表中的节点

文章目录题目描述迭代法递归法参考文献题目描述 给你一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题&#xff08;即&#xff0c;只能进行节点交换&#xff09;。 示例 1&#xff1a; 输入&a…...

编程日记 2023/2/12 19:30:30

linux006之帮助命令

linux帮助命令简介&#xff1a; linux的命令是非常多的&#xff0c;光靠人是记不住的&#xff0c;在工作中一般都会去网上查&#xff0c;这是有外网的情况下&#xff0c;如果项目中不允许访问外网&#xff0c;那么linux的帮助命令就可以派上用场了&#xff0c; linux帮助命令是…...

编程日记 2023/2/12 19:29:22

【C++初阶】十三、模板进阶（总）|非类型模板参数|模板的特化|模板分离编译|模板总结（优缺点）

目录 一、非类型模板参数 二、模板的特化 2.1 模板特化概念 2.2 函数模板特化 2.3 类模板特化 2.3.1 全特化 2.3.2 偏特化 三、模板分离编译 四、模板总结&#xff08;优缺点&#xff09; 前言&#xff1a;之前模板初阶并没有把 C模板讲完&#xff0c;因为当时没有接触…...

编程日记 2023/2/12 19:28:14

Linux之文本搜索命令

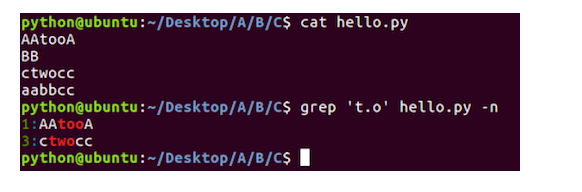
文本搜索命令学习目标能够知道文本搜索使用的命令1. grep命令的使用命令说明grep文本搜索grep命令效果图:2. grep命令选项的使用命令选项说明-i忽略大小写-n显示匹配行号-v显示不包含匹配文本的所有行-i命令选项效果图:-n命令选项效果图:-v命令选项效果图:3. grep命令结合正则表…...

编程日记 2023/2/12 19:27:05

微信小程序Springboot 校园拼车自助服务系统java

系统管理员&#xff1a; 管理员账户管理&#xff1a;在线对管理员的账户信息进行管理&#xff0c;包括对管理员信息的增加修改以及密码的修改等。 站内新闻管理&#xff1a;在后台对站内新闻信息进行发布&#xff0c;并能够对站内新闻信息进行删除修改等。 论坛版块管理&#x…...

编程日记 2023/2/12 19:25:50

【Unity3D 常用插件】Haste插件

一&#xff0c;Haste介绍 Haste插件是一款针对 Unity 3D 的 Everthing软件&#xff0c;可以实现基于名称快速定位对象的功能。Unity 3D 编辑器也自带了搜索功能&#xff0c;但是在 project视图 和 Hierarchy视图 中的对象需要分别查找&#xff0c;不支持模糊匹配。Haste插件就…...

编程日记 2023/2/12 19:24:42

【kafka】Golang实现分布式Masscan任务调度系统

要求&#xff1a; 输出两个程序&#xff0c;一个命令行程序&#xff08;命令行参数用flag&#xff09;和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽&#xff0c;然后将消息推送到kafka里面。 服务端程序&#xff1a; 从kafka消费者接收…...

编程新知 2026/2/4 19:38:41

K8S认证|CKS题库+答案| 11. AppArmor

目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作&#xff1a; 1&#xff09;、切换集群 2&#xff09;、切换节点 3&#xff09;、切换到 apparmor 的目录 4&#xff09;、执行 apparmor 策略模块 5&#xff09;、修改 pod 文件 6&#xff09;、…...

编程新知 2026/1/29 2:11:35

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达

先前我们总结了浏览器选区模型的交互策略&#xff0c;并且实现了基本的选区操作&#xff0c;还调研了自绘选区的实现。那么相对的&#xff0c;我们还需要设计编辑器的选区表达&#xff0c;也可以称为模型选区。编辑器中应用变更时的操作范围&#xff0c;就是以模型选区为基准来…...

编程新知 2026/1/16 16:34:26

使用分级同态加密防御梯度泄漏

抽象 联邦学习 &#xff08;FL&#xff09; 支持跨分布式客户端进行协作模型训练&#xff0c;而无需共享原始数据&#xff0c;这使其成为在互联和自动驾驶汽车 &#xff08;CAV&#xff09; 等领域保护隐私的机器学习的一种很有前途的方法。然而&#xff0c;最近的研究表明&…...

编程新知 2026/1/24 6:22:43

pam_env.so模块配置解析

在PAM&#xff08;Pluggable Authentication Modules&#xff09;配置中&#xff0c; /etc/pam.d/su 文件相关配置含义如下&#xff1a; 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块&#xff0c;负责验证用户身份&am…...

编程新知 2025/10/5 8:09:39

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例

文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...

编程新知 2026/1/26 9:48:34

C++ 基础特性深度解析

目录 引言 一、命名空间&#xff08;namespace&#xff09; C 中的命名空间​ 与 C 语言的对比​ 二、缺省参数​ C 中的缺省参数​ 与 C 语言的对比​ 三、引用&#xff08;reference&#xff09;​ C 中的引用​ 与 C 语言的对比​ 四、inline&#xff08;内联函数…...

编程新知 2026/1/15 4:25:16

C++中string流知识详解和示例

一、概览与类体系 C 提供三种基于内存字符串的流&#xff0c;定义在 <sstream> 中&#xff1a; std::istringstream&#xff1a;输入流&#xff0c;从已有字符串中读取并解析。std::ostringstream&#xff1a;输出流&#xff0c;向内部缓冲区写入内容&#xff0c;最终取…...

编程新知 2025/11/30 11:30:47

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2026/2/6 2:05:50

关键领域软件测试的突围之路：如何破解安全与效率的平衡难题

在数字化浪潮席卷全球的今天&#xff0c;软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件&#xff0c;这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下&#xff0c;实现高效测试与快速迭代&#xff1f;这一命题正考验着…...

编程新知 2026/1/27 13:20:11