Codeforces Round 952 (Div. 4) c++题解(A-H1)
开头 :
这场没打,今天vp了一下,写了A-G,然后就去吃饭了!
比赛链接 :
Dashboard - Codeforces Round 952 (Div. 4) - Codeforces
A
直接交换,输出即可
inline void solve(){string a , b ; cin >> a>> b ;char c = a[0] ;a[0] = b[0] ;b[0] = c ;cout << a << " " << b << endl ;
}B
数据范围小,模拟那个过程即可;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
typedef long long LL;
typedef unsigned long long ULL ;
#define PI acos(-1)
#define endl '\n'
#define pair<int,int> PII ;
#define x first
#define y second
#define no do { cout << "No" << endl; return; } while(0)
#define yes do { cout << "Yes" << endl; return; } while (0)
#define lowbit(x) ((x) & -(x))
#define rep(i, s, e) for (int i=(s);i<(e);++i)
#define all(v) v.begin(), v.end()
#define pb push_back
const LL INF = 1e18 ;
const int mod = 1e9+7;
const int N = 2e5+10;
int dx[4] = {0, 1, 0, -1}, dy[5] = {1, 0, -1, 0};LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;
}LL qmi(int m, int k, int p){int res = 1 % p, t = m;while (k){if (k&1) res = res * t % p;t = t * t % p;k >>= 1;}return res;}inline void solve(){int n ; cin >> n ;int ans = 0 ,yss = 1 ;rep(i,2,n+1){int x = i ;int res = 0 ;while(x<=n){res += x ;x += i ;}if(res>ans) {ans = res ;yss = i ;}}cout << yss << endl ;
}signed main(){IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}C
也是模拟遍历,先用前缀和预处理一下;
如果ma * 2 = b[i],表示a[1,i]是满足题目条件的;
inline void solve(){int n ; cin >> n ;rep(i,1,n) cin >> a[i] ;rep(i,1,n) b[i] = b[i-1] + a[i] ;int ans = 0 ;// ma // b[i]-ma = maLL ma = 0 ;rep(i,1,n){ma = max(ma,a[i]) ;if(ma*2==b[i]) ans ++ ;}cout << ans << endl;
}D
因为所有点都是关于中心点对称分布的,直接求横坐标,纵坐标的平均数就是答案了
inline void solve(){int n ,m ; cin >> n >> m ;vector<vector<char>> a(n+1,vector<char>(m+1)) ;vector<PII> b ;rep(i,1,n)rep(j,1,m){cin >> a[i][j] ;if(a[i][j]=='#') b.pb({i,j}) ;}int sz = b.size() ;int xx , yy ;if(sz==1){xx = b[0].x ; yy = b[0].y ;cout << xx << " " << yy << endl ;return ;}LL xs = 0 , ys = 0 ; for(auto& bc : b){int xc = bc.x , yc = bc.y ;xs += xc ;ys += yc ; }xx = xs / sz ;yy = ys / sz ;cout << xx << " " << yy << endl ;
}E
直接暴力即可,遍历其中两条边,复杂度(2000^2) ;
对于每个满足条件的长宽高i,j,k(也就是i*j*k==s),在S中的移动范围分别是[i,x],[j,y],[k,z];
然后相乘即可;
inline void solve(){LL x , y , z , s ; cin >> x >> y >> z >> s ;LL ans = 0 ;rpL(i,1,x){rpL(j,1,y){LL k = s / (i*j) ;if(s%(i*j)==0 && k<=z){LL res = (x-i+1)*(y-j+1)*(z-k+1) ;ans = max(ans,res) ;}}}cout << ans << endl;
}F
一个非常明显的二分答案,但是用堆也可以做;
(可能这场题多的原因);
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
typedef long long LL;
typedef unsigned long long ULL ;
#define PI acos(-1)
#define endl '\n'
#define PII pair<int,int>
#define x first
#define y second
#define no do { cout << "No" << endl; return; } while(0)
#define yes do { cout << "Yes" << endl; return; } while (0)
#define lowbit(x) ((x) & -(x))
#define rep(i, s, e) for (int i=(s);i<=(e);++i)
#define all(v) v.begin(), v.end()
#define pb push_back
const LL INF = 1e18 ;
const int mod = 1e9+7;
const int N = 2e5+10;
int dx[4] = {0, 1, 0, -1}, dy[5] = {1, 0, -1, 0};LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;
}LL qmi(int m, int k, int p){int res = 1 % p, t = m;while (k){if (k&1) res = res * t % p;t = t * t % p;k >>= 1;}return res;}int h , n ;
int a[N] , c[N] ;bool pd(LL m){LL dmg = 0 ;rep(i,1,n){dmg += a[i] * ((m+c[i]-1) / c[i]) ;if(dmg>=h) return true ;}return dmg>=h ;
}inline void solve(){cin >> h >> n ;LL sum = 0 ;rep(i,1,n) cin >> a[i] , sum += a[i];rep(i,1,n) cin >> c[i] ;if(sum>=h){cout << 1 << endl ;return ;}LL l = 1 , r = 2e12 ;while(l+1<r){LL m = (l+r)>>1 ;if(pd(m)) r = m ;else l = m ; // cout << l << endl ;}cout << r << endl ;
}signed main(){IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}G
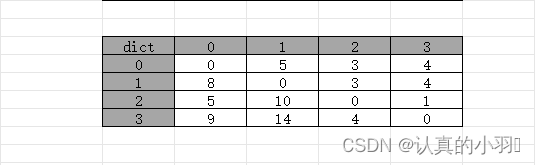
- D(n) : 表示数位和;
- D(k*n) = k*D(n) : 那么n的所有数位上的数x在*k之后不能够进位
- --> 能够推出x<=[9/k] ps : []代表下取整
- 然后计算[10^l,10^r)中有多少个数n满足这个条件
- 对于每一个数位,有t=[9/k]+1 种选择,有r个数位,res=t^r
- ans = t^r-t^l
用快速幂优化一下 :
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
typedef long long LL;
typedef unsigned long long ULL ;
#define PI acos(-1)
#define endl '\n'
#define PII pair<int,int>
#define x first
#define y second
#define no do { cout << "No" << endl; return; } while(0)
#define yes do { cout << "Yes" << endl; return; } while (0)
#define lowbit(x) ((x) & -(x))
#define rep(i, s, e) for (int i=(s);i<=(e);++i)
#define all(v) v.begin(), v.end()
#define pb push_back
const LL INF = 1e18 ;
const int Mod = 1e9+7;
const int N = 2e5+10;
int dx[4] = {0, 1, 0, -1}, dy[5] = {1, 0, -1, 0};LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;
}LL qmi(LL m, LL k, LL p){LL res = 1 % p, t = m;while (k){if (k&1) res = res * t % p;t = t * t % p;k >>= 1;}return res;}inline void solve(){
// D(n) : 表示数位和
// D(k*n) = k*D(n) : 那么n的所有数位上的数x在*k之后不能够进位
// --> 能够推出x<=[9/k] ps : []代表下取整
// 然后计算[10^l,10^r)中有多少个数n满足这个条件
// 对于每一个数位,有t=[9/k]+1 种选择,有r个数位,res=t^r
// ans = t^r-t^lLL l , r , k ; cin >> l >> r >> k ;if(k>=10){cout << 0 << endl ;return ;}int p = floor(1.0*9/k)+1 ;LL ans = (qmi(p,r,Mod) - qmi(p,l,Mod)) % Mod ;if(ans<0) ans += Mod ;cout << ans << endl ;
}signed main(){IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}H
用并查集记录关于每个点的连通块 ;
然后遍历每一行,每一列来求将这一行/列全改为#,之后的连通块的大小,找到最大的;
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
typedef long long LL;
typedef unsigned long long ULL ;
#define PI acos(-1)
#define endl '\n'
#define PII pair<int,int>
#define no do { cout << "No" << endl; return; } while(0)
#define yes do { cout << "Yes" << endl; return; } while (0)
#define lowbit(x) ((x) & -(x))
#define rep(i, s, e) for (int i=(s);i<=(e);++i)
#define all(v) v.begin(), v.end()
#define pb push_back
const LL INF = 1e18 ;
const int mod = 1e9+7;
const int N = 2e5+10;
int dx[4] = {0, 1, 0, -1}, dy[5] = {1, 0, -1, 0};LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : a;
}LL qmi(int m, int k, int p){int res = 1 % p, t = m;while (k){if (k&1) res = res * t % p;t = t * t % p;k >>= 1;}return res;}struct DSU {std::vector<int> f, siz;DSU() {}DSU(int n) {init(n);}void init(int n) {f.resize(n);std::iota(f.begin(), f.end(), 0);siz.assign(n, 1);}int find(int x) {while (x != f[x]) {x = f[x] = f[f[x]];}return x;}bool same(int x, int y) {return find(x) == find(y);}bool merge(int x, int y) {x = find(x);y = find(y);if(x == y) return false;siz[x] += siz[y];f[y] = x;return true;}int size(int x) {return siz[find(x)];}
};inline void solve(){int n ,m ; cin >> n >> m ;vector<string> s(n) ;rep(i,0,n-1) cin >> s[i] ;int sz = n * m ;DSU dsu(sz) ;rep(i,0,n-1){rep(j,0,m-1){if(i+1<n&&s[i][j]=='#'&&s[i+1][j]=='#'){//对行进行扩展 dsu.merge(i*m+j,(i+1)*m+j);//合并 }if(j+1<m&&s[i][j]=='#'&&s[i][j+1]=='#'){dsu.merge(i*m+j,i*m+j+1);//合并 }}}int ans = 0 ;vector<int> vis(sz,-1) ;rep(r,0,n-1){int res = 0 ;rep(i,0,m-1){//修改一行 if(s[r][i]=='.') res ++ ;//修改成#的数目 for(int xx=max(0,r-1);xx<=min(n-1,r+1);xx++){//找上下两行的联通块 if(s[xx][i]=='#'){int u=dsu.find(xx*m+i);if(vis[u]!=r){vis[u] = r ;res += dsu.size(u);}}}}ans = max(ans,res) ;}vis.assign(sz,-1) ;for(int c=0;c<m;c++){int res = 0 ;for(int i=0;i<n;i++){if(s[i][c]=='.') res++ ;for(int y=max(0,c-1);y<=min(m-1,c+1);y++){if(s[i][y]=='#'){int u = dsu.find(i*m+y);if(vis[u]!=c){vis[u] = c ;res += dsu.size(u) ;}}}}ans = max(ans,res) ;}cout << ans << endl ;
}signed main(){IOSint _ = 1;cin >> _;while(_ --) solve();return 0;
}相关文章:
 c++题解(A-H1))
Codeforces Round 952 (Div. 4) c++题解(A-H1)
开头 : 这场没打,今天vp了一下,写了A-G,然后就去吃饭了! 比赛链接 : Dashboard - Codeforces Round 952 (Div. 4) - Codeforces A 直接交换,输出即可 inline void solve(){string a , b ; cin >> a>> b ;char c a[0] ;a…...

人工智能将成为数学家的“副驾驶”
人工智能将成为数学家的“副驾驶” 数学传统上是一门独立的科学。1986年,安德鲁怀尔斯为了证明费马定理,退到书房里呆了7年。由此产生的证明往往很难让同事们理解,有些至今仍有争议。但近年来,越来越多的数学领域被严格地分解为各…...

自适应巡航控制技术规范(简化版)
自适应巡航控制技术规范(简化版) 1 系统概述2 功能需求3 性能需求4 功能激活条件5 功能抑制条件6 系统局限性1 系统概述 ACC 自适应巡航系统可自动控制纵向跟车距离,减轻驾驶员的工作量,即驾驶员无需频繁的踩制动和油门便可完成部分的驾驶任务,但责任主体仍然是驾驶员,驾…...

【AI】文心一言的使用分享
在数字化时代,人工智能(AI)技术的飞速发展正在改变我们的生活。文心一言,作为这一浪潮中的佼佼者,以其卓越的自然语言处理能力和广泛的应用场景,给我带来了前所未有的使用体验。在这篇分享中,我…...
)
Java学习-MyBatis学习(四)
代码下载 解决字段名与属性名不一致 ①使用别名emp_name empName解决字段名和属性名不一致 <select id"getAllEmpOld" resultType"Emp"><!--①使用别名emp_name empName解决字段名和属性名不一致-->select eid,emp_name empName,age,sex,em…...
多源最短路径算法 -- 弗洛伊德(Floyd)算法
1. 简介 Floyd算法,全名为Floyd-Warshall算法,亦称弗洛伊德算法或佛洛依德算法,是一种用于寻找给定加权图中所有顶点对之间的最短路径的算法。这种算法以1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特弗洛伊德的名字命名。 2. 核心思…...

同三维T80005EH4 H.265 4路高清HDMI编码器
同三维T80005EH4 H.265 4路高清HDMI编码器 4路HDMI输入2路3.5音频输入,第1路和第2路HDMI可支持4K30,其它支持高清1080P60 产品简介: 同三维T80005EH4 4路HDMI高清H.265编码器采用最新高效H.265高清数字视频压缩技术,具备稳定…...

焦化行业排放平台简介
在当今社会,环保事业日益受到人们的关注。焦化行业作为重要的工业领域之一,其排放问题一直是环保工作的重点。为了有效控制焦化行业的排放,实施焦化行业排放平台成为了必不可少的措施。朗观视觉小编将详细探讨焦化行业排放平台的实施范围&…...
『原型资源』Axure自带图标库不够用,第三方经典图标库来袭
今天小编为大家带来第三方经典图标库,己确认内容可用现推荐给大家。直接上手就可不用自己画哈~ 获取原型文档请与班主任联系! 先睹为快,合适再拿走不谢: 图标太多,截取部分给大家参考o(* ̄︶ ̄*…...

修改版的VectorDBBench更好用
原版本VectorDBBench的几个问题 在这里就不介绍VectorDBBench是干什么的了,上官网即可。 1.并发数设置的太少 2.测试时长30秒太长 3.连接milvus无用户和密码框,这个是最大的问题 4.修改了一下其它参数 由于很多网友发私信问一些milvus的相关技术问…...

六西格玛培训都培训哪些内容 ?
天行健六西格玛培训的内容通常涵盖多个方面,旨在帮助学员全面理解和应用六西格玛管理方法。以下是详细的培训内容概述: 一、六西格玛基础知识 引入六西格玛的概念、原理和历史,包括DMAIC(定义、测量、分析、改进、控制࿰…...

K8S环境部署Prometheus
K8S环境部署Prometheus 记录在K8S 1.18版本环境下部署Prometheus 0.5版本。 1. 下载kube-prometheus仓库 git clone https://github.com/coreos/kube-prometheus.git cd kube-prometheus笔者安装的K8S版本是1.18 ,prometheus选择配套的分支release-0.5࿱…...

在linux系统上挂载新硬盘
服务器的硬盘空间不够了,自己重新安装了一个硬盘,需要挂载,因为只是用来存放数据,所以不需要分区,直接挂载就可以 #查看当前所有硬盘 sudo fdisk -l #用于显示文件系统的磁盘空间使用情况 df -h发现一个/dev/nvme0n1 …...

1004.最大连续1的个数
给定一个二进制数组 nums 和一个整数 k,如果可以翻转最多 k 个 0 ,则返回 数组中连续 1 的最大个数 。 示例 1: 输入:nums [1,1,1,0,0,0,1,1,1,1,0], K 2 输出:6 解释:[1,1,1,0,0,1,1,1,1,1,1] 粗体数字…...

【机器学习300问】116、什么是序列模型?序列模型能干什么?
一、序列模型是什么? 序列模型是机器学习领域中专门设计来处理具有时间顺序或序列结构数据的模型。这类模型能够理解和学习数据中的顺序依赖关系,因此非常适合诸如自然语言处理、语音识别、音乐生成、时间序列预测等任务。 看了上面的定义,似…...

kafka 快速上手
下载 Apache Kafka 演示window 安装 编写启动脚本,脚本的路径根据自己实际的来 启动说明 先启动zookeeper后启动kafka,关闭是先关kafka,然后关闭zookeeper 巧记: 铲屎官(zookeeper)总是第一个到,最后一个走 启动zookeeper call bi…...

Python记忆组合透明度语言模型
🎯要点 🎯浏览器语言推理识别神经网络 | 🎯不同语言秽语训练识别数据集 | 🎯交互式语言处理解释 Transformer 语言模型 | 🎯可视化Transformer 语言模型 | 🎯语言模型生成优质歌词 | 🎯模型不确…...
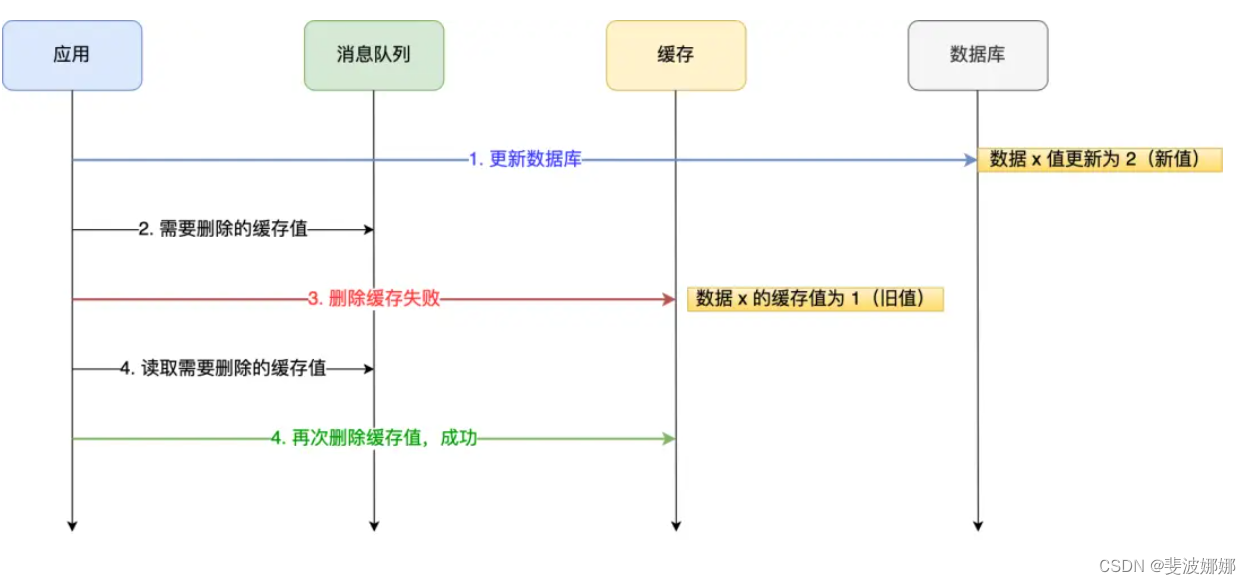
如何保证数据库和缓存的一致性
背景:为了提高查询效率,一般会用redis作为缓存。客户端查询数据时,如果能直接命中缓存,就不用再去查数据库,从而减轻数据库的压力,而且redis是基于内存的数据库,读取速度比数据库要快很多。 更新…...

Java基础 - 多线程
多线程 创建新线程 实例化一个Thread实例,然后调用它的start()方法 Thread t new Thread(); t.start(); // 启动新线程从Thread派生一个自定义类,然后覆写run()方法: public class Main {public static void main(String[] args) {Threa…...

云顶之弈-测试报告
一. 项目背景 个人博客系统采用前后端分离的方法来实现,同时使用了数据库来存储相关的数据,同时将其部署到云服务器上。前端主要有四个页面构成:登录页、列表页、详情页以及编辑页,以上模拟实现了最简单的个人博客系统。其结合后…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
