【three.js】自定义物体形状BufferGeometry
目录
一、认识缓冲类型几何体BufferGeometry
二、将各个顶点连线
一、认识缓冲类型几何体BufferGeometry
threejs的长方体BoxGeometry、球体SphereGeometry等几何体都是基于BoxGeometry类构建的,BufferGeometry是一个没有任何形状的空几何体,你可以通过BufferGeometry自定义任何几何形状,具体一点说就是定义顶点数据。
//创建一个空的几何体对象
const geometry = new THREE.BufferGeometry();
//类型化数组创建顶点数据
const vertices = new Float32Array([0, 0, 0, //顶点1坐标50, 0, 0, //顶点2坐标0, 100, 0, //顶点3坐标0, 0, 10, //顶点4坐标0, 0, 100, //顶点5坐标50, 0, 10, //顶点6坐标
]);
// 创建属性缓冲区对象
//3个为一组,表示一个顶点的xyz坐标
const attribue = new THREE.BufferAttribute(vertices, 3);
// 设置几何体attributes属性的位置属性
geometry.attributes.position = attribue;// 点渲染模式
const material = new THREE.PointsMaterial({color: 0xffff00,size: 10.0 //点对象像素尺寸
});
const point相关文章:

【three.js】自定义物体形状BufferGeometry
目录 一、认识缓冲类型几何体BufferGeometry 二、将各个顶点连线 一、认识缓冲类型几何体BufferGeometry threejs的长方体BoxGeometry、球体SphereGeometry等几何体都是基于BoxGeometry类构建的,BufferGeometry是一个没有任何形状的空几何体,你可以通过BufferGeometry自定…...

Mac 使用 Homebrew 安装 Python3
在macOS系统中,使用Homebrew安装Python3并进行环境配置的步骤如下: 打开终端。 运行以下命令安装Python3: brew install python3 安装完成后,可以通过以下命令检查Python3的版本: python3 --version 为了确保终端…...
汽车行驶中是怎么保障轴瓦安全的?
汽车轴瓦是一种用于减少摩擦和支撑转动部件的关键零部件,通常用于发动机的曲轴、凸轮轴等转动部件上。主要作用是减少转动部件之间的摩擦,支撑和保护曲轴、凸轮轴等旋转部件,确保它们在高速旋转时的稳定性和耐用性。 在汽车轴瓦加工过程中&am…...

洗地机哪款好?洗地机十大名牌排行榜
随着科技的发展,各种家居清洁工具层出不穷,为我们的生活带来了诸多便利。在众多清洁工具中,洗地机的清洁效果更受大家喜爱,它能够完美解决了扫地机无法做到的干湿垃圾“一遍清洁”效果,而且几乎能解决日常生活中所有的…...
)
spark mllib 特征学习笔记 (二)
当然,请继续介绍其他特征处理方法的公式、适用场景和案例: 10. StringIndexer 公式: 将字符串类型的标签转换为数值索引: StringIndexer ( x ) { 0 , 1 , 2 , … , N − 1 } \text{StringIndexer}(x) \{0, 1, 2, \ldots, N-1…...

湘潭大学软件工程数据库2(题型,复习资源和计划)
文章目录 选择题关系范式事务分析E-R 图sql作业题答案链接(仅限有官方答案的版本)结语 现在实验全部做完了,实验和作业占比是百分之 40 ,通过上图可以看出来,重点是 sql 语言 所以接下来主要就是学习 sql 语句怎么书写…...

第二十三节:带你梳理Vue2:Vue插槽的认识和基本使用
前言: 通过上一节的学习,我们知道了如何将数据从父组件中传递到子组件中, 除了除了将数据作为props传入到组件中,Vue还允许传入HTML, Vue 实现了一套内容分发的 API,这套 API 的设计灵感源自 Web Components 规范草案,将 <slot> 元素作为承载分发…...
父亲节马上到了-和我一起用Python写父亲节的祝福吧
前言 让我们一起用Python写一段父亲节的祝福吧 📝个人主页→数据挖掘博主ZTLJQ的主页 个人推荐python学习系列: ☄️爬虫JS逆向系列专栏 - 爬虫逆向教学 ☄️python系列专栏 - 从零开始学python 话不多说先上代码 import tkinter as tk from doctest imp…...
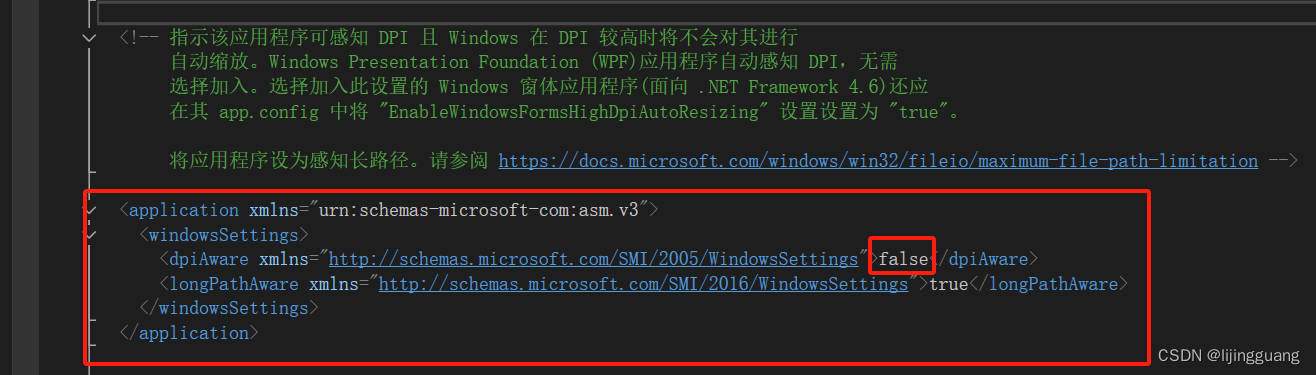
winform 应用程序 添加 wpf控件后影响窗体DPI改变
第一步:添加 应用程序清单文件 app.manifest 第二步:把这段配置 注释放开,第一个配置true 改成false...

Web前端开发素材:探索、选择与应用的艺术
Web前端开发素材:探索、选择与应用的艺术 在Web前端开发的广袤领域中,素材的选择与应用无疑是一项至关重要的技能。它们如同构建网页的砖石,既承载着设计的美感,又影响着用户体验的深度。本文将从四个方面、五个方面、六个方面和…...
LeetCode | 20.有效的括号
这道题就是栈这种数据结构的应用,当我们遇到左括号的时候,比如{,(,[,就压栈,当遇到右括号的时候,比如},),],就把栈顶元素弹出,如果不匹配,则返回False,当遍历完所有元素后…...

ceph scrub 错误记录
目的 记录 ceph scrub 错误问题解决 ceph scrub 故障故障信息 cluster:id: xxx-xxx-xxxhealth: HEALTH_ERR2 scrub errorsPossible data damage: 2 pg inconsistentmessage 日志信息 # egrep -i medium|i\/o error|sector|Prefailure /var/log/messages Jun 15 00:23:37 m…...

cs与msf权限传递,以及mimikatz抓取明文密码
cs与msf权限传递,以及mimikatz抓取win10明文密码 1、环境准备2、Cobalt Strike ------> MSF2.1 Cobalt Strike拿权限2.2 将CS权限传递给msf 3、MSF ------> Cobalt Strike3.1 msf拿权限3.2 将msf权限传递给CS 4、使用mimikatz抓取明文密码 1、环境准备 攻击&…...

Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式
Windows下的zip压缩包版Mysql8.3.0数据迁移到Mysql8.4.0可以用拷贝data文件夹的方式 拷贝后, 所有账户和数据都是一样的 步骤 停止MySQL服务 net stop mysql 或 sc.exe stop mysql net stop mysqlsc.exe stop mysql卸载 Mysql8.3.0 的服务 mysqld remove 或 mysqld remove m…...
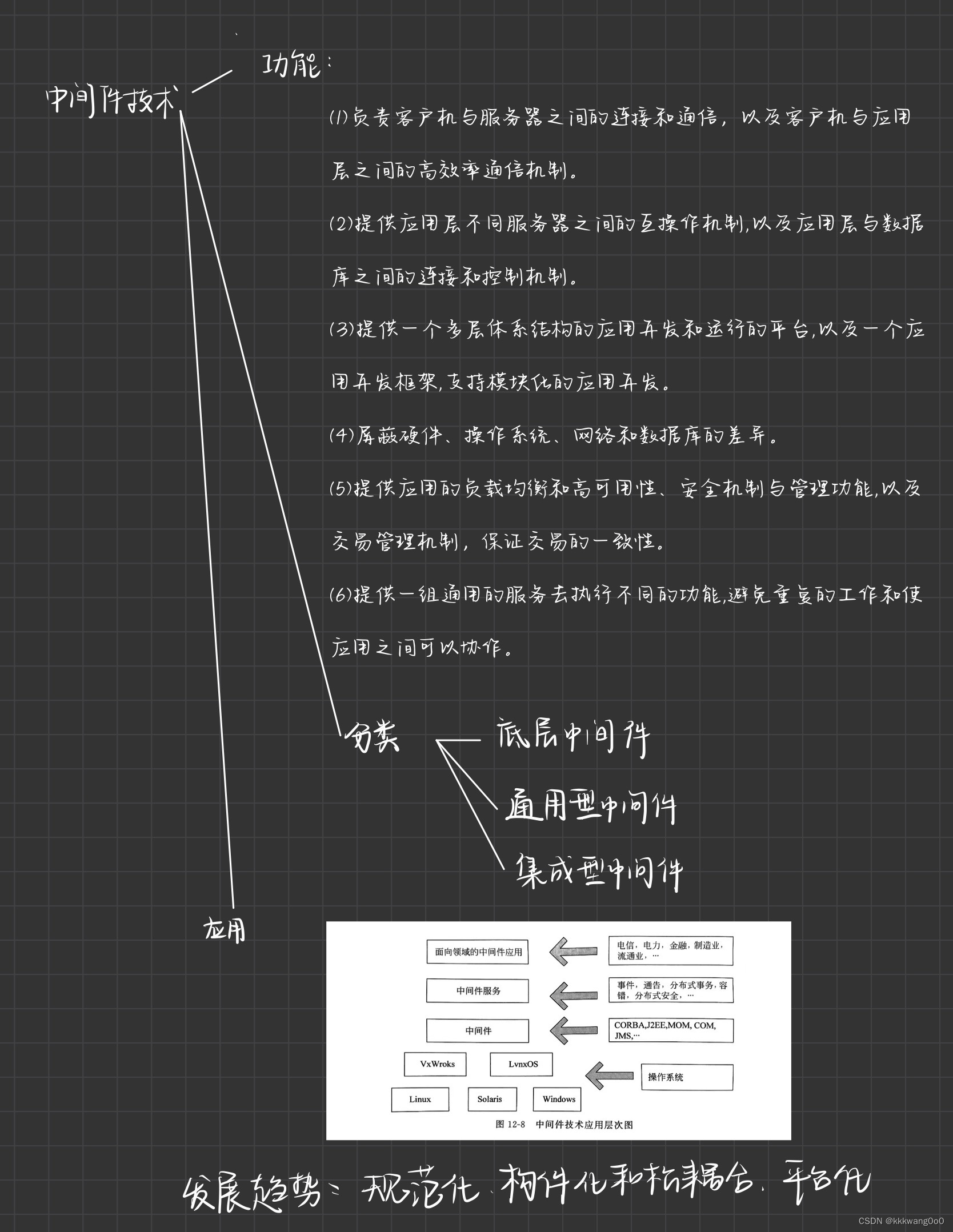
软件体系结构笔记(自用)
来自《软件体系结构原理、方法与实践(第三版)》清华大学出版社 张友生编著 1-8章12章 复习笔记 如有错误,欢迎指正!!!...

java安装并配置环境
安装前请确保本机没有java的残留,否则将会安装报错 1.安装java jdk:安装路径Java Downloads | Oracle 中国 百度网盘链接:https://pan.baidu.com/s/11-3f2QEquIG3JYw4syklmQ 提取码:518e 2.双击 按照流程直接点击下一步&#x…...
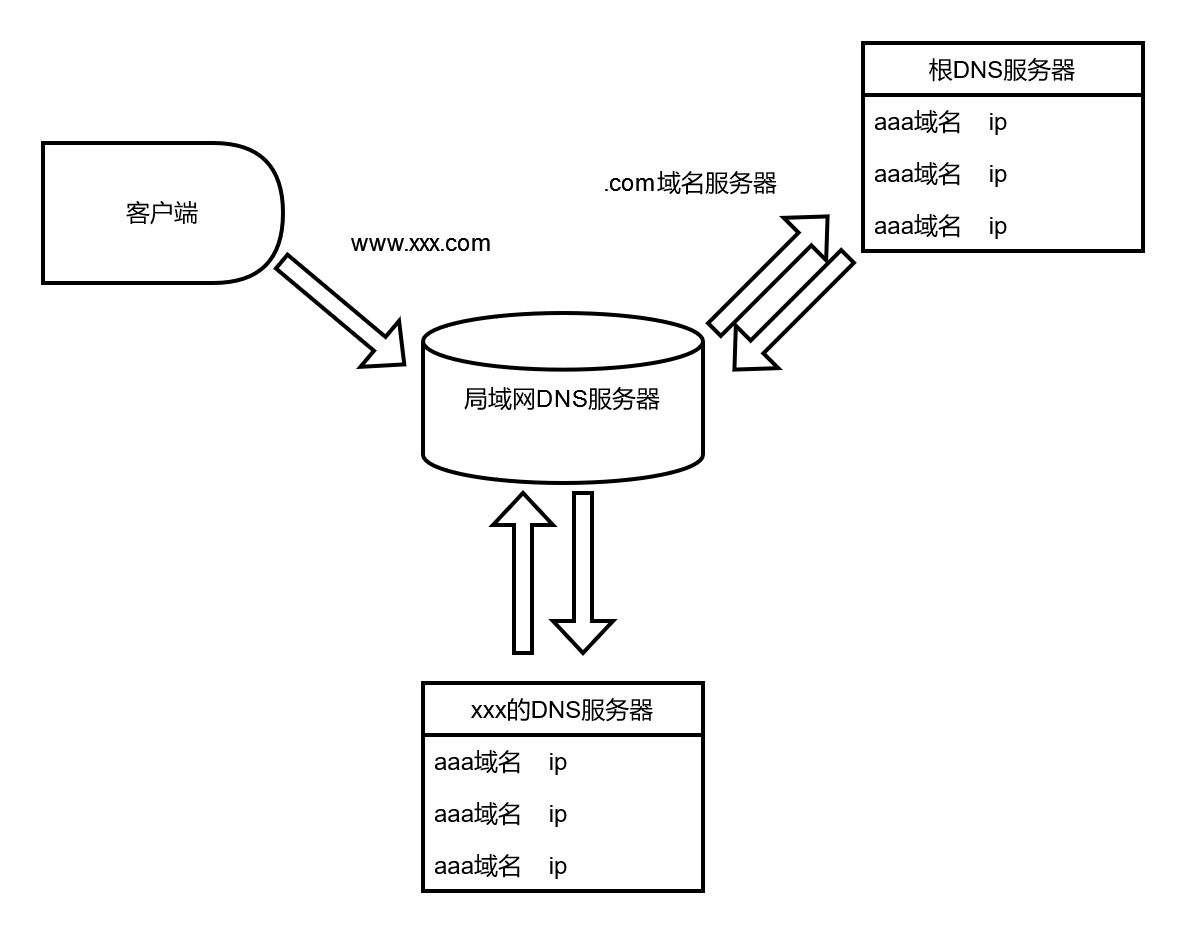
探索互联网寻址机制 | 揭秘互联网技术的核心,解析网络寻址
揭秘互联网技术的核心,解析网络寻址题 前提介绍局域网地址IP地址的分配方式动态IP分配机制内部网(intranet)ICANN负责IP分配DHCP协议获取IP地址 域名系统域名是什么域名工作方式hosts文件存储域名映射关系DNS分布式数据库DNS域名解析 Java进行…...
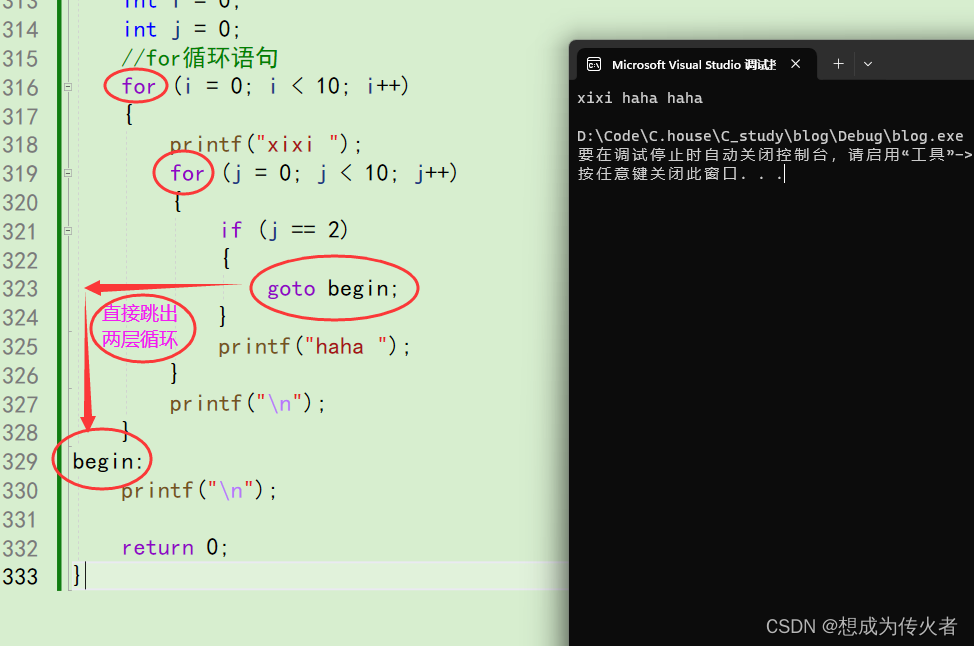
C语言学习笔记之结构篇
C语言是一门结构化程序设计语言。在C语言看来,现实生活中的任何事情都可看作是三大结构或者三大结构的组合的抽象,即顺序,分支(选择),循环。 所谓顺序就是一条路走到黑;生活中在很多事情上我们都…...

C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法
C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法 —— 2024-06-08 杭州 code review! 文章目录 C++笔记之一个函数多个返回值的方法、std::pair、std::tuple、std::tie的用法一.从一个函数中获取多个返回值的方法1. 使用结构体或类2. 使用`std::t…...

GDB:从零开始入门GDB
目录 1.前言 2.开启项目报错 3.GDB的进入和退出 4.GDB调试中查看代码和切换文件 5.GDB调试中程序的启动和main函数传参 6.GDB中断点相关的操作 7.GDB中的调试输出指令 8.GDB中自动输出值指令 9.GDB中的调试指令 前言 在日常开发中,调试是我们必不可少的技能。在专业…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
