牛客小白月赛68【A-E】
文章目录
- A.Tokitsukaze and New Operation【模拟】
- B.Tokitsukaze and Order Food Delivery【模拟、特判】
- C.Tokitsukaze and Average of Substring【暴力、前缀】
- D.Tokitsukaze and Development Task【记忆化搜索】
- E.Tokitsukaze and Colorful Chessboard【预处理,二分】
链接
传送门
A.Tokitsukaze and New Operation【模拟】
分析
根据题意模拟就行,合理运用STL可以简化代码。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
void solve() {string a, b;cin >> a >> b;int n = a.size(), m = b.size();if (n != m) {cout << -1 << '\n';return;}string ans;for (int i = 0; i < n; i++) {ans += to_string((a[i] - '0') * (b[i] - '0'));//to_stirng函数可以使得int转换为string类型}cout << ans << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) {solve();}
}
B.Tokitsukaze and Order Food Delivery【模拟、特判】
分析
这题看似唬人,其实不难,因为这里只说了取一道菜所以只需暴力取最优的即可。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
void solve() {int n, a, b;cin >> n >> a >> b;int ans = inf;while (n--) {int k, x, y;cin >> k >> x >> y;while (k--) {int c;cin >> c;if (c >= a && c >= x) {c = max(0, c - b - y);} else if (c >= a) {c = max(0, c - b);} else if (c >= x) {c = max(0, c - y);}ans = min(ans, c);}}cout << ans << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;while (T--) {solve();}
}
C.Tokitsukaze and Average of Substring【暴力、前缀】
分析
这里n的范围是5000,我们可以直接枚举两端,对26个字母统计前缀字符数,即可,时间复杂度O(n^2*26),注意可能卡map,这里用数组。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 5005;
char s[N];
int cnt[26][N];
void solve() {int n;scanf("%d", &n);for (int i = 1; i <= n; i++) {for (int j = 0; j < 26; j++) {cnt[j][i] = 0;}}scanf("%s", s + 1);for (int i = 1; i <= n; i++) {char ch = s[i];for (int j = 0; j < 26; j++) {if (ch - 'a' == j) cnt[j][i] = cnt[j][i - 1] + 1;else cnt[j][i] = cnt[j][i - 1];//继承前缀}}
// for (int i = 0; i < 26; i++) {
// for (int j = 1; j <= n; j++) {
// cout << cnt[i][j] << ' ';
// }
// cout << '\n';
// }double ans = 0;for (int i = 1; i <= n; i++) {for (int j = i; j <= n; j++) {int sum = 0;for (int k = 0; k < 26; k++) {int c = cnt[k][j] - cnt[k][i - 1];sum += c * (c - 1) / 2;//统计相同的对数}ans = max(ans, 1.0 * sum / (j - i + 1));}}printf("%.6lf\n", ans);
}
int main() {
// ios::sync_with_stdio(false);
// cin.tie(0);int T = 1;cin >> T;while (T--) {solve();}
}
D.Tokitsukaze and Development Task【记忆化搜索】
分析
首先300的数目步数最多300,总共有8种更新方法,求最小操作次数,但是这里组数有点多,考虑用记忆化搜索,总时间复杂度为O(n^2).
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 5005;
int go[6] = {1, -1, 10, -10, 100, -100};
int dp[305];
bool vis[305];
void bfs(int tar) {for (int i = 10; i <= 300; i++) vis[i] = 0;vis[10] = 1;queue<PII> q;q.push({10, 0});while (!q.empty()) {int x = q.front().first, s = q.front().second;if (x == tar) {//找到目标值就弹出,先进先出,所以步数是最小的dp[tar] = s;return;}q.pop();for (int i = 0; i < 8; i++) {int nx;if (i < 6) nx = x + go[i];else if (i == 6) nx = 10;else nx = 300;if (nx < 10 || nx > 300 || vis[nx]) continue;vis[nx] = 1;int ns = s + 1;q.push({nx, ns});}}
}
void solve() {int a, b, c, d;
// cin >> a;
// bfs(a);
// cout << dp[a] << '\n';cin >> a >> b >> c >> d;if (dp[a] == -1) bfs(a);if (dp[b] == -1) bfs(b);if (dp[c] == -1) bfs(c);if (dp[d] == -1) bfs(d);cout << dp[a] + dp[b] + dp[c] + dp[d] << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;for (int i = 11; i <= 305; i++) dp[i] = -1;//0也算,所以初始化-1while (T--) {solve();}
}
E.Tokitsukaze and Colorful Chessboard【预处理,二分】
分析
为了更加充分地利用空间,我们需要紧凑地使用格子,所以把棋盘分成奇数格和偶数格使用,预处理平方数,可以得到所有奇数格的数目和偶数格的数目,如果平方数是偶数则两者一样多否则奇数多1个,我们查询的两个数较大的那一个放在奇数格上,利用二分,但是,此时另一个数可能不行,因为如果说这个数是对应的平方数是奇数,而两者又是一样大的话,是无法放入的,例如:n=3,b[3]=5,c[3] = 4, x = y = 5,必须往右挪一格(可能前面有需要几格的,但是不多)到y符合,在向右挪的时候由于单调性,x始终符合。注意爆int。
实现
#include <bits/stdc++.h>
#define ll long long
#define ls (u << 1)
#define rs (u << 1 | 1)
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 5;
int go[6] = {1, -1, 10, -10, 100, -100};
ll a[N], b[N], c[N];
void solve() {ll x, y;cin >> x >> y;if (x < y) swap(x, y);int n = 1e5;int p = lower_bound(b + 1, b + 1 + n, x) - b;
// cout << b[p] << '\n';while (c[p] < y) p++;//稍微挪一格左右cout << p << '\n';
}
int main() {ios::sync_with_stdio(false);cin.tie(0);int T = 1;cin >> T;int m = 1e5;for (int i = 1; i <= m; i++) a[i] = 1ll * i * i;//这里爆intfor (int i = 1; i <= m; i++) {b[i] = (a[i] + 1) / 2;c[i] = a[i] - b[i];}
// cout << b[70000] << '\n';
// for (int i = 1; i <= 5; i++) cout << c[i] << '\n';while (T--) {solve();}
}
相关文章:

牛客小白月赛68【A-E】
文章目录A.Tokitsukaze and New Operation【模拟】B.Tokitsukaze and Order Food Delivery【模拟、特判】C.Tokitsukaze and Average of Substring【暴力、前缀】D.Tokitsukaze and Development Task【记忆化搜索】E.Tokitsukaze and Colorful Chessboard【预处理,二…...

WIFI P2P架构
WI-FI P2P定义架构3个组件组织结构技术标准P2P DiscoveryDevice Discovery(扫描)流程p2p probe 管理帧Group Formation(组网)GO Negotiation(GON)流程P2P Public Action管理帧Provision Discoveryÿ…...

架构师之中台思维_系统发展之路_结果和抽象之间平衡的艺术
父文章 如何成为一名架构师,架构师成长之路_golang架构师成长之路_个人渣记录仅为自己搜索用的博客-CSDN博客 任何系统的发展都是如此. 1. 业务增长 2. 烟囱增长 _ 结果优先 _ 太快去抽象抽象不好 3. 太多的烟囱, 3.1 抽象复用为平台 3.2 面对更多新的业务,提供不同的枚举值…...

23届非科班选手秋招转码指南
1.秋招情况介绍 1.1自我介绍 我是一名23届非科班转码选手,本硕均就读于某211院校机械专业,秋招共计拿下12份offer,包括大疆创新、海康威视、联发科技、理想汽车、中电28、阳光电源等各行业、各种性质企业的意向。主要的投递岗位为嵌入式软件…...

《传感器技术》考试学习笔记
文章目录一、选择题二、简答题1.什么是传感器?传感器的共性是哪些?2.差动变气隙式传感器电感传感器的灵敏度推导过程是什么(推导公式)?与单极性进行比较它们的优缺点是哪些?3.霍尔传感器如何进行微位移测量…...
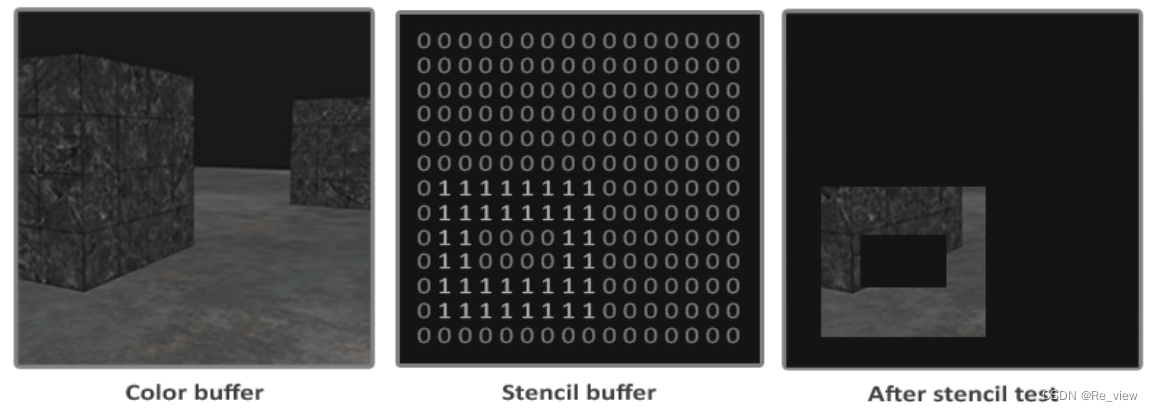
第十五章 opengl之高级OpenGL(模板测试)
OpenGL模板测试模板函数物体轮廓模板测试 当片段着色器处理完一个片段后,模板测试就会开始执行。类似于深度测试,模板测试也可能会丢弃片段。被保留的片段会进入深度测试,可能会丢弃更多的片段。 模板测试是根据模板缓冲来进行的。一个模板缓…...
【C语言蓝桥杯每日一题】—— 单词分析
【C语言蓝桥杯每日一题】—— 单词分析😎前言🙌单词分析🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者…...

Web2:Tomcat
二.Web2:Tomcat 1.Tomcat的配置 2.Tomcat的工作方式 3.Tomcat服务器的虚拟映射 4.Tomcat部署到IDEA中使用 二.Web2:Tomcat 1.Tomcat的配置 ①安装下载Tomcat 配置好JAVA_HOME启动时保证端口号8080不被占用 ②下载后的目录结构 bin 启动或关闭to…...

C++语法规则2(C++面向对象)
继承 面向对象程序设计中最重要的一个概念是继承。继承允许我们依据另一个类来定义一个类,这使得创建和维护一个应用程序变得更容易。这样做,也达到了重用代码功能和提高执行效率的效果。 当创建一个类时,您不需要重新编写新的数据成员和成…...
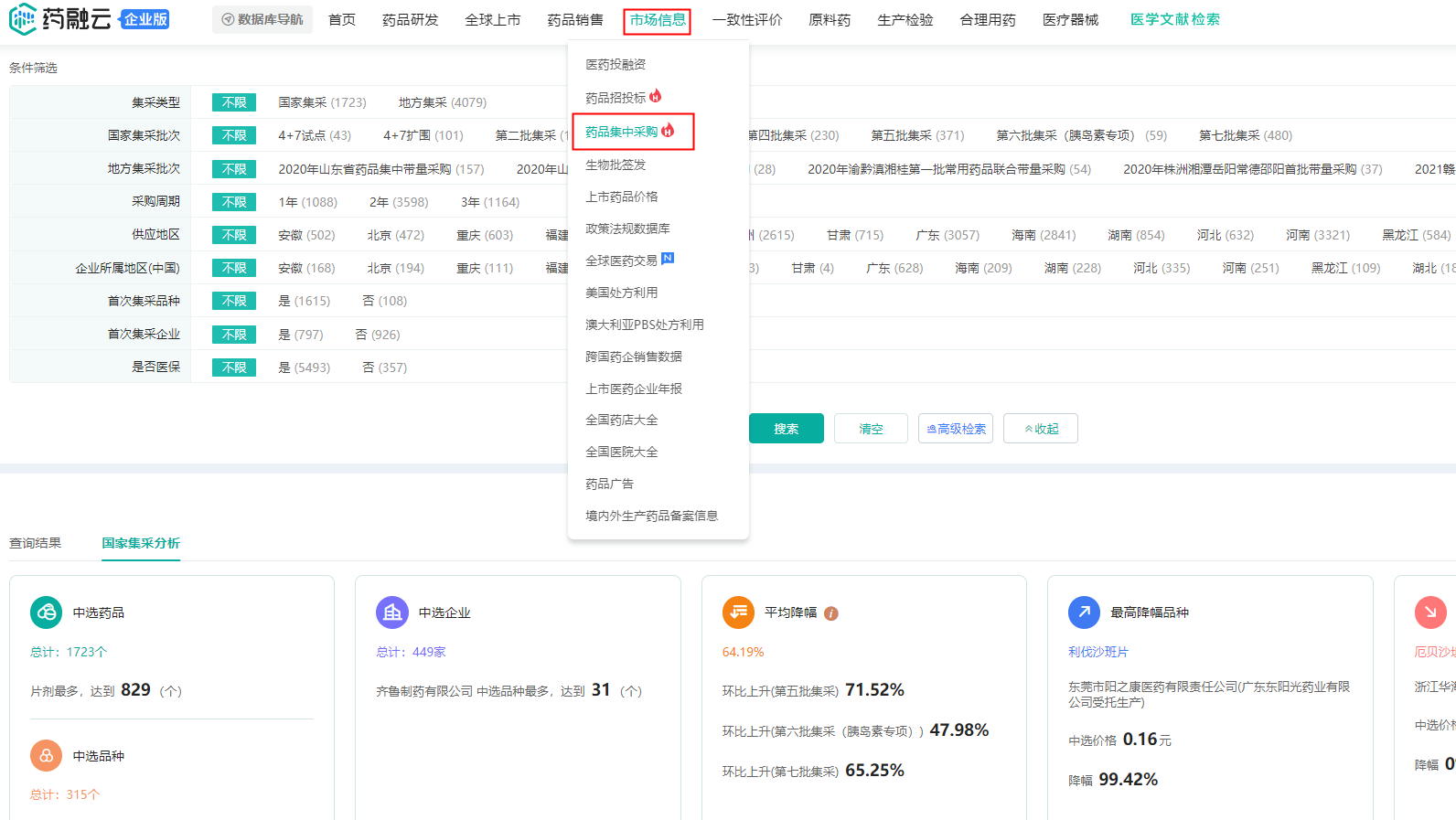
第八批国家药品集中采购-(附药品集采目录明细下载)
2023年3月2日,‘国家组织药品联合采购办公室’发出了《全国药品集中采购文件》,宣告了第八批国家组织药品集中采购工作正式开展,其公告中还包含三个附表分别为‘采购品种目录’、‘各地区首年约定采购量’、‘各采购品种首年约定采购量’&…...
政府工作报告连提9年科技创新 企业研发如何“又快又好”
今年的政府工作报告, “科技创新” 这一描述连续出现7次,这也是自2015年开始, “科技创新” 这一概念在全国“两会”政府工作报告中连续九年被提到。政府工作报告指出,科技政策要聚焦自立自强,完善新型举国体制&#x…...
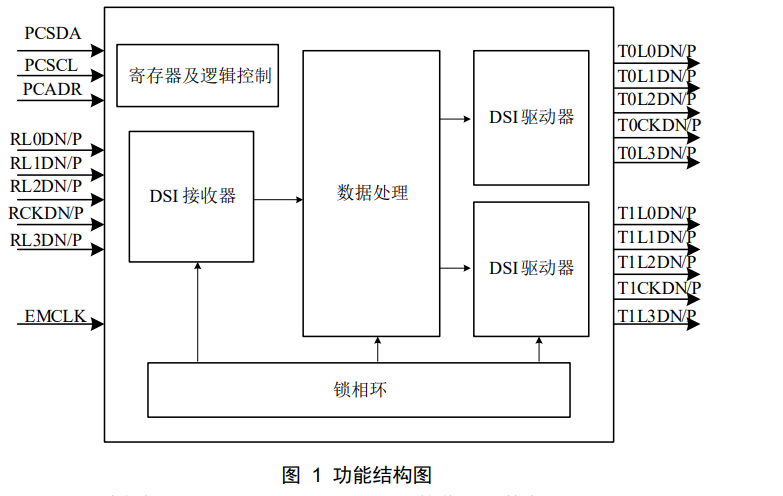
GM8773C 是一款 1:2 DSI 桥接芯片,可实现 4 路进 8 路出转换器功能、视频分离器功能。
GM8773C 是一款 1:2 DSI 桥接芯片,可实现 4 路进 8 路出转换器功能、视频分离器功能。芯片内集成了一个 4 路单一链路的 MIPI DSI 接收器和 8 路双链路 MIPI DSI 发送器。 接 收 器 每 路 可 以 支 持 到 2.0Gbps/lane , 可 以 最 高 支 持 到…...

Java常用包名和说明
包名主要功能java.applet提供了创建applet需要的所有类java.awt.*提供了创建用户界面以及绘制和管理图形、图像的类java.beans.*提供了开发Java Beans需要的所有类java.io提供了通过数据流、对象序列以及文件系统实现的系统输入、输出java.lang.*Java编程语言的基本类库java.ma…...
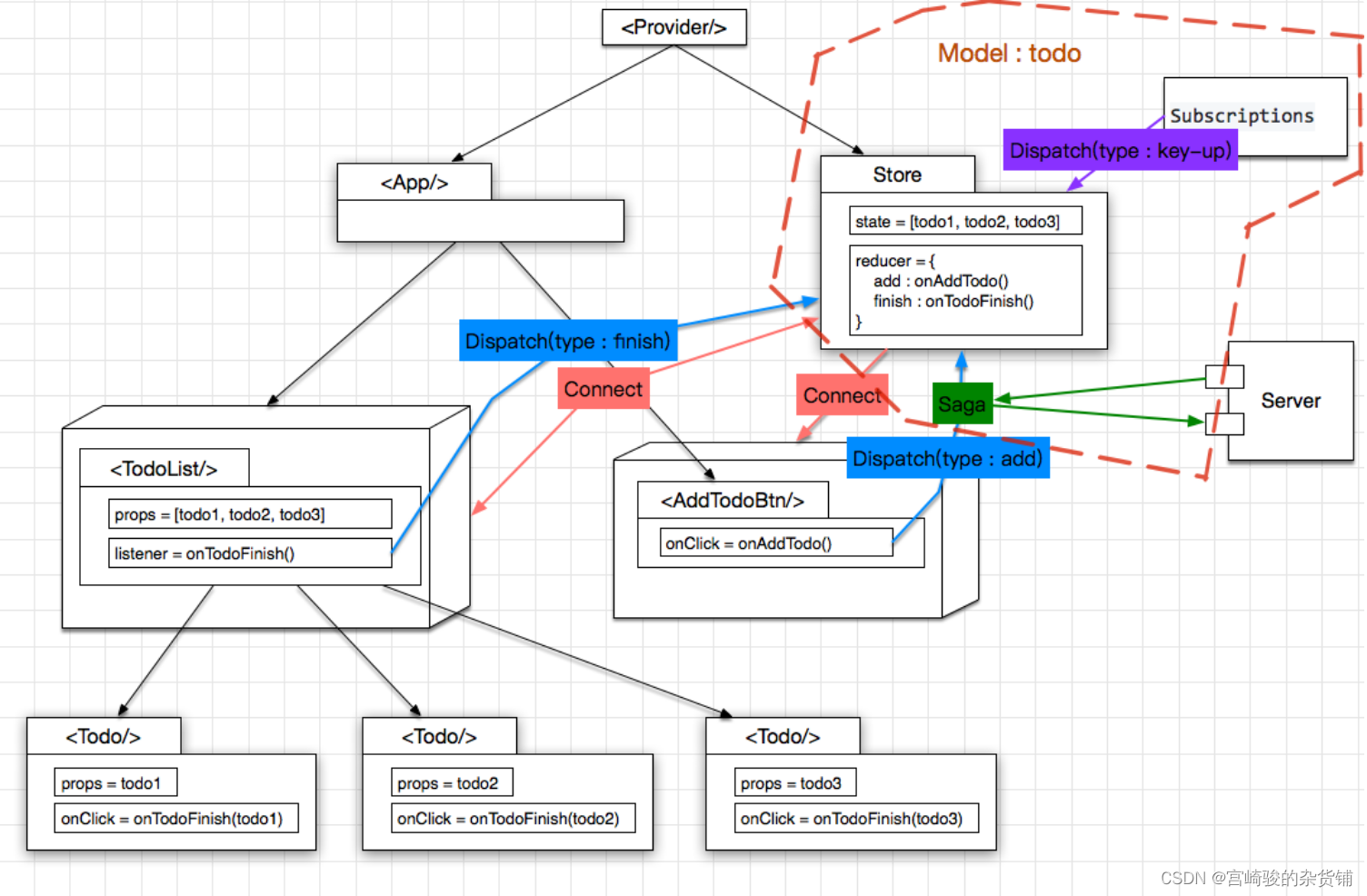
dva01-初识
背景 React 本身只是一个 DOM 的抽象层,使用组件构建虚拟 DOM。如果开发大应用,还需要解决一个问题。 通信:React 只提供了一种传参手段,后续数据变化非常麻烦,无法适用于大应用。数据流:每次要更新数据&…...

信捷 XDH Ethercat A_WRITE指令
本指令修改指令轴的当前位置。 什么时候需要用本指令呢?换句话说,用本指令后,坐标原点修改了偏移了。如果在回原点后,往前走了一段距离x,如果是用绝对模式执行把位置修改成0,那么下一次开始每次做绝对运动A_MOVEA&…...
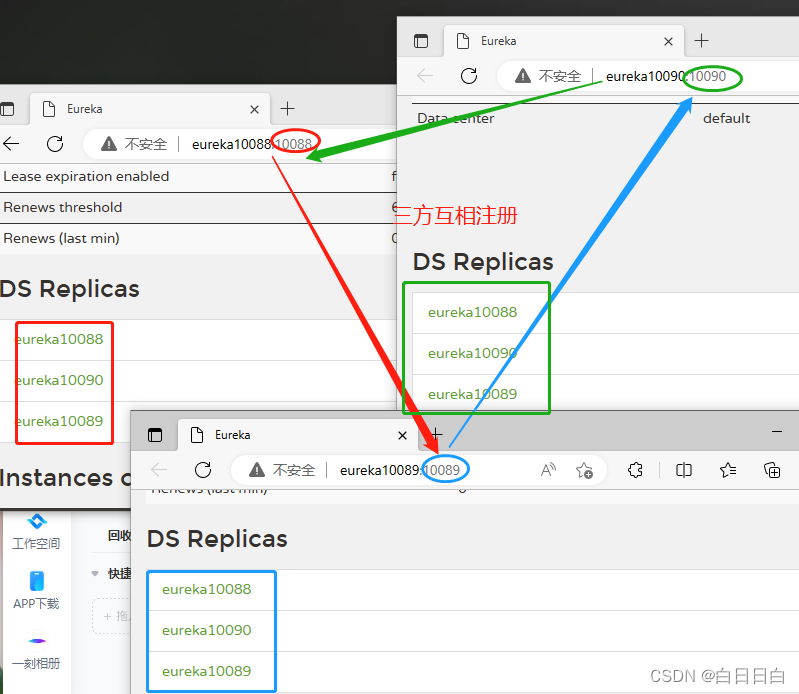
Spring Cloud ( Eureka集群的搭建 )
操作步骤: 添加主机映射创建Eureka服务 导入依赖编写启动类编写yml复制服务实例测试一、添加主机映射 以 Windows系统为例,如果要构建集群,需要修改 hosts 文件,为其添加主机名的映射。 打开C:\Windows\System32\drivers\etc\h…...

Python re 模块
正则表达式是一种小型、高度专业化的编程语言。适用于任何语言,在 Python 中通过 re 模块实现。正则模式被编译成一系列的字节码,然后由 C 语言编写的匹配引擎执行。给字符串模糊匹配 正则用于匹配字符串,匹配字符串可以完全匹配和模糊匹配&…...

为什么越来越多的人开始学习大数据
因为根据国内的发展形势,大数据未来的发展前景会非常好,前景好需求高,自然会吸引越来越多的人进入大数据行业 我国市场环境处于急需大数据人才但人才不足的阶段,所以未来大数据领域会有很多的就业机遇。 2022年春季,…...
---引用)
【C++】C++核心编程(二)---引用
1.基本语法 作用:给变量起别名 语法:数据类型 &别名 原名(int &b a,其中别名与原名的数据类型必须一致) 注意事项: 引用必须初始化引用在初始化后,就不可以再改变了 代码演示&am…...

原型设计模式
介绍 原型模式 在Java中,原型模式是一种创建型设计模式,它允许通过复制一个现有对象来创建一个新对象,而不是通过创建新的对象来初始化一个对象,原型模式是一种基于克隆的设计模式,通过复制现有对象的数据来创建新的对象. 原型模式需要实现Cloneable接口并重写Object类中的c…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
