【数据结构】排序(下)

个人主页~
排序(上)
栈和队列
排序
- 二、常见排序的实现
- 8、快速排序的优化
- 9、非递归快速排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 10、归并排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 11、非递归归并排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 12、非比较排序
- (1)基本思想
- (2)代码实现
- (3)时间复杂度
- (4)空间复杂度
- 三、各个排序方法所用时间的比较
- 1、代码实现
- 2、分析
- 四、各个排序的稳定性
- 1、基本概念
- 2、各个排序的稳定性复杂度一览表
二、常见排序的实现
8、快速排序的优化
当我们使用快速排序时,最坏的情况就是数组有序,此时的时间复杂度为O(N^2)
最好的情况就是key每次取中位数
所以我们为了避免最坏情况的发生,我们在快速排序的基础上衍生了一种优化的方法叫做三数取中
还有一种方法是随机选key,但随机选key的效果不如三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[left] < a[right])return right;elsereturn left;}else{if (a[mid] > a[right])return mid;else if (a[left] > a[right])return right;elsereturn left;}
}
将三个比较出中间的数字作为key然后换到left上,进行partsort
在每个partsort的最前边加上这条语句,就优化了这个快速排序的结构
int PartSort(int* a, int left, int right)
{int midi = GetMidIndex(a, left, right);Swap(&a[left], &a[midi]);......
}
9、非递归快速排序
(1)基本思想
前边我们讲的快速排序是基于递归条件下实现的,但我们知道,递归会消耗栈上的空间,并且栈上的空间比较小,不能实现大量数据的快速排序,所以我们要将这个过程放在空间更大的堆上,也就是使用栈来实现
栈的作用就是存储区间,这个区间由两个整数组成,通过出入栈来模拟递归的过程
(2)代码实现
这里需要包含一下以前我们写过的栈的头文件
void QuickSortNonR(int* a, int left, int right)
{Stack st;StackInit(&st);StackPush(&st,right);StackPush(&st, left);while (!StackEmpty(&st)){int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);//取出区间int keyi = PartSort1(a, left, right);//通过keyi将数据区间一分为二if (keyi + 1 < right){StackPush(&st, right);StackPush(&st, keyi + 1);}if (left < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, left);}//存入区间}StackDestroy(&st);
}
(3)时间复杂度
同递归方式的快速排序,为O(log₂N * N)
(4)空间复杂度
同递归方式的快速排序,为O(log₂N)
10、归并排序
(1)基本思想
将一个待排序的序列分为若干个子序列,每个子序列都是有序的,然后再将有序的序列合并为整体的有序序列
(2)代码实现
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left == right)return;//找到中间下标int midi = (left + right) / 2;//一分为二二分为四的分开_MergeSort(a, left, midi, tmp);_MergeSort(a, midi + 1, right, tmp);int begin1 = left, end1 = midi;int begin2 = midi + 1, end2 = right;//i用来记录容器数组中对应的下标int i = left;//将两个数组中按升序归并到容器数组中while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}//如果左右两个区间的数字还没有全部入到容器数组中,将它们按顺序输入while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];//将容器数组复制到原来的数组上memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
(3)时间复杂度
归并排序分为两个过程
一是分解过程,这是一个类二叉树的过程,由中间下标分为两个区间,再分为四个区间,以此类推,此过程的时间复杂度是O(log₂N)
二是合并过程,合并过程中需要遍历整个数组,找到谁大谁小然后排序,这个过程的时间复杂度是O(N)
整个过程的时间复杂度就是O(N*log₂N)
(4)空间复杂度
该过程需要在堆上开辟n个空间,以及递归所需要的log₂n个在栈上的空间,由于对于n来说log₂n很小,所以它的空间复杂度为O(N)
11、非递归归并排序
(1)基本思想
与快速排序相同,递归方式的归并排序需要使用栈中空间,在处理大量数据时空间不够,所以我们可以用循环的方法减少栈的使用,这就是非递归的归并排序
(2)代码实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);int gap = 1;while (gap < n){int j = 0;//作为tmp的下标for (int i = 0; i < n; i += 2*gap)//每次跳过两组数据{//这里的间隔差gap,每次比较两组数据int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;//以下同上if (end1 >= n || begin2 >= n)break;if (end2 >= n)end2 = n - 1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2])tmp[j++] = a[begin1++];elsetmp[j++] = a[begin2++];}while (begin1 <= end1)tmp[j++] = a[begin1++];while (begin2 <= end2)tmp[j++] = a[begin2++];memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;//while结束后把间隔调两倍}free(tmp);
}
(3)时间复杂度
for循环每次gap*=2,时间复杂度为O(log₂N),for循环中遍历了一遍数组,时间复杂度为O(N)
总的时间复杂度为O(N * log₂N)
(4)空间复杂度
申请了堆上的n个空间,空间复杂度为O(N)
12、非比较排序
(1)基本思想
计数排序是一种非比较排序,实现过程中不需要任何的比较
第一步:统计相同元素出现的次数
第二步:根据统计的结果将序列回收到原来的序列当中
这个排序适用于数据比较集中的序列
(2)代码实现
void CountSort(int* a, int n)
{int min, max;min = max = a[0];for (int i = 0; i < n; i++){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}int range = max - min + 1;//找到这一组数据中最大和最小的数相减得出这组数据的范围int* countA = (int*)malloc(sizeof(int) * range);memset(countA, 0, sizeof(int)*range);//创建一个在堆上的数组作为计数数组,大小为这组数据的范围,将其中的元素全部重置为0for (int i = 0; i < n; i++)countA[a[i] - min]++;//将每个数字出现的次数记录int k = 0;for (int i = 0; i < range; i++){while (countA[i]--)a[k++] = i + min;}
}//下标加上整个数组的最小值就是当前数据的大小,countA为0时退出循环,不为0就记录下来
(3)时间复杂度
找出最大最小值需要遍历一遍数组,记录数字走for循环中range
所以时间复杂度为O(N+range),当数据比较集中时,时间复杂度接近O(N)
到底是O(N)还是O(range)取决于它们俩哪个大
(4)空间复杂度
在堆上开辟了range个空间,空间复杂度为O(range),当数据比较集中时,空间复杂度接近O(1)
三、各个排序方法所用时间的比较
1、代码实现
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();//取随机值a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];//赋值给所有数据}int begin1 = clock();InsertSort(a1, N);int end1 = clock();
//clock是一个函数,用于记录当前时间点,在开始时记录一下,在结束后记录一下
//得出的时间差就是这个排序所用的时间int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();BubbleSort(a3, N);int end3 = clock();int begin4 = clock();SelectSort(a4, N);int end4 = clock();int begin5 = clock();HeapSort(a5, N);int end5 = clock();int begin6 = clock();QuickSort(a6, 0, N - 1);int end6 = clock();int begin7 = clock();MergeSort(a7, N);int end7 = clock();int begin8 = clock();CountSort(a8, N);int end8 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("BubbleSort:%d\n", end3 - begin3);printf("SelcetSort:%d\n", end4 - begin4);printf("HeapSort:%d\n", end5 - begin5);printf("QuickSort:%d\n", end6 - begin6);printf("MergeSort:%d\n", end7 - begin7);printf("CountSort:%d\n", end8 - begin8);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a8);
}
2、分析
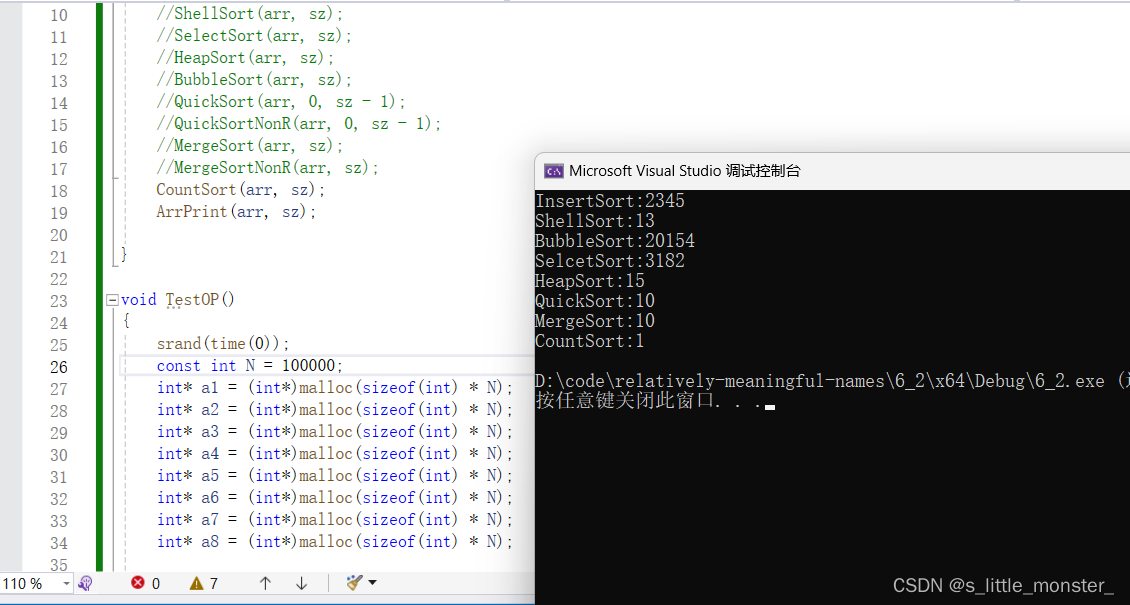
当数据给到10W个时,我们可以明显看出各个排序的差距
最拉胯的就是冒泡排序,跟其他排序所用时间都不在一个量级上
然后就是直接插入以及选择插入
然后就是希尔排序、堆排序、快速排序、归并排序
因为随机数的生成是由时间戳实现的,两个随机数之间差的并不多,所以范围比较集中,这就使得计数排序超级快
四、各个排序的稳定性
1、基本概念
稳定性好就是一个序列中存在着两个即两个以上的相同数据,这两个数据在排序前后相对位置不变,反之就是不好
这里的前后相对位置不变不是指它们两个数据一直待在原来的位置,而是前边的数字a1在排列后还在后边的数字a2前边,而不是跑到它的后边了
2、各个排序的稳定性复杂度一览表
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 简单选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N ^log₂N)~O(N ^2) | O(N^1.3) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N^log₂N) | O(N^log₂N) | O(N^log₂N) | O(1) | 不稳定 |
| 归并排序 | O(N^log₂N) | O(N^log₂N) | O(N^log₂N) | O(N) | 稳定 |
| 快速排序 | O(N^log₂N) | O(N^log₂N) | O(N^2) | O(log₂N)~O(N) | 不稳定 |
感谢观看

相关文章:

【数据结构】排序(下)
个人主页~ 排序(上) 栈和队列 排序 二、常见排序的实现8、快速排序的优化9、非递归快速排序(1)基本思想(2)代码实现(3)时间复杂度(4)空间复杂度 10、归并排序…...
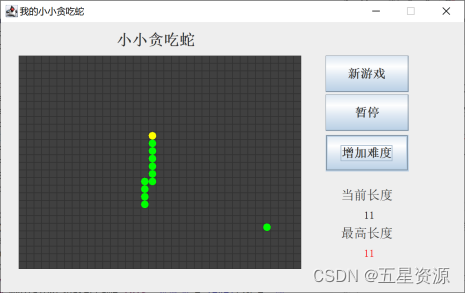
基于Java+Swing贪吃蛇小游戏(含课程报告)
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

三角形法恢复空间点深度
三角形法恢复空间点深度 如下图,以图 I 1 I_1 I1为参考,图 I 2 I_2 I2的变换矩阵为 T T T。相机光心为 O 1 O_1 O1和 O 2 O_2 O2。在图 I 1 I_1 I1中有特征点 p 1 p_1 p1,对应图 I 2 I_2 I2中有特征点 p 2 p_2 p2。理论上直…...

Linux 阻塞和非阻塞 IO 实验学习
Linux 阻塞和非阻塞 IO 实验学习 IO 指的是 Input/Output,也就是输入/输出,是应用程序对驱动设备的输入/输出操作。当应用程序对设备驱动进行操作的时候,如果不能获取到设备资源,那么阻塞式 IO 就会将应用程序对应的线程挂起&…...

JuiceFS 社区版 v1.2 发布,新增企业级权限管理、平滑升级功能
JuiceFS 社区版 v1.2 今天正式发布,这是自 2021 年开源以来的第三个大版本。v1.2 也是一个长期支持版本(LTS)。我们将持续维护 v1.2 以及 v1.1 这两个版本,v1.0 将停止更新。 JuiceFS 是为云环境设计的分布式文件系统,…...

虚拟3D沉浸式展会编辑平台降低了线上办展的门槛
在数字化浪潮的引领下,VR虚拟网上展会正逐渐成为企业展示品牌实力、吸引潜在客户的首选平台。我们与广交会携手走过三年多的时光,凭借优质的服务和丰富的经验,赢得了客户的广泛赞誉。 面对传统展会活动繁多、企业运营繁忙的挑战,许…...

泛微E9开发 查询页面添加按钮,完成特定功能
查询页面添加按钮,完成特定功能 1、关联知识(查询页面实现新增按钮)2、功能实现2.1. 点击按钮,输出选中的checkbox的值2.2. 点击按钮,打开一个自定义对话框 3、实现方法 1、关联知识(查询页面实现新增按钮&…...
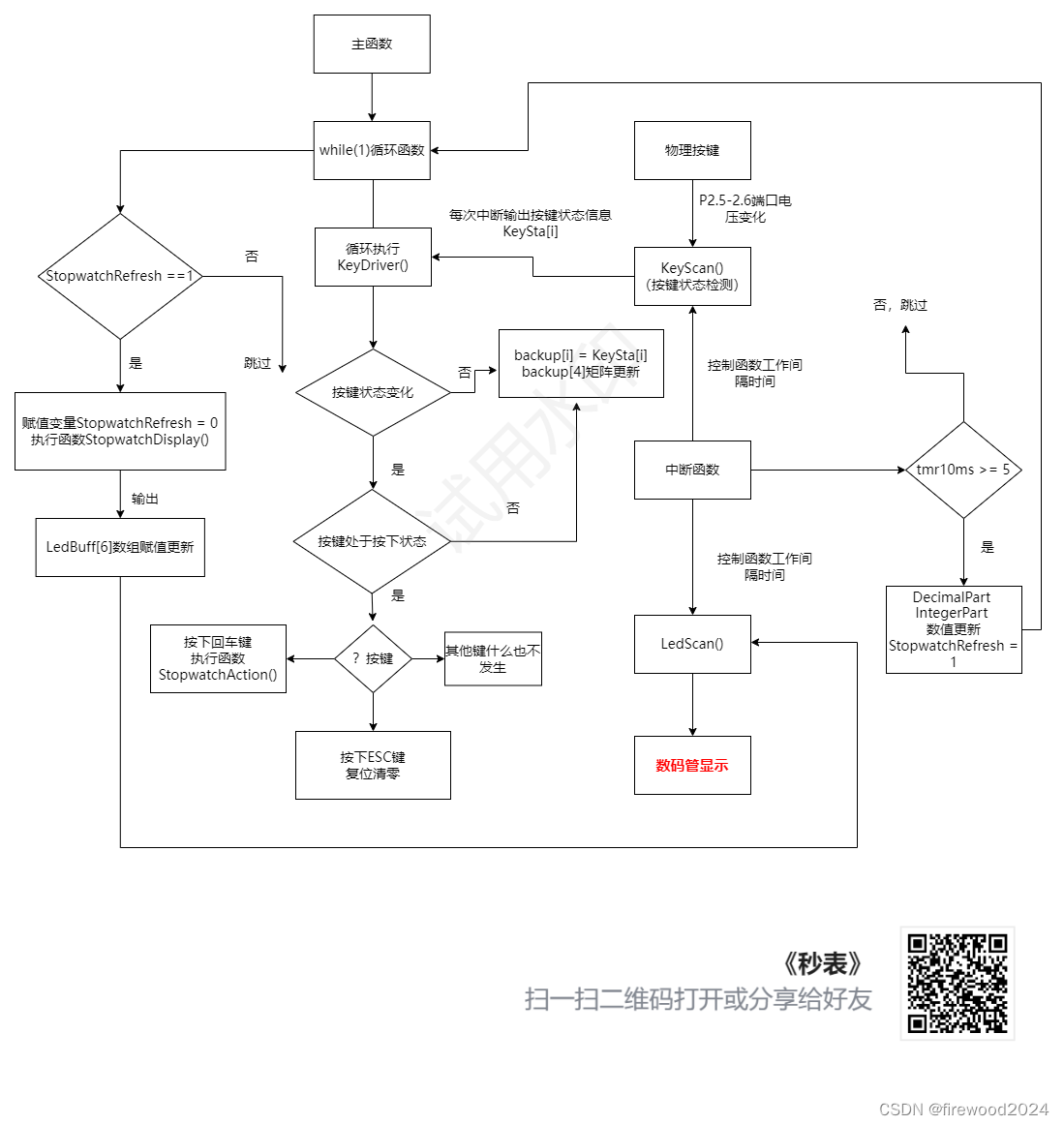
初学51单片机之数字秒表
不同数据类型间的相互转换 在C语言中,不同数据类型之间是可以混合运算的。当表达式中的数据类型不一致时,首先转换为同一类型,然后再进行计算。C语言有两种方式实现类型转换。一是自动类型转换,另外一种是强制类型转换。 转换的主…...
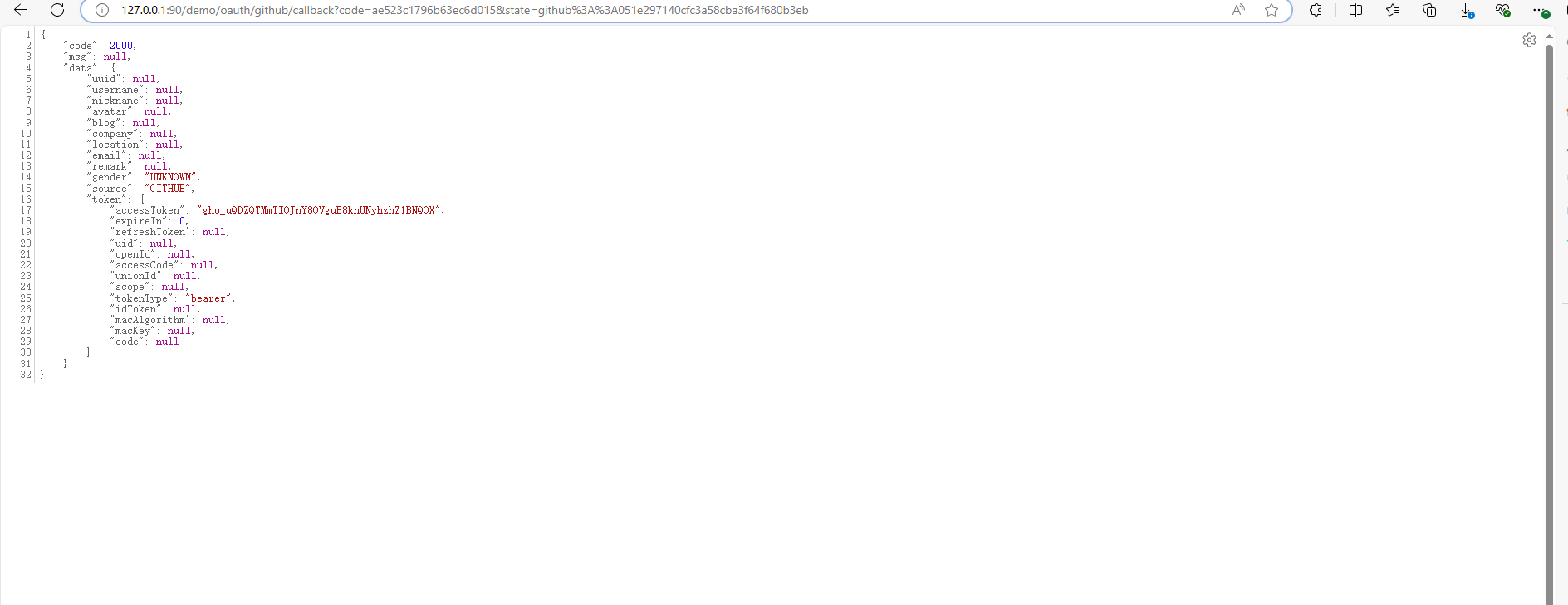
SpringBoot整合justauth实现多种方式的第三方登陆
目录 0.准备工作 1.引入依赖 2.yml文件 3. Controller代码 4.效果 参考 0.准备工作 你需要获取三方登陆的client-id和client-secret 以github为例 申请地址:Sign in to GitHub GitHub 1.引入依赖 <?xml version"1.0" encoding"UTF-8&quo…...

【Java算法】滑动窗口
🔥个人主页: 中草药 🔥专栏:【算法工作坊】算法实战揭秘 👖一. 长度最小的子数组 题目链接:209.长度最小的子数组 算法原理 滑动窗口 滑动窗口算法常用于处理数组/字符串等序列问题,通过定义一…...

C# —— 属性和字段
属性和字段的区别 1.都是定义在一个类中,属于类成员变量 2.字段一般都是私有的private,属性一般是公开的Public 3.字段以小驼峰命名方式 age,属性一般是以大驼峰命名 Age 4.字段可以存储数据,属性不能存储数据,通过属性…...

【计算机视觉】人脸算法之图像处理基础知识(四)
图像的几何变换 图像的几何变换是指在不改变图像内容的前提下对图像的像素进行空间几何变换。主要包括图像的平移变换、镜像变换、缩放和旋转等。 1.插值算法 插值通常用来放缩图像大小,在图像处理中常见的插值算法有最邻近插值法、双线性插值法、二次立方、三次…...

探索 Spring Boot 集成缓存功能的最佳实践
在线工具站 推荐一个程序员在线工具站:程序员常用工具(http://cxytools.com),有时间戳、JSON格式化、文本对比、HASH生成、UUID生成等常用工具,效率加倍嘎嘎好用。 程序员资料站 推荐一个程序员编程资料站:…...

微信小程序使用方法
一.在网页注册小程序账号(在未注册的情况下) 1.如果你还没有微信公众平台的账号,请先进入微信公众平台首页,点击 “立即注册” 按钮进行注册。我们选择 “小程序” 即可。 接着填写账号信息,需要注意的是,…...

前后端分离的后台管理系统源码,快速开发OA、CMS网站后台管理、毕业设计项目
那有没有一款软件解-决这种现状呢?答案是肯定的。引入我们的软件——eladmin。 介绍 ELADMIN,一个简单且易上手的 Spring boot 后台管理框架,已发布 Mybatis-Plus 版本,为开发者提供了一个全-面、高-效的解-决方案。 特点 高-效率:前后端完全分离,项目简单可配,内置代码…...

[深度学习]--分类问题的排查错误的流程
原因复现: 原生的.pt 好使, 转化后的 CoreML不好使, 分类有问题。 yolov8 格式的支持情况 Format Argument Suffix CPU GPU 0 PyTorch - .pt True True 1 Tor…...

微信小程序简易录音机
首先先创建一个项目(想必大家都会啦那就直接开干) 首先上html结构 <view class"wx-container"><view id"title">录音机</view><view id"time">{{hours}}:{{minute}}:{{second}}</view>&l…...

Ollama深度探索:AI大模型本地部署的全面教程
目录 引言一、Ollama概述1、定义与定位2、核心功能3、技术优势4、应用场景 二、安装与配置1、系统要求2、安装方法3、配置指南4、启动Ollama服务 四、快速开始1、启动Ollama2、部署运行模型3、REEST API 五、自定义模型1、定制化的必要性2、使用Modelfile定制模型3、参数调整4、…...

文心一言 VS 讯飞星火 VS chatgpt (285)-- 算法导论21.2 4题
四、请给出图 21-3 所示操作序列的一个运行时间的渐近紧确界,假定使用链表表示和加权合并启发式策略。如果要写代码,请用go语言。 文心一言: 图 21-3 没有直接给出,但通常这种操作序列可能与某种数据结构(如并查集或…...
基于springboot实现影院订票系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现影院订票系统演示 摘要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本影院订票系统就是在这样的大环境下诞生,其可以帮助管理者在…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
