数学建模系列(3/4):典型建模方法
目录
引言
1. 回归分析
1.1 线性回归
基本概念
Matlab实现
1.2 多元回归
基本概念
Matlab实现
1.3 非线性回归
基本概念
Matlab实现
2. 时间序列分析
2.1 时间序列的基本概念
2.2 移动平均
基本概念
Matlab实现
2.3 指数平滑
基本概念
Matlab实现
2.4 ARIMA模型
基本概念
Matlab实现
3. 优化模型
3.1 线性规划
基本概念
Matlab实现
3.2 非线性规划
基本概念
Matlab实现
4. 微分方程模型
4.1 常微分方程模型
基本概念
Matlab实现
4.2 偏微分方程模型
基本概念
Matlab实现
4.3 微分方程模型的应用案例
案例:传染病模型
结语
引言
在前两篇文章中,我们已经介绍了数学建模的基础知识和入门方法。本篇文章将深入讲解几种典型的数学建模方法,包括回归分析、时间序列分析、优化模型和微分方程模型。这些方法在实际问题中应用广泛,对于理解和解决复杂系统中的问题至关重要。通过详细的案例分析和Matlab代码示例,帮助读者掌握具体的建模技术。
1. 回归分析
1.1 线性回归
基本概念
线性回归用于建立因变量与一个或多个自变量之间的线性关系模型。模型形式为:

Matlab实现
% 样本数据
X = [1; 2; 3; 4; 5];
Y = [2; 3; 5; 6; 8];% 线性回归模型
X_ = [ones(size(X)), X]; % 增加常数项
beta = (X_' * X_) \ (X_' * Y);% 预测
Y_pred = X_ * beta;% 绘图
scatter(X, Y, 'bo');
hold on;
plot(X, Y_pred, 'r-');
xlabel('X');
ylabel('Y');
title('线性回归示例');
legend('数据点', '回归线');
1.2 多元回归
基本概念
多元回归用于研究因变量与多个自变量之间的关系。模型形式为:
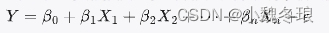
Matlab实现
% 样本数据
X1 = [1; 2; 3; 4; 5];
X2 = [2; 3; 4; 5; 6];
Y = [2; 3; 5; 6; 8];% 多元线性回归模型
X_ = [ones(size(X1)), X1, X2];
beta = (X_' * X_) \ (X_' * Y);% 预测
Y_pred = X_ * beta;% 输出回归系数
disp(['回归系数:', num2str(beta')]);
1.3 非线性回归
基本概念
非线性回归用于拟合非线性关系的模型。常用的非线性模型包括指数模型、对数模型、幂模型等。
Matlab实现
% 样本数据
X = [1; 2; 3; 4; 5];
Y = [2; 4.1; 8.3; 16.2; 32.4];% 非线性模型(幂模型):Y = a * X^b
model_func = @(beta, X) beta(1) * X.^beta(2);
beta0 = [1, 1]; % 初始猜测% 非线性回归
beta = nlinfit(X, Y, model_func, beta0);% 预测
Y_pred = model_func(beta, X);% 绘图
scatter(X, Y, 'bo');
hold on;
plot(X, Y_pred, 'r-');
xlabel('X');
ylabel('Y');
title('非线性回归示例');
legend('数据点', '拟合曲线');
2. 时间序列分析
2.1 时间序列的基本概念
时间序列是按照时间顺序排列的一组数据点,用于描述变量随时间的变化趋势。常见的时间序列分析方法包括移动平均、指数平滑和ARIMA模型。
2.2 移动平均
基本概念
移动平均用于平滑时间序列中的短期波动,识别长期趋势。
Matlab实现
% 样本时间序列数据
data = [22, 24, 25, 23, 26, 28, 27, 29, 30, 31];
window_size = 3; % 移动平均窗口大小% 移动平均
moving_avg = movmean(data, window_size);% 绘图
plot(data, 'b*-');
hold on;
plot(moving_avg, 'r-');
xlabel('时间');
ylabel('值');
title('移动平均示例');
legend('原始数据', '移动平均');
2.3 指数平滑
基本概念
指数平滑用于加强对时间序列中较新的数据点的关注,常见的包括单指数平滑、双指数平滑和三指数平滑。
Matlab实现
% 样本时间序列数据
data = [22, 24, 25, 23, 26, 28, 27, 29, 30, 31];
alpha = 0.2; % 平滑系数% 单指数平滑
exp_smooth = zeros(size(data));
exp_smooth(1) = data(1); % 初始值
for t = 2:length(data)exp_smooth(t) = alpha * data(t) + (1 - alpha) * exp_smooth(t-1);
end% 绘图
plot(data, 'b*-');
hold on;
plot(exp_smooth, 'r-');
xlabel('时间');
ylabel('值');
title('单指数平滑示例');
legend('原始数据', '单指数平滑');
2.4 ARIMA模型
基本概念
ARIMA模型用于捕捉时间序列中的自相关结构,是时间序列分析中最常用的方法之一。
Matlab实现
% 样本时间序列数据
data = [22, 24, 25, 23, 26, 28, 27, 29, 30, 31];% 拟合ARIMA模型
model = arima('Constant', 0, 'D', 1, 'Seasonality', 0, 'MALags', 1, 'SMALags', 12);
fit = estimate(model, data');% 预测
forecast_steps = 5;
[Y, YMSE] = forecast(fit, forecast_steps, 'Y0', data');% 绘图
plot([data, Y']);
hold on;
plot(length(data)+1:length(data)+forecast_steps, Y, 'r*-');
xlabel('时间');
ylabel('值');
title('ARIMA模型示例');
legend('原始数据', '预测值');
3. 优化模型
3.1 线性规划
基本概念
线性规划用于求解目标函数在一组线性约束条件下的最大化或最小化问题。
Matlab实现
% 目标函数系数
f = [-1; -1];% 约束矩阵和向量
A = [1, 2; 3, 1];
b = [6; 9];% 下界和上界
lb = [0; 0];
ub = [inf; inf];% 求解线性规划
[x, fval] = linprog(f, A, b, [], [], lb, ub);% 输出结果
disp(['最优解:', num2str(x')]);
disp(['最优值:', num2str(-fval)]);
3.2 非线性规划
基本概念
非线性规划用于求解目标函数和/或约束条件为非线性的优化问题。
Matlab实现
% 目标函数
obj_fun = @(x) x(1)^2 + x(2)^2;% 约束条件
nonlin_con = @(x) deal([], [x(1) + x(2) - 2]);% 初始猜测
x0 = [0.5, 0.5];% 求解非线性规划
options = optimoptions('fmincon', 'Display', 'iter');
[x, fval] = fmincon(obj_fun, x0, [], [], [], [], [], [], nonlin_con, options);% 输出结果
disp(['最优解:', num2str(x)]);
disp(['最优值:', num2str(fval)]);
4. 微分方程模型
4.1 常微分方程模型
基本概念
常微分方程(ODE)用于描述变量随时间变化的动态过程,广泛应用于物理、化学、生物和经济等领域。常用的一阶和二阶微分方程可以分别表示为:

Matlab实现
% 设定初始条件和时间范围
y0 = 1; % 初始值
tspan = [0, 2]; % 时间区间% 定义一阶微分方程
odefun = @(t, y) t * y;% 求解微分方程
[t, y] = ode45(odefun, tspan, y0);% 绘图
plot(t, y, 'b-');
xlabel('时间');
ylabel('y');
title('常微分方程示例');
legend('y(t)');
4.2 偏微分方程模型
基本概念
偏微分方程(PDE)用于描述具有多个独立变量的系统的动态行为,应用于热传导、流体力学、弹性力学等领域。典型的一维热传导方程表示为:

Matlab实现
% 定义空间和时间范围
x = linspace(0, 1, 20);
t = linspace(0, 1, 50);% 定义初始条件
u0 = sin(pi * x);% 设置PDE系数
m = 0;
alpha = 1;
pdefun = @(x,t,u,DuDx) alpha * DuDx;
icfun = @(x) sin(pi * x);
bcfun = @(xl,ul,xr,ur,t) [ul; ur];% 求解PDE
sol = pdepe(m, pdefun, icfun, bcfun, x, t);% 绘图
surf(x, t, sol);
xlabel('位置 x');
ylabel('时间 t');
zlabel('温度 u');
title('一维热传导方程的数值解');
4.3 微分方程模型的应用案例
案例:传染病模型
问题描述:研究一种传染病在一个封闭社区中的传播情况。
构建SIR模型:
SIR模型是一个常用的传染病模型,包含三个变量:易感者(Susceptible),感染者(Infected)和康复者(Recovered)。模型的微分方程为:

Matlab实现:
% 参数设置
beta = 0.3; % 感染率
gamma = 0.1; % 康复率
N = 1000; % 总人口
I0 = 1; % 初始感染者
R0 = 0; % 初始康复者
S0 = N - I0 - R0; % 初始易感者
y0 = [S0, I0, R0]; % 初始条件% 定义SIR模型的微分方程
sir_ode = @(t, y) [-beta * y(1) * y(2) / N;beta * y(1) * y(2) / N - gamma * y(2);gamma * y(2)];% 时间范围
tspan = [0, 160];% 求解微分方程
[t, y] = ode45(sir_ode, tspan, y0);% 绘图
plot(t, y(:, 1), 'b-', t, y(:, 2), 'r-', t, y(:, 3), 'g-');
xlabel('时间 (天)');
ylabel('人数');
title('SIR模型传染病传播模拟');
legend('易感者', '感染者', '康复者');
通过该案例,我们展示了SIR模型的构建和求解方法,读者可以根据实际情况调整参数,进一步探讨传染病传播的动态行为。
结语
在本篇文章中,我们详细介绍了几种典型的数学建模方法,包括回归分析、时间序列分析、优化模型和微分方程模型。通过具体的例子和Matlab代码示例,读者可以更好地理解这些方法的实际应用和实现过程。希望通过这些基础知识,读者能够在实际问题中灵活运用这些建模方法,解决复杂的系统问题。

相关文章:

数学建模系列(3/4):典型建模方法
目录 引言 1. 回归分析 1.1 线性回归 基本概念 Matlab实现 1.2 多元回归 基本概念 Matlab实现 1.3 非线性回归 基本概念 Matlab实现 2. 时间序列分析 2.1 时间序列的基本概念 2.2 移动平均 基本概念 Matlab实现 2.3 指数平滑 基本概念 Matlab实现 2.4 ARIM…...

AI播客下载:Machine Learning Street Talk(AI机器学习)
该频道由 Tim Scarfe 博士、Yannic Kilcher 博士和 Keith Duggar 博士管理。 他们做了出色的工作,对每个节目进行了彻底的研究,并与机器学习行业中一些受过最高教育、最全面的嘉宾进行了双向对话。 每一集都会教授一些新内容,并且提供未经过滤…...
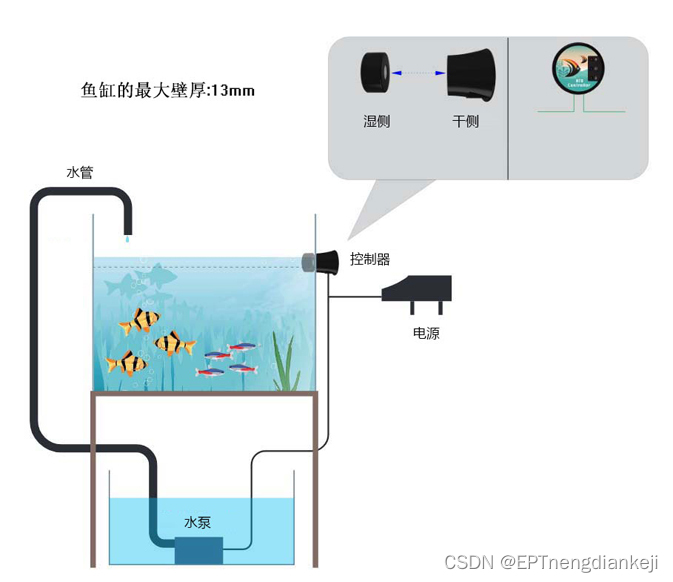
鱼缸补水器工作原理是什么
鱼缸补水器是一种应用广泛的智能设备,主要用于自动监测和补充鱼缸内的水位,以确保鱼类生存环境的稳定。其工作原理简单而高效,为饲主提供了方便和安全的使用体验。 该补水器通常由两部分组成:控制器和吸盘。首先,用户…...

Linux-Tomcat服务配置到系统服务
目录 前言一、系统环境二、配置步骤step1 了解环境的安装路径step2 配置生成tomcat.pid文件step3 配置tomcat.service文件 三、测试systemctl命令管理Tomcat服务3.1 systemctl命令启动Tomcat服务3.2 systemctl命令查看Tomcat服务3.3 systemctl命令关闭Tomcat服务3.4 systemctl命…...

Python抓取高考网图片
Python抓取高考网图片 一、项目介绍二、完整代码一、项目介绍 本次采集的目标是高考网(http://www.gaokao.com/gkpic/)的图片,实现图片自动下载。高考网主页如下图: 爬取的流程包括寻找数据接口,发送请求,解析图片链接,向图片链接发送请求获取数据,最后保存数据。 二…...

Vue配置项data
data 目录 data 目录类型介绍关键原理编译过程 Vue2Vue3 📌Vue.js 中的 data(Obj/Function)属性是 Vue 实例的一个配置选项 类型介绍 对象式 对于根实例或者非复用组件,通常直接提供一个对象字面量作为 data 的值。在对象式中…...
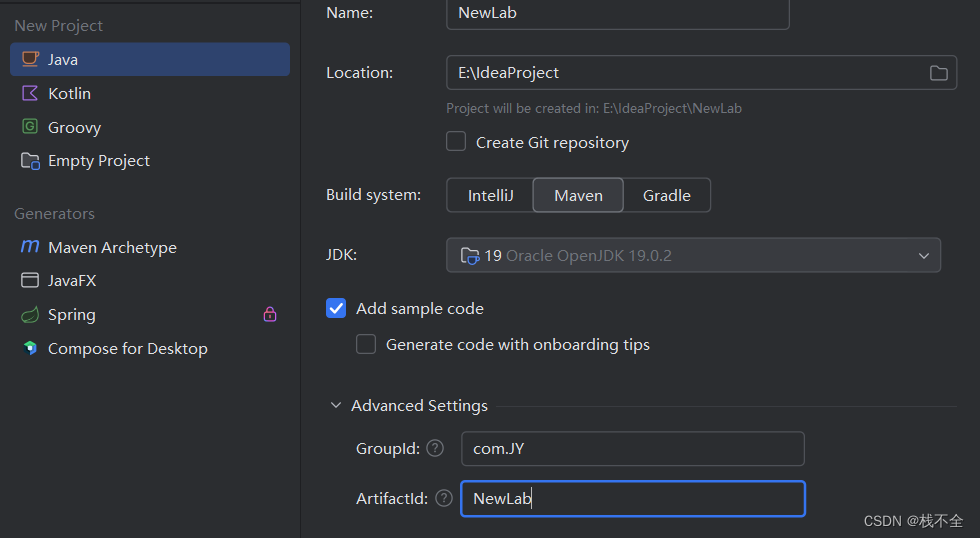
在IDEA 2024.1.3 (Community Edition)中创建Maven项目
本篇博客承继自博客:Windows系统Maven下载安装-CSDN博客 Maven版本:maven-3.9.5 修改设置: 首先先对Idea的Maven依赖进行设置;打开Idea,选择“Costomize”,选择最下边的"All settings" 之后找…...

动手学深度学习(Pytorch版)代码实践 -卷积神经网络-28批量规范化
28批量规范化 """可持续加速深层网络的收敛速度""" import torch from torch import nn import liliPytorch as lp import matplotlib.pyplot as pltdef batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):""&quo…...
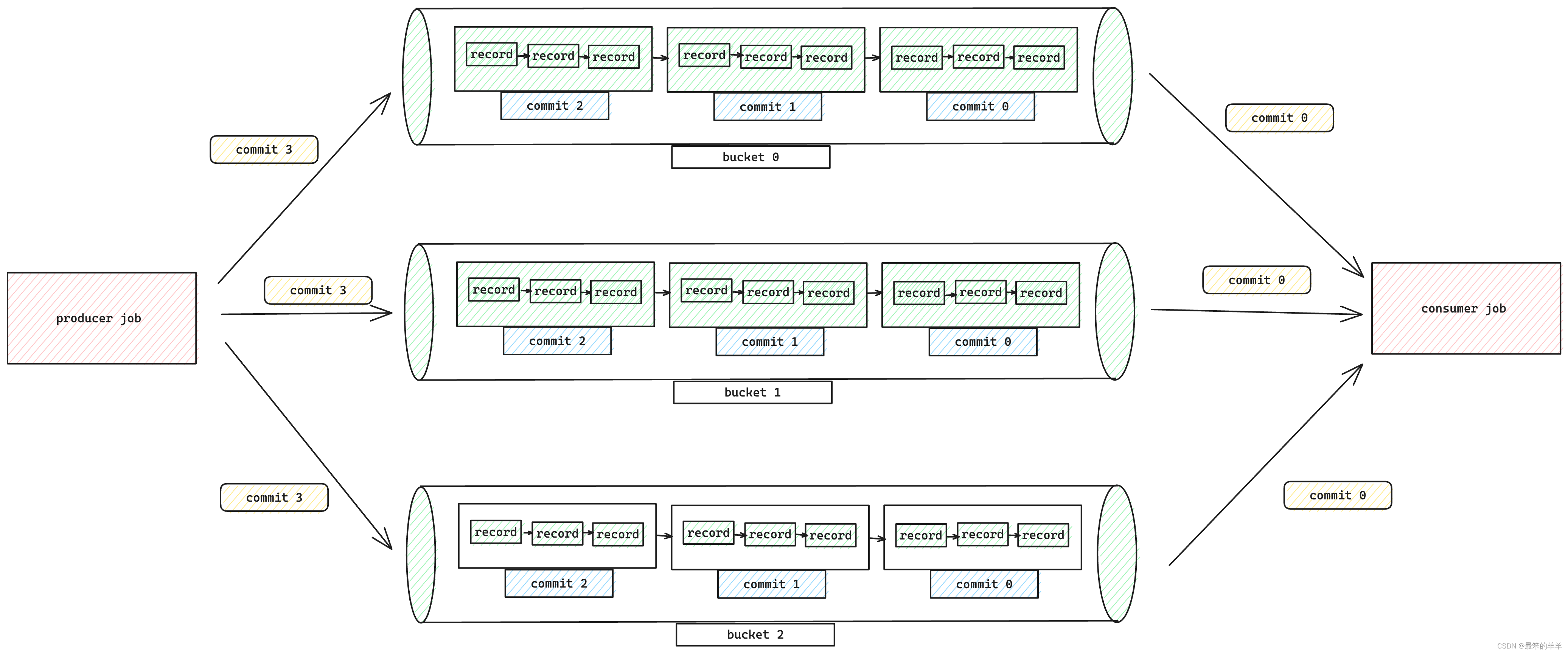
Apache Paimon系列之:Append Table和Append Queue
Apache Paimon系列之:Append Table和Append Queue 一、Append Table二、Data Distribution三、自动小文件合并四、Append Queue五、压缩六、Streaming Source七、Watermark Definition八、Bounded Stream 一、Append Table 如果表没有定义主键,则默认为…...

Vue使用vue-esign实现在线签名 加入水印
Vue在线签名 一、目的二、样式三、代码1、依赖2、代码2.1 在线签名组件2.1.1 基础的2.1.2 携带时间水印的 2.2父组件 一、目的 又来了一个问题,直接让我在线签名(还不能存储base64),并且还得上传,我直接***违禁词。 好…...

与码无关:分数限制下,选好专业还是选好学校?
本文的目标读者:24届的高考生和家长。 写这篇非技术性文章,是因为我看到了24届考生和21年的我同样迷茫。 事先声明,本文带有强烈的个人思考色彩,可能会引起不适,如有不同观点,欢迎在评论区讨论。 一、前言…...

什么是负载均衡技术?
随着网络技术的快速发展,互联网行业也越来越广泛,人们的日常生活中也离不开网络技术,大量的用户进行浏览访问网站时,企业会使用负载均衡技术,降低当前网站的负载,以此来提高网站的访问速度。 今天小编就来给…...

存在重复元素Ⅱ python3
存在重复元素Ⅱ 问题描述解题思路代码实现复杂度 问题描述 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则ÿ…...
【CV炼丹师勇闯力扣训练营 Day13:§6二叉树1】
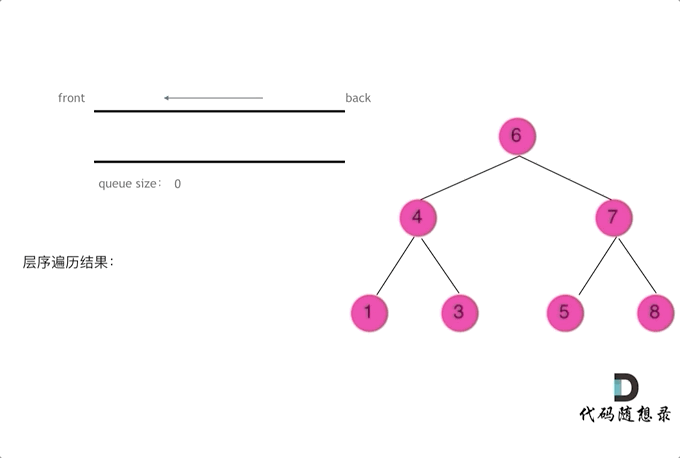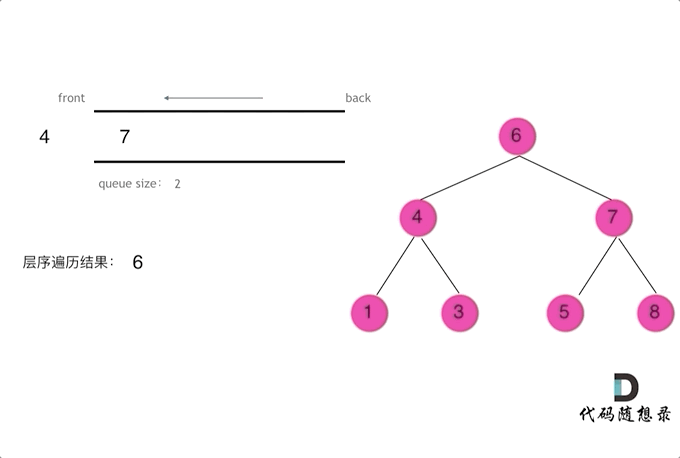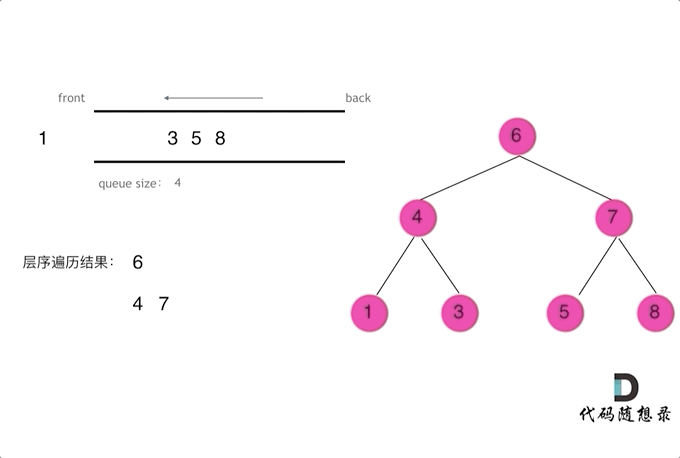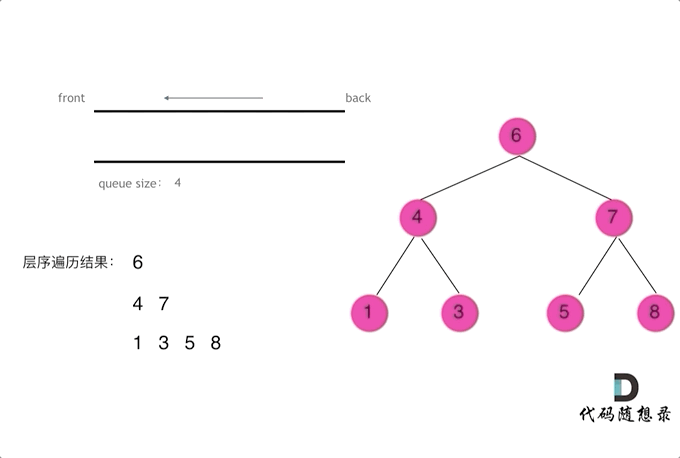
CV炼丹师勇闯力扣训练营 代码随想录算法训练营第13天 二叉树的递归遍历 二叉树的迭代遍历、统一迭代 二叉树的层序遍历 一、二叉树的递归遍历(深度优先搜索) 【递归步骤】 1.确定递归函数的参数和返回值:确定哪些参数是递归的过程中需要处理…...

代码随想录算法训练营第46天 [ 121. 买卖股票的最佳时机 122.买卖股票的最佳时机II 123.买卖股票的最佳时机III ]
代码随想录算法训练营第46天 [ 121. 买卖股票的最佳时机 122.买卖股票的最佳时机II 123.买卖股票的最佳时机III ] 一、121. 买卖股票的最佳时机 链接: 代码随想录. 思路:dp[i][0] 第i天持有股票的最大利润 dp[i][1] 第i天不持有股票的最大利润 做题状态:…...

基于IDEA的Maven简单工程创建及结构分析
目录 一、用 mvn 命令创建项目 二、用 IDEA 的方式来创建 Maven 项目。 (1)首先在 IDEA 下的 Maven 配置要已经确保完成。 (2)第二步去 new 一个 project (创建一个新工程) (3)…...
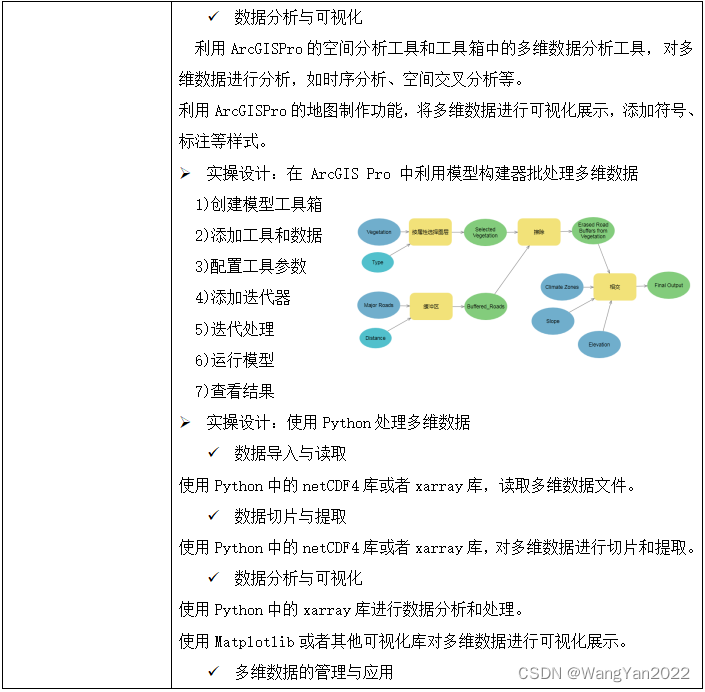
解锁空间数据奥秘:ArcGIS Pro与Python双剑合璧,处理表格数据、矢量数据、栅格数据、点云数据、GPS数据、多维数据以及遥感云平台数据等
ArcGISPro提供了用户友好的图形界面,适合初学者快速上手进行数据处理和分析。它拥有丰富的工具和功能,支持各种数据格式的处理和分析,适用于各种规模的数据处理任务。ArcGISPro在地理信息系统(GIS)领域拥有广泛的应用&…...

后端路线指导(4):后端春招秋招经验分享
后端春招&秋招经验分享 春招(暑期实习) /秋招是应届生非常重要的应聘时间,每一个想就业的同学一定要有所了解! 本篇内容,老白将与大家分享暑期实习和秋招如何应对招聘的个人经验,希望每个同学看完都能有所收获! 首先说明一下老白对于面试核心竞争力的…...

面完小红书算法岗,心态崩了。。。
暑期实习基本结束了,校招即将开启。 不同以往的是,当前职场环境已不再是那个双向奔赴时代了。求职者在变多,HC 在变少,岗位要求还更高了。提前准备才是完全之策。 最近,我们又陆续整理了很多大厂的面试题,…...
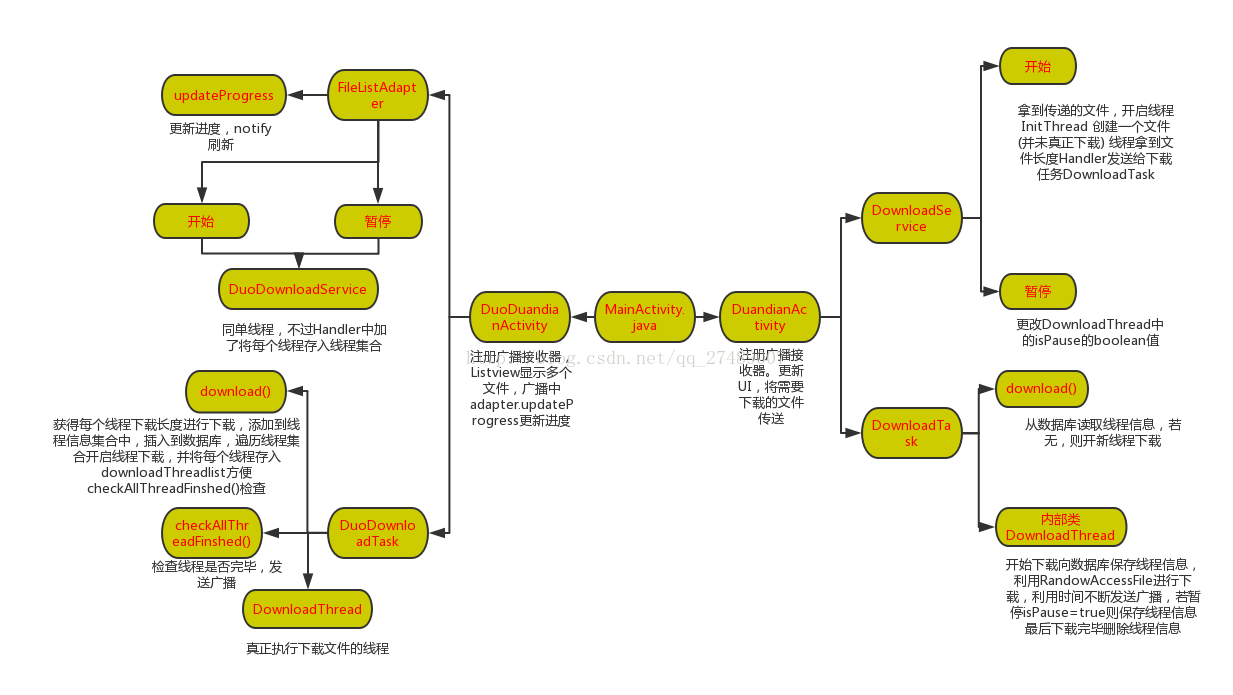
Android 断点续传进阶之多线程下载
今天继续下载的风骚走位内容—多线程多文件断点续传 Android 断点续传基础之单线程下载:http://blog.csdn.net/qq_27489007/article/details/53897653 效果图: 文件关系: 所需内容 多文件下载列表的显示 启动多个线程分段下载 使用通知栏…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...
