VP记录:Codeforces Round 857 (Div. 2) A~D
传送门:CF
A题 Likes:
这道题的题意很变态,十分的难懂,简直就是一坨shit,这场比赛最后被骂是有原因的
简单来说就是对于一个项目,每一个人都能对此加一或者减一,最后问你这个项目每一时刻最大和最小是多少.题目中只说明了只能点赞后才能取消,并没有解释存在取消操作必存在点赞操作(在数据那里悄悄的提了一嘴),但是仍然会造成理解困难
看懂题目之后解决方法很简单,对于最大,我们只要先全部都进行点赞,然后再取消即可
对于最小,我们只要先点赞然后随即取消即可(数据保证取消操作必有一个点赞操作与之对应)
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int T;
vector<int>a,b;
int main() {T=read();while(T--) {int n=read();a.clear();b.clear();for(int i=1;i<=n;i++) {int x=read();if(x>0) a.push_back(x);else b.push_back(x);}int cnt=0;for(int i=0;i<a.size();i++) {printf("%d ",++cnt);}for(int i=0;i<b.size();i++) {printf("%d ",--cnt);}cnt=0;cout<<endl;int pos=0;for(int i=0;i<a.size();i++) {printf("%d ",++cnt);if(pos<b.size()) {printf("%d ",--cnt);pos++;}}while(pos<b.size()) {printf("%d ",--cnt);}cout<<endl;}return 0;
}
B题 Settlement of Guinea Pigs:
题目理解起来也十分的变态,样例也十分的难以理解,只能活该被骂,做起来十分难受
对于每一次查询性别之前,也就是每一个2出现之前记录1的个数,假设我们的1的个数是偶数的话,那么此时我们需要的鸟笼就是(n−2)/2+2(n-2)/2+2(n−2)/2+2,对于我们1的个数是奇数的时候,我们需要的鸟笼的数量就是n/2+1n/2+1n/2+1,接下来来解释一下:
显然我们会发现我们的情况会随着4的余数而进行变化(下面将1,2作为雌雄):
当我们是4的倍数的时候,最坏情况是1,2,1,2…11,12.也就是说对于最后的四个猪,我们的情况并不是1,2,1,2,而应该是11,12,这样才是最坏的情况,此时我们的答案就是(n-2)/2+2
当我们是4的倍数余1时,此时最坏情况是1,2,1,2…1,2,1,2,1,也就是说此时的情况就是n/2+1
当我们是4的倍数余2时,此时最坏的情况是1,2,1,2…1,2,1,2,1,2,此时也还是(n-2)/2+2
当我们是4的倍数余3时,此时最坏的情况是1,2,1,2,…1,2,1,2,1,此时也还是n.2+1
并且注意本题有一个坑点就是在中途过程中我们可能需要很多个鸟笼,虽然可能这些鸟笼在最后可能是空的,但是为了安放好猪,我们依旧需要购买,所以我们需要记录过程中的最大值而不是直接查询最终结果!!
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int main() {int T=read();while(T--) {int n=read();int sum1=0,sum2=0;int ans=0;for(int i=1;i<=n;i++) {int x=read();if(x==1) sum1++;else {if(sum1==0) continue;if(sum1&1) {sum2+=sum1/2;sum1=1;}else {sum2+=(sum1-2)/2;sum1=2;}}ans=max(ans,sum1+sum2);}cout<<ans<<endl;}return 0;
}
C题 The Very Beautiful Blanket:
本题的题面还是比较简明易懂的,做起来的感觉比前两题要爽
由于是一道构造题,所以假设想不到构造的那一个点上本题做起来还是比较痛苦的
我们需要保证每4*4的区间就要满足左上2*2异或和要等于右下2*2异或和,如何保证我们这个做法比较舒服呢.要知道CF上对于这种构造题肯定不会很麻烦的,所以我们大胆猜测,能不能直接保证异或和都等于0呢,这样我们就可以轻易的保证满足题目条件了.而且等于0这个值也比较特殊,大概率是突破口.
那么此时我们就需要保证每2*2的矩阵异或和等于即可,考虑从0开始填矩阵,我们先填满矩阵的第一行,0,1,2,3,4,....m−10,1,2,3,4,....m-10,1,2,3,4,....m−1,因为我们需要保证最后的异或和等于0,那么就意味着我们的第二行的两个数字必须包括上一行的二进制位.我们不妨对于第一行的数字加上一个只有首位的值.例如对于0,10,10,1来说,我们第二行构造出1000+0,1000+11000+0,1000+11000+0,1000+1,这样的话就可以满足异或和等于0了.对于每一个左右相邻数字,我们异或出来最终剩下的就是第一行相邻的数字,再于上下相邻异或,最终都是0
但是此时我们加上这一个二进制位必须比原数字的最高位高才行也就是不能破坏原来的第一行的数字.此时我们第一行数字最大也就是200,所以此时我们采用282^828即可
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int T;
int a[maxn];
int main() {T=read();while(T--) {int n=read(),m=read();cout<<n*m<<endl;for(int i=1;i<=m;i++) {a[i]=i-1;printf("%d ",a[i]);}printf("\n");for(int i=2;i<=n;i++) {for(int j=1;j<=m;j++) {a[j]+=pow(2,8);printf("%d ",a[j]);}printf("\n");}}return 0;
}
D题: Buying gifts
本题题意也比较清明.理解题意十分简单.
对于本题,n的范围为500000,不难感觉应该是一个nlognnlognnlogn算法
考虑对数对<ai,bi>按照ai的大小从小到大进行排序
我们可以考虑枚举A组最大的数字.那么对于A组后面的所有数对,因为当前我们最大值是Ai,所以对于Ai后面的所有数对我们肯定都是选择Bi.对于Ai前面的数对我们可以随意选择,
此时我们的目的是需要max(b)-ai最小.那么对于iii后面的所有bj来说,此时我们可以记录后缀最大值来轻松的找出最大值.那么此时我们只需要找到前缀最大值即可.对于iii前面的所有数对我们进行分类讨论
因为不知道我们的bi的最大值是不是大于ai,所以我们需要找到iii前面所有bjbjbj中恰好大于和小于aiaiai的数,该操作使用setsetset进行,setsetset可以轻松进行插入和二分查找操作
如果存在比ai大的数字,那么此时我们将其后面的最大值进行比较,因为最终的答案需要选出最大的那个数减去ai,我们后面的所有数字又是必选的,所以假如后面的数字比较大,我们此时答案只能是是后面最大值减去ai(选更大的肯定更不优),反之我们选择考虑选择前面的那么查询出来的值.因为此时的值更为贴近我们的ai.(注意此时我们只是选了一下,因为存在一种可能就是后面的最大值才是最贴近的,所以在最后还需要比较一下)
如果存在比ai小的数字,我们的讨论方法类似,此处就不再赘述了
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int T;
vector<pair<int,int> >v;
set<int>se;
int per_mx[maxn];
int main() {T=read();while(T--) {int n=read();v.clear();se.clear();for(int i=0;i<=n+1;i++) {per_mx[i]=0;}for(int i=1;i<=n;i++) {int a=read(),b=read();v.push_back({a,b});}sort(v.begin(),v.end());for(int i=n-1;i>=0;i--) {if(i==n-1) per_mx[i]=v[i].second;else per_mx[i]=max(per_mx[i+1],v[i].second);}int ans=int_INF;for(int i=0;i<=n-1;i++) {int c=int_INF;auto pos=se.lower_bound(v[i].first);if(pos!=se.end()) {if(per_mx[i+1]>=*pos) {c=min(c,abs(v[i].first-per_mx[i+1]));}else {c=min(c,abs(v[i].first-*pos));}}if(pos!=se.begin()) {pos--;if(per_mx[i+1]>=*pos) {c=min(c,abs(v[i].first-per_mx[i+1]));}else {c=min(c,abs(v[i].first-*pos));}}if(i!=n-1) c=min(c,abs(v[i].first-per_mx[i+1]));se.insert(v[i].second);ans=min(ans,c);}cout<<ans<<endl;}return 0;
}
相关文章:
 A~D)
VP记录:Codeforces Round 857 (Div. 2) A~D
传送门:CF A题 Likes: 这道题的题意很变态,十分的难懂,简直就是一坨shit,这场比赛最后被骂是有原因的 简单来说就是对于一个项目,每一个人都能对此加一或者减一,最后问你这个项目每一时刻最大和最小是多少.题目中只说明了只能点赞后才能取消,并没有解释存在取消操作必存在点…...
Docker常用项目实战演练
docker镜像源的修改 linux环境下编辑 /etc/docker/daemon.json vi /etc/docker/daemon.json #如添加如下网易镜像源 { "registry-mirrors": ["http://hub-mirror.c.163.com"] }docker run命令详细解释 日常工作中用的比较多的是docker run命令ÿ…...

Linux进程间通信-FIFO命名管道
Linux进程间通信-FIFO命名管道 1、概述 管道因为没有名称,所以只用于进程间的亲缘通信。为了克服这一缺点,提出了命名管道(FIFO),又称命名管道、FIFO文件。 FIFO不同于无名管道,它提供与之关联的路径名,该路径名以FIF…...

【Kafka】记录一次基于connect-mirror-maker做的Kafka集群迁移完整过程
文章目录背景环境工具选型实操MM1MM2以MM2集群运行以Standalone模式运行验证附录MM2配置表其他背景 一个测试环境的kafka集群,Topic有360,Partition有2000,部署在虚拟机上,由于多方面原因,要求迁移至k8s容器内&#x…...

实现VOC数据集与COCO数据集格式转换
实现VOC数据集与COCO数据集格式转换2、将voc数据集的xml转化为coco数据集的json格式2、COCO格式的json文件转化为VOC格式的xml文件3、将 txt 文件转换为 Pascal VOC 的 XML 格式<annotation><folder>文件夹目录</folder><filename>图片名.jpg</file…...

常用的密码算法有哪些?
我们将密码算法分为两大类。 对称密码(密钥密码)——算法只有一个密钥。如果多个参与者都知道该密钥,该密钥 也称为共享密钥。非对称密码(公钥密码)——参与者对密钥的可见性是非对称的。例如,一些参与者仅…...
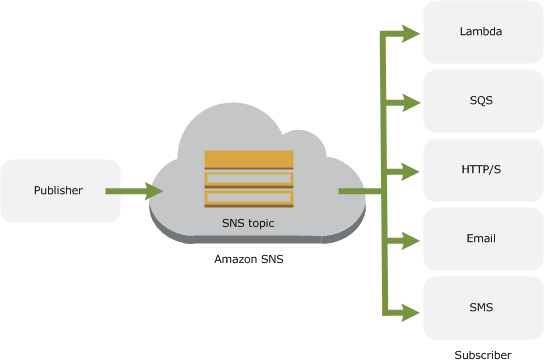
SNS (Simple Notification Service)简介
SNS (Simple Notification Service) 是一种完全托管的发布/订阅消息收发和移动通知服务,用于协调向订阅终端节点和客户端的消息分发。 和SQS (Simple Queue Service)一样,SNS也可以轻松分离和扩展微服务,分布式系统和无服务应用程序…...

JVM初步理解浅析
一、JVM的位置 JVM的位置 JVM在操作系统的上一层,是运行在操作系统上的。JRE是运行环境,而JVM是包含在JRE中 二、JVM体系结构 垃圾回收主要在方法区和堆,所以”JVM调优“大部分也是发生在方法区和堆中 可以说调优就是发生在堆中…...

【巨人的肩膀】MySQL面试总结(一)
💪 目录💪1、什么是ER图2、数据库范式了解吗3、超键、候选键、主键、外键分别是什么?4、为什么不推荐使用外键与级联5、什么是存储过程6、drop、delete与truncate区别7、数据库设计通常分为那几步8、什么是关系型数据库9、什么是SQL10、MySQL…...
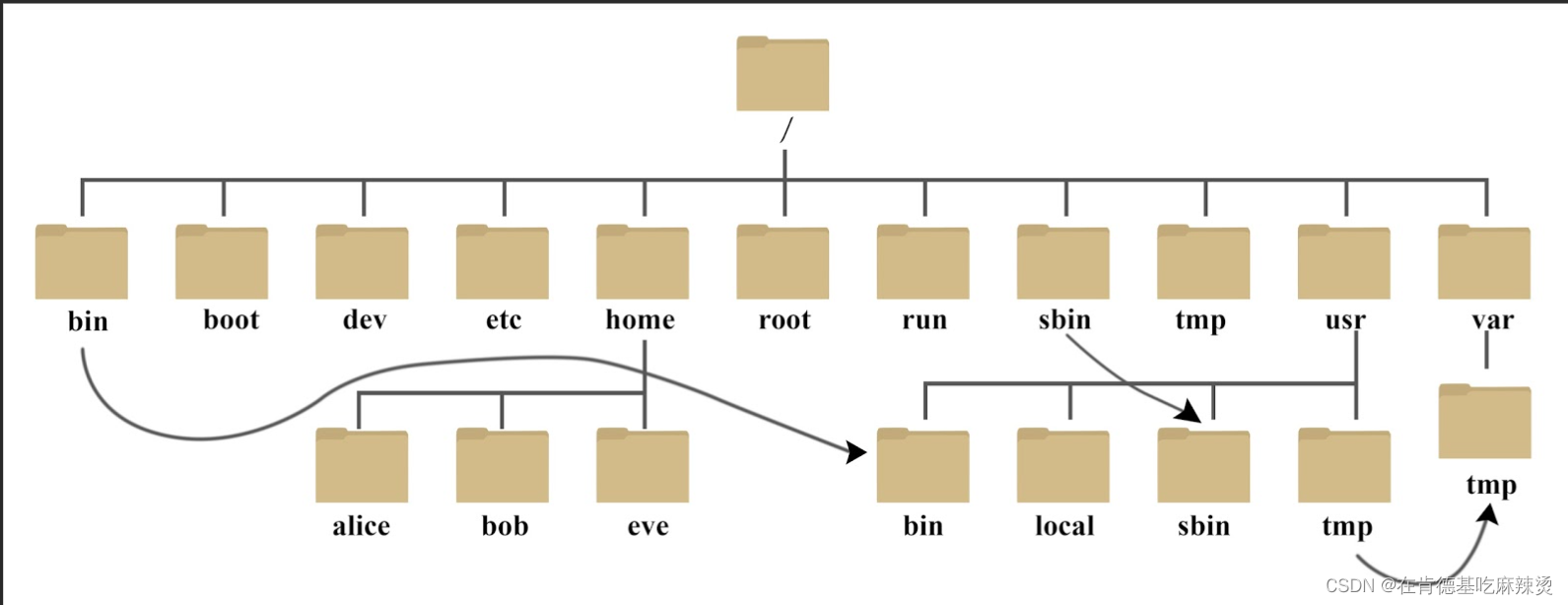
【数据结构之树】——什么是树,树的特点,树的相关概念和表示方法以及在实际的应用。
文章目录一、1.树是什么?2.树的特点二、树的相关概念三、树的表示方法1.常规方法表示树2.使用左孩子右兄弟表示法3. 使用顺序表来存储父亲节点的下标三、树在实际的应用总结一、1.树是什么? 树是一种非线性的数据结构,它是由n(n&…...
JavaScript语法
文章目录一、JavaScript是什么?JavaScript引入方式二、基础语法书写语法输出语句变量数据类型运算符流程控制语句数组函数JS变量作用域对象一、JavaScript是什么? JavaScript:是一门跨平台的脚本语言,用来控制网页行为࿰…...

【BIOS/UEFI】HII 基本框架及概述
HII(Human Interface Infrastructure )定义了一套管理用户输入的基础框架。HII数据库主要提供用户安装、卸载以及使用各种字符串、字体和图片等资源的接口。 HID Devices 是用户输入设备,如键盘、串口和网络;Display Devices 是输…...
溢出边界导致程序崩溃的问题)
sprintf(...)溢出边界导致程序崩溃的问题
文章目录小结问题及解决参考小结 使用sprintf(...)进行格式化是一种标准的做法,但是这样做是有一个极大的风险,由于sprintf(...)不进行边界检查,这样会有写操作溢出边界的风险,并导致程序崩溃。本文进行了简单写操作溢出边界的测…...

公式推导+dfs简版
写在前面的话:心可以冷,但手不能停 第一题:C. Flexible String 题目大意:给一个aaa字符串和bbb字符串和数字kkk,首先设置一个计数器cntcntcnt,其中可以对aaa字符串做以下操作:替换aaa中的一个字母xxx&#…...

论文笔记 | 标准误聚类问题
关于标准误的选择,如是否选择稳健性标准误、是否采取聚类标准误。之前一直是困惑的,惯用的做法是类似主题的文献做法。所以这一次,借计量经济学课程之故,较深入学习了标准误的选择问题。 在开始之前推荐一个知乎博主。他阅读了很…...
银行管理系统--课后程序(Python程序开发案例教程-黑马程序员编著-第7章-课后作业)
实例1:银行管理系统 从早期的钱庄到现如今的银行,金融行业在不断地变革;随着科技的发展、计算机的普及,计算机技术在金融行业得到了广泛的应用。银行管理系统是一个集开户、查询、取款、存款、转账、锁定、解锁、退出等一系列的功…...
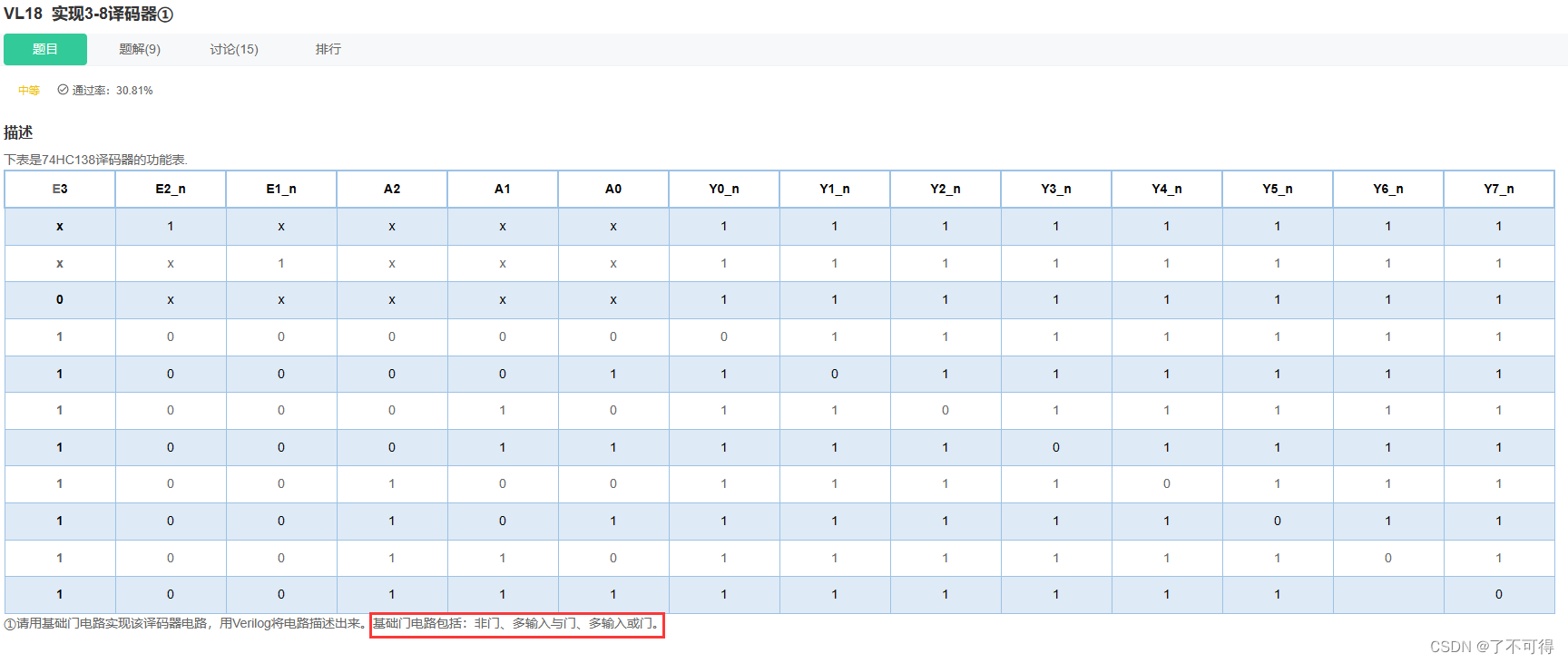
【18】组合逻辑 - VL18 实现3-8译码器①
VL18 实现3-8译码器① 1 题目 【这题我的思路非常绝境】奈斯 !! 看真值表的思路:Yi所在列【0仅一个其余全1】,故【以0为对象求解】 观察发现:E3 E2_n E1_n = 100 时 是 译码的使能信号 ; 并且E3 E2_n E1_n为其他值时,都不使能译码 然后就很简单,没有仿真就成功了 2 代…...

2020蓝桥杯真题最长递增 C语言/C++
题目描述 在数列a_1 ,a_2,⋯,a_n 中,如果a_i <a_i1 <a_i2<⋯<a_j,则称 a_i至 a_j为一段递增序列,长度为 j−i1。 定一个数列,请问数列中最长的递增序列有多长。 输入描述 输入的第一行包含一个整数 n。 第二行包含…...
| 机考必刷)
华为OD机试题 - 寻找连续区间(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:寻找连续区间题目输入输出示例一输入输出说明示例二输入输出Cod…...

一次疲惫的调试--累了及时透气
原创 射频清茶 深山小老虎 2023-03-11 14:32发表于广东 收录于合集 #射频调试3个 #网分4个 #Wi-Fi 2个 进来透透气 道不尽红尘舍恋 诉不完人间恩怨 世世代代都是缘 喝着相同的水 留着相同的血 这条路漫漫又长远 红花当然配绿叶 这一辈子谁来陪 渺渺茫茫来又回 往日情景再…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
