(考研湖科大教书匠计算机网络)第四章网络层-第三节1:IPv4地址概述
- 获取pdf:密码7281
- 专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航
文章目录
- 一:IPv4地址概述
- 二:IPv4地址表示方法
- (1)概述
- (2)8位无符号二进制数转十进制正整数
- (3)十进制正整数转8位无符号二进制数
本节对应视频如下
- 【计算机网络微课堂(有字幕无背景音乐版)】:IPv4地址概述
一:IPv4地址概述
IPv4地址:就是给以太网上的每一台主机(或路由器)的每一个接口分配一个在全世界范围内唯一的32比特的标识符。IP地址由因特网名字和数字分配机构(ICANN)进行分配
- 我国用户可向 亚太网络信息中心(APNIC) 申请IP地址,需要缴费。
- 2011年2月3日,互联网号码分配管理局IANA (由ICANN行使职能)宣布,IPv4地址已经分配完毕
- 我国在2014至2015年也逐步停止了向新用户和应用分配IPv4地址。同时全面开展商用部署IPv6
IPv4地址的编址方法经历了如下三个历史阶段
- 分类编址(1981)
- 划分子网(1985)
- 无分类编址(1993)
二:IPv4地址表示方法
(1)概述
IPv4地址表示方法:由于32比特的IPv4地址不方便阅读、记录以及输入等,因此IPv4地址采用点分十进制表示方法以方便用户使用
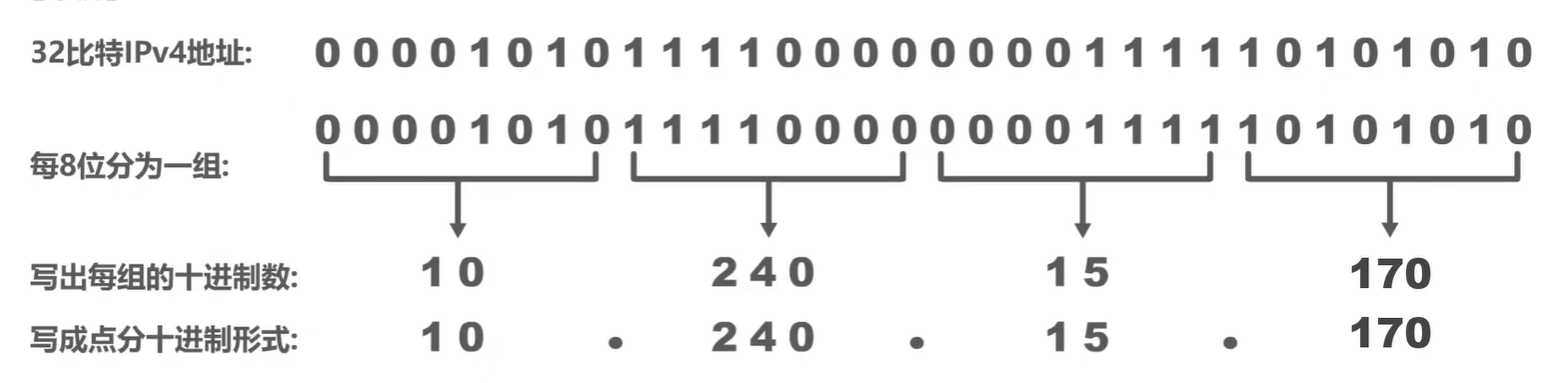
(2)8位无符号二进制数转十进制正整数
- 更多有关进制转换问题可见:(计算机组成原理)第二章数据的表示和运算-第一节1:进位计数及进制转换
二进制数的每个位权值为
| 2102^{10}210 | 292^{9}29 | 282^{8}28 | 272^{7}27 | 262^{6}26 | 252^{5}25 | 242^{4}24 | 232^{3}23 | 222^{2}22 | 212^{1}21 | 202^{0}20 | 2−12^{-1}2−1 | 2−22^{-2}2−2 | 2−32^{-3}2−3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
8位无符号二进制整数转为十进制整数方法如下:
(b7b6b5b4b3b2b1b0)2=(b7×27+b6×26+b5×25+b4×24+b3×23+b2×22+b1×21+b0×20)10(b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0})_{2}=(b_{7}×2^{7}+b_{6}×2^{6}+b_{5}×2^{5}+b_{4}×2^{4}+b_{3}×2^{3}+b_{2}×2^{2}+b_{1}×2^{1}+b_{0}×2^{0})_{10} (b7b6b5b4b3b2b1b0)2=(b7×27+b6×26+b5×25+b4×24+b3×23+b2×22+b1×21+b0×20)10
举例:
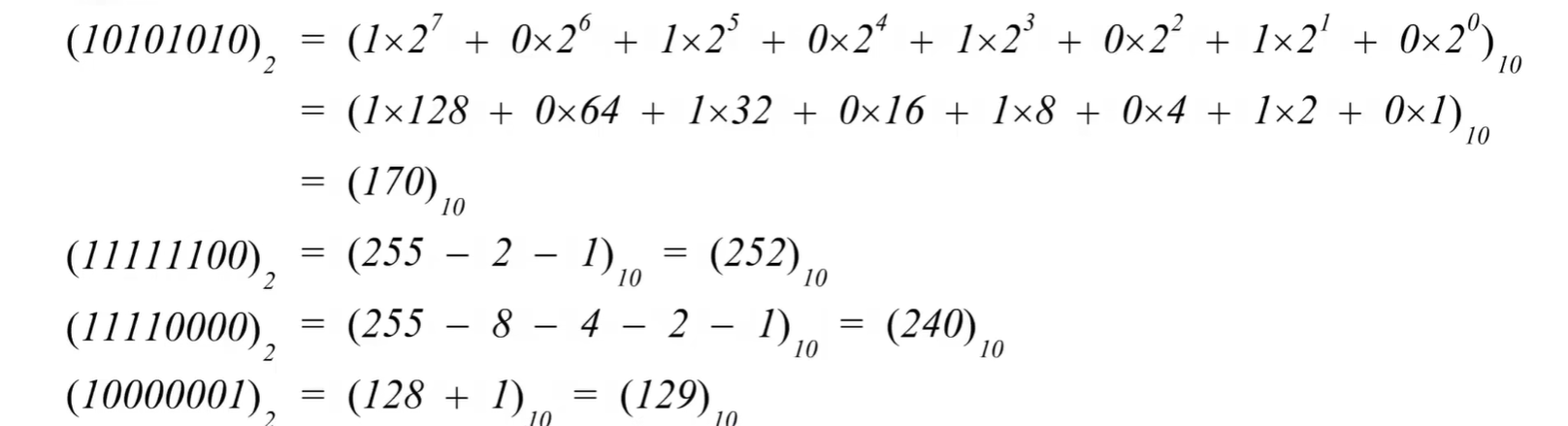
(3)十进制正整数转8位无符号二进制数
基本方法:除2取余法

快速方法:凑值法
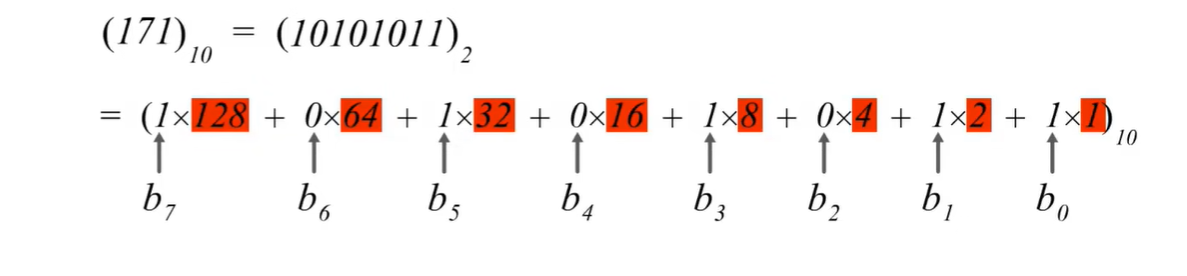
相关文章:
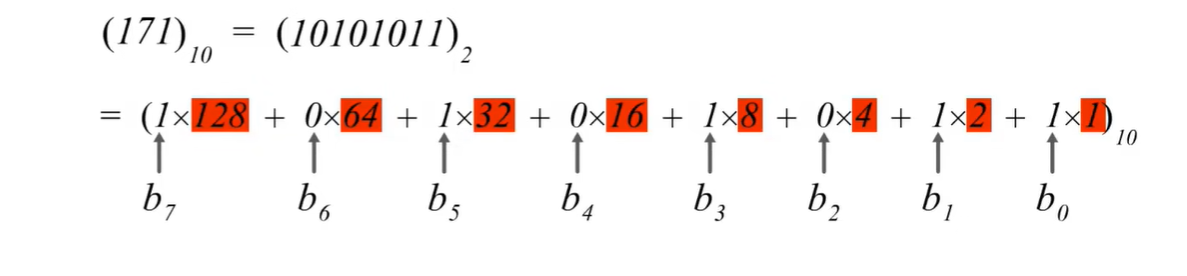
(考研湖科大教书匠计算机网络)第四章网络层-第三节1:IPv4地址概述
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:IPv4地址概述二:IPv4地址表示方法(1)概述(2)8位无符号二进制数转十进制正整数ÿ…...

B站Python与OpenCV人脸识别项目超详细记录(对图片、视频、摄像头人脸的检测)
课程来源:一天搞定人脸识别项目!学不会up直接下跪!(pythonopencv)_哔哩哔哩_bilibili 图片来源:感谢王鹤棣先生友情出镜~ 环境配置详见: 在conda虚拟环境中安装OpenCv并在pycharm中使用_cond…...

【Node.js实战】一文带你开发博客项目之Koa2重构(实现session、开发路由、联调、日志)
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,也会涉及到服务端 📃个人状态: 在校大学生一枚,已拿多个前端 offer(秋招) 🚀未…...
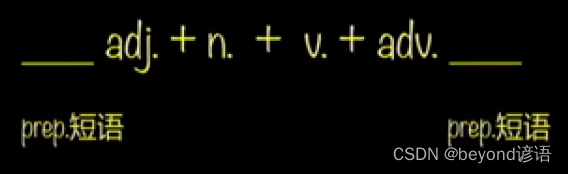
第一部分:简单句——第二章:简单句的补充
简单句的核心构成:一主一谓 主语/宾语/表语 可以变成名词/代词/doing/to do 谓语动词有四种核心变化:三态 一否 时态语态情态否定 简单句的核心:将简单句给写对 简单句的补充:将简单句给写的更好、更充分 简单句的补充 1、限定…...

Spring Security简介
前面我们已经完成了传智健康后台管理系统的部分功能,例如检查项管理、检查组管理、套餐管理、预 约设置等。接下来我们需要思考2个问题: 问题1:在生产环境下我们如果不登录后台系统就可以完成这些功能操作吗? 答案显然是否定的&am…...
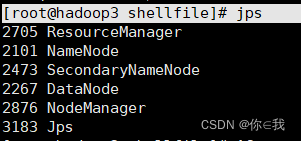
Hadoop安装 --- 简易安装Hadoop
目录 1、使用xftp工具 在opt目录下创建install和soft文件 2、使用xftp工具 将压缩包上传到install文件 3、编写shell脚本 3.1、创建目录来放shell脚本 3.2、创建autoinsatll.sh文件并修改权限 3.3、编写autoinsatll.sh 文件 刷新资源 运行文件 格式化 启动所有进程 Ha…...

俞军产品方法论,消化吸收,要点整理
一、总体概括二、产品经理、价值、用户模型、交易模型三、价值、产品和企业的价值生存游戏的常见要点:企业做产品的4方面产出:四、决策五、俞军产品方法论,认知迭代史1)俞军12条产品军规2)产品经理职级的背后影响因素:…...

spring注解的开端(@Component替代bean标签的使用)
目录 一、介绍 1.什么是注解开发? 2.Spring注解的版本 3.基于spring注解的应用 4. Component的细分注解 5.相关注解 二、简单例子讲解 1.类打注解 2.扫描注解放入工厂 3.总工厂取注解调用 4.运行结果 总结: 一、介绍 1.什么是注解开发&…...
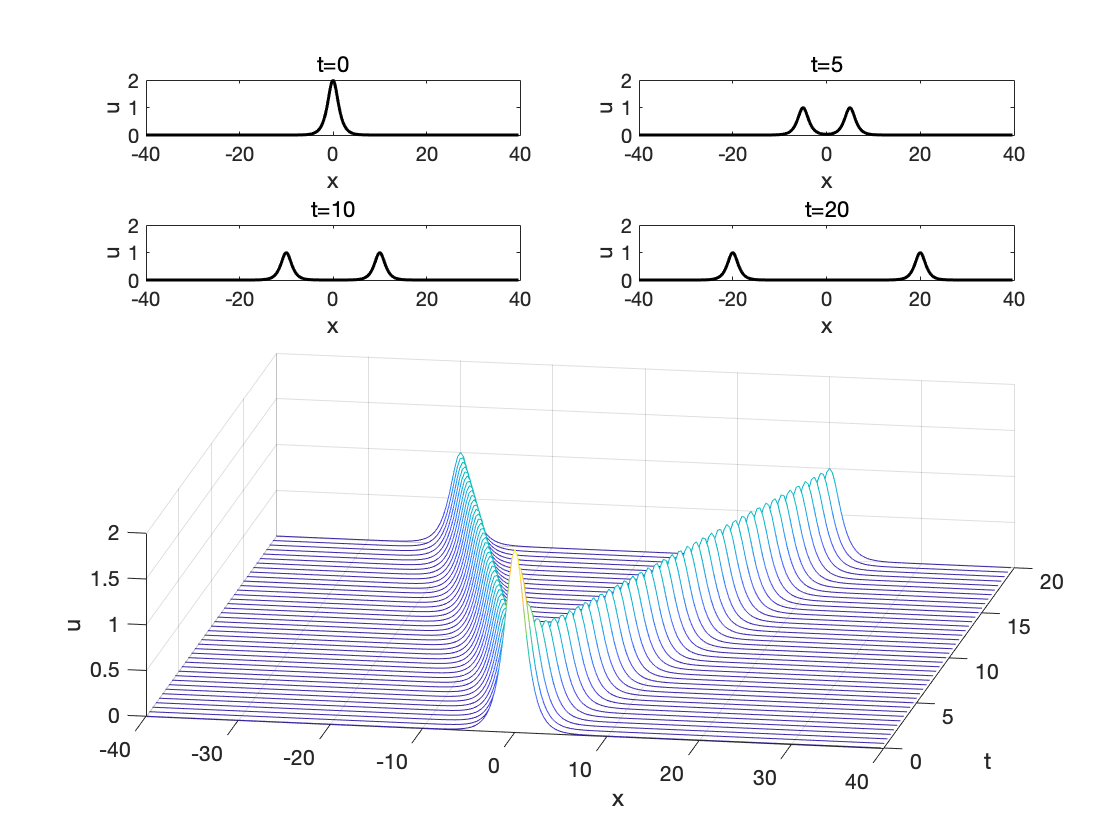
Matlab傅里叶谱方法求解一维波动方程
傅里叶谱方法求解基本偏微分方程—一维波动方程 一维波动方程 对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间 里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 (−∞<x<∞)(-\infty<x&…...
函数典型例题)
py3中 collections.Counter()函数典型例题
文章目录py3中 collections 的常用STL**Counter()** 函数**defaultdict()** 函数**deque()** 函数**orderedDict()** 函数(缺例题)小结py3中 collections 的常用STL 对于这个工具包非常好用,尤其是其中的 Counter() 函数 使用次数颇为频繁&a…...

Linux部署达梦数据库超详细教程
陈老老老板🦸👨💻本文专栏:国产数据库-达梦数据库👨💻本文简述:本文讲一下达梦数据库的下载与安装教程(Linux版),超级详细。👨💻…...

ctfshow 每周大挑战 极限命令执行
《简单的命令执行题目》 这里感叹一下,g4佬是真好厉害,这次题目十分的难,嗯,对我这种菜鸡来说是这样的,想了一天,最后结束了,也还是没有想明白第五题的解法,我真是fw,到最…...

使用vue3,vite,less,flask,python从零开始学习硅谷外卖(16-40集)
严正声明! 重要的事情说一遍,本文章仅供分享,文章和代码都是开源的,严禁以此牟利,严禁侵犯尚硅谷原作视频的任何权益,我知道学习编程的人各种各样的心思都有,但这不是你对开源社区侵权的理由&am…...

坚持就是胜利
很多朋友,可能坚持了多年的同等学力申硕考试,依然没有通过。如果你感到困惑,感到迷茫,要坚信:坚持就能胜利。有很多人跟你一样,一直坚持在路上,没有停止脚步。 生活没有你想象的那么好ÿ…...
 或者转置 intrinsic (内参)矩阵的原因)
代码中出现转置 pose (c2w,外参矩阵) 或者转置 intrinsic (内参)矩阵的原因
在代码中见到 pose(c2w),intrinsic 矩阵的转置,觉得比较奇怪。 后来想了一下为什么。下面解释一下: 用 c2w 矩阵举例子。理论上,一个 c2w 左乘上 一个相机坐标系下的点 P的坐标,能够得到该点在…...

2023 年腾讯云服务器配置价格表出炉(2核2G/2核4G/4核8G/8核16G、16核32G)
腾讯云轻量应用服务器为轻量级的云服务器,使用门槛低,按套餐形式购买,轻量应用服务器套餐自带的公网带宽较大,4M、6M、7M、10M、14M及20M套餐可选,如果是云服务器CVM这个带宽价格就要贵很多了。 1、轻量应用服务器优惠…...
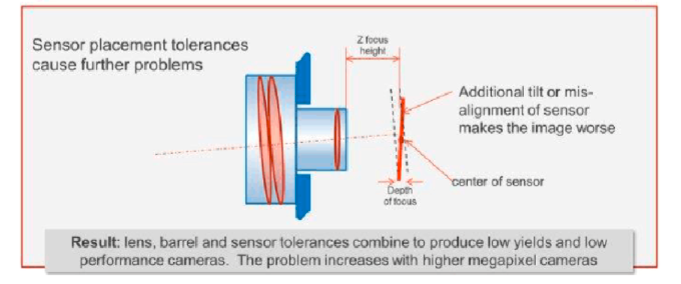
相机出图画面一半清晰,一半模糊的原因是什么?
1、问题背景:在做项目的过程中,有遇到过几次,出图后画面是一半清晰,一半模糊的现象,再重新对焦也是一样。但换了个镜头后就好了,这应该是镜头的质量问题,但导致镜头出现这种问题的具体原因是什么…...
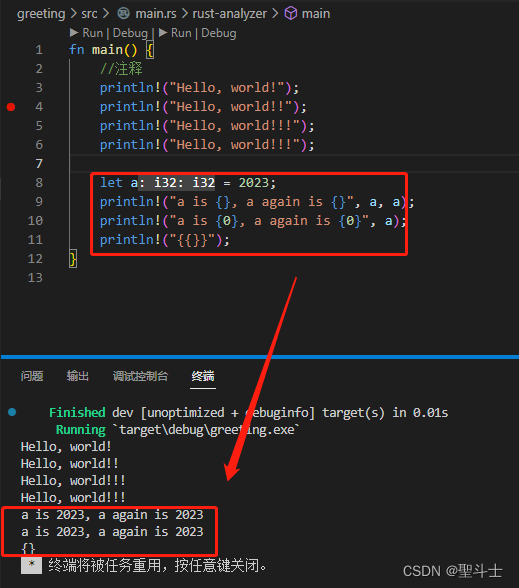
Rust学习入门--【4】Rust 输出到命令行
Rust 语言中的打印“函数” 学习新的编程语言时,大家都喜欢打印“Hello World”。 在Rust中怎样将字符串打印出来呢? Rust 输出文字的方式主要有两种:println!() 和 print!()。 “函数”差异说明: 这两个"函数"都是向…...

Vector刷写方案—vFlash工具介绍
我是穿拖鞋的汉子,魔都中坚持长期主义的工科男! 今天魔都天气是连阴雨,滴滴答答的下个不停,心情也跟着潮湿起来!老规矩分享一段喜欢的文字,避免成为高知识低文化的工程师: 即使在真正的困境里,也一直提示自己,每次自恋不得超过十分钟! 那些看似无法度过得困境,不是…...
》)
【阶段总结】《非结构化信息分析应用与实践(筹)》
《非结构化信息分析应用与实践(筹)》Part 1.知识储备一、机器学习 1.几种常见的有监督学习算法 2.几种常见的无监督学习算法 3.数据挖掘基础知识 30 问 二、神经网络与深度学习 1.MP神经网络模型(附实例代码讲解) 2.图解LST…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
