详解三种常用标准化 Batch Norm Layer Norm RMSNorm
- 参考:
- BN究竟起了什么作用?一个闭门造车的分析
- 《动手学深度学习》7.5 节
- 深度学习中,归一化是常用的稳定训练的手段,CV 中常用 Batch Norm; Transformer 类模型中常用 layer norm,而 RMSNorm 是近期很流行的 LaMMa 模型使用的标准化方法,它是 Layer Norm 的一个变体
- 值得注意的是,这里所谓的归一化严格讲应该称为
标准化Standardization,它描述一种把样本调整到均值为 0,方差为 1 的缩放平移操作。归一化、标准化、正则化等术语常常被混用,可以看 标准化、归一化概念梳理(附代码) 这篇文章理清 - 详细讨论前,先粗略看一下 Batch Norm 和 Layer Norm 的区别

-
BatchNorm是对整个 batch 样本内的每个特征做归一化,这消除了不同特征之间的大小关系,但是保留了不同样本间的大小关系。BatchNorm 适用于 CV 领域,这时输入尺寸为 b × c × h × w b\times c\times h\times w b×c×h×w (批量大小x通道x长x宽),图像的每个通道 c c c 看作一个特征,BN 可以把各通道特征图的数量级调整到差不多,同时保持不同图片相同通道特征图间的相对大小关系
-
LayerNorm是对每个样本的所有特征做归一化,这消除了不同样本间的大小关系,但是保留了一个样本内不同特征之间的大小关系。LayerNorm 适用于 NLP 领域,这时输入尺寸为 b × l × d b\times l\times d b×l×d (批量大小x序列长度x嵌入维度),如下图所示

注意这时长 l l l 的 token 序列中,每个 token 对应一个长为 d d d 的特征向量,LayerNorm 会对各个 token 执行 l l l 次归一化计算,保留每个 token d d d 维嵌入内部的相对大小关系,同时拉近了不同 token 对应特征向量间的距离。与之相比,BN 会消除 d d d 维特征向量各维度之间的大小关系,破坏了 token 的特征(以下第 2 节会进一步说明这一点)
-
文章目录
- 1. Batch Normalization
- 2. Layer Normalization
- 3. RMSNorm
1. Batch Normalization
-
BN 对同一 batch 内同一通道的所有数据进行归一化,设输入的 batch data 为 x \pmb{x} x,BN 运算如下
B N ( x ) = γ ⊙ x − μ ^ B σ ^ B + β . \mathrm{BN}(\mathbf{x})=\boldsymbol{\gamma} \odot \frac{\mathbf{x}-\hat{\boldsymbol{\mu}}_{\mathcal{B}}}{\hat{\boldsymbol{\sigma}}_{\mathcal{B}}}+\boldsymbol{\beta} . BN(x)=γ⊙σ^Bx−μ^B+β. 其中 ⊙ \odot ⊙ 表示按位置乘, γ \pmb{\gamma} γ 和 β \pmb{\beta} β 是拉伸参数scale和偏移参数shift,这两个参数的 size 和特征维数相同,代表着把第 i i i 个特征的 batch 分布的均值和方差移动到 β i , γ i \beta^i, \gamma^i βi,γi, γ \pmb{\gamma} γ 和 β \pmb{\beta} β 是需要与其他模型参数一起学习的参数。 μ ^ B \hat{\boldsymbol{\mu}}_{\mathcal{B}} μ^B 和 σ ^ B \hat{\boldsymbol{\sigma}}_{\mathcal{B}} σ^B 表示 batch data 中各特征的均值和方差,如下计算
μ ^ B = 1 ∣ B ∣ ∑ x ∈ B x σ ^ B 2 = 1 ∣ B ∣ ∑ x ∈ B ( x − μ ^ B ) 2 + ϵ \begin{aligned} \hat{\boldsymbol{\mu}}_{\mathcal{B}}&=\frac{1}{|\mathcal{B}|} \sum_{\mathbf{x} \in \mathcal{B}} \mathbf{x} \\ \hat{\boldsymbol{\sigma}}_{\mathcal{B}}^{2}&=\frac{1}{|\mathcal{B}|} \sum_{\mathbf{x} \in \mathcal{B}}\left(\mathbf{x}-\hat{\boldsymbol{\mu}}_{\mathcal{B}}\right)^{2}+\epsilon \end{aligned} μ^Bσ^B2=∣B∣1x∈B∑x=∣B∣1x∈B∑(x−μ^B)2+ϵ 注意我们在方差估计值中添加一个小的常量 ϵ \epsilon ϵ,以确保我们永远不会尝试除以零 -
注意一些细节
-
在 MLP 中应用 BN 时,均值和方差的计算发生在各个特征维度上。此时输入数据形式通常为 x ∈ R b × n \pmb{x}\in\mathbb{R}^{b\times n} x∈Rb×n,其中 b = ∣ B ∣ b=|\mathcal{B}| b=∣B∣ 为 batch size, n n n 为特征维度,有 μ ^ B , σ ^ B 2 , γ , β ∈ R 1 × n \hat{\boldsymbol{\mu}}_{\mathcal{B}},\hat{\boldsymbol{\sigma}}_{\mathcal{B}}^{2},\pmb{\gamma},\pmb{\beta} \in \mathbb{R}^{1\times n} μ^B,σ^B2,γ,β∈R1×n
-
在 CNN 中应用 BN 时,均值和方差的计算发生在各个通道上。此时输入数据形式通常为 x ∈ R b × c × h × w \pmb{x}\in\mathbb{R}^{b\times c\times h\times w} x∈Rb×c×h×w,其中 b = ∣ B ∣ b=|\mathcal{B}| b=∣B∣ 为 batch size, c , h , w c, h, w c,h,w 分别为为通道数量和图像长宽尺寸,有 μ ^ B , σ ^ B 2 , γ , β ∈ R 1 × c × 1 × 1 \hat{\boldsymbol{\mu}}_{\mathcal{B}},\hat{\boldsymbol{\sigma}}_{\mathcal{B}}^{2},\pmb{\gamma},\pmb{\beta} \in \mathbb{R}^{1\times c \times 1\times 1} μ^B,σ^B2,γ,β∈R1×c×1×1,如下图所示

-
BN 层在”训练模式“(通过小批量统计数据规范化)和“预测模式”(通过数据集统计规范化)中的功能不同。 训练过程中,我们无法得知使用整个数据集来估计平均值和方差,所以只能根据每个小批次的平均值和方差不断训练模型;预测模式下,可以根据整个数据集精确计算批量规范化所需的平均值和方差
-
-
BatchNorm是一种在深度学习训练中广泛使用的归一化技术,有很多好处,包括正则化效应、减少过拟合、减少对权重初始值的依赖、允许使用更高的学习率等
- 一方面,BN 使每一层隐藏值分布主动居中,并将它们重新调整为学习到的最佳均值和方差,这种操作可能将参数的量级进行了统一,因此直觉上往往被认为可以使优化更加平滑
- 另一方面,BN 有效性的科学性解释一度存在争议。15 年提出BN的论文声称 BN 减小了所谓的
内部协变量偏移internal covariate shift,因此可以提高模型性能,但其分析中假设了每层隐变量值都服从某种正态分布,这个假设过强了,很多后续研究指出了其问题。18 年的论文 How Does Batch Normalization Help Optimization? 认为 BN 的主要作用是使得整个损失函数的 landscape 更为平滑,从而使得我们可以更平稳地进行训练。相关分析可以参考苏神的博文
-
示例代码参考自《动手学深度学习》7.5 节,适用于全连接层和卷积层,训练过程中使用滑动平均法计算 batch 数据的均值和方差;评估过程中使用最新的均值和方差结果
class BatchNorm(nn.Module):# num_features:完全连接层的输出数量或卷积层的输出通道数。def __init__(self, num_features, num_dims):super().__init__()if num_dims == 2: # 全连接层shape = (1, num_features)else: # 卷积层shape = (1, num_features, 1, 1)# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0self.gamma = nn.Parameter(torch.ones(shape))self.beta = nn.Parameter(torch.zeros(shape))# 非模型参数的变量初始化为0和1self.moving_mean = torch.zeros(shape)self.moving_var = torch.ones(shape)def batch_norm(self, X, gamma, beta, moving_mean, moving_var, eps, momentum):if not torch.is_grad_enabled():# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)else:assert len(X.shape) in (2, 4)if len(X.shape) == 2:# 使用全连接层的情况,计算特征维上的均值和方差mean = X.mean(dim=0) # (num_features,)var = ((X - mean) ** 2).mean(dim=0) # (num_features,)else:# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。mean = X.mean(dim=(0, 2, 3), keepdim=True) # (1,num_features,1,1) 保持X的形状,以便后面可以做广播运算var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True) # (1,num_features,1,1)# 训练模式下,用当前的均值和方差做标准化X_hat = (X - mean) / torch.sqrt(var + eps)# 更新移动平均的均值和方差moving_mean = momentum * moving_mean + (1.0 - momentum) * meanmoving_var = momentum * moving_var + (1.0 - momentum) * varY = gamma * X_hat + beta # 缩放和移位return Y, moving_mean.data, moving_var.datadef forward(self, X):# 如果X不在内存上,将moving_mean和moving_var,复制到X所在显存上if self.moving_mean.device != X.device:self.moving_mean = self.moving_mean.to(X.device)self.moving_var = self.moving_var.to(X.device)# 保存更新过的moving_mean和moving_varY, self.moving_mean, self.moving_var = self.batch_norm(X, self.gamma, self.beta, self.moving_mean,self.moving_var, eps=1e-5, momentum=0.9)return Y
2. Layer Normalization
-
LN 主要用于 NLP 领域,它对每个 token 的特征向量进行归一化计算。设某个 token 的特征向量为 x ∈ R d \pmb{x}\in \mathbb{R}^d x∈Rd,LN 运算如下
L N ( x ) = γ ⊙ x − μ ^ σ ^ + β . \mathrm{LN}(\mathbf{x})=\boldsymbol{\gamma} \odot \frac{\mathbf{x}-\hat{\boldsymbol{\mu}}}{\hat{\boldsymbol{\sigma}}}+\boldsymbol{\beta} . LN(x)=γ⊙σ^x−μ^+β. 其中 ⊙ \odot ⊙ 表示按位置乘, γ , β ∈ R d \pmb{\gamma}, \pmb{\beta}\in \mathbb{R}^d γ,β∈Rd 和 是拉伸参数scale和偏移参数shift,代表着把第 i i i 个特征的 batch 分布的均值和方差移动到 β i , γ i \beta^i, \gamma^i βi,γi, γ \pmb{\gamma} γ 和 β \pmb{\beta} β 是需要与其他模型参数一起学习的参数。 μ ^ \hat{\boldsymbol{\mu}} μ^ 和 σ ^ \hat{\boldsymbol{\sigma}} σ^ 表示特征向量所有元素的均值和方差,如下计算
μ ^ = 1 d ∑ x i ∈ x x i σ ^ 2 = 1 d ∑ x i ∈ x ( x i − μ ^ ) 2 + ϵ \begin{aligned} \hat{\boldsymbol{\mu}}&=\frac{1}{d} \sum_{x^i \in \mathbf{x}} x^i \\ \hat{\boldsymbol{\sigma}}^{2}&=\frac{1}{d} \sum_{x^i \in \mathbf{x}}\left(x^i-\hat{\boldsymbol{\mu}}\right)^{2}+\epsilon \end{aligned} μ^σ^2=d1xi∈x∑xi=d1xi∈x∑(xi−μ^)2+ϵ 注意我们在方差估计值中添加一个小的常量 ϵ \epsilon ϵ,以确保我们永远不会尝试除以零 -
给定一个长 l l l 的句子,LN 要进行 l l l 次归一化计算,之后对每个特征维度施加统一的拉伸和偏移,如下图所示

-
为什么 LN 比 BN 更适用于 Transformer 类模型呢,这是因为 transformer 模型是基于相似度的,把序列中的每个 token 的特征向量进行归一化有利于模型学习语义,第一步调整均值方差时,相当于对把各个 token 的特征向量缩放到统一的尺度,第二步施加 γ , β \pmb{\gamma, \beta} γ,β 时,相当于对所有 token 的特征向量进行了统一的 transfer,这不会破坏 token 特征向量间的相对角度,因此不会破坏学到的语义信息。与之相对的,BN 沿着特征维度进行归一化,这时对序列中各个 token 施加的 transfer 是不同的,破坏了 token 特征向量间的相对角度关系
-
Transformer 类模型中,LayerNorm 层有两种放置方式
Pre Norm: x t + 1 = x t + F t ( Norm ( x t ) ) Post Norm: x t + 1 = Norm ( x t + F t ( x t ) ) \text{Pre Norm:} \quad \boldsymbol{x}_{t+1}=\boldsymbol{x}_{t}+F_{t}\left(\operatorname{Norm}\left(\boldsymbol{x}_{t}\right)\right) \\ \text{Post Norm:} \quad \boldsymbol{x}_{t+1}=\operatorname{Norm}\left(\boldsymbol{x}_{t}+F_{t}\left(\boldsymbol{x}_{t}\right)\right) Pre Norm:xt+1=xt+Ft(Norm(xt))Post Norm:xt+1=Norm(xt+Ft(xt)) 如下图所示

目前比较明确的结论是:同一设置之下,Pre Norm结构往往更容易训练,但最终效果通常不如Post Norm
- Pre Norm 更容易训练好理解,因为它的恒等路径更突出
- Pre Norm 中多层叠加的结果更多是增加宽度而不是深度,层数越多,这个层就越“虚”,这是因为 Pre Norm 结构无形地增加了模型的宽度而降低了模型的深度,而我们知道深度通常比宽度更重要,所以是无形之中的降低深度导致最终效果变差了。而 Post Norm 刚刚相反,它每Norm一次就削弱一次恒等分支的权重,所以 Post Norm 反而是更突出残差分支的,因此Post Norm中的层数更加有分量,起到了作用,一旦训练好之后效果更优。详细说明参考 为什么Pre Norm的效果不如Post Norm?
-
过去 BERT 主流的时代往往使用 Post Norm,现在 GPT 时代模型规模都很大,因此大多用 Pre Norm 来稳定训练
3. RMSNorm
- RMSNorm 是 LayerNorm 的一个简单变体,来自 2019 年的论文 Root Mean Square Layer Normalization,被 T5 和当前流行 lamma 模型所使用。其提出的动机是 LayerNorm 运算量比较大,所提出的RMSNorm 性能和 LayerNorm 相当,但是可以节省7%到64%的运算
- RMSNorm和LayerNorm的主要区别在于RMSNorm不需要同时计算均值和方差两个统计量,而只需要计算均方根 Root Mean Square 这一个统计量,公式如下
RMSNorm ( x ) = γ ⊙ x RMS ( x ) where RMS ( x ) = 1 d ∑ x i ∈ x x i 2 + ϵ \text{RMSNorm}(\pmb{x})=\boldsymbol{\gamma} \odot\frac{\pmb{x}}{\operatorname{RMS}(x)} \quad \text{where \quad}\operatorname{RMS}(x)=\sqrt{\frac{1}{d} \sum_{x^i \in \mathbf{x}} x_{i}^{2} + \epsilon} RMSNorm(x)=γ⊙RMS(x)xwhere RMS(x)=d1xi∈x∑xi2+ϵ - 论文 Do Transformer Modifications Transfer Across Implementations and Applications? 中做了比较充分的对比实验,显示出RMS Norm的优越性。一个直观的猜测是,计算均值所代表的 center 操作类似于全连接层的 bias 项,储存到的是关于预训练任务的一种先验分布信息,而把这种先验分布信息直接储存在模型中,反而可能会导致模型的迁移能力下降
- 下面给出 Transformer Lamma 源码中实现的 RMSNorm
class LlamaRMSNorm(nn.Module):def __init__(self, hidden_size, eps=1e-6):"""LlamaRMSNorm is equivalent to T5LayerNorm"""super().__init__()self.weight = nn.Parameter(torch.ones(hidden_size))self.variance_epsilon = epsdef forward(self, hidden_states):input_dtype = hidden_states.dtypehidden_states = hidden_states.to(torch.float32)variance = hidden_states.pow(2).mean(-1, keepdim=True)hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)return self.weight * hidden_states.to(input_dtype)
相关文章:

详解三种常用标准化 Batch Norm Layer Norm RMSNorm
参考: BN究竟起了什么作用?一个闭门造车的分析《动手学深度学习》7.5 节 深度学习中,归一化是常用的稳定训练的手段,CV 中常用 Batch Norm; Transformer 类模型中常用 layer norm,而 RMSNorm 是近期很流行…...

云计算运维工程师面试
1. 云计算运维工程师的角色和职责是什么? 回答: 云计算运维工程师负责确保云计算环境(包括硬件和软件系统)的高可用性和稳定性。他们的主要职责包括: 监测系统和应用程序的性能,确保它们正常运行。故障排除,快速响应并解决系统或应用程序中出现的问题。容量规划,根据…...

聚观早报 | iPhone 16核心硬件曝光;三星Galaxy全球新品发布会
聚观早报每日整理最值得关注的行业重点事件,帮助大家及时了解最新行业动态,每日读报,就读聚观365资讯简报。 整理丨Cutie 6月28日消息 iPhone 16核心硬件曝光 三星Galaxy全球新品发布会 苹果正多方下注布局AI商店 黄仁勋2024年薪酬3400…...

web前端之文档流、浮动、定位详解
目录 一、文档流 二、浮动 1.添加浮动 2.清除浮动 三、定位 1.相对定位 2.绝对定位 一、文档流 什么是文档流? ● 文档流指的是文档中的标签在排列时所占用的位置。 将窗体自上而下分成一行行 ,并在每 行中按从左至右的顺序排放标签,…...

[JS]节点操作
DOM节点 DOM树中的所有内容都是节点, 我们重点关注元素节点 作用 使开发者可以根据节点的关系获取元素, 而不是只能依赖选择器, 提高了编码的灵活性 节点分类 元素节点: 所有的标签都是元素节点, html是根节点属性节点: 所有的属性都是属性节点, 比如href文本节点: 所有的文…...

基于SpringBoot+Vue的论坛网站系统(带1w+文档)
基于SpringBootVue的论坛网站系统(带1w文档) 对于之前论坛网站的管理,大部分都是使用传统的人工方式去管理,这样导致了管理效率低下、出错频率高。而且,时间一长的话,积累下来的数据信息不容易保存,对于查询、更新还有…...
03逻辑门电路
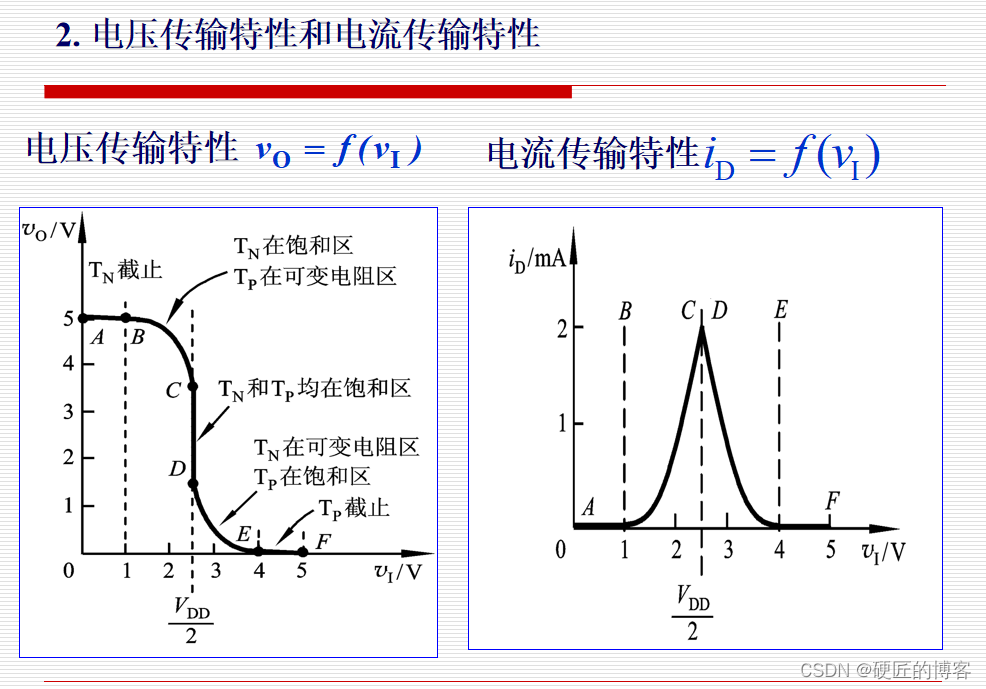
分立门电路: 集成门电路: TTL门电路 MOS门电路:NMOS门电路、PMOS门电路、CMOS门电路 BICMOS门电路:CMOS的高输入阻抗和TTL的高放大倍数的结合 向更低功耗、更高速度发展 MOS管的Rdson在可变电阻区的阻值也一般会小于1000欧姆 …...

2毛钱的SOT23-5封装28V、1.5A、1.2MHz DCDC转换器用于LCD偏置电源和白光LED驱动等MT3540升压芯片
前言 之前发了一个TI的BOOST升压芯片,用于LCD偏置电压或LED驱动,请访问以下链接。 6毛钱SOT-23封装28V、400mA 开关升压转换器,LCD偏置电源和白光LED应用芯片TPS61040 国产半导体厂家发展迅猛,今天推荐一个公司带“航天”的升压…...
Zookeeper部署
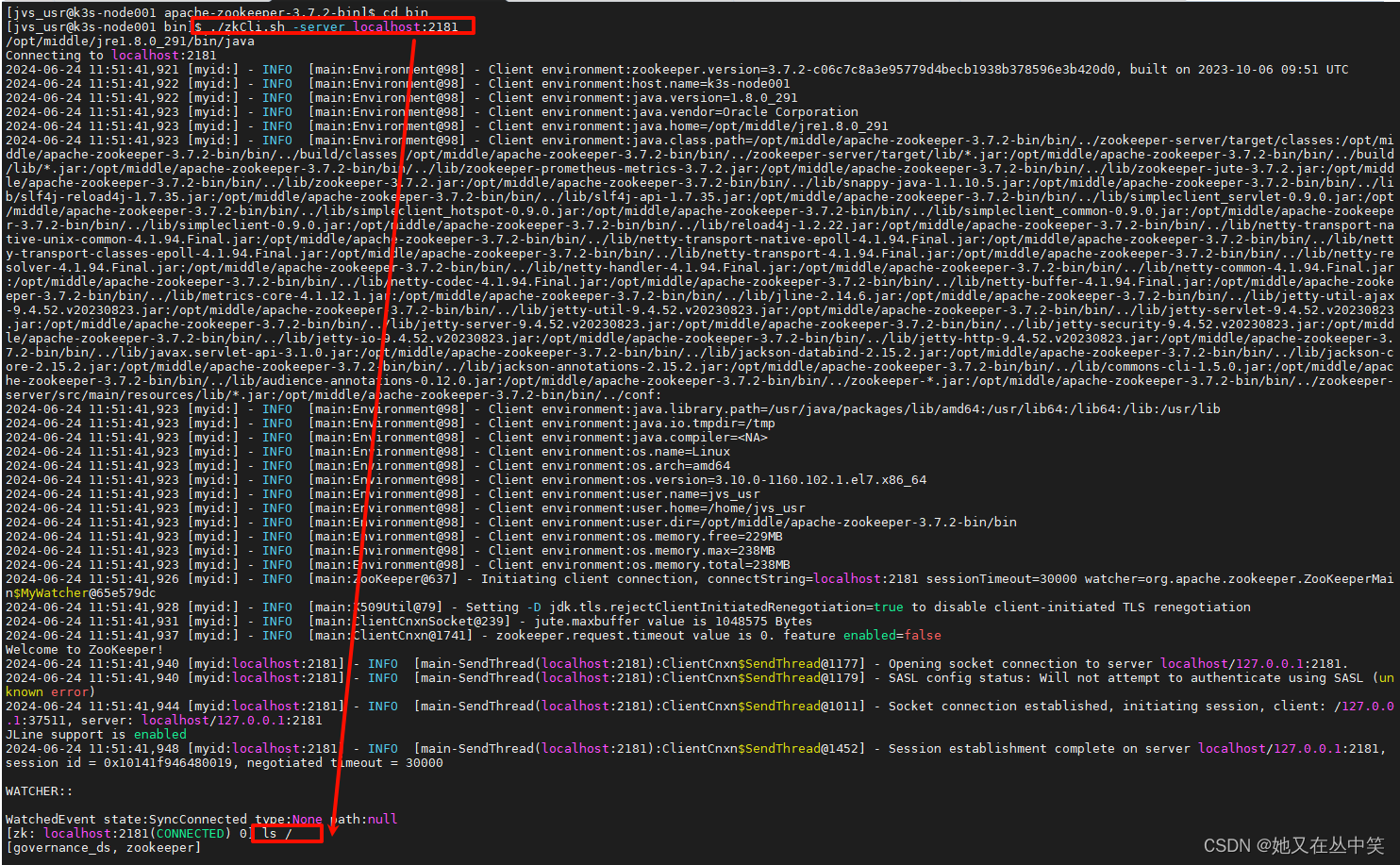
Zookeeper部署 下载安装包Linux解压安装包修改配置文件编辑zoo.cf配置 启动服务停止服务常用zookeeper指令查看namespace列表创建namespace删除namespace 注意:该文章为简单部署操作,没有复杂的配置内容,用的是3.7.2版本。 下载安装包 进入z…...

2.x86游戏实战-跨进程读取血量
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 本次游戏没法给 内容参考于:微尘网络安全 接下来会写C/C代码,C/C代码不是很难,然后为了快速掌握逆向这个技能,我…...
element-plus 日期选择添加确定按钮
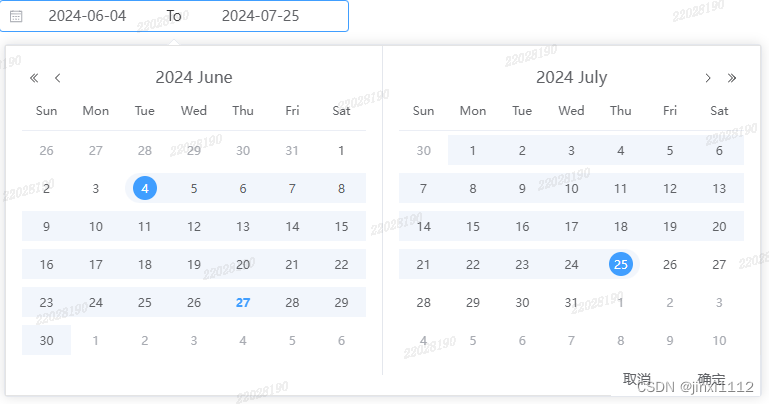
需求:选择日期后,点击确定按钮关闭面板 思路: 使用shortcuts自定义确定和取消按钮选择日期后使用handleOpen()强制开启面板点击确定后使用handleClose()关闭面板 <template><el-date-pickerref"pickerRef"v-model"…...
Redis优化之持久化
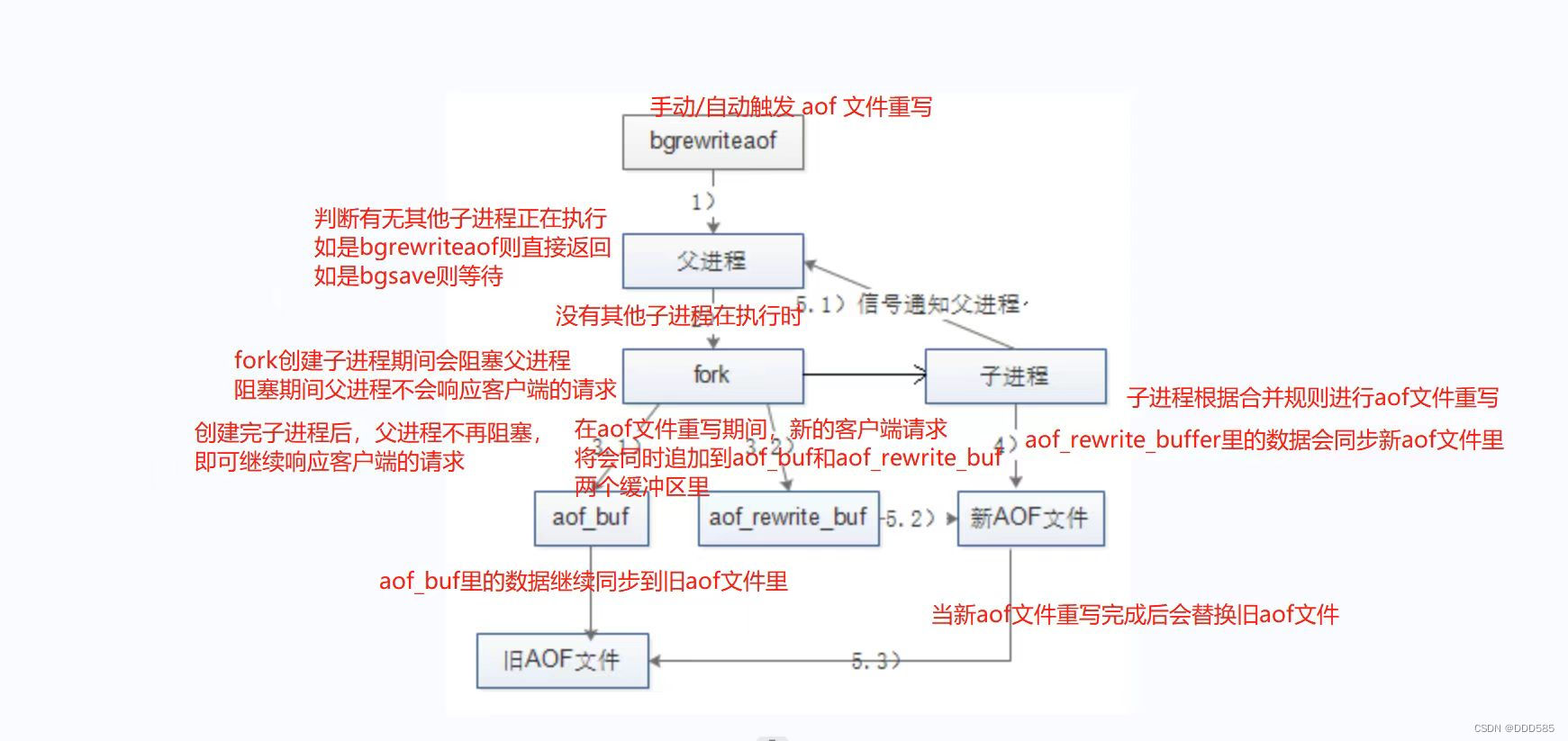
目录 1.Redis高可用 2.Redis持久化 2.1 RDB持久化 2.1.1 触发条件 2.1.2 执行流程 2.1.3 启动时加载 2.2 AOF持久化 2.2.1 开启AOF 2.2.2 执行流程 2.2.3 文件重写触发方式 2.2.4 文件重写的流程 2.2.5 启动时加载 2.3 RDB和AOF的优缺点 3.Redis性能管理 3.1 查看…...

ubuntu22.04 编译安装libcurl C++ library
1. 安装必须的依赖项 sudo apt update #sudo apt install build-essential autoconf libtool pkg-config libssl-dev libz-dev 2. 下载及编译前准备 cd /opt mkdir curl && cd curl mkdir build && mkdir install git clone https://github.com/curl/curl.git…...

js函数闭包解析
闭包是JavaScript中非常重要的概念,理解闭包对于编写高质量的代码是至关重要的。本文将详细解析闭包的概念,并提供一些代码示例来帮助读者更好地理解闭包的使用。 什么是闭包? 闭包是指在一个函数内部定义的函数,该函数可以访问包…...

查看Oracle、MySQL、PostGreSQL中的依赖关系
查看Oracle、MySQL、PostGreSQL中的依赖关系 在有些程序员开发习惯中,喜欢为了应用代码的简洁或复用,而在数据库创建一个复杂关连查询的VIEW,甚至是VIEW套VIEW嵌套使用, 这里就有个问题如果上线后如发现依赖的表字段类型或长度不…...
多线程(基础)
前言👀~ 上一章我们介绍了什么是进程,对于进程就了解那么多即可,我们作为java程序员更关注线程,线程内容比较多,所以我们要分好几部分才能讲完 目录 进程的缺点 多线程(重要) 进程和线程的区…...

BUG cn.bing.com 重定向的次数过多,无法搜索内容
BUG cn.bing.com 重定向的次数过多,无法搜索内容 环境 windows 11 edge浏览器详情 使用Microsoft Edge 必应搜索显示"cn.bing.com"重定向次数过多,无法进行正常的检索功能 解决办法 检查是否开启某些科_学_上_网(翻_墙…...
)
【数据科学】学习资源汇总(不定时更新)
好书推荐:BooksPDF/数据科学/Python数据科学手册.pdf at master zhixingchou/BooksPDF GitHub...

完美解决ValueError: column index (256) not an int in range(256)的正确解决方法,亲测有效!!!
完美解决ValueError: column index (256) not an int in range(256)的正确解决方法,亲测有效!!! 亲测有效 完美解决ValueError: column index (256) not an int in range(256)的正确解决方法,亲测有效!&…...
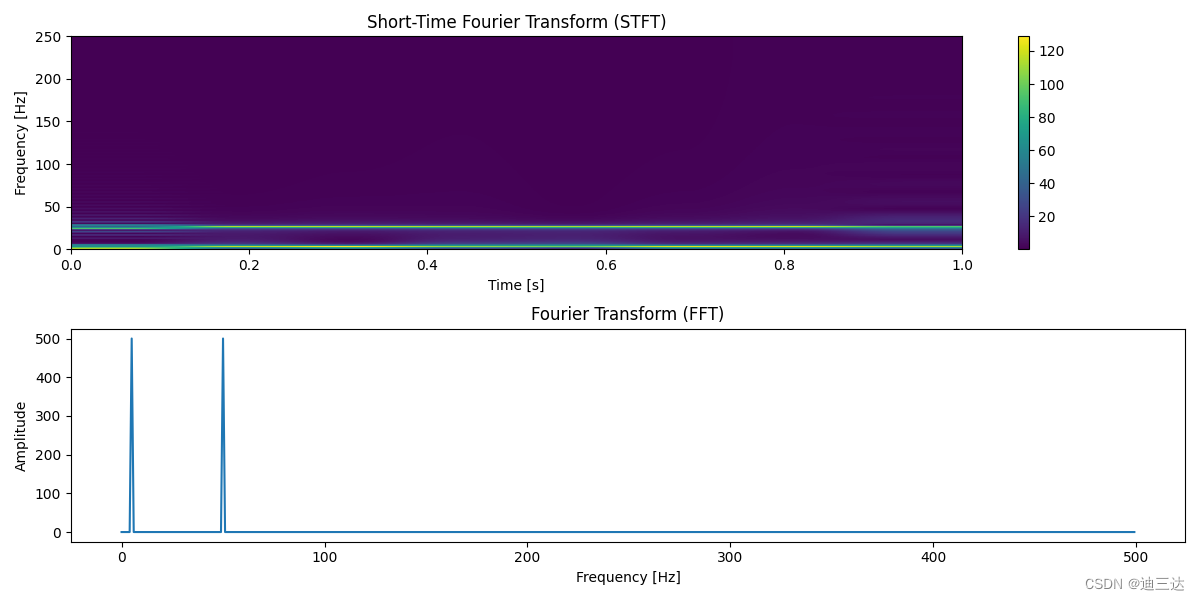
# 音频处理4_傅里叶变换
1.离散傅里叶变换 对于离散时域信号 x[n]使用离散傅里叶变换(Discrete Fourier Transform, DFT)进行频域分析。 DFT 将离散信号 x[n] 变换为其频谱表示 X[k],定义如下: X [ k ] ∑ n 0 N − 1 x [ n ] e − j 2 π k n N X[k]…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
