信息检索(57):MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS
MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS
- 摘要
- 1 引言
- 2 相关工作
- 3 预期 FLOPS 次数
- 4 我们的方法
- 5 实验
- 6 结论
发布时间(2020)
最小化 Flop 来学习高效的稀疏表示
摘要
1)学习高维稀疏表示
2)FLOP 集成到损失函数作为正则化项
3)相比 l1 损失更好
倒排索引浮点运算的数量 // 非零值的均匀分布
深度表示学习已成为视觉搜索、推荐和识别领域最广泛采用的方法之一。然而,从大型数据库中检索此类表示在计算上具有挑战性。基于学习紧凑表示的近似方法已被广泛用于解决此问题,例如局部敏感哈希、乘积量化和 PCA。在这项工作中,与学习紧凑表示相反,我们提出学习高维和稀疏表示,这些表示具有与密集嵌入相似的表示容量,同时由于稀疏矩阵乘法运算比密集乘法快得多而更高效。根据关键见解,如果非零项在维度上均匀分布,则运算次数会随着嵌入的稀疏性二次减少,我们提出了一种新方法来学习这种分布式稀疏嵌入,该方法通过使用精心构建的正则化函数直接最小化检索过程中发生的浮点运算 (FLOP) 数量的连续松弛。我们的实验表明,我们的方法与其他基线相比具有竞争力,并且在实际数据集上产生类似或更好的速度与准确度权衡。
1 引言
使用深度神经网络 (DNN) 学习语义表示现已成为视觉搜索 (Jing et al, 2015; Hadi Kiapour et al, 2015)、语义文本匹配 (Neculoiu et al, 2016)、单样本分类 (Koch et al, 2015)、聚类 (Oh Song et al, 2017) 和推荐 (Shankar et al, 2017) 等应用的一个基本方面。然而,从 DNN 生成的高维密集嵌入对于在具有数百万个实例的大规模问题中执行最近邻搜索提出了计算挑战。特别是,当嵌入维度很高时,评估任何查询与大型数据库中所有实例的距离成本很高,因此难以在不牺牲准确性的情况下进行有效搜索。与 SIFT (Lowe, 2004) 等手工制作的特征相比,使用 DNN 生成的表示通常具有更高的维度,而且是密集的。密集特征的关键警告是,与词袋特征不同,它们无法通过倒排索引进行有效搜索,也无法进行近似。
由于在实践中,高维度上的精确搜索成本过高(Wang,2011),因此人们通常不得不牺牲准确性来换取效率,而采用近似方法。因此,解决高效近似最近邻搜索 (NNS)(Jegou 等人,2011)或最大内积搜索 (MIPS)(Shrivastava 和 Li,2014)的问题是一个活跃的研究领域,我们将在相关工作部分简要回顾一下。大多数方法(Charikar,2002;Jegou 等人,2011)旨在学习保留距离信息的紧凑低维表示。
虽然在学习紧凑表示方面已经有大量研究,但学习稀疏的高维表示直到最近才开始得到解决(Jeong 和 Song,2018;Cao 等人,2018)。作为一个开创性的例子,Jeong 和 Song(2018)提出了一种端到端方法来学习稀疏和高维哈希,与密集嵌入相比,在基准数据集上的检索时间显著加快。这种方法也从生物学的角度(Li 等人,2018)出发,与果蝇的嗅觉回路有关,从而表明使用更高维度进行哈希的可能性,而不是降低维度
同样,在这项工作中,我们建议学习稀疏的高维嵌入,因此使用稀疏矩阵乘法运算可以有效地检索。与通常会导致表示能力下降的紧凑低维 ANN 式表示相比,我们的高维稀疏嵌入的一个关键方面是它们可以具有与初始密集嵌入相同的表示容量。我们方法背后的核心思想受到两个关键观察的启发:(i)检索平均非零值比例为 p 的 d(高)维稀疏嵌入可以加快 1=p 倍。(ii)通过确保非零值均匀分布在所有维度上,可以将速度进一步提高到 1=p2 倍。 这表明,仅靠稀疏性不足以确保最大加速;非零值的分布也起着重要作用。这促使我们考虑稀疏性对使用倒排索引进行检索所需的浮点运算 (FLOP) 数量的影响。 我们提出了一个嵌入向量惩罚函数,它是 FLOP 的精确数量的连续放松,并鼓励非零值在各个维度上均匀分布。
我们将我们的方法应用于学习面部图像嵌入的大规模度量学习问题。我们的训练损失包括度量学习(Weinberger 和 Saul,2009)损失,旨在学习模仿所需度量的嵌入,以及 FLOPs 损失以最小化操作次数。我们在 Megaface 数据集(Kemelmacher-Shlizerman 等人,2016)上对我们的方法进行了实证评估,并表明我们提出的方法成功地学习了高维稀疏嵌入,速度提高了几个数量级。我们将我们的方法与多个基线进行了比较,证明了速度与准确度之间的权衡有所改善或相似。
本文的其余部分组织如下。在第 3 节中,我们分析了预期的 FLOP 数量,并推导出了其精确表达式。在第 4 节中,我们推导出可用作正则化器的连续松弛,并使用梯度下降进行优化。我们还为我们的松弛提供了一些分析依据。然后,在第 5 节中,我们在一个大型度量学习任务上比较了我们的方法,结果显示与基线相比,速度-准确度权衡有所改善。
2 相关工作
学习紧凑表示,ANN
对于从深度神经网络中学习到的高维密集嵌入,精确检索前 k 个最近邻居在实践中成本很高,从业者通常求助于近似最近邻居 (ANN) 来实现高效检索。 ANN 的流行方法包括依赖于随机投影的局部敏感哈希 (LSH) (Gionis 等,1999;Andoni 等,2015;Raginsky 和 Lazebnik,2009)、基于通过在数据中查找聚类来构建有效搜索图的可导航小世界图 (NSW) (Malkov 等,2014) 和分层 NSW (HNSW) (Malkov 和 Yashunin,2018)、将原始空间分解为低维子空间的笛卡尔积并分别量化每个子空间的乘积量化 (PQ) (Ge 等,2013;Jegou 等,2011) 方法,以及谱哈希 (Weiss 等,2009),它涉及计算最佳二进制哈希的 NP 难题,该问题被放宽为连续值哈希,相似矩阵的谱。总体而言,为了紧凑表示并加快查询时间,这些方法中的大多数使用各种精心选择的数据结构,例如哈希(Neyshabur 和 Srebro,2015;Wang 等人,2018)、局部敏感哈希(Andoni 等人,2015)、倒排文件结构(Jegou 等人,2011;Baranchuk 等人,2018)、树(Ram 和 Gray,2012)、聚类(Auvolat 等人,2015)、量化草图(Jegou 等人,2011;Ning 等人,2016),以及基于主成分分析和 t-SNE 的降维(Maaten 和 Hinton,2008)。
端到端ANN
端到端学习 ANN 结构是最近越来越流行的另一项工作。Norouzi 等人(2012 年)提出通过最小化基于边距的三重态损失来学习汉明度量的二进制表示。Erin Liong 等人(2015 年)使用深度神经网络的有符号输出作为哈希,同时对哈希位施加独立性和正交性条件。其他用于学习哈希的端到端学习方法包括(Cao 等人,2016 年;Li 等人,2017 年)。端到端方法的一个优点是它们学习与特征表示最佳兼容的哈希码。
学习稀疏表示
稀疏深度哈希 (SDH) (Jeong and Song,2018) 是一种端到端方法,它涉及从预先训练的网络开始,然后执行由两个最小化步骤组成的交替最小化,一个用于训练二进制哈希,另一个用于训练连续密集嵌入。第一步涉及使用最小成本最大流方法计算与密集嵌入最兼容的最佳哈希。第二步是梯度下降步骤,通过最小化度量学习损失来学习密集嵌入。高维稀疏嵌入的思想也得到了稀疏提升方法 (Li et al,2018) 的强化,其中稀疏高维嵌入是从密集特征中学习的。这个想法受到受生物启发的苍蝇算法 (Dasgupta et al,2017) 的启发。实验结果表明,与依赖降维的 LSH 等传统技术相比,稀疏提升在精度和速度方面都有所提高。
l1 正则化,Lasso
Lasso(Tibshirani,1996)是施加稀疏性的最流行方法,已用于各种应用,包括稀疏化和压缩神经网络(Liu et al,2015;Wen et al,2016)。组套索(Meier et al,2008)是套索的扩展,它鼓励同时选择指定组中的所有特征。另一方面,另一种扩展,排他套索(Kong et al,2014;Zhou et al,2010),旨在选择组中的单个特征。我们提出的正则化器最初是受最小化 FLOP 的想法的启发,与排他套索非常相似。然而,我们的重点是稀疏生成的嵌入,而不是稀疏参数。
度量学习
虽然学习嵌入存在许多设置(Hinton 和 Salakhutdinov,2006 年;Kingma 和 Welling,2013 年;Kiela 和 Bottou,2014 年),但在本文中,我们将注意力限制在度量学习的背景下(Weinberger 和 Saul,2009 年)。度量学习损失的一些示例包括 CNN 的大边距 softmax 损失(Liu 等人,2016 年)、三重态损失(Schroff 等人,2015 年)和基于代理的度量损失(Movshovitz-Attias 等人,2017 年)。
3 预期 FLOPS 次数
在本节中,我们研究稀疏性对检索所需的预期 FLOP 数量的影响,并推导出预期 FLOP 数量的精确表达式。本文的主要思想基于以下关键见解:如果嵌入的每个维度都以概率 p(不一定独立)非零,则可以使用嵌入集上的倒排索引将速度提高到 1=p2 的量级。考虑两个嵌入向量 u;v。 计算 u T v 只需要计算索引 k 处的逐点积,其中 uk 和 vk 都非零。这是使用倒排索引的主要动机,并导致上述加速。在更正式地分析它之前,我们先介绍一些符号。
令 D = f(xi ; yi)g n i=1 为根据分布 P 从 Z = X × Y 中抽取的 n 个独立训练样本集合,其中 X ; Y 分别表示输入空间和标签空间。令 F = ffθ : X ! R d j θ 2 Θg 为一类由 θ 2 Θ 参数化的函数,将输入实例映射到 d 维嵌入。通常,对于图像任务,选择合适的 CNN 作为函数(Krizhevsky et al, 2012)。假设 X; Y ∼ P,则定义激活概率 pj = P(fθ(X)j 6= 0),及其经验版本 p¯j = 1 n Pn i=1 I[fθ(xi)j 6= 0]。
我们现在证明稀疏嵌入可以带来二次加速。考虑一个 d 维稀疏查询向量 uq = fθ(xq) 2 R d 和一个由 n 个稀疏向量组成的数据库 fvi = fθ(x (i) )g n i=1 ⊂ R d ,它们形成一个矩阵 D 2 R n×d 。我们假设 xq;x (i) (i = 1; : : : ; n) 独立于 P 采样。计算向量矩阵乘积 Duq 只需要查看 D 中与 uq 的非零项相对应的列,由 Nq = fj j j 2 [1 : d];(uq)j 6= 0g 给出。 1 此外,在每一列中,我们只需要查看非零项。这可以在实践中通过将每列的非零索引存储在独立列表中来有效实现,如图 1a 所示。
产生的 FLOP 数量由下式给出:
请注意,对于固定的稀疏度 Pd j=1 pj = d p,当每个维度都以相等的概率 pj = p; 8j 2 [1 : d] 非零时,稀疏度会最小化,此时 F(fθ;P) = d p2(因此,作为正则化器,F(fθ;P) 反过来会鼓励跨维度的这种均匀分布)。给定这种均匀分布,与每行复杂度为 O(d) 的密集乘法相比,我们得到的改进是 1=p2 (p < 1)。因此,当所有条目中只有 p 部分非零,并均匀分布在所有列上时,我们实现了 1=p2 的加速。请注意,由于期望的线性,非零索引的独立性不是必需的。
4 我们的方法
l1 正则化是最常见的引入稀疏性的方法。但是,正如我们将通过实验验证的那样,它不能确保非零值在所有维度上均匀分布,而这是实现最佳加速所需的。因此,我们诉诸于将实际产生的 FLOP 直接纳入损失函数,这将导致搜索时间和准确度之间的最佳权衡。FLOP F(;P) 是模型参数的不连续函数,很难优化,因此我们将改用连续松弛法进行优化。
5 实验
6 结论
在本文中,我们提出了一种学习高维嵌入的新方法,目的是提高检索任务的效率。我们的方法将检索过程中产生的 FLOP 集成到损失函数中作为正则化器,并通过连续松弛直接对其进行优化。我们通过展示所提出的方法有利于非零激活在所有维度上的均匀分布,进一步深入了解了我们的方法。我们通过实验表明,与‘1 正则化器相比,我们的方法确实可以实现更均匀的分布。我们将我们的方法与许多其他基线进行了比较,并表明它具有更好的速度与准确度权衡。总的来说,我们能够证明稀疏嵌入比密集嵌入快 50 倍左右,而不会显着降低准确度。
相关文章:
:MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS)
信息检索(57):MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS
MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS 摘要1 引言2 相关工作3 预期 FLOPS 次数4 我们的方法5 实验6 结论 发布时间(2020) 最小化 Flop 来学习高效的稀疏表示 摘要 1)学习高维稀疏表示 2)FLOP 集成到损失…...

Python 面试【中级】
欢迎莅临我的博客 💝💝💝,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...
[Open-source tool]Uptime-kuma的簡介和安裝於Ubuntu 22.04系統
[Uptime Kuma]How to Monitor Mqtt Broker and Send Status to Line Notify Uptime-kuma 是一個基於Node.js的開軟軟體,同時也是一套應用於網路監控的開源軟體,其利用瀏覽器呈現直觀的使用者介面,如圖一所示,其讓使用者可監控各種…...

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 灰度图像恢复(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

leetcode494. 目标和
1.思想方法 2.代码 class Solution { public int findTargetSumWays(int[] nums, int target) {int sum 0;for(int num : nums)sum num;if(sum < Math.abs(target) || (targetsum)%2 ! 0)return 0;int x (targetsum) / 2,n nums.length;//基于滚动数组的方法int[] dp…...

数据结构简介
在容器的基础之上,java引入了数据结构的概念。数据结构可以简单地理解成是一个以特定的布局方式来存储数据的容器。但是我个人觉得这种理解方式不太合理,根据我们学的数据结构的内容,我更倾向于数据结构是数据在容器中的布局方式,…...
PyScript:在浏览器中释放Python的强大
PyScript:Python代码,直接在网页上运行。- 精选真开源,释放新价值。 概览 PyScript是一个创新的框架,它打破了传统编程环境的界限,允许开发者直接在浏览器中使用Python语言来创建丰富的网络应用。结合了HTML界面、Pyo…...

巴黎成为欧洲AI中心 大学开始输出AI创始人
来自Dealroom 的数据显示,在欧洲和以色列AI创业公司中,法国的AI创业公司资金最充裕。Mistral、Owkin、Hugging Face等法国企业已经融资23亿美元,比英国、德国AI创业公司都要多。 一名大学生走出校门凭借聪明才智和一个黄金点子成为富豪&#…...
完全离线的本地问答模型LocalGPT如何实现无公网IP远程连接提问
文章目录 前言环境准备1. localGPT部署2. 启动和使用3. 安装cpolar 内网穿透4. 创建公网地址5. 公网地址访问6. 固定公网地址 前言 本文主要介绍如何本地部署LocalGPT并实现远程访问,由于localGPT只能通过本地局域网IP地址端口号的形式访问,实现远程访问…...

【算法专题--栈】栈的压入、弹出序列 -- 高频面试题(图文详解,小白一看就懂!!)
目录 一、前言 二、题目描述 三、解题方法 💧栈模拟法💧-- 双指针 ⭐ 解题思路 ⭐ 案例图解 四、总结与提炼 五、共勉 一、前言 栈的压入、弹出序列 这道题,可以说是--栈专题--,最经典的一道题,也是在…...

如何高效安全的开展HPC数据传输,保护数据安全?
高性能计算(HPC)在多个行业和领域中都有广泛的应用,像科学研究机构、芯片IC设计企业、金融、生物制药、能源、航天航空等。HPC(高性能计算)环境中的数据传输是一个关键环节,它涉及到将数据快速、安全地在不…...

Java部分复习笔记整理
一、Java常用类 1.String类 表示字符串,不可变,常用方法包括length(), charAt(), substring(), indexOf(), equals()等。 2.ArrayList类 基于数组实现的动态数组,可变大小,常用方法包括add(), get(), set(), remove(), size()…...

GoLang语言
基础 安装Go扩展 go build 在项目目录下执行go build go run 像执行脚本文件一样执行Go代码 go install go install分为两步: 1、 先编译得到一个可执行文件 2、将可执行文件拷贝到GOPATH/bin Go 命令 go build :编译Go程序 go build -o "xx.exe"…...

ctfshow web入门 sqli-labs web517--web524
web517 注入点id ?id-1’union select 1,2,3– 确认是否能够注入 ?id-1union select 1,database(),3-- 爆出库名 security爆出表名 ?id-1union select 1,(select group_concat(table_name) from information_schema.tables where table_schemasecurity),3-- emails,refer…...

Spring Cloud Gateway 跨域配置和跨服务请求跟踪
文章目录 引言I Spring Cloud Gateway 跨域配置1.1 网关统一处理:配置文件-推荐1.2 网关统一处理:配置类方式1.3 微服务处理,网关侧不用处理CORS。1.4 子服务依赖配置1.5 网关服务的依赖配置II 跨服务请求日志跟踪2.1 feign 依赖配置2.2 feign子模块将请求头中的参数,全部作…...

动手学深度学习(Pytorch版)代码实践 -卷积神经网络-29残差网络ResNet
29残差网络ResNet import torch from torch import nn from torch.nn import functional as F import liliPytorch as lp import matplotlib.pyplot as plt# 定义一个继承自nn.Module的残差块类 class Residual(nn.Module):def __init__(self, input_channels, num_chan…...
解锁音乐潮流:使用TikTok API获取平台音乐信息
一、引言 TikTok,作为全球领先的短视频社交平台,不仅为用户提供了展示自我、分享生活的舞台,还为用户带来了丰富多样的音乐体验。在TikTok上,音乐与视频内容的结合,为用户带来了全新的视听盛宴。对于音乐制作人、品牌…...

基于yolo的物体识别坐标转换
一、模型简介: 1.1、小孔成像模型简图如下:不考虑实际相机中存在的场曲、畸变等问题 相对关系为: 为了表述与研究的方便,我们将像面至于小孔之前,且到小孔的距离仍然是焦距f,这样的模型与原来的小孔模型是等价的 相对关系为: 二、坐标系简介: **世界坐标系(world coo…...
STM32第七课:KQM6600空气质量传感器
文章目录 需求一、KQM6600模块及接线方法二、模块配置流程1.环境2.配置时钟和IO3.配置串口初始化,使能以及中断4.中断函数 三、数据处理四、关键代码总结 需求 能够在串口实时显示当前的VOC(挥发性有机化合物),甲醛和Co2浓度。 …...
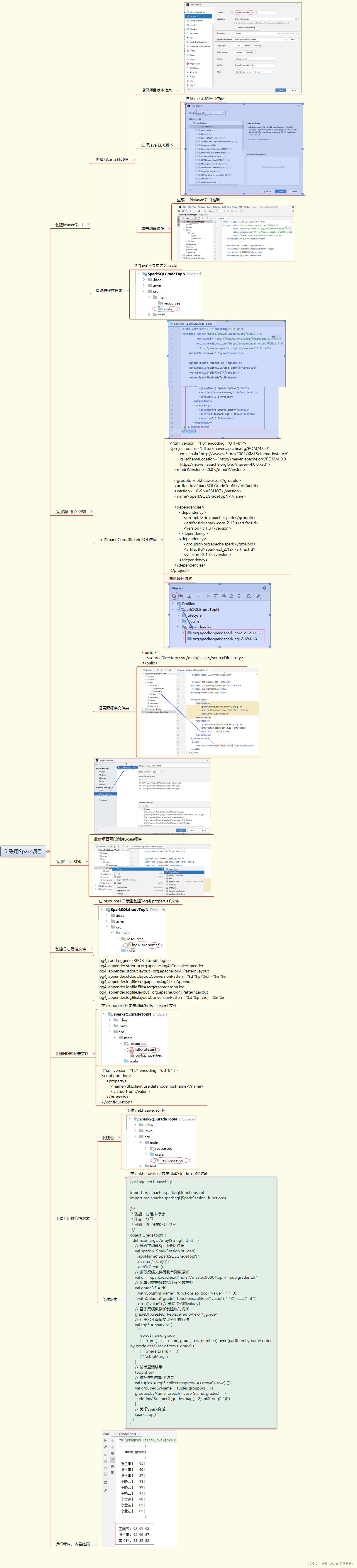
任务4.8.4 利用Spark SQL实现分组排行榜
文章目录 1. 任务说明2. 解决思路3. 准备成绩文件4. 采用交互式实现5. 采用Spark项目实战概述:使用Spark SQL实现分组排行榜任务背景任务目标技术选型实现步骤1. 准备数据2. 数据上传至HDFS3. 启动Spark Shell或创建Spark项目4. 读取数据5. 数据转换6. 创建临时视图…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
