[C++][数据结构][图][中][图的遍历][最小生成树]详细讲解
目录
- 1.图的遍历
- 1.广度优先遍历
- 2.深度优先遍历
- 2.最小生成树
- 1.Kruskal算法
- 2.Prim算法
1.图的遍历
- 给定一个图G和其中任意一个顶点 v 0 v_0 v0,从 v 0 v_0 v0出发,沿着图中各边访问图中的所有顶点,且每个顶 点仅被遍历一次
- “遍历”:对结点进行某种操作的意思
1.广度优先遍历
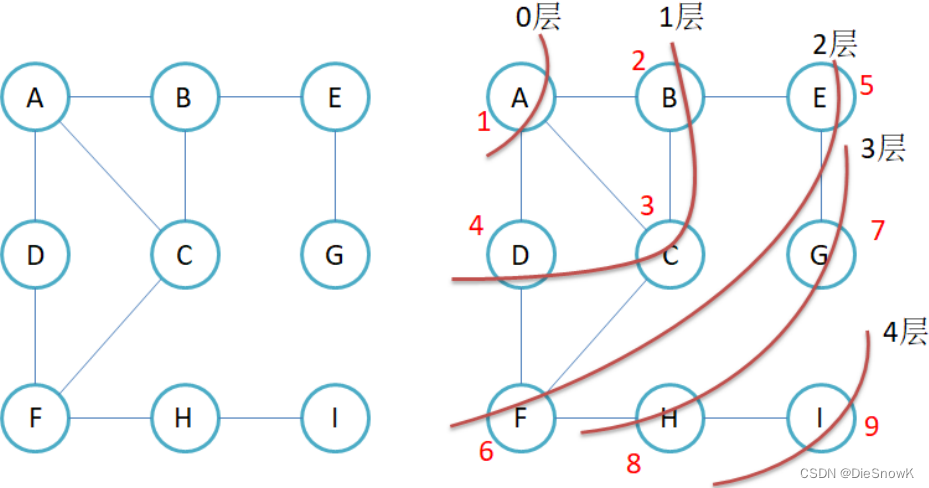
-
**例如:**现在要找东西,假设有三个抽屉,东西在哪个抽屉不清楚,现在要将其找到,广度优先遍历的做法是:
- 先将三个抽屉打开,在最外层找一遍
- 将每个抽屉中红色的盒子打开,再找一遍
- 将红色盒子中绿色盒子打开,再找一遍
- 直到找完所有的盒子
- 注意:每个盒子只能找一次,不能重复找
- 注意:每个盒子只能找一次,不能重复找
-
思考:如何防止节点被重复遍历?
- 增加一个数组,用于标记是否入过队列,这样可以防止重复遍历
void BFS(const V& src)
{size_t srci = GetVertexIndex(src);queue<int> q;vector<bool> visited(_vertexs.size(), false); // 标记数组q.push(srci);visited[srci] = true;int levelSize = 1; // 控制每层出的数量while (!q.empty()){// 一层一层出for (size_t i = 0; i < levelSize; i++){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";// 把front的邻接顶点入队列for (size_t j = 0; j < _vertexs.size(); j++){if (_matrix[front][j] != MAX_W && visited[j] == false){q.push(j);visited[j] = true;}}}cout << endl;levelSize = q.size();}
}
2.深度优先遍历
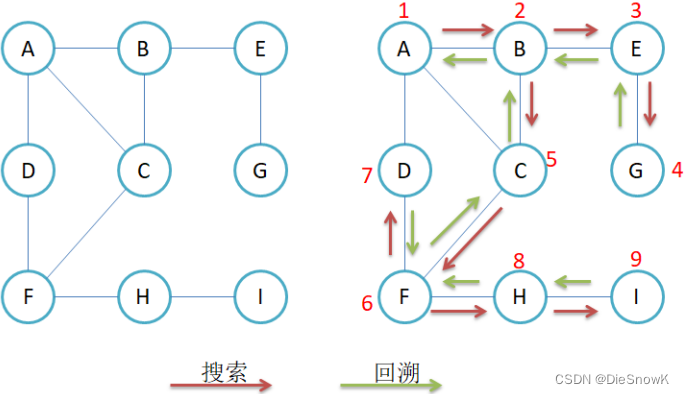
- **例如:**现在要找东西,假设有三个抽屉,东西在哪个抽屉不清楚,现在要将其找到,深度优先遍历的做法是:
- 先将第一个抽屉打开,在最外层找一遍
- 将第一个抽屉中红盒子打开,在红盒子中找一遍
- 将红盒子中绿盒子打开,在绿盒子中找一遍
- 递归查找剩余的两个盒子
- **深度优先遍历:**将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子),再去递归遍历其他盒子
- 如果给的图不是连通图,以某个顶点为起点没有遍历完成,怎么保证遍历完剩下的顶点?
- 在visited数组中找没有遍历过的顶点,再次进行遍历
void _DFS(size_t srci, vector<bool>& visited)
{cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (size_t i = 0; i < _vertexs.size(); i++){if (_matrix[i] != MAX_W && visited[i] == false){_DFS(i, visited);}}
}void DFS(const V& src)
{size_t srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);// 处理存在不连通的情况for (size_t i = 0; i < _vertexs.size(); i++){if (!visited[i]){_DFS(i, visited);}}
}
2.最小生成树
- 连通图中的每一棵生成树,都是原图的一个极大无环子图,即:
- 从其中删去任何一条边,生成树就不在连通
- 反之,在其中引入任何一条新边,都会形成一条回路
- 若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边,因此构造最小生成树的准则有三条:
- 只能使用图中权值最小的边来构造最小生成树
- 最小的成本让着N个顶点连通
- 只能使用恰好n-1条边来连接图中的n个顶点
- 选用的n-1条边不能构成回路
- 只能使用图中权值最小的边来构造最小生成树
- 构造最小生成树的方法:Kruskal算法和Prim算法,这两个算法都采用了逐步求解的贪心策略
- 贪心算法:
- 指在问题求解时,总是做出当前看起来最好的选择
- 即:贪心算法做出的不是整体最优的的选择,而是某种意义上的局部最优解
- 贪心算法不是对所有的问题都能得到整体最优解
- 指在问题求解时,总是做出当前看起来最好的选择
1.Kruskal算法
- 任给一个有n个顶点的连通网络 N = { V , E } N=\{V,E\} N={V,E}
- 首先构造一个由这n个顶点组成、不含任何边的图 G = { V , N U L L } G=\{V,NULL\} G={V,NULL},其中每个顶点自成一个连通分量
- 其次不断从E中取出权值最小的一条边(若有多条任取其一),若该边的两个顶点来自不同的连通分量,则将此边加入到G中
- 如此重复,直到所有顶点在同一个连通分量上为止
- 核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树
- Kruskal算法是一种全局贪心的算法
- 如何判断是否形成环?
- 并查集
- 在下图执行Kruskal算法的过程
- 加了阴影的边属于不断增长的森林A
- 该算法按照边的权重大小依次进行考虑,箭头指向的边是算法每一步考察的边
- 如果该条边将两颗不同的树连接起来,它就被加入到森林里,从而完成对两棵树的合并
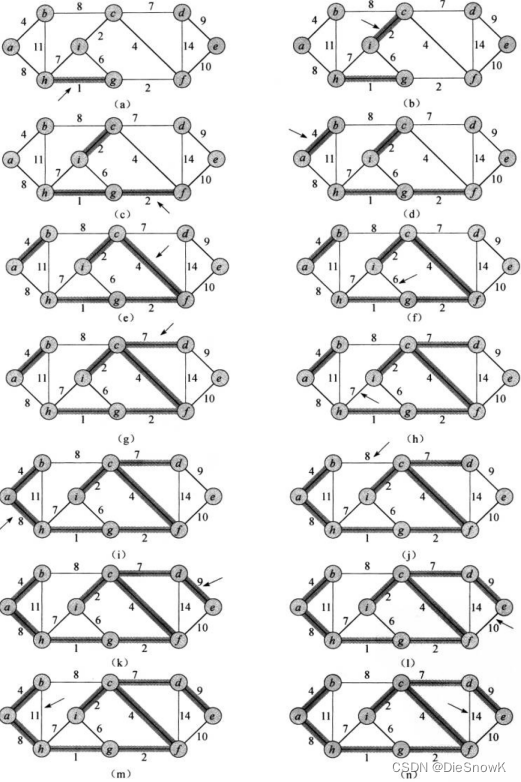
- 如果该条边将两颗不同的树连接起来,它就被加入到森林里,从而完成对两棵树的合并
W Kruskal(Self& minTree)
{size_t n = _vertexs.size();// 初始化minTreeminTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; i++){minTree._matrix[i].resize(n, MAX_W);}priority_queue<Edge, vector<Edge>, greater<Edge>> minQueue;// 建堆排序for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (i < j && _matrix[i][j] != MAX_W){minQueue.push(Edge(i, j, _matrix[i][j]));}}}// 选出n-1条边size_t size = 0;W totalW = W();UnionFindSet ufs(n);while (!minQueue.empty()){Edge min = minQueue.top();minQueue.pop();// 判环 -> 并查集if (!ufs.InSameSet(min._srci, min._dsti)){cout << _vertexs[min._srci] << "->" \<< _vertexs[min._dsti] << ":" << min._w << endl;minTree._AddEdge(min._srci, min._dsti, min._w);ufs.Union(min._srci, min._dsti); // 入集size++;totalW += min._w;}else{cout << "Forming Ring: ";cout << _vertexs[min._srci] << "->" \<< _vertexs[min._dsti] << ":" << min._w << endl;}}if (size == n - 1){return totalW;}else{return W();}
}
2.Prim算法
- Prim算法的一个性质是集合A中的边总是构成一棵树,这棵树从一个任意的根节点r开始,一直长大到覆盖V中的所有结点时为止
- Prim算法思路天然避环
- 算法每一步在连续集合A和A之外的结点的所有边中,选择一条轻量级边加入到A中
- 本策略也属于贪心策略,因为每一步所加入的边都必须是使树的总权重增加量最小的边
- Prim算法是一种局部贪心算法
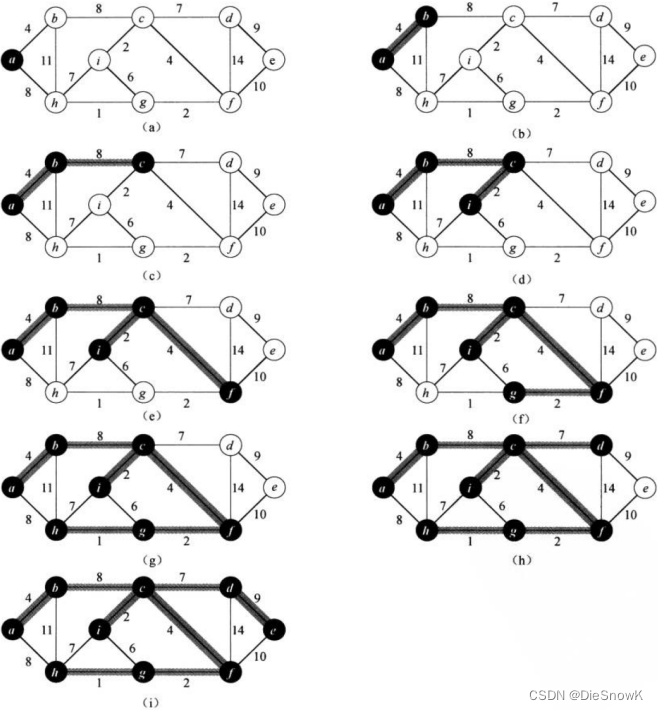
- 在下图执行Prim算法的过程
- 初始的根节点为a,加阴影的边和黑色的结点都属于树A
- 在算法的每一步,树中的结点就决定了图的一个切割,横跨该切割的一条轻量级边被加入到树中
- **例如:**在途中第二步,该算法可以选择将边 ( b , c ) (b, c) (b,c)加入到树中,也可以将边 ( a , h ) (a, h) (a,h)加入到树中,因为这两条边都是横跨该切割的轻量级边
W Prim(Self& minTree, const W& src)
{size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();// 初始化minTreeminTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; i++){minTree._matrix[i].resize(n, MAX_W);}// true & false表示该元素是否在该集合内vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;// 从X->Y集合中连接的边里面选出最小的边priority_queue<Edge, vector<Edge>, greater<Edge>> minQueue;// 先把srci连接的边添加到队列中for (size_t i = 0; i < n; i++){if (_matrix[srci][i] != MAX_W){minQueue.push(Edge(srci, i, _matrix[srci][i]));}}size_t size = 0;W totalW = W();while (!minQueue.empty()){Edge min = minQueue.top();minQueue.pop();// 最小边的目标也在X集合,则构成环if (X[min._dsti]){cout << "Forming Ring:";cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}else{cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;minTree._AddEdge(min._srci, min._dsti, min._w);X[min._dsti] = true;Y[min._dsti] = false;size++;totalW += min._w;// 可能最小生成树已经生成,但是多了很多成环边,无须继续遍历if (size == n - 1){break;}// 将目标顶点连接的边加入到队列中for (size_t i = 0; i < n; i++){if (_matrix[min._dsti][i] != MAX_W && Y[i]){minQueue.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}// 实际不一定存在最小生成树if (size == n - 1){return totalW;}else{return W();}
}
相关文章:

[C++][数据结构][图][中][图的遍历][最小生成树]详细讲解
目录 1.图的遍历1.广度优先遍历2.深度优先遍历 2.最小生成树1.Kruskal算法2.Prim算法 1.图的遍历 给定一个图G和其中任意一个顶点 v 0 v_0 v0,从 v 0 v_0 v0出发,沿着图中各边访问图中的所有顶点,且每个顶 点仅被遍历一次 “遍历”&…...

退市新规解读—财务类强制退市
一、退市风险警示:第一年触及相关指标 上市公司最近一个会计年度触及下列退市风险指标之一,公司股票或存托凭证被实施退市风险警示(*ST): 第1项 组合类财务指标 仅发行A股或B股,最近一个会计年度或追溯重述后最近一个会计年度 …...

小程序的生命周期使用方法和应用场景
小程序生命周期 初始化(App Launch) • 触发时机:小程序首次启动时。 • 主要事件:onLaunch。 • 功能与适用场景: • 全局数据初始化:设置应用的全局状态和变量。 • 登录状态检查:判断用户是…...

什么是C++模块化系统?C++20的模块化系统。
C20引入的模块化系统是一种新的代码组织和编译机制,它旨在替代传统的头文件机制,提供更好的代码组织、更快的编译速度和更强的封装性。模块化系统的主要目标包括: 减少编译时间:通过减少冗余的头文件解析和宏定义传播,…...

智慧校园-档案管理系统总体概述
智慧校园档案管理系统,作为教育信息化进程中的重要一环,它运用现代信息技术的力量,彻底改变了传统档案管理的面貌,为学校档案资源的收集、整理、存储、检索与利用开辟了全新的途径。这一系统全面覆盖学生、教职工、教学科研及行政…...
文心一言 VS 讯飞星火 VS chatgpt (290)-- 算法导论21.3 3题
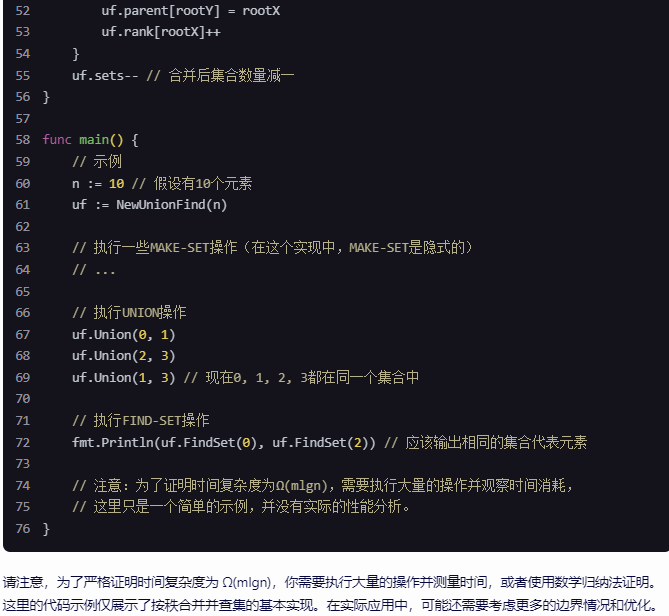
三、给出一个包含 m 个 MAKE-SET 、UNION 和 FINDSET 操作的序列(其中有 n 个是 MAKE-SET 操作),当仅使用按秩合并时,需要 Ω(mlgn) 的时间。如果要写代码,请用go语言。 文心一言: 在并查集(Union-Find)数…...

逻辑回归梯度推导
逻辑回归是一种广泛使用的分类算法,用于估计一个事件发生的概率。它是线性回归的扩展,通过sigmoid函数将线性回归的输出映射到[0, 1]区间,从而用于分类任务。 在逻辑回归中,我们使用对数似然损失函数(log-likelihood l…...

Python 使用函数输出一个整数的逆序数
在Python中,你可以定义一个函数来输出一个整数的逆序数。这里有一个简单的实现方法: def reverse_integer(x):# 检查输入是否为整数if not isinstance(x, int):raise ValueError("Input must be an integer")# 将整数转换为字符串,…...
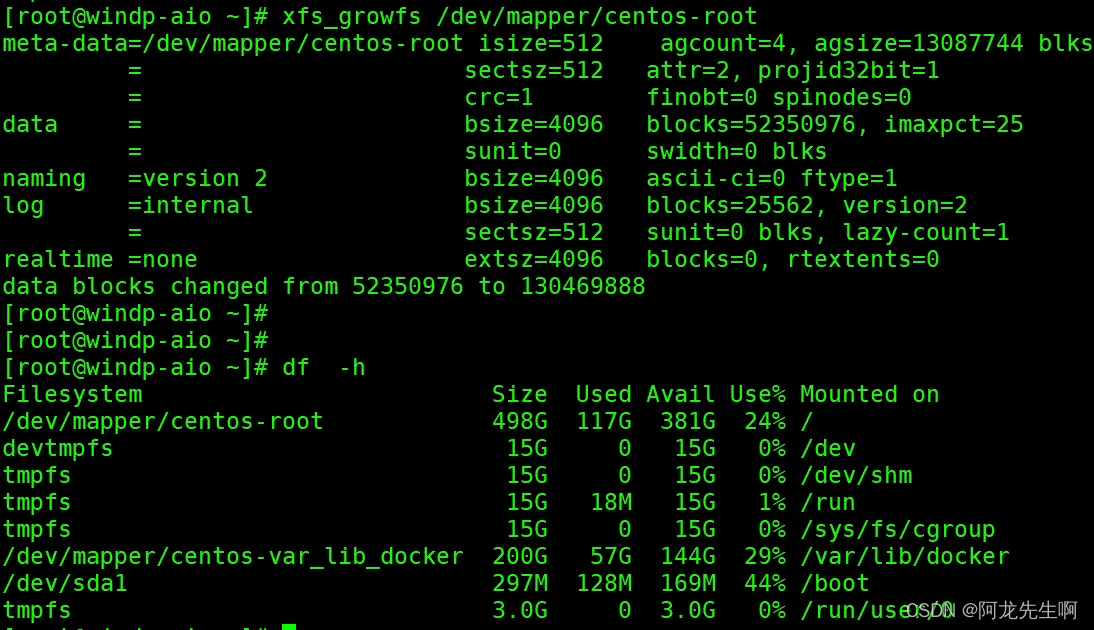
【Linux】Wmware Esxi磁盘扩容
目录 一、概述 1.1 磁盘分区概念 1.2 LVM概念 二、扩容步骤 二、报错 一、概述 1.1 磁盘分区概念 在 Linux 中,每一个硬件设备都映射到一个系统的文件,对于硬盘、光驱等 IDE 或 SCSI 设备也不例外。Linux把各种 IDE 设备分配了一个由 hd 前缀组成的文…...
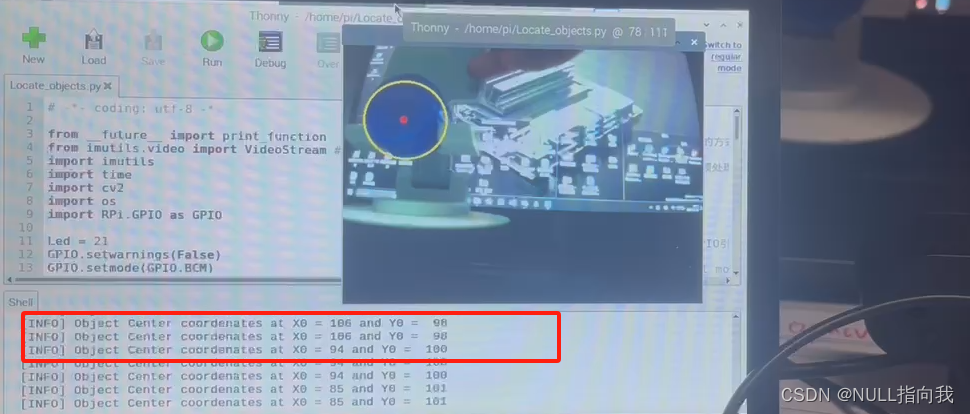
树莓派4B_OpenCv学习笔记15:OpenCv定位物体实时坐标
今日继续学习树莓派4B 4G:(Raspberry Pi,简称RPi或RasPi) 本人所用树莓派4B 装载的系统与版本如下: 版本可用命令 (lsb_release -a) 查询: Opencv 版本是4.5.1: 今日学习 OpenCv定位物体实时位置,代码来源是…...

MySQL之如何定位慢查询
1、如何定位慢查询 1.1、使用开源工具 调试工具:Arthas 运维工具:Promethuss、Skywalking 1.2、MySQL自带慢日志 慢查询日志记录了所有执行时间超过指定参数(long_query_time,单位:秒,默认10秒&#x…...

Open3D 删除点云中重复的点
目录 一、算法原理1、重叠点2、主要函数二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 1、重叠点 原始点云克隆一份 构造重叠区域 合并点云获得重叠点 2、主要…...

填报志愿选专业是兴趣重要还是前景重要?
进行专业评估,找到一个适合自己的专业是一件非常困难的事情。在进行专业选择时,身上理想化色彩非常严重的人,会全然不顾及他人的劝阻,义无反顾的以兴趣为主,选择自己热爱的专业。一些较多考虑他人建议,能听…...

python开发基础——day9 函数基础与函数参数
一、初识函数(function) 编程函数!数学函数,里面的是逻辑,功能,而不是套公式 编程函数的作用实现特定操作的一段代码 你现在请客,每个人都点同样的一份吃的,请100个人 1.薯条 2.上校鸡块 3.可乐 那…...
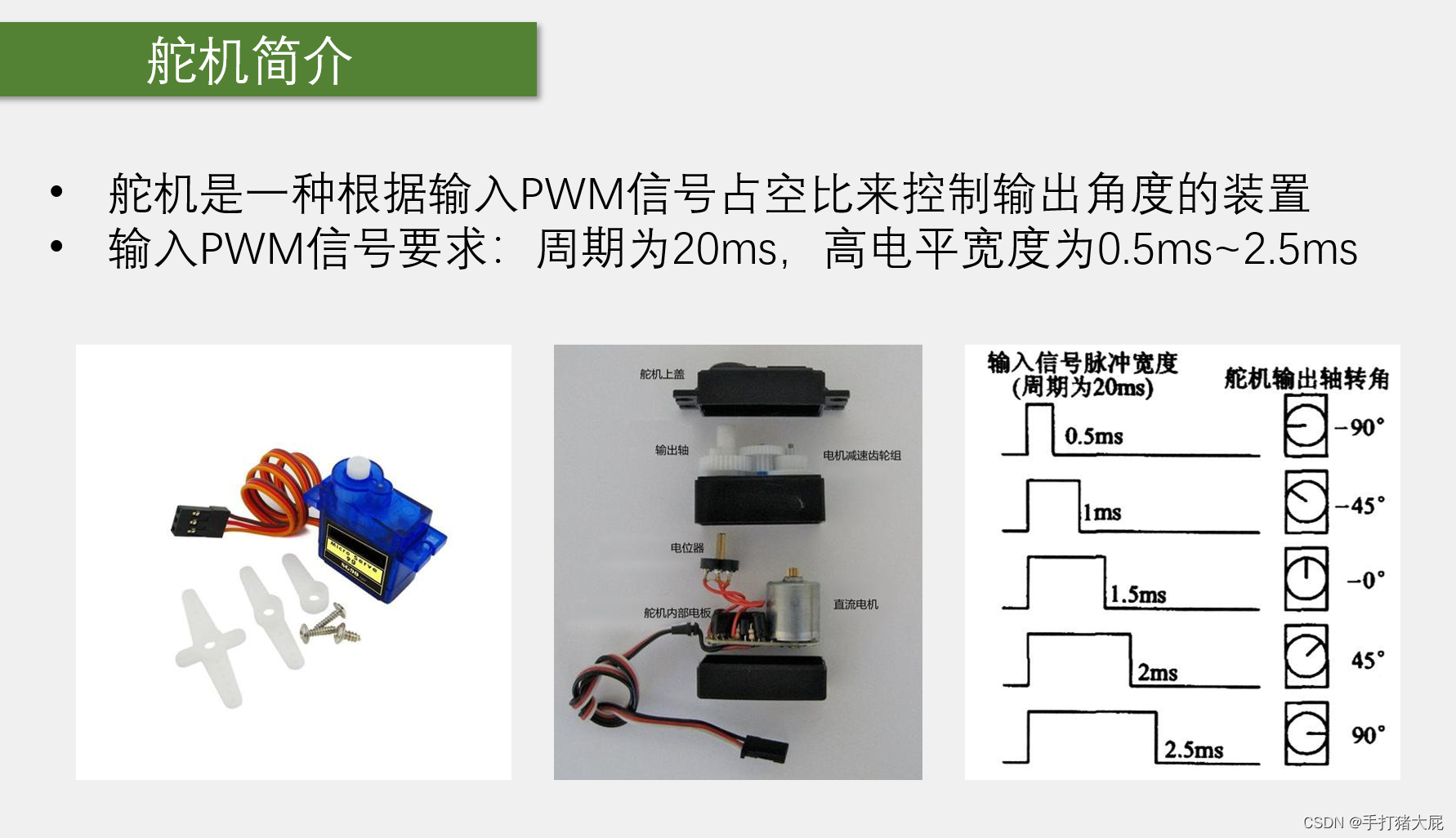
STM32——使用TIM输出比较产生PWM波形控制舵机转角
一、输出比较简介: 只有高级定时器和通用寄存器才有输入捕获/输出比较电路,他们有四个CCR(捕获/比较寄存器),共用一个CNT(计数器),而输出比较功能是用来输出PWM波形的。 红圈部分…...
(Python))
第十五章 集合(set)(Python)
文章目录 前言一、集合 前言 集合(set)是一个无序的不重复元素序列。 一、集合 set {1, 2, 3, 4}...

面试-javaIO机制
1.BIO BIO:是传统的javaIO以及部分java.net下部分接口和类。例如,socket,http等,因为网络通信同样是IO行为。传统IO基于字节流和字符流进行操作。提供了我们最熟悉的IO功能,譬如基于字节流的InputStream 和OutputStream.基于字符流…...

在.NET Core中,config和ConfigureServices的区别和作用
在.NET Core中,config和ConfigureServices是两个不同的概念,它们在应用程序的启动和配置过程中扮演着不同的角色。 ConfigureServices:这是ASP.NET Core应用程序中的一个方法,位于Startup类的内部。它的作用是配置依赖注入(DI)容器…...

App Inventor 2 如何实现多个定时功能?
1、可以使用多个“计时器”组件。 2、也可以用一个计时器,定时一分钟。也就是一分钟就会触发一次事件执行,定义一个全局数字变量,在事件中递增,用逻辑判断这个变量的值即可完成多个想要定时的任务(о∀о) 代码块请参考…...

技术驱动的音乐变革:AI带来的产业重塑
📑引言 近一个月来,随着几款音乐大模型的轮番上线,AI在音乐产业的角色迅速扩大。这些模型不仅将音乐创作的门槛降至前所未有的低点,还引发了一场关于AI是否会彻底颠覆音乐行业的激烈讨论。从初期的兴奋到现在的理性审视࿰…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...
