深入理解二分法
前言
二分法(Binary Search)是一种高效的查找算法,广泛应用于计算机科学和工程领域。它用于在有序数组中查找特定元素,其时间复杂度为 O(log n),显著优于线性搜索的 O(n)。本文将深入介绍二分法的原理、实现及其应用场景,并提供一个详细的C语言实现示例。
二分法的基本思想
二分法通过将搜索空间逐步减半来定位目标值。其基本步骤如下:
- 初始化:定义搜索范围的起始点(left)和终点(right)。
- 查找中点:计算中间位置的索引(mid)。
- 比较中点值:将中点位置的值与目标值进行比较:
- 如果中点值等于目标值,则搜索成功。
- 如果中点值小于目标值,目标值必然位于中点右侧,将左边界更新为 mid + 1。
- 如果中点值大于目标值,目标值必然位于中点左侧,将右边界更新为 mid - 1。
- 重复步骤 2 和 3:直到找到目标值或搜索范围为空。
二分法的实现
以下是一个用C语言编写的二分法实现示例:
#include <stdio.h> // 二分查找函数 int binarySearch(int arr[], int size, int target) { int left = 0; int right = size - 1; while (left <= right) { int mid = left + (right - left) / 2; if (arr[mid] == target) { return mid; // 找到目标值,返回索引 } else if (arr[mid] < target) { left = mid + 1; // 目标值在右半部分 } else { right = mid - 1; // 目标值在左半部分 } } return -1; // 未找到目标值
}
int main() { int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; int size = sizeof(arr) / sizeof(arr[0]); int target = 7; int result = binarySearch(arr, size, target); if (result != -1) { printf("目标值 %d 在数组中的索引为 %d\n", target, result); } else { printf("目标值 %d 不在数组中\n", target); } return 0;
}示例解释
- 定义函数:
binarySearch函数接收三个参数:有序数组arr、数组大小size以及目标值target。 - 初始化:定义左右边界
left和right。 - 计算中点:在循环中计算中点索引
mid。 - 比较并调整边界:根据
arr[mid]与target的比较结果调整left或right。 - 返回结果:找到目标值返回索引,未找到返回 -1。
输出结果
目标值 7 在数组中的索引为 6二分法的应用场景
- 有序数组查找:二分法用于在有序数组中查找特定元素,如在词典中查找单词、数据库索引查找等。
- 二分查找变体:用于查找满足特定条件的最左或最右位置,如在排序数组中查找第一个大于等于某个值的元素。
- 数学求解:二分法可用于求解方程的根,如牛顿迭代法和黄金分割法等。
二分法的优缺点
优点
- 高效性:二分法的时间复杂度为 O(log n),在大数据集上比线性搜索更高效。
- 简单性:二分法算法逻辑简单,易于实现和理解。
缺点
- 有序要求:二分法要求数据是有序的,需先对数据进行排序,这可能会增加额外的时间开销。
- 适用范围:不适用于链表等非连续存储结构,因为无法直接访问中间元素。
总结
二分法是一种高效且广泛应用的搜索算法,适用于有序数据的查找。理解和掌握二分法,对于提升算法效率和解决实际问题具有重要意义。
相关文章:

深入理解二分法
前言 二分法(Binary Search)是一种高效的查找算法,广泛应用于计算机科学和工程领域。它用于在有序数组中查找特定元素,其时间复杂度为 O(log n),显著优于线性搜索的 O(n)。本文将深入介绍二分法的原理、实现及其应用场…...

【C命名规范】遵循良好的命名规范,提高代码的可读性、可维护性和可复用性
/******************************************************************** * brief param return author date version是代码书写的一种规范 * brief :简介,简单介绍函数作用 * param :介绍函数参数 * return:函数返回类型说明 * …...

Hbase面试题总结
一、介绍下HBase架构 --HMaster HBase集群的主节点,负责管理和协调整个集群的操作。它处理元数据和表的分区信息,控制RegionServer的负载均衡和故障恢复。--RegionServer HBase集群中的工作节点,负责存储和处理数据。每个RegionServer管理若…...

C语言部分复习笔记
1. 指针和数组 数组指针 和 指针数组 int* p1[10]; // 指针数组int (*p2)[10]; // 数组指针 因为 [] 的优先级比 * 高,p先和 [] 结合说明p是一个数组,p先和*结合说明p是一个指针 括号保证p先和*结合,说明p是一个指针变量,然后指…...
 : 用override set 设置工具链)
Rust学习笔记 (命令行命令) : 用override set 设置工具链
在cargo run某个项目时出现了如下错误:error: failed to run custom build command for ring v0.16.20(无法运行“Ring v0.16.20”的自定义构建命令),在PowerShell命令行运行命令 rustup override set stable-msvc后成功运行。 o…...

cv::Mat类的矩阵内容输出的各种格式的例子
操作系统:ubuntu22.04OpenCV版本:OpenCV4.9IDE:Visual Studio Code编程语言:C11 功能描述 我们可以这样使用:cv::Mat M(…); cout << M;,直接将矩阵内容输出到控制台。 输出格式支持多种风格,包括O…...

Redis--注册中心集群 Cluster 集群-单服务器
与“多服务器集群”一致需要创建redis配置模板 参照以下链接 CSDN 创建redis容器 node01服务器上创建容器 docker run -d --name redis-6381 --net host --privilegedtrue \ -v /soft/redis-cluster/6381/conf/redis.conf:/etc/redis/redis.conf \ -v /soft/redis-cluster/6…...
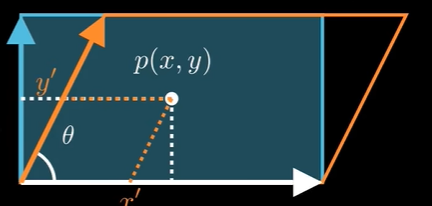
CV01_相机成像原理与坐标系之间的转换
目录 0.引言:小孔成像->映射表达式 1. 相机自身的运动如何表征?->外参矩阵E 1.1 旋转 1.2 平移 2. 如何投影到“像平面”?->内参矩阵K 2.1 图像平面坐标转换为像素坐标系 3. 三维到二维的维度是如何丢失的?…...
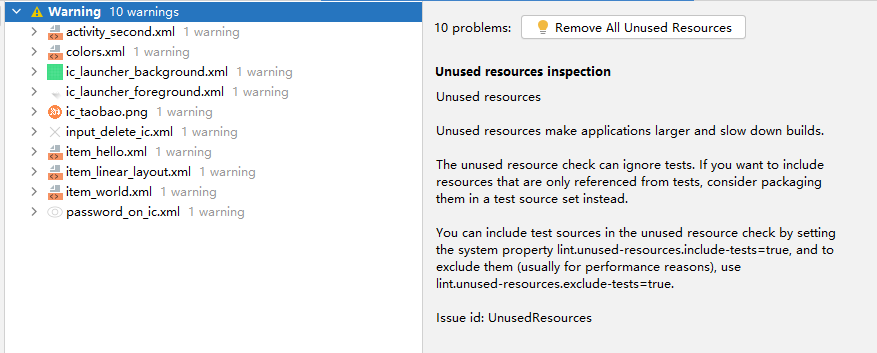
Android Lint
文章目录 Android Lint概述工作流程Lint 问题问题种类警告严重性检查规则 用命令运行 LintAndroidStudio 使用 Lint忽略 Lint 警告gradle 配置 Lint查找无用资源文件 Android Lint 概述 Lint 是 Android 提供的 代码扫描分析工具,它可以帮助我们发现代码结构/质量…...

【算法刷题 | 动态规划14】6.28(最大子数组和、判断子序列、不同的子序列)
文章目录 35.最大子数组和35.1题目35.2解法:动规35.2.1动规思路35.2.2代码实现 36.判断子序列36.1题目36.2解法:动规36.2.1动规思路36.2.2代码实现 37.不同的子序列37.1题目37.2解法:动规37.2.1动规思路37.2.2代码实现 35.最大子数组和 35.1…...
vue3 vxe-grid列中绑定vxe-switch实现数据更新
1、先上一张图: <template #valueSlot"{ row }"><vxe-switch :value"getV(row.svalue)" change"changeSwitch(row)" /></template>function getV(value){return value 1;};function changeSwitch(row) {console.l…...

Hive SQL:实现炸列(列转行)以及逆操作(行转列)
目录 列转行行转列 列转行 函数: EXPLODE(ARRAY):将ARRAY中的每一元素转换为每一行 EXPLODE(MAP):将MAP中的每个键值对转换为两行,其中一行数据包含键,另一行数据包含值 数据样例: 1、将每天的课程&#…...

MD5算法详解
哈希函数 是一种将任意输入长度转变为固定输出长度的函数。 一些常见哈希函数有:MD5、SHA1、SHA256。 MD5算法 MD5算法是一种消息摘要算法,用于消息认证。 数据存储方式:小段存储。 数据填充 首先对我们明文数据进行处理,使其…...

ES6的代理模式-Proxy
语法 target 要使用 Proxy 包装的目标对象(可以是任何类型的对象,包括原生数组,函数,甚至另一个代理handler 一个通常以函数作为属性的对象,用来定制拦截行为 const proxy new Proxy(target, handle)举个例子 <s…...

排序(堆排序、快速排序、归并排序)-->深度剖析(二)
前言 前面介绍了冒泡排序、选择排序、插入排序、希尔排序,作为排序中经常用到了算法,还有堆排序、快速排序、归并排序 堆排序(HeaSort) 堆排序的概念 堆排序是一种有效的排序算法,它利用了完全二叉树的特性。在C语言…...

七一建党节|热烈庆祝中国共产党成立103周年!
时光荏苒,岁月如梭。 在这热情似火的夏日, 我们迎来了中国共产党成立103周年的重要时刻。 这是一个值得全体中华儿女共同铭记和庆祝的日子, 也是激励我们不断前进的重要时刻。 103年, 风雨兼程,砥砺前行。 从嘉兴…...

Spring Boot应用知识梳理
一.简介 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的工具。它简化了基于 Spring 的应用程序的配置和部署过程,提供了一种快速、便捷的方式来构建独立的、生产级别的 Spring 应用程序。 Spring Boot 的一些主要优点包括: 1. 简化配置…...

Spring中利用重载与静态分派
Spring中利用重载与静态分派 在Java和Spring框架中,重载(Overloading)和静态分派(Static Dispatch)是两个非常重要的概念,它们在处理类方法选择和执行过程中扮演着关键角色。本文旨在深入探讨Spring环境下…...

文本三剑客之awk:
文本三剑客awk: grep 查 sed 增删改查 主要:增改 awk 按行取列 awk awk默认的分隔符:空格,tab键,多个空格自动压缩为一个。 awk的工作原理:根据指令信息,逐行的读取文本内容,然…...

SpringSecurity-授权示例
用户基于权限进行授权 定义用户与权限 authorities()。 package com.cms.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.security.core.userdetails.User; import…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
