盲信号处理的发展现状
盲源分离技术最早在上个世纪中期提出,在1991年Herault和Jutten提出基于反馈神经网络的盲源分离方法,但该方法缺乏理论基础,后来Tong和Liu分析了盲源分离问题的可辨识性和不确定性,Cardoso于1993年提出了基于高阶统计的联合对角化盲源分离方法,并应用于波束形成。
1994年Common将主分量法PCA加以扩展成为独立分量分析法,并正式提出了独立分量分析这一概念,提出了基于最小互信息量的独立分量分析方法。1995年Bell和Sejnowski提出了基于熵最大思想的盲源分离方法。1996年,B.A.Pearlmutter在独立变量分析(ICA)中引入以最大似然估计为准则的目标函数,提出了一种ICA的改进的算法。1997年,D.T.Pham和P.Garat对先前提出的基于最大似然准则的算法的性能进行进一步讨论。1997年Hyvariene等人根据峰度的概念提出了基于独立分量分析的快速分离算法FastICA。Armari于1998年提出了自然梯度算法口司,大大加快了算法的收敛速度。随着盲源分离的深入研究,研究范围不断拓展,一些学者开始研究相关源信号的盲分离问题,提出了时一频分析方法。2004年Yuan Zhijian和ErkkiOja提出了一种非独立分量分析的FastlCA算法。
参考文献
近年来,状态空间法得到了逐步的发展,它从控制工程的角度重新描述混合矩阵和解混矩阵,转换了盲源分离的研究思路。
[1] 徐宏. 语音盲分离算法及应用的研究[D]. 太原理工大学, 2011.
[2] 田其冲, 郑卫国, 孙大雷. 基于 FastICA 的语音分离与图像分离[J]. 电脑编程技巧与维护, 2009 (16): 90-91.
[3] 贾银洁, 许鹏飞. 基于 FastICA 的混合音频信号盲分离[J]. 信息与电子工程, 2009, 7(4): 321-325.
[4] Hyvärinen A, Oja E. Independent component analysis: algorithms and applications[J]. Neural networks, 2000, 13(4): 411-430.
[5] Hyvärinen A, Oja E. A fast fixed-point algorithm for independent component analysis[J]. Neural computation, 1997, 9(7): 1483-1492.
相关文章:

盲信号处理的发展现状
盲源分离技术最早在上个世纪中期提出,在1991年Herault和Jutten提出基于反馈神经网络的盲源分离方法,但该方法缺乏理论基础,后来Tong和Liu分析了盲源分离问题的可辨识性和不确定性,Cardoso于1993年提出了基于高阶统计的联合对角化盲…...
二轴机器人装箱机:重塑物流效率,精准灵活,引领未来装箱新潮流
在现代化物流领域,高效、精准与灵活性无疑是各大企业追求的核心目标。而在这个日益追求自动化的时代,二轴机器人装箱机凭借其较佳的性能和出色的表现,正逐渐成为装箱作业的得力助手,引领着未来装箱新潮流。 一、高效:重…...
使用python做飞机大战
代码地址: 点击跳转...

Python面向对象编程:派生
本套课在线学习视频(网盘地址,保存到网盘即可免费观看): https://pan.quark.cn/s/69d1cc25d4ba 面向对象编程(OOP)是一种编程范式,它通过将数据和操作数据的方法封装在一起࿰…...
华为仓颉编程语言
目录 一、引言 二、仓颉编程语言概述 三、技术特征 四、应用场景 五、社区支持 六、结论与展望 一、引言 随着信息技术的快速发展,编程语言作为软件开发的核心工具,其重要性日益凸显。近年来,华为公司投入大量研发资源,成功…...

【微信小程序开发实战项目】——如何制作一个属于自己的花店微信小程序(2)
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...

解锁数据资产的无限潜能:深入探索创新的数据分析技术,挖掘其在实际应用场景中的广阔价值,助力企业发掘数据背后的深层信息,实现业务的持续增长与创新
目录 一、引言 二、创新数据分析技术的发展 1、大数据分析技术 2、人工智能与机器学习 3、可视化分析技术 三、创新数据分析技术在实际应用场景中的价值 1、市场洞察与竞争分析 2、客户细分与个性化营销 3、业务流程优化与风险管理 4、产品创新与研发 四、案例分析 …...

Bridging nonnull in Objective-C to Swift: Is It Safe?
Bridging nonnull in Objective-C to Swift: Is It Safe? In the world of iOS development, bridging between Objective-C and Swift is a common practice, especially for legacy codebases (遗留代码库) or when integrating (集成) third-party libraries. One importa…...

算法训练 | 图论Part1 | 98.所有可达路径
目录 98.所有可达路径 深度搜索法 98.所有可达路径 题目链接:98. 所有可达路径 文章讲解:代码随想录 深度搜索法 代码一:邻接矩阵写法 #include <iostream> #include <vector> using namespace std; vector<vector<…...

【JVM基础篇】垃圾回收
文章目录 垃圾回收常见内存管理方式手动回收:C内存管理自动回收(GC):Java内存管理自动、手动回收优缺点 应用场景垃圾回收器需要对哪些部分内存进行回收?不需要垃圾回收器回收需要垃圾回收器回收 方法区的回收代码测试手动调用垃圾回收方法Sy…...
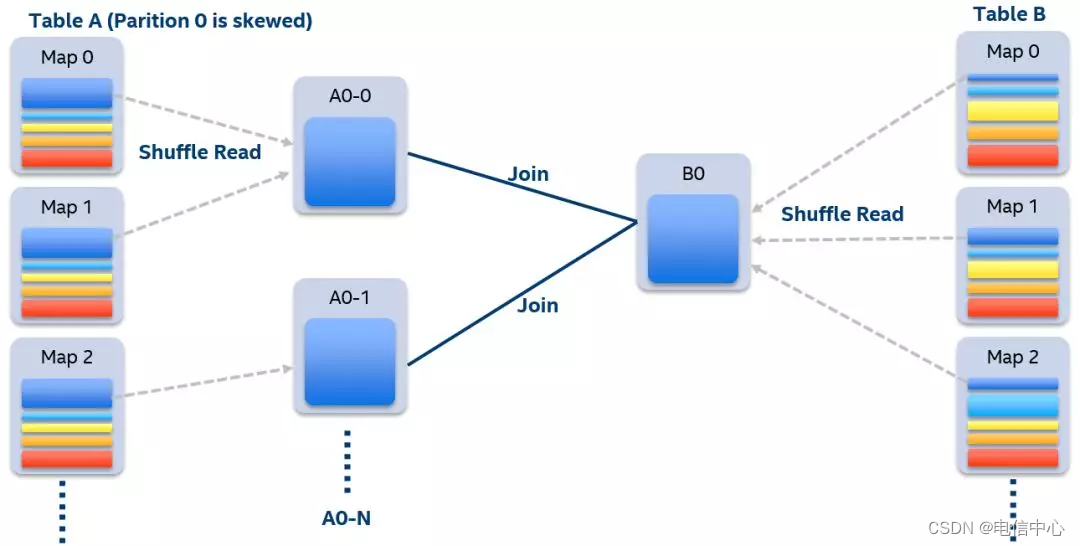
Spark join数据倾斜调优
Spark中常见的两种数据倾斜现象如下 stage部分task执行特别慢 一般情况下是某个task处理的数据量远大于其他task处理的数据量,当然也不排除是程序代码没有冗余,异常数据导致程序运行异常。 作业重试多次某几个task总会失败 常见的退出码143、53、137…...

YOLOv5初学者问题——用自己的模型预测图片不画框
如题,我在用自己的数据集训练权重模型的时候,在训练完成输出的yolov5-v5.0\runs\train\exp2目录下可以看到,在训练测试的时候是有输出描框的。 但是当我引用训练好的best.fangpt去进行预测的时候, 程序输出的图片并没有描框。根据…...
【linux学习---1】点亮一个LED---驱动一个GPIO
文章目录 1、原理图找对应引脚2、IO复用3、IO配置4、GPIO配置5、GPIO时钟使能6、总结 1、原理图找对应引脚 从上图 可以看出, 蜂鸣器 接到了 BEEP 上, BEEP 就是 GPIO5_IO05 2、IO复用 查找IMX6UL参考手册 和 STM32一样,如果某个 IO 要作为…...

Redis分布式锁代码实现详解
引言 在分布式系统中,资源竞争和数据一致性问题常常需要通过锁机制来解决。Redis作为一个高性能的键值存储系统,因其提供的原子操作、丰富的数据结构以及网络延迟低等特点,成为了实现分布式锁的理想选择。本文将详细介绍如何使用Redis来实现…...
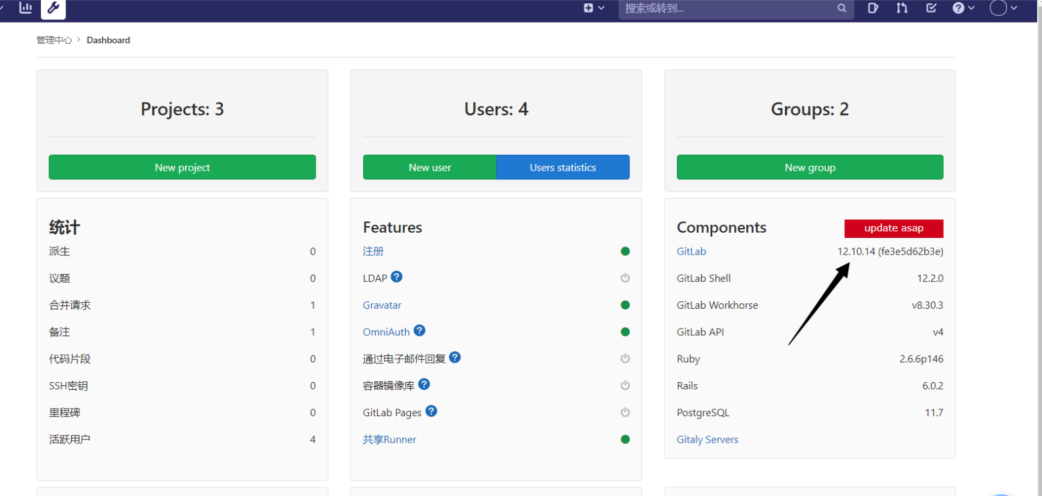
Day01-02-gitlab
Day01-02-gitlab 1. 什么是gitlab2. Gitlab vs Github/Gitee3. Gitlab 应用场景4. 架构5. Gitlab 快速上手指南5.0 安装要求5.1 安装Gitlab组件5.3 配置访问url5.6 初始化5.8 登录与查看5.9 汉化5.10 设置密码5.11 目录结构5.12 删除5.13 500 vs 5025.14 重置密码 6. Gitlab用户…...

PyCharm远程开发配置(2024以下版本)
目录 PyCharm远程开发配置 1、清理远程环境 1.1 点击Setting 1.2 进入Interpreter 1.3 删除远程环境 1.4 删除SSH 2、连接远程环境 2.1 点击Close Project 2.2 点击New Project 2.3 项目路径设置 2.4 SSH配置 2.5 选择python3解释器在远程环境的位置 2.6 配置远程…...

解决Ucharts在小程序上的层级过高问题
<qiun-wx-ucharts canvas2d"{{true}}" type"pie" opts"{{rectificationRateOpts}}" chartData"{{rectificationRateData}}" /> 开启2d渲染即可解决(在小程序开发工具上看着层级还是高,但是在手机上是正常…...

重保期间的网站安全防护:网站整站锁的应用与实践
标题:重保期间的网站安全防护:网站整站锁的应用与实践 一、引言 在重大活动或事件(通常被称为“重保”)期间,网站的安全问题尤为突出。由于此时网站的访问量和关注度可能达到高峰,因此也成为了黑客攻击的…...

Qt自定义类型
概述 在使用Qt创建用户界面时,特别是那些具有特殊控件和特性的界面时,开发人员有时需要创建新的数据类型,以便与Qt现有的值类型集一起使用或代替它们。 QSize、QColor和QString等标准类型都可以存储在QVariant对象中,作为基于qo…...
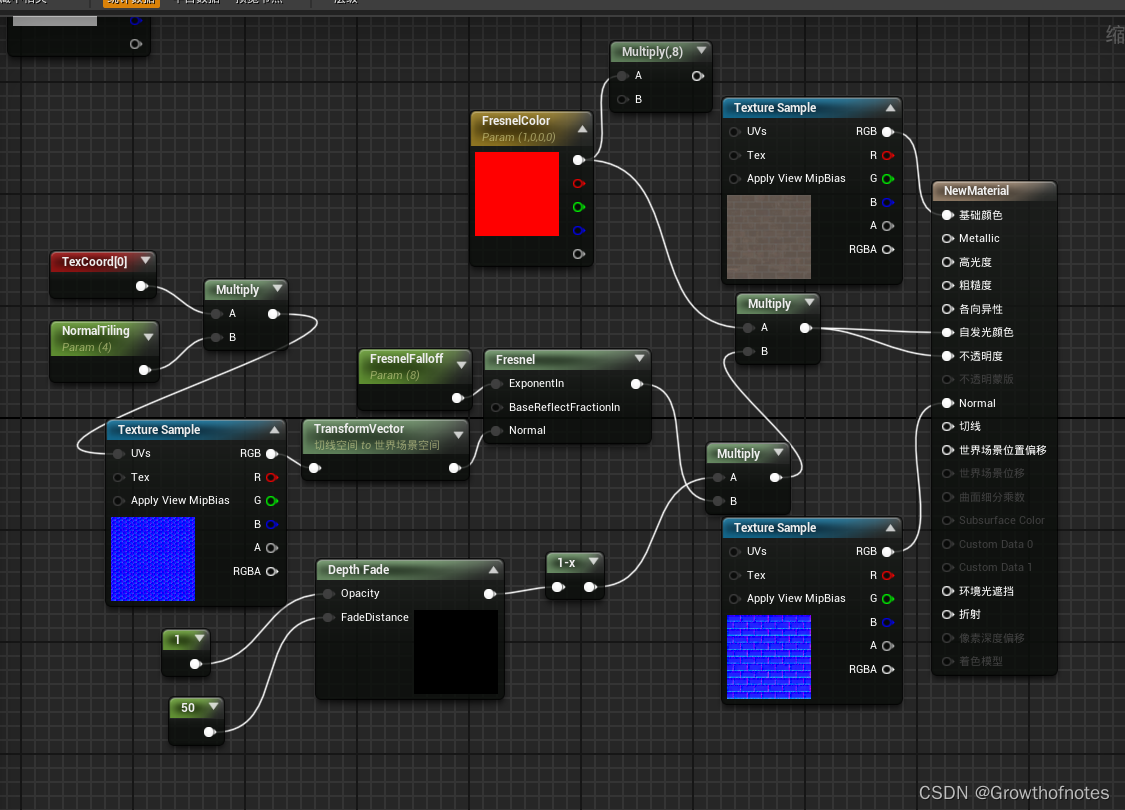
UE4_材质_材质节点_DepthFade
一、DepthFade参数 DepthFade(深度消退)表达式用来隐藏半透明对象与不透明对象相交时出现的不美观接缝。 项目说明属性消退距离(Fade Distance)这是应该发生消退的全局空间距离。未连接 FadeDistance(FadeDistance&a…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
