矩阵的奇异值(Singular Values)
矩阵的奇异值(Singular Values)是奇异值分解(SVD)过程中得到的一组重要特征值。它们在许多应用中非常重要,如信号处理、数据压缩和统计学等。以下是对奇异值及其计算和性质的详细解释:
奇异值分解(SVD)
奇异值分解是矩阵分解的一种方法,它将任意一个实数或复数矩阵分解为三个特定矩阵的乘积。具体来说,对于一个 m × n m \times n m×n的矩阵 M \mathbf{M} M,其奇异值分解表示为:
M = U Σ V ⊤ \mathbf{M} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top M=UΣV⊤
其中:
- U \mathbf{U} U是一个 m × m m \times m m×m的正交矩阵,包含了矩阵 M \mathbf{M} M的左奇异向量。
- Σ \mathbf{\Sigma} Σ是一个 m × n m \times n m×n的对角矩阵,对角线上是矩阵 M \mathbf{M} M的奇异值,其余元素为零。
- V ⊤ \mathbf{V}^\top V⊤是一个 n × n n \times n n×n的正交矩阵,包含了矩阵 M \mathbf{M} M的右奇异向量。
奇异值的计算
奇异值 σ i \sigma_i σi是矩阵 M \mathbf{M} M的奇异值分解中对角矩阵 Σ \mathbf{\Sigma} Σ的非负对角元素。它们是 M M ⊤ \mathbf{M} \mathbf{M}^\top MM⊤和 M ⊤ M \mathbf{M}^\top \mathbf{M} M⊤M的非负特征值的平方根。具体来说,如果 M \mathbf{M} M的奇异值为 σ i \sigma_i σi,那么 σ i \sigma_i σi满足以下条件:
M M ⊤ u i = σ i 2 u i \mathbf{M} \mathbf{M}^\top \mathbf{u}_i = \sigma_i^2 \mathbf{u}_i MM⊤ui=σi2ui
M ⊤ M v i = σ i 2 v i \mathbf{M}^\top \mathbf{M} \mathbf{v}_i = \sigma_i^2 \mathbf{v}_i M⊤Mvi=σi2vi
其中, u i \mathbf{u}_i ui和 v i \mathbf{v}_i vi分别是 M M ⊤ \mathbf{M} \mathbf{M}^\top MM⊤和 M ⊤ M \mathbf{M}^\top \mathbf{M} M⊤M的特征向量。
奇异值的性质
- 非负性:奇异值总是非负的,即 σ i ≥ 0 \sigma_i \geq 0 σi≥0。
- 排列顺序:奇异值通常按降序排列,即 σ 1 ≥ σ 2 ≥ ⋯ ≥ σ min ( m , n ) \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_{\min(m,n)} σ1≥σ2≥⋯≥σmin(m,n)。
- 数量:一个 m × n m \times n m×n矩阵最多有 min ( m , n ) \min(m, n) min(m,n)个奇异值。
- 对称性:奇异值是对称矩阵的特征值的绝对值。
奇异值的应用
奇异值在许多领域都有广泛应用,包括但不限于:
- 矩阵近似:通过截断较小的奇异值,可以得到矩阵的低秩近似,用于数据压缩和降维。
- 数据压缩:在图像处理和压缩中,保留较大的奇异值可以有效减少数据存储量,同时保持较高的数据质量。
- 信号处理:奇异值分解用于去噪和信号恢复。
- 统计学:在主成分分析(PCA)中,奇异值用于确定数据的主成分方向和方差。
通过以上解释,希望能帮助你更好地理解奇异值及其在矩阵分析中的重要性。
好的,让我们通过一个具体的例子来说明奇异值的计算过程。
示例矩阵
考虑一个 2 × 2 2 \times 2 2×2的矩阵 A \mathbf{A} A:
A = ( 3 1 1 3 ) \mathbf{A} = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} A=(3113)
计算奇异值
- 计算 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A和 A A ⊤ \mathbf{A} \mathbf{A}^\top AA⊤
首先,计算 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A和 A A ⊤ \mathbf{A} \mathbf{A}^\top AA⊤:
A ⊤ A = ( 3 1 1 3 ) ⊤ ( 3 1 1 3 ) = ( 10 6 6 10 ) \mathbf{A}^\top \mathbf{A} = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}^\top \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} = \begin{pmatrix} 10 & 6 \\ 6 & 10 \end{pmatrix} A⊤A=(3113)⊤(3113)=(106610)
A A ⊤ = ( 3 1 1 3 ) ( 3 1 1 3 ) ⊤ = ( 10 6 6 10 ) \mathbf{A} \mathbf{A}^\top = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}^\top = \begin{pmatrix} 10 & 6 \\ 6 & 10 \end{pmatrix} AA⊤=(3113)(3113)⊤=(106610)
注意到这两个矩阵是相同的。
- 求解 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A的特征值
接下来,求解 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A的特征值。设 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A的特征值为 λ \lambda λ,我们需要解特征方程:
det ( A ⊤ A − λ I ) = 0 \det(\mathbf{A}^\top \mathbf{A} - \lambda \mathbf{I}) = 0 det(A⊤A−λI)=0
即:
det ( 10 − λ 6 6 10 − λ ) = 0 \det\begin{pmatrix} 10 - \lambda & 6 \\ 6 & 10 - \lambda \end{pmatrix} = 0 det(10−λ6610−λ)=0
计算行列式:
( 10 − λ ) 2 − 36 = 0 (10 - \lambda)^2 - 36 = 0 (10−λ)2−36=0
解这个二次方程:
λ 2 − 20 λ + 64 = 0 \lambda^2 - 20\lambda + 64 = 0 λ2−20λ+64=0
求解得到特征值:
λ = 16 和 λ = 4 \lambda = 16 \quad \text{和} \quad \lambda = 4 λ=16和λ=4
- 计算奇异值
奇异值是 A \mathbf{A} A的特征值的平方根。因此:
σ 1 = 16 = 4 \sigma_1 = \sqrt{16} = 4 σ1=16=4
σ 2 = 4 = 2 \sigma_2 = \sqrt{4} = 2 σ2=4=2
因此,矩阵 A \mathbf{A} A的奇异值为 σ 1 = 4 \sigma_1 = 4 σ1=4和 σ 2 = 2 \sigma_2 = 2 σ2=2。
奇异值分解
我们可以进一步进行奇异值分解(SVD),将矩阵 A \mathbf{A} A分解为:
A = U Σ V ⊤ \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top A=UΣV⊤
其中:
- U \mathbf{U} U和 V \mathbf{V} V是正交矩阵(包含左奇异向量和右奇异向量)。
- Σ \mathbf{\Sigma} Σ是对角矩阵,包含奇异值。
对于本例中的矩阵 A \mathbf{A} A:
Σ = ( 4 0 0 2 ) \mathbf{\Sigma} = \begin{pmatrix} 4 & 0 \\ 0 & 2 \end{pmatrix} Σ=(4002)
计算 U \mathbf{U} U和 V \mathbf{V} V
左奇异向量 U \mathbf{U} U和右奇异向量 V \mathbf{V} V是通过求解以下方程得到的:
A A ⊤ u i = σ i 2 u i \mathbf{A} \mathbf{A}^\top \mathbf{u}_i = \sigma_i^2 \mathbf{u}_i AA⊤ui=σi2ui
A ⊤ A v i = σ i 2 v i \mathbf{A}^\top \mathbf{A} \mathbf{v}_i = \sigma_i^2 \mathbf{v}_i A⊤Avi=σi2vi
我们已知:
A A ⊤ = A ⊤ A = ( 10 6 6 10 ) \mathbf{A} \mathbf{A}^\top = \mathbf{A}^\top \mathbf{A} = \begin{pmatrix} 10 & 6 \\ 6 & 10 \end{pmatrix} AA⊤=A⊤A=(106610)
求解这两个矩阵的特征向量即可得到 U \mathbf{U} U和 V \mathbf{V} V。
通过计算,得到:
u 1 = v 1 = ( 1 2 1 2 ) , u 2 = v 2 = ( − 1 2 1 2 ) \mathbf{u}_1 = \mathbf{v}_1 = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix}, \quad \mathbf{u}_2 = \mathbf{v}_2 = \begin{pmatrix} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} u1=v1=(2121),u2=v2=(−2121)
因此:
U = V = ( 1 2 − 1 2 1 2 1 2 ) \mathbf{U} = \mathbf{V} = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} U=V=(2121−2121)
综上,矩阵 A \mathbf{A} A的奇异值分解为:
A = U Σ V ⊤ = ( 1 2 − 1 2 1 2 1 2 ) ( 4 0 0 2 ) ( 1 2 1 2 − 1 2 1 2 ) \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 4 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} A=UΣV⊤=(2121−2121)(4002)(21−212121)
这就是矩阵 A \mathbf{A} A的奇异值计算和奇异值分解的完整过程。
相关文章:
)
矩阵的奇异值(Singular Values)
矩阵的奇异值(Singular Values)是奇异值分解(SVD)过程中得到的一组重要特征值。它们在许多应用中非常重要,如信号处理、数据压缩和统计学等。以下是对奇异值及其计算和性质的详细解释: 奇异值分解…...
清空flowable的表定义的相关表
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 http://218.75.87.38:9666/ 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: h…...

Tailwind CSS 在vue里 的使用
在Vue项目中使用Tailwind CSS,你需要按照以下步骤操作: 安装Tailwind CSS npm包: npm install -D tailwindcss postcss autoprefixer 使用Tailwind CSS CLI工具创建配置文件: npx tailwindcss init -p 3.在tailwind.config.js中…...

【人工智能】--强化学习(2.0)
个人主页:欢迎来到 Papicatch的博客 课设专栏 :学生成绩管理系统 专业知识专栏: 专业知识 文章目录 🍉强化学习与有监督学习的区别 🍈数据特点 🍈学习目标 🍈反馈机制 🍈策略…...

跟着峰哥学java 微信小程序 第二天 封装ES7 + 后端工作
1.前端 1.1使用promise封装 使用promise封装以至于在图片路径 统一路径中修改 //封装统一请求域名 const baseUrl "http://localhost:8080"; //封装后需导出 export const getBaseUrl()>{return baseUrl; } 导入外来资源 初始化数据 设置数据 将处理后的数据…...

QT学习(6)——QT中的定时器事件,两种实现方式;事件的分发event,事件过滤器
目录 引出定时器事件QTimerEventQTimer 事件的分发事件过滤器 总结QT中的鼠标事件定义QLable的鼠标进入离开事件提升为myLabel重写QLabel的函数鼠标的事件鼠标的左中右键枚举鼠标多事件获取和鼠标移动鼠标追踪 QT中的信号和槽自定义信号和槽1.自定义信号2.自定义槽3.建立连接4.…...

ASP.NET Core 6.0 使用 Action过滤器
Action过滤器 在ASP.NET Core中,Action过滤器用于在执行Action方法之前或之后执行逻辑。你可以创建自定义的Action过滤器来实现这一点。 继承 ActionFilterAttribute 类: [TypeFilter(typeof(CustomAllActionResultFilterAttribute))]public IActionRe…...
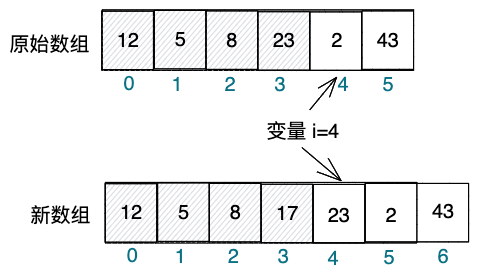
Java 并发集合:CopyOnWrite 写时复制集合介绍
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 016 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

Linux 查看修改系统时间| date -s
Linux 查看修改系统时间 date 命令的介绍date基本语法date命令使用示例显示指定条件的时间设置指定条件的时间时间加减操作显示文件最后修改时间显示 UTC 时间 备注 date 命令的介绍 date 命令在 Linux/Unix 系统上的使用。 date 命令可以用于查看和设置系统时间。 date基本语…...

数据库MySQL学习笔记
数据库MySQL学习笔记 主要记录常见的MySQL语句学习过程,增删改查。 -- 显示所有数据库 SHOW DATABASES;-- 创建新数据库 CREATE DATABASE mydatabase;-- 使用数据库 USE mydatabase;-- 显示当前数据库中的所有表 SHOW TABLES;-- 创建新表 CREATE TABLE users (id …...

四端口千兆以太网交换机与 SFP 扩展功能
在数字化时代,网络基础设施的重要性日益凸显,它是企业和个人取得成功的关键支撑。配备 SFP 插槽的 4 端口千兆以太网交换机提供了一种灵活且可扩展的网络解决方案,能够应对快速的数据传输、低延迟以及不断增长的带宽需求。本篇文章深入探讨了…...

Renderless 思想正在影响前端开发
本文由前端小伙伴方长_beezen 原创。欢迎大家踊跃投稿。 原文链接:https://juejin.cn/post/7385752495535472655 前言 截止到 2024 年,跨端应用开发所需要考虑的兼容性,已经涵盖了框架、平台和设备类型等多个方面,例如࿱…...
maven 打包执行配置(对maven引用的包或者丢进去的包都包含在里面)打成jar包
一 、springboot jar包 maven的pom文件 1 在resources下放了一些文件想打进去jar包 2 在lib下放了其他稀奇古怪jar包文件想打进去jar包 编写如下引入jar <build><!-- 打包名称 --><finalName>${project.artifactId}</finalName><resources><…...

Python酷库之旅-第三方库Pandas(004)
目录 一、用法精讲 5、pandas.DataFrame.to_csv函数 5-1、语法 5-2、参数 5-3、功能 5-4、返回值 5-5、说明 5-6、用法 5-6-1、代码示例 5-6-2、结果输出 6、pandas.read_fwf函数 6-1、语法 6-2、参数 6-3、功能 6-4、返回值 6-5、说明 6-6、用法 6-6-1、代码…...

天猫超市卡怎么用
猫超卡是在天猫超市里面消费用的卡 但是我们现在买东西都喜欢货比三家,肯定是哪家划算在哪买,要是淘宝其他店铺或京东卖的更便宜,猫超卡自然就用不上了 这种情况的话,还不如直接把猫超卡的余额提出来,买东西也不受限…...

ai智能语音机器人电销系统:让销售更快速高效
智能机器人电销系统是指采用人工智能和机器人技术来实现的自动电销工具。随着企业竞争加剧,销售团队面临的挑战也越来越大。在人力资源和成本控制方面有很大的限制,而传统的电销方式也已经无法满足市场需求,因此需要一种新的解决方案来提高营…...

Redis 中的通用命令(命令的返回值、复杂度、注意事项及操作演示)
Redis 中的通用命令(高频率操作) 文章目录 Redis 中的通用命令(高频率操作)Redis 的数据类型redis-cli 命令Keys 命令Exists 命令Expire 命令Ttl 命令Type命令 Redis 的数据类型 Redis 支持多种数据类型,整体来说,Redis 是一个键值对结构的,…...

【Hive实战】 HiveMetaStore的指标分析
HiveMetaStore的指标分析(一) 文章目录 HiveMetaStore的指标分析(一)背景目标部署架构 hive-site.xml相关配置元数据服务的指标相关配置 源码部分(hive2.3系)JvmPauseMonitor.javaHiveMetaStore的内部类HMS…...

【Linux系统】CUDA的安装与graspnet环境配置遇到的问题
今天在安装环境时遇到报错: The detected CUDA version (10.1) mismatches the version that was used to compile PyTorch (11.8). Please make sure to use the same CUDA versions. 报错原因:安装的cuda版本不对应,我需要安装cuda的版本…...
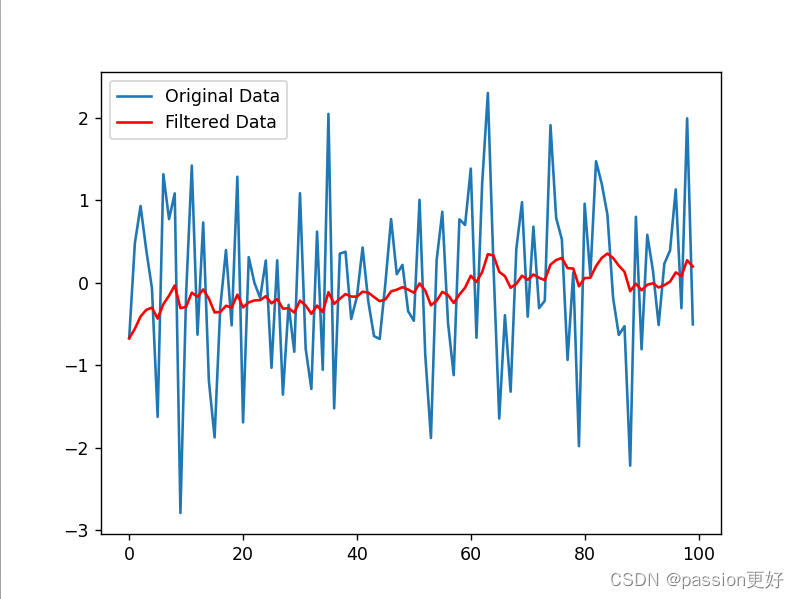
滤波算法学习笔记
目录 引言 一、定义 二、分类 三、常见滤波算法 四、应用与优势 五、发展趋势 例程 1. 均值滤波(Moving Average Filter) 2. 中值滤波(Median Filter) 3. 高斯滤波(Gaussian Filter) 4.指数移动…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
