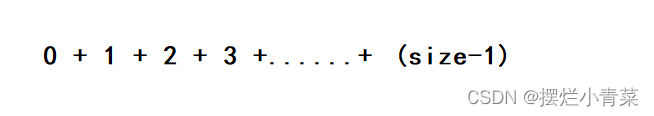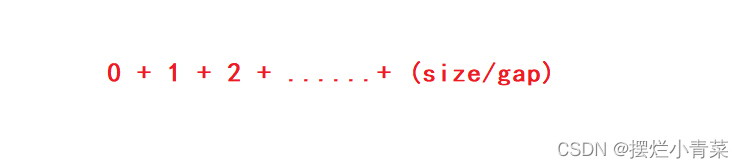八大排序算法之插入排序+希尔排序
目录
一.前言(总体简介)
关于插入排序
关于希尔排序:
二.插入排序
函数首部:
算法思路:
算法分析
插入排序代码实现:
插入排序算法的优化前奏:
三.希尔排序(缩小增量排序)
1.算法思想:
2.算法拆分解析
序列分组
分组预排序:
分组预排序的另一种实现方式:
希尔排序的实现思路(这里采用Knuth实现法)
关于gap指数式递减的分析:
四.希尔排序的时间复杂度分析
分组预排序的时间复杂度
gap指数式递减过程中,多次分组预排序的总复杂度分析:
经典数据结构书目中对希尔排序复杂度的说明:
五.实测对比希尔排序与普通插入排序的时间效率
一.前言(总体简介)
关于插入排序
- 插入排序的思想:将各元素逐个插入到已经有序的序列中的指定位置
- 插入排序的思想很类似于我们玩扑克牌时逐张摸牌并整理牌序的方式:
- 还有一个更贴近算法实现的gif:
- 将上面的方条看成数组中的元素
- 橙色的方条代表已经排好序的元素序列,蓝色的方条代表待插入的各元素
- 在算法实现中,橙色的方条构成的序列用一个下标变量来维护(每次循坏该下标变量加1)
关于希尔排序:
- 希尔排序是插入排序的优化版本,优化算法由希尔本人给出
- 基本思想是先对数组的子数组(按照一定规则划分而成)进行预排序,使待排序数组变得相对有序,最后再对整个数组进行一次插入排序完成整体的排序
二.插入排序
函数首部:
void InsertSort(DataType* arr, int size);
- arr是待排序数组首地址指针;
- size是待排序的元素个数;
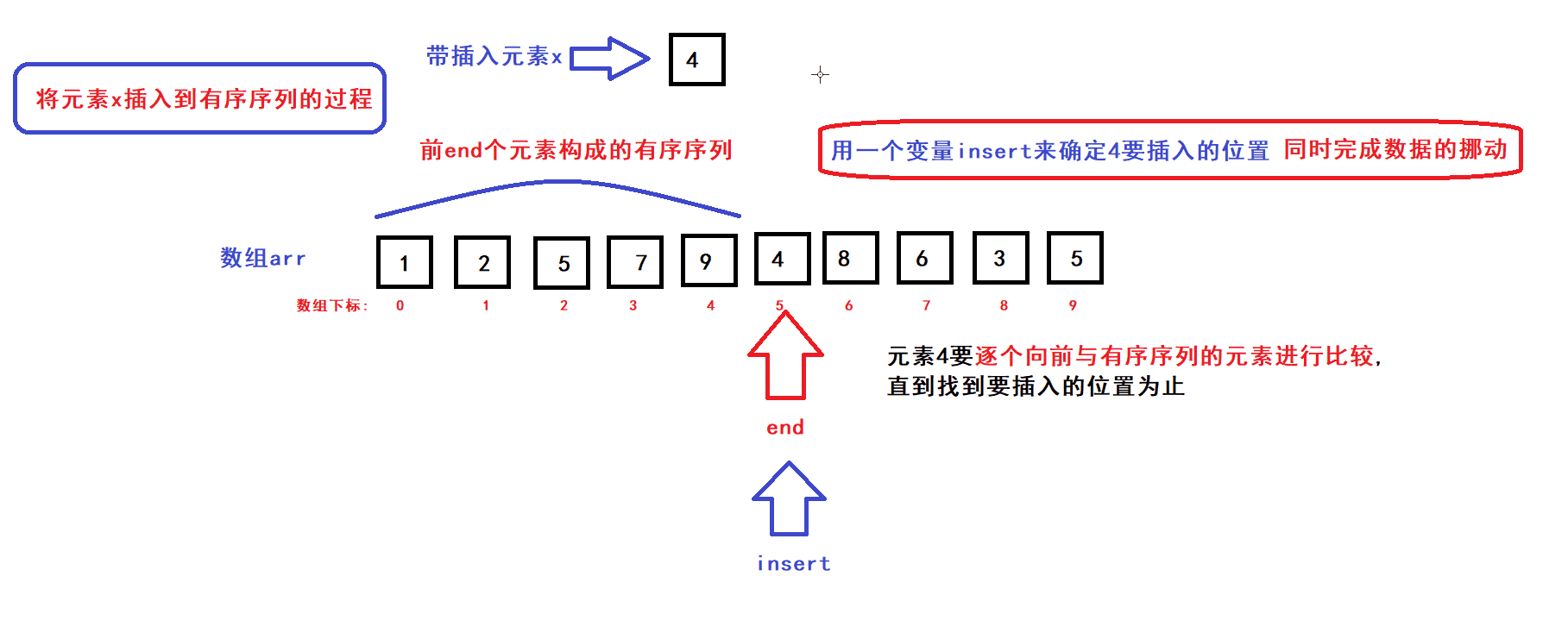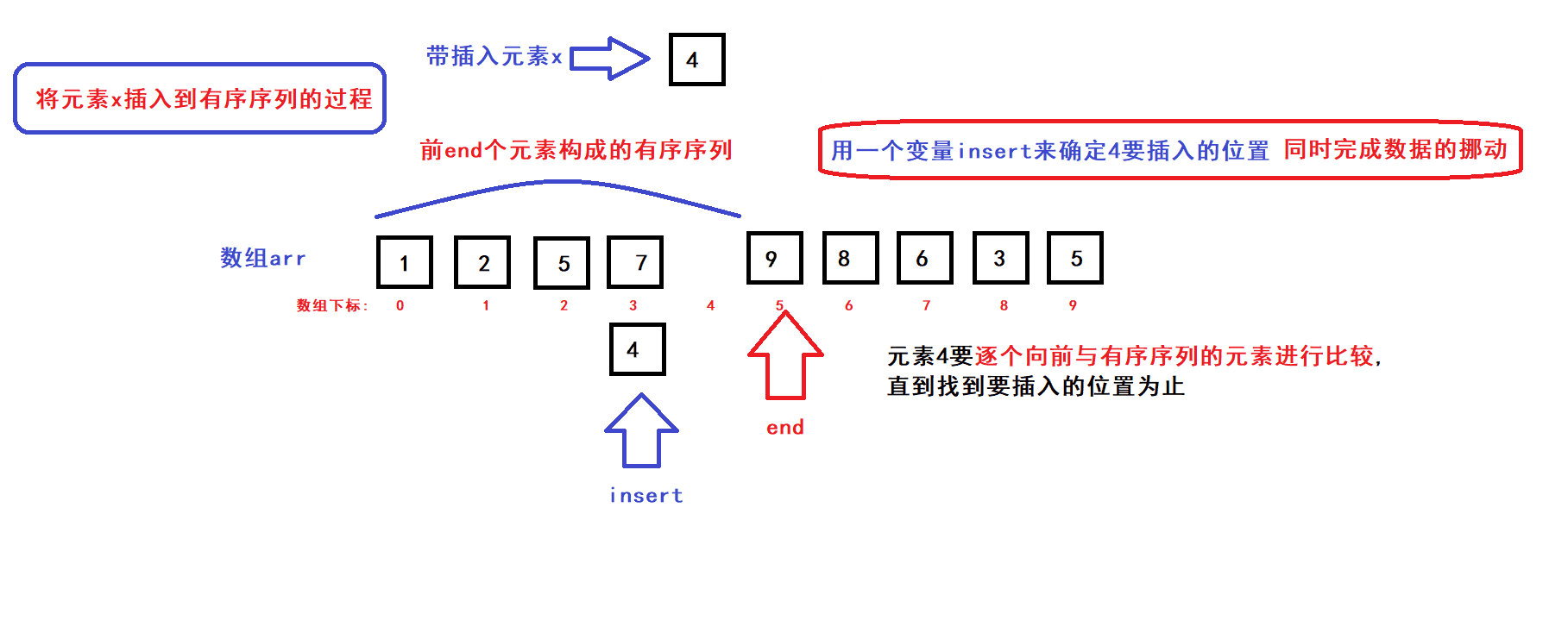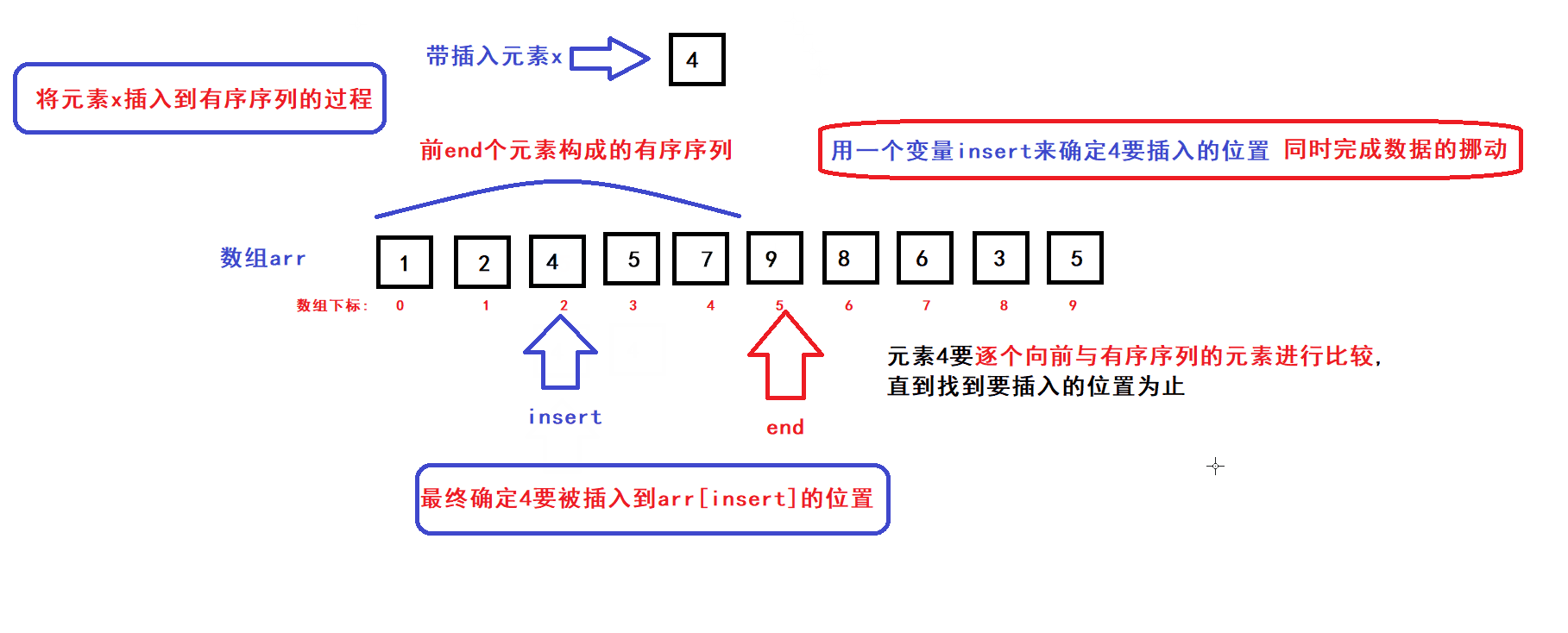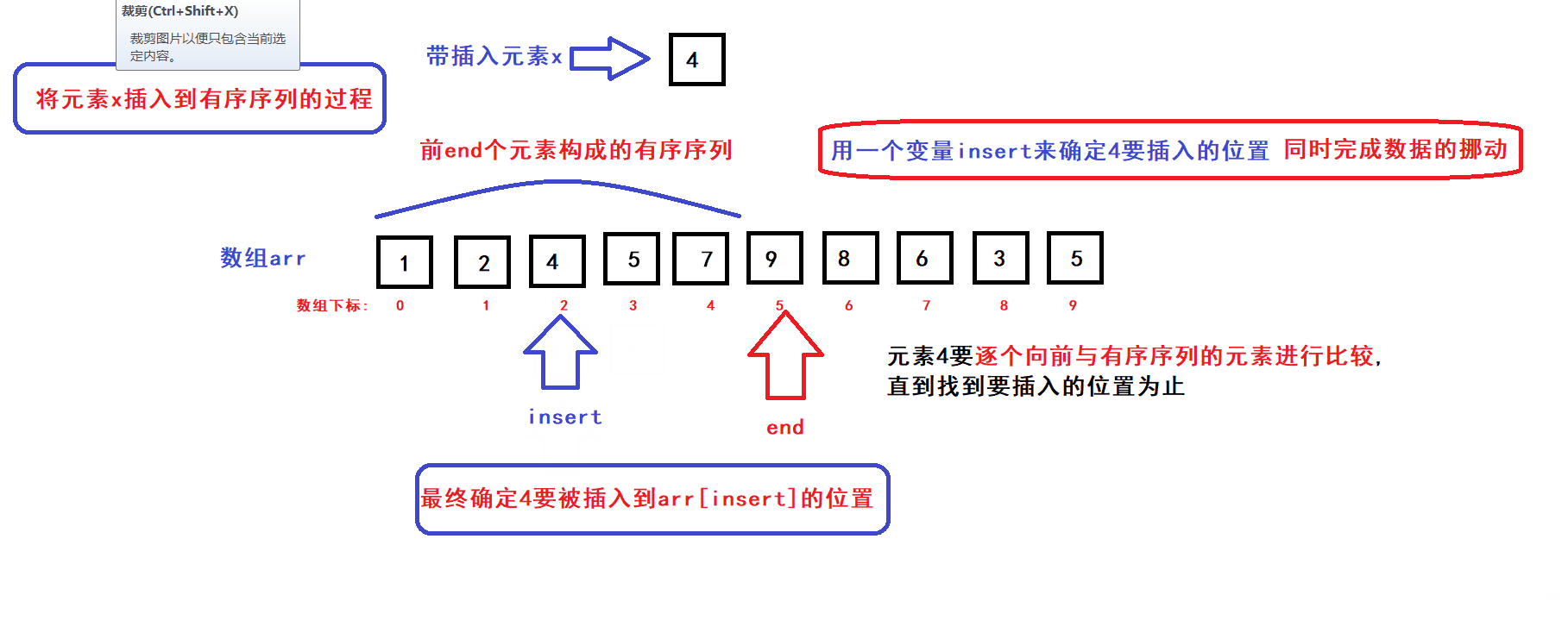
算法思路:
- 用一个数组下标变量end来维护前end个有序元素(end初始化为0)
- 每个循环过程中,将end下标变量指向的元素插入到前end个元素中的某个指定位置上构成一个end+1个元素的有序序列,然后end加一,接着执行下一次循环直到end遍历完整个数组后循环结束;
- 每次循环过程中,x元素插入的位置是通过元素比较来确定的:
- end为0时,有序序列元素个数为0;end为1时,有序序列的元素个数为1........;当end为size时,有序序列的元素个数便为size(即数组中size个元素按序排列)此时排序完成
- 插入排序便是以这种递推的方式将数组arr调整成有序序列的
算法分析
- 从算法思路中可以看到,完成一个元素x插入到前end个元素构成的有序序列的过程中,会发生数据的比较和挪动
- 在最坏的情况下,每完成一个元素x插入到前end个元素的构成的有序序列的过程中,有序序列的每个元素都要被往后挪动一个位置(即元素比较和挪动的次数为end次)
- 因此整个排序的过程中发生元素的比较和挪动的总次数为:
- 所以插入排序的时间复杂度为:O(N^2) (N为待排序的元素个数);
插入排序代码实现:
两层循环实现:
- 外层循环用end控制(有size个元素要插入,循环size次)(每次要插入前缀序列的元素x=arr[end])(end下标遍历了整个数组)
for(int end =0;end<size;++end)内层循环用insert控制,用于比较和挪动数据,确定x要插入的位置并完成插入(insert每次从end开始递减直到等于0或者刚好找到x要插入的位置)
以排升序为例:
//以排升序为例 void InsertSort(DataType* arr, int size) {assert(arr);for (int end = 0; end < size; end++) //用end来维护数组前end个元素构成的有序序列{int x = arr[end]; //x为待插入有序序列的数据int insert = end; //用变量insert来确定x要插入的位置while (insert>0) //通过元素比较确定x要插入的位置{if (x < arr[insert-1]) //说明insert不是x要插入的位置{arr[insert] = arr[insert-1]; //往后挪动数据为x留出空位insert--; //令insert指向序列前一个元素}else{break; //有序序列中x>=arr[insert-1]说明insert是x要插入的位置}} //最坏的情况下x会被插入到数组的首地址处(此时数据比较和挪动了end次)arr[insert] = x; //完成元素x的插入(继续插入下一个元素)} }
- 注意算法的边界条件:
- 外层循环end增加到size时结束循环(数组各元素下标为0到size-1)
- 内层循环insert等于0时说明x比前end个元素的有序序列中的所有元素都小,x将被插入到数组下标为insert=0的位置
插入排序算法的优化前奏:
- 插入排序算法利用了逐个元素递推插入前缀有序数列的方法完成整个待排序序列的调整(元素插入的过程中,前缀序列有序的性质有时可以大大减少元素的比较和挪动次数).
- 因此插入排序算法有一个特点:当待排序数组arr整体相对有序时,排序过程的时间复杂度接近O(N),举个例子:
- 插入排序在处理上图的序列过程中元素总的比较次数为size+2次,元素总的挪动次数为3次(总体上可以认为:在处理整体上大致有序的序列时,插入排序的时间复杂度与size是线性相关的);
- 插入排序的上述特点为算法的优化提供了可能,如果我们能够在对序列正式进行插入排序之前,让序列整体上变得相对有序,那么就可以降低排序时间复杂度的数量级,这就是希尔排序诞生的思想起点
三.希尔排序(缩小增量排序)
- 希尔排序算法由大神D.L.Shell于1959年提出而得名,其本质上是在插入排序的基础上进行优化而产生的
先给出排序接口的首部:
void ShellSort(DataType* arr, int size);
- DataType为typedef定义的元素类型
- size是待排序数组arr中的元素个数
1.算法思想:
- 经过对插入排序的分析我们已经知道:在处理整体上大致有序的序列时,插入排序的时间复杂度与待排序元素个数是线性相关的
- 因此在正式进行插入排序之前,我们考虑先将序列进行多次分组预排序
- 多次分组预排序完成后,整体序列将变得相对有序,最后再进行一次插入排序完成整体序列的排序
2.算法拆分解析
序列分组
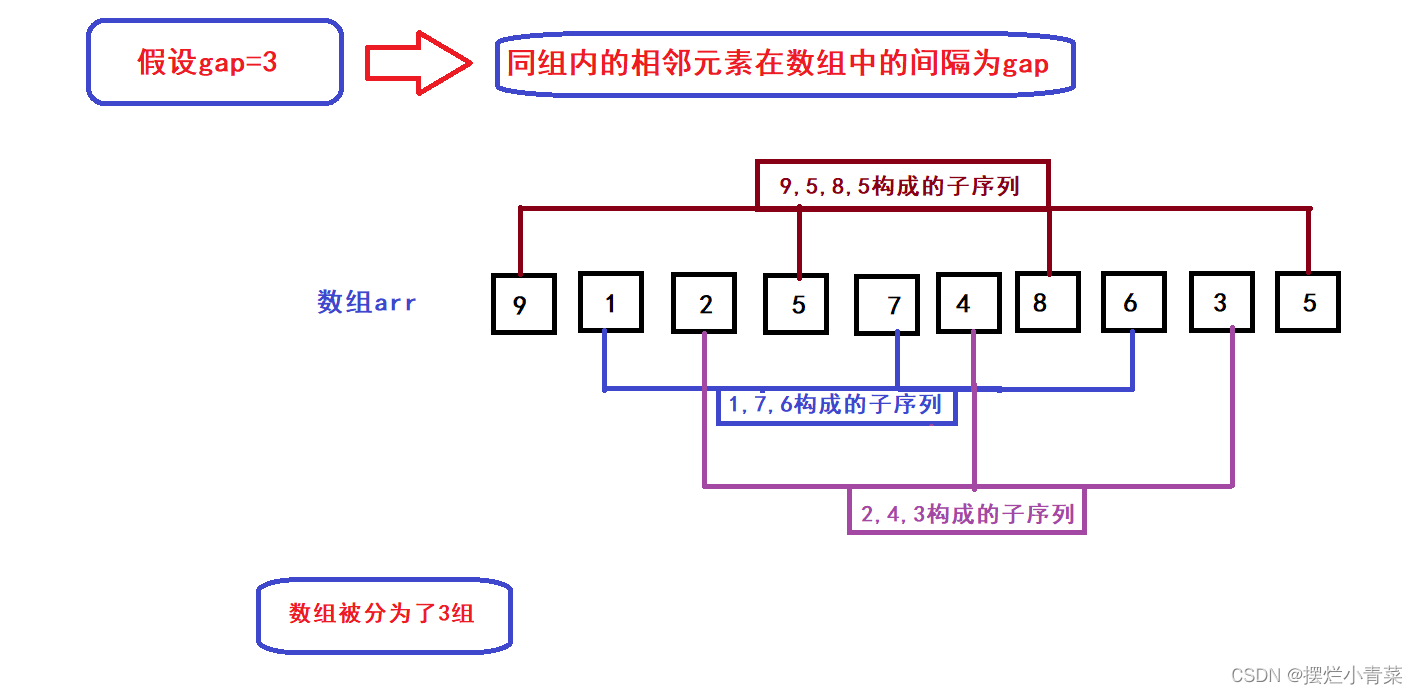
- 序列分组方式图文解析:先确定一个gap值(gap<=size)(将序列划分为gap组),从数组第一个元素开始以gap为间隔构成子序列,如图所示:
- 根据上述分组方式,我们简单地进行数学上的分析:由于gap<=size,因此我们一定可以将数组arr分为gap个子序列(每个子序列的元素个数至少为(size/gap)个;当size为gap整数倍时,每个子序列的元素个数为(size/gap)个,当size不为gap整数倍时,每个子序列元素个数最大为(size/gap)+1个);(以上数学表达式中的除法皆为向下取整除法)
- 我给这种序列分组模式取个名字:序列固定间隔分组法
- 序列固定间隔分组法的另外一种图示形式:
- 可见每个子序列的首元素分别为下标为0到gap-1的元素
- 完成了序列的固定间隔分组后,接下来就要对这些子序列分别进行插入排序,即分组预排序
分组预排序:
- 确定了gap值后,对各个子序列分别进行插入排序:(图示中以gap=3为例子)
- 分组预排序的代码实现思路:(最基础的思路是三层循环实现)
- 数组arr被分为gap组, 所以要对gap个子序列进行插入排序即最外层循环gap次,最外层循环用start变量来控制(初始化为0),边界条件为start<gap;
- 内两层循环的代码架构与插入排序完全一致
- 分组预排序的代码实现(建立在插入排序代码的框架上):
void ShellSort(DataType* arr, int size) {assert(arr);int gap; //将数组划分为gap组(gap待定)for (int start = 0; start < gap; ++start) //start为每个子序列的首元素下标(gap个子序列循环gap次){for (int end = start; end < size; end += gap) //用end来维护子序列中的前缀有序序列(end不能大于或等于size)(end下标遍历了子序列){int x = arr[end]; //x为待插入前缀有序序列的元素int insert = end; //用insert确定x要插入的位置while (insert>start) //insert=start时说明x要插入到子序列首元素的位置{if (x < arr[insert - gap]) //说明insert不是x要插入的位置{arr[insert] = arr[insert - gap]; //挪动数据,为x空出位置insert -= gap; //指向子序列的前一个元素}else //x >= arr[insert - gap]说明insert就是x要插入的位置{ break;}}arr[insert] = x; //完成x元素的插入} } }代码段完成了一次分组预排序(分组间隔为gap)
代码段中如果gap等于1,分组预排序则变为普通的插入排序
分组预排序的另一种实现方式:
分组预排序可以用两层循坏来实现:
注:两层循环的分组预排序和三层循环的分组预排序其实本质上没有区别,只是元素调整顺序不一样(三层循环是一组接一组子序列完成插入排序,两层循环是逐个元素完成调整)
void ShellSort(DataType* arr, int size) {assert(arr);int gap; //gap值待定 for (int end = 0; end < size; ++end) //用end来遍历数组每一个元素{int x = arr[end]; //x为待插入子序列前缀的元素int insert = end; //用insert确定x要插入的位置while (insert >= gap) //insert<gap的时,insert为下标的元素不需要调整{if (x < arr[insert - gap]) //说明insert不是x要插入的位置{arr[insert] = arr[insert - gap]; //挪动数据,为x空出位置insert -= gap; //指向子序列的前一个元素}else //x >= arr[insert - gap]说明insert就是x要插入的位置{break;}}arr[insert] = x; //完成x元素的插入} }三层循环改为两层循环,其具体代码思路图解如下:
三层循环的写法和两层循环的写法本质都是完成了gap为某确定值时的一次分组预排序
同样地,代码段中如果gap等于1,分组预排序则变为普通的插入排序
后续为了简洁起见,我们采用两层循环的分组预排序实现法来完成希尔排序
希尔排序的实现思路(这里采用Knuth实现法)
- 由之前的分析我们可以知道:gap的值确定了序列的一个划分(序列被划分为gap个子序列),对这些子序列分别进行插入排序便完成了一次序列的分组预排序
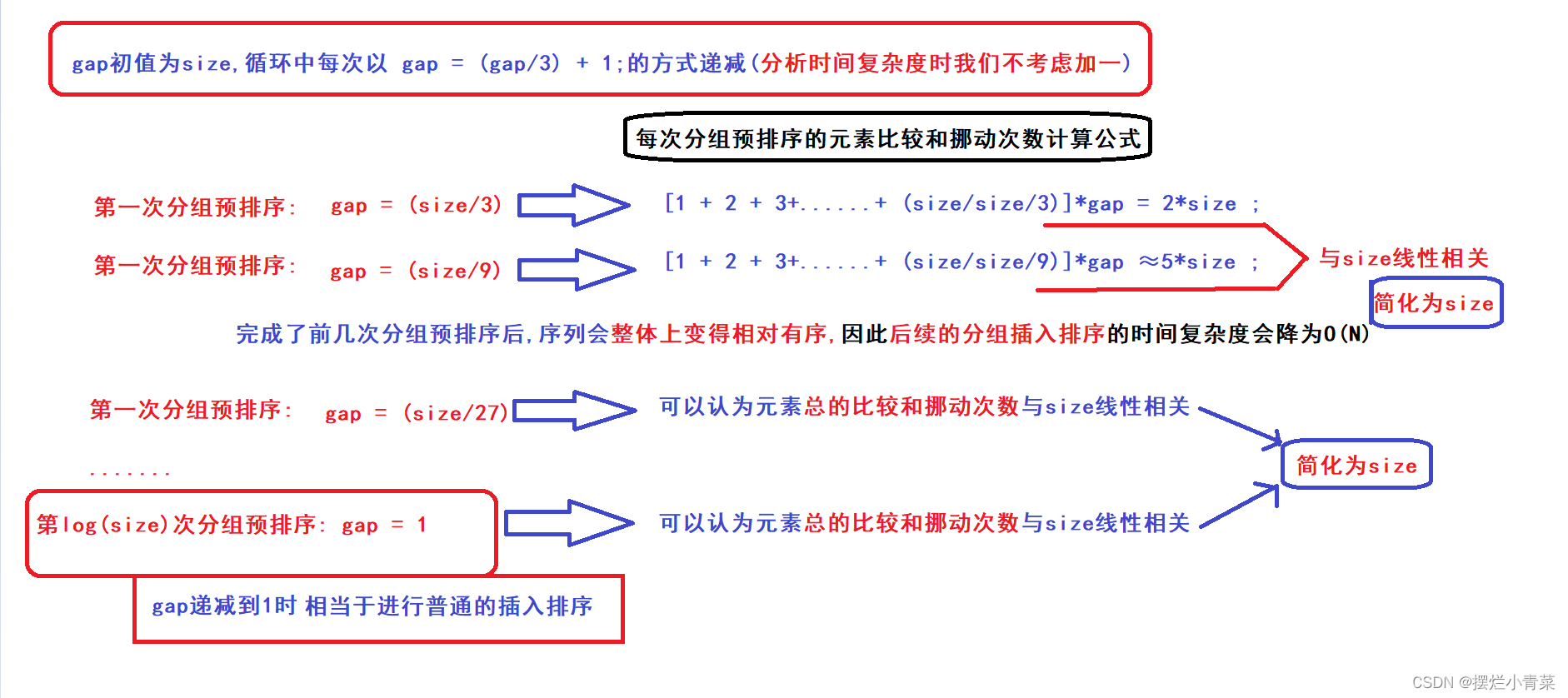
- 我们置gap的初始值为size,gap每次循环按照gap = (gap/3)+1的方式递减(由简单的数学分析可知gap一定会减小到1)(加1就是为了保证gap最终一定会减小到1)
- 对于每一个gap值我们都对待排序数组进行一次分组预排序
- 当gap减小到1时,数组已经经过了一次或多次分组预排序,最后再完成一次gap为1的分组预排序(gap为1时的分组预排序等价于普通的插入排序)从而完成数组整体的排序(gap为1的排序必须进行,否则不能保证整体序列一定有序)
- 我们只需在分组预排序的实现代码外层再套一层由gap控制的循环即可实现上述过程:
void ShellSort(DataType* arr, int size) {assert(arr);int gap = size; while (gap>1) //gap为1时序列已经完成了普通插入排序,排序完成{gap = gap/3 + 1; //缩小gap的值for (int end = 0; end < size; ++end) //用end来遍历数组每一个元素{int x = arr[end]; //x为待插入子序列前缀的元素int insert = end; //用insert确定x要插入的位置while (insert >= gap) //insert<gap的时,insert为下标的元素不需要调整{if (x < arr[insert - gap]) //说明insert不是x要插入的位置{arr[insert] = arr[insert - gap]; //挪动数据,为x空出位置insert -= gap; //指向子序列的前一个元素}else //x >= arr[insert - gap]说明insert就是x要插入的位置{break;}}arr[insert] = x; //完成x元素的插入}} }
关于gap指数式递减的分析:
- 希尔排序算法中,gap从size开始呈指数式递减. (这也是缩小增量排序这个名字的来源)
- 因此,算法中分组预排序的执行次数的数量级为(logN) (N=size)
- gap设计成指数式递减这一思想非常重要,这样既保证了在进行gap=1的插入排序之前,完成了一定次数的分组预排序,又保证了分组预排序的次数不会太多(分组预排序的次数如果太多反倒会降低算法整体的效率)
四.希尔排序的时间复杂度分析
希尔排序接口首部:
void ShellSort(DataType* arr, int size)
分组预排序的时间复杂度
序列分组图示:
- 为了方便分析,我们假设每次分组预排序,size都为gap的整数倍:根据序列固定间隔分组法,待排序数组被划分为gap个子序列,每个子序列元素个数为(size/gap)个
- 根据插入排序的时间复杂度计算公式:完成每组子序列的插入排序算法循环中元素比较和挪动的总次数的数量级为:
- 即完成一次分组预排序的时间复杂度计算表达式为:
gap指数式递减过程中,多次分组预排序的总复杂度分析:
- 可以发现一个规律:gap值越大(gap<=size)的分组预排序元素比较和挪动次数的上限就越低(复杂度越接近线性),因此利用较大的gap值进行分组预排序将总体序列调整为相对有序序列的设计非常巧妙!!!
- 将size写成N,则希尔排序的时间复杂度总体的数量级大致为NlogN
- 该证明并不严格,但是总体上反映出了希尔排序通过多次分组预排序的方法尝试降低整体排序的时间复杂度数量级的思想。
- 希尔大神设计该算法时,gap的递减方式是:gap=gap/2;
- gap = (gap/3)+1这种缩小增量的公式是由kunth大神给出的,希尔排序的最优gap递减公式目前尚未求得(这牵涉到一些尚未得到完全解决的数学难题)
经典数据结构书目中对希尔排序复杂度的说明:
以下文段摘自《数据结构-用面相对象方法与C++描述》--- 殷人昆
- gap的取法有多种.最初Shell提出取gap=gap/2,直到gap=1,后来Kunth提出取gap=(gap/3) +1.还有人提出都取奇数为好,也有人提出各gap互质为好.无论哪一种主张都没有得到证明。
- 对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算关键码的比较次数和对象移动次数,但想要弄清关键码比较次数和对象移动次数与增量选择之间的依赖关系,并给出完全的数学分析,还没有人能够做到。在Kunth所著的《计算机程序设计技巧》第三卷中,利用大量的实验数据统计资料得出,当n很大时,关键码平均比较次数和对象平均移动次数大约在n^1.25 到1.6n^1.25范围内,这是在利用直接插入排序作为子序列排序方法的情况下得到的
从上述文段中我们可以得知,受当前数学分析的限制,我们可以暂且根据Kunth大神的实验结果,将希尔排序的时间复杂度看成是: O(N^1.25)
五.实测对比希尔排序与普通插入排序的时间效率
- 利用随机数生成器创建两个十万个元素的相同整形数组,一个用直接插入排序进行排序,另外一个用希尔排序进行排序,打印出两者所消耗的时间(单位为毫秒)
int main() {srand(time(0));const int N = 100000;int* arr1 = (int*)malloc(sizeof(int) * N);int* arr2 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){arr1[i] = rand();arr2[i] = arr1[i];}int begin1 = clock();InsertSort(arr1, N);int end1 = clock();printf("IsertSort:%d\n", end1-begin1);int begin2 = clock();ShellSort(arr2, N);int end2 = clock();printf("ShellSort:%d\n", end2-begin2);return 0; }
可见希尔排序的算法优化思路虽然新奇复杂,但毫无疑问的是,希尔大神对插入排序所进行的优化是非常成功的!!!!(而且数据量越大希尔排序的优化效果就越明显)

相关文章:

八大排序算法之插入排序+希尔排序
目录 一.前言(总体简介) 关于插入排序 关于希尔排序: 二.插入排序 函数首部: 算法思路: 算法分析 插入排序代码实现: 插入排序算法的优化前奏: 三.希尔排序(缩小增量排序) 1.算法思想: 2.算法拆分解析 序列分组 分组预排序: 分组预排序的另一种实现方式: 希尔…...

蓝桥杯第十四届蓝桥杯模拟赛第三期考场应对攻略(C/C++)
这里把我的想法和思路写出来,恳请批评指正! 目录 考前准备 试题1: 试题2: 试题3: 试题4: 试题5: 试题6: 试题7: 试题8: 试题9: 试题1…...
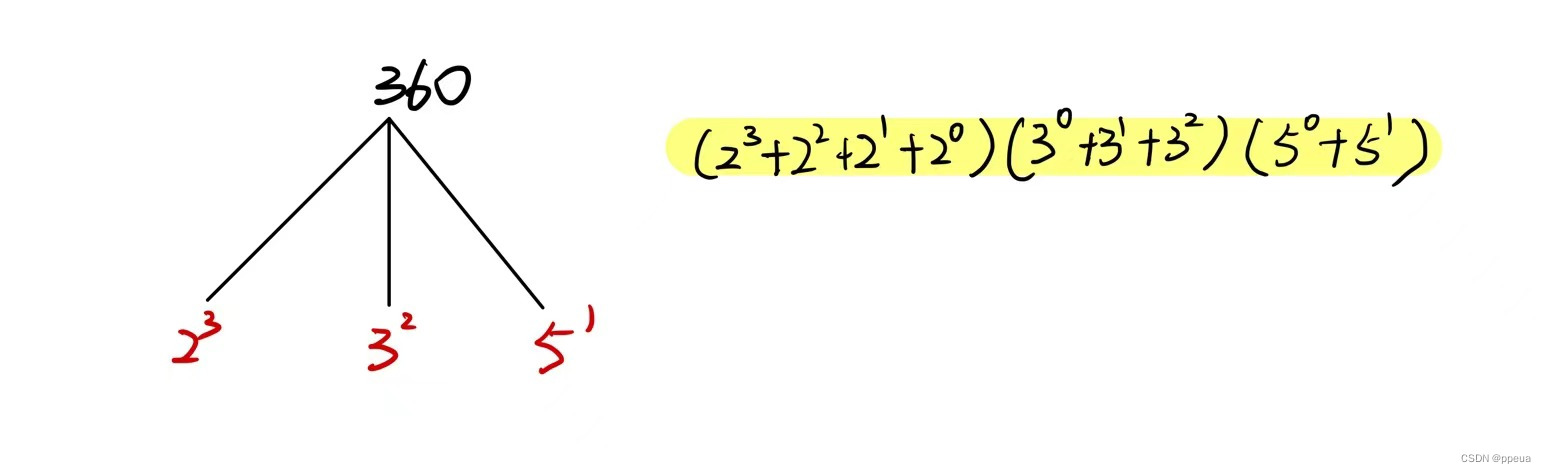
【数论】最大公约数、约数的个数与约数之和定理
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
)
第28篇:Java日期Calendar类总结(二)
目录 1、获取系统当前时间 2、获取指定日期 3、对象字段类型 4 、对象信息设置 4.1 Set设置...

【Python】字符串 - 集大成篇
目录 1. 不同语言的字符串比较 1.1 C 语言 1.2 C 语言 1.2.1 C 风格字符串 1.2.2 C 风格字符串 1.3 JAVA 1.4 Python 2. Python 字符串 2.1 方法 2.2.1 title () 2.2.2 lower () 2.2.3 upper () 2.2.4 rstrip () 2.2.5 lstrip …...

IDEA: 如何导入项目模块 以及 将 Java程序打包 JAR 详细步骤
IDEA: 如何导入项目模块 以及 将 Java程序打包 JAR 详细步骤 、 文章目录IDEA: 如何导入项目模块 以及 将 Java程序打包 JAR 详细步骤IDEA 导入项目模块 Module一. 创建一个空项目二. 导入 Module三. 将 Module 与 当前项目关联上IDEA 将 Java程序打包成…...
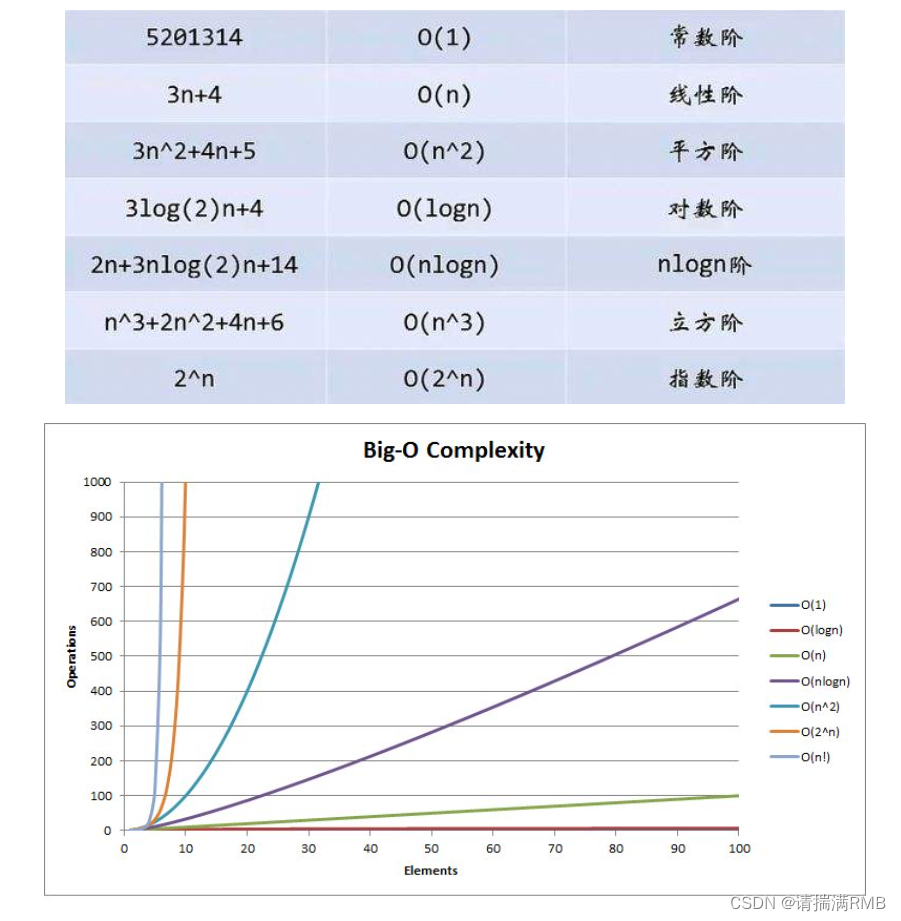
算法的效率——时间复杂度和空间复杂度
文章目录1. 算法效率1.1 什么是算法1.2 算法的好坏2. 时间复杂度2.1 什么是时间复杂度2.2 时间复杂度的计算方法2.3 大O的渐进表示法2.4 常见时间复杂度计算举例3. 空间复杂度4. 常见复杂度对比1. 算法效率 1.1 什么是算法 目前普遍认可对算法的定义是:算法是解决…...

2021年 第12届 蓝桥杯 Java B组 省赛真题详解及小结【第1场省赛 2021.04.18】
总分:5 一、试题A:ASC 得分:5分 本题总分:5 分 【问题描述】 已知大写字母 A 的 ASCII 码为 65,请问大写字母 L 的 ASCII 码是多少? 【答案提交】 这是一道结果填空的题,你只需要算出结果后提…...
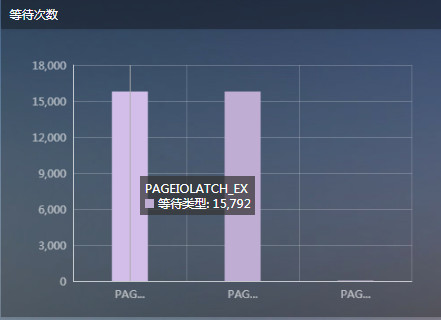
透过等待看数据库
等待分类与解决基本流程步骤1.定位问题系统等待往往能直观的反映出系统问题。通过一些常见的等待类型,同样可以找到系统瓶颈,结合性能计数器往往定位更准确。如:系统中存在大量IO类等待,那么可能表示你的磁盘或内存是语句运行缓慢…...
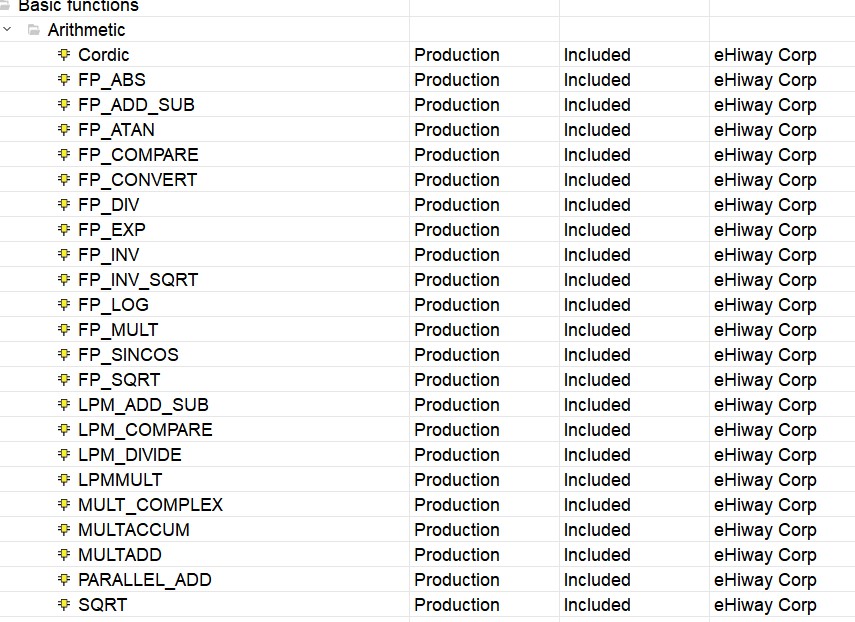
中科亿海微FPGA
国产FPGA中,紫光、安路、高云称得上是三小龙,其他的半斤八两,中科亿海微也算是其中之一。 其产品为亿海神针系列,如下: 可见其最小规模也有9.2KLUT,最大竟有136K之多了,对比其他国产࿰…...

【链表OJ题(三)】链表中倒数第k个结点
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(三)1. 链表…...

华为防火墙的学习
防火墙 - 含义和定义 什么是防火墙? 防火墙的工作原理 防火墙的区域: 包过滤防火墙----访问控制列表技术---三层技术 代理防火墙----中间人技术---应用层 状态防火墙---会话追踪技术---三层、四层 UTM---深度包检查技术----应用层 下一代防火墙 防火墙的…...
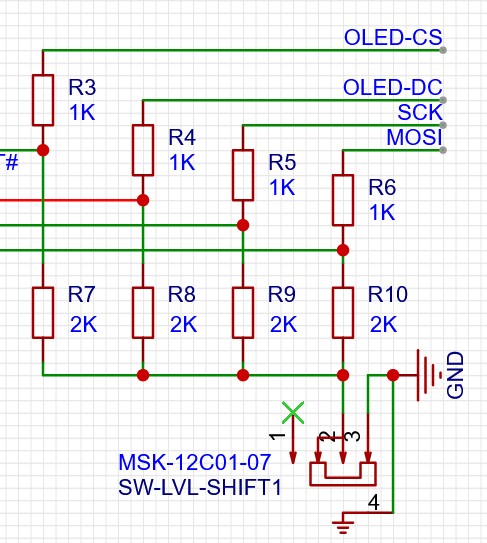
SPI 接口OLED 模块 - 兼容5V 和3.3V 电平
PCB 布局参考了老王0.8元128x32OLED显示屏转接板,开源项目地址:老王0.8元128x32OLED。 老王家买的屏幕放了快一年了,终于还是决定整个单独的模块,之前一直打算集成到开发板上的,不太灵活。相比那个转接板,主…...

css布局和定位
在Web开发中,CSS布局和定位是非常重要的技能。在这篇博客中,我们将深入探讨CSS布局和定位的概念、基本技术和最佳实践。 **CSS布局基础** ├── 盒模型 │ ├── 内边距 │ │ ├── padding │ │ ├── padding-top │ │ ├── p…...
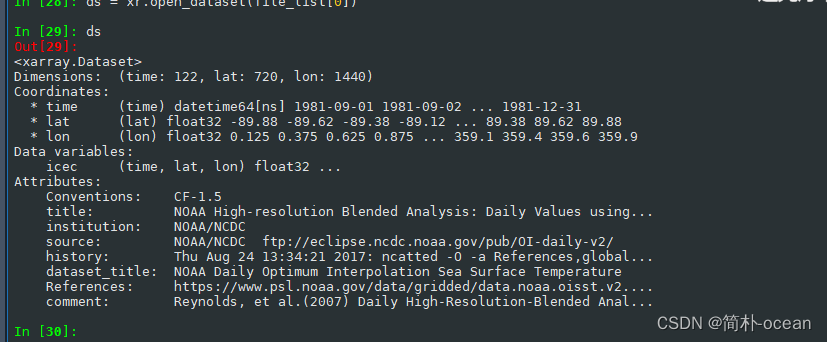
python -- 批量读取多个文件,并将每个文件中相同变量累加
python – 批量读取多个文件,并将每个文件中相同变量累加 情况描述 现有多个nc文件,位于同一个文件夹中,如下所示每个文件中都有相同的变量,想要读取每个文件中的变量然后将其加起来意思就是说: 文件1中的变量文件2中…...

低代码开发流程是怎么样的?
低代码开发流程是怎么样的?现在很多文章都在下功夫宣传what(低代码是什么)、why(为什么要用低代码),但是很少有文章能够系统讨论how(怎么用低代码)的问题。 所以我花3天的时间准备了…...

任何时候都不要在 for 循环中删除 List 集合元素!!!
首先说结论:无论什么场景,都不要对List使用for循环的同时,删除List集合元素,因为这么做就是不对的。 阿里开发手册也明确说明禁止使用foreach删除、增加List元素。 正确删除元素的方式是使用迭代器(Iteratorÿ…...

koa+Vite+vue3+ts+pinia构建项目
一、 初始化构建项目 npm create vite myProject -- --template vue-ts 注:Vite 需要 Node.js 版本 14.18,16。然而,有些模板需要依赖更高的 Node 版本才能正常运行,当你的包管理器发出警告时,请注意升级你的 Node 版…...
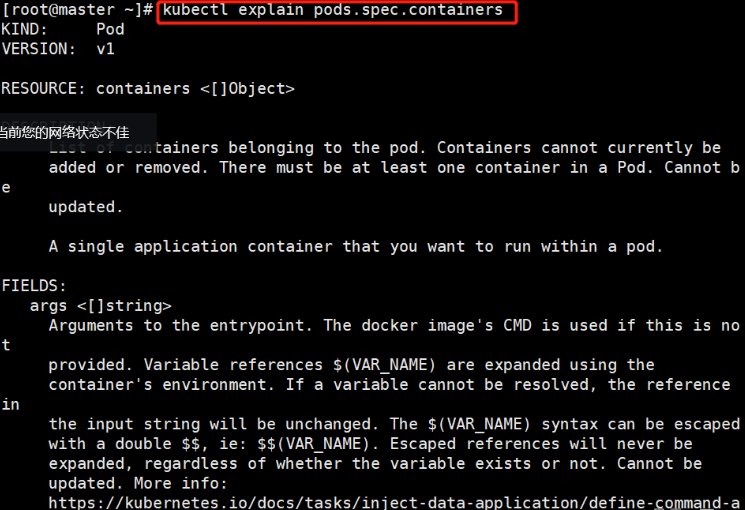
k8s-yaml文件
文章目录一、K8S支持的文件格式1、yaml和json的主要区别2、YAML语言格式二、YAML1、查看 API 资源版本标签2、编写资源配置清单2.1 编写 nginx-test.yaml 资源配置清单2.2 创建资源对象2.3 查看创建的pod资源3、创建service服务对外提供访问并测试3.1 编写nginx-svc-test.yaml文…...
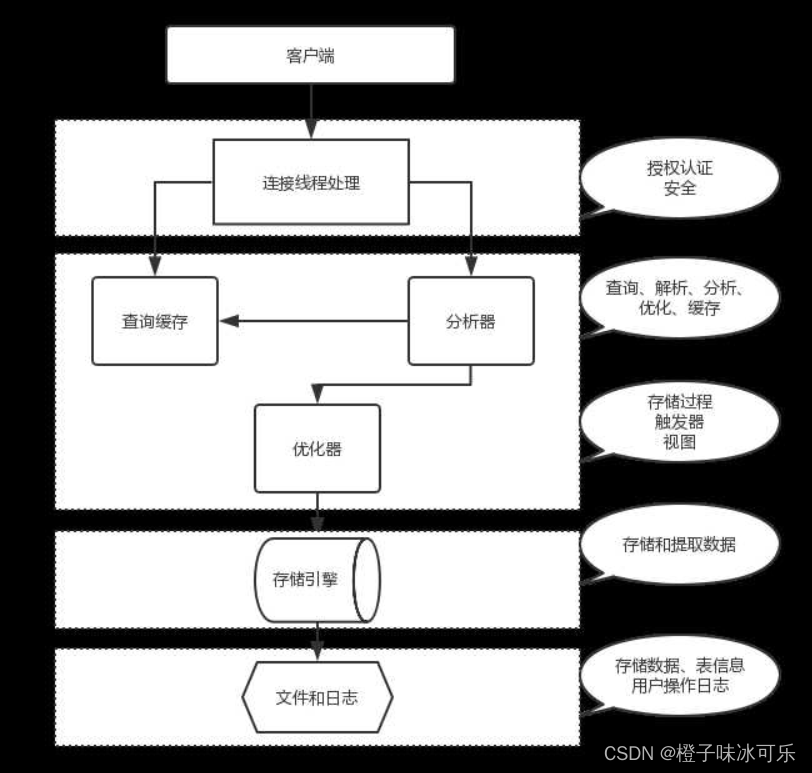
存储引擎
目录 ❤ MySQL存储引擎 什么是存储引擎? MySQL支持哪个存储引擎? ❤ 各种存储引擎的特性 概述 各种存储引擎的特性 各种搜索引擎介绍 ❤ 常用存储引擎及适用场景 ❤ 存储引擎在mysql中的使用 存储引擎相关sql语句 指定存储引擎建表 在建表时指定 在配置文件中…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

LTR-381RGB-01RGB+环境光检测应用场景及客户类型主要有哪些?
RGB环境光检测 功能,在应用场景及客户类型: 1. 可应用的儿童玩具类型 (1) 智能互动玩具 功能:通过检测环境光或物体颜色触发互动(如颜色识别积木、光感音乐盒)。 客户参考: LEGO(乐高&#x…...
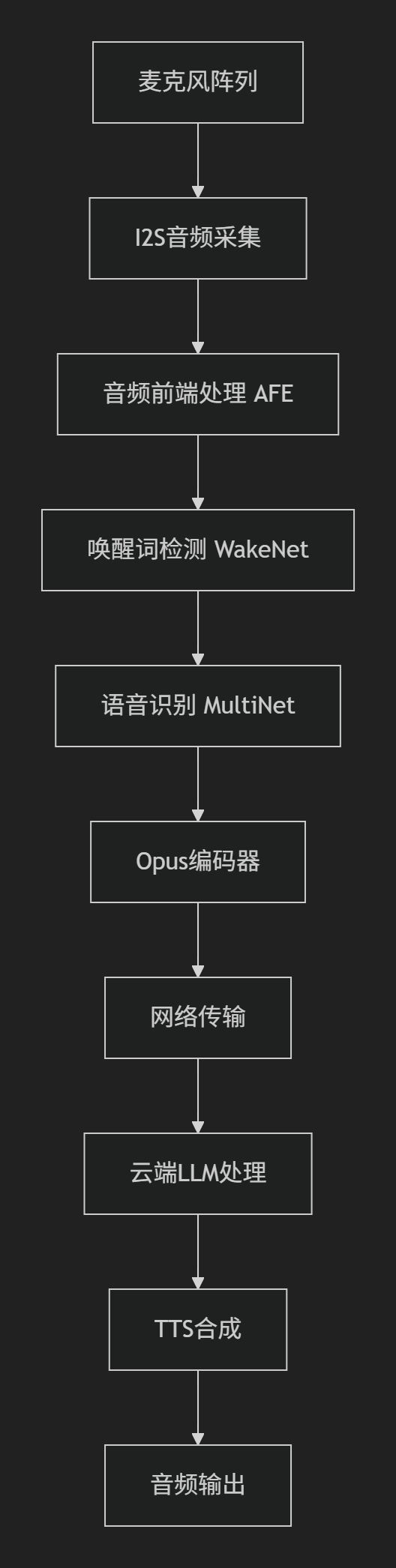
SDU棋界精灵——硬件程序ESP32实现opus编码
一、 音频处理框架 该项目基于Espressif的音频处理框架构建,核心组件包括 ESP-ADF 和 ESP-SR,以下是完整的音频处理框架实现细节: 1.核心组件 (1) 音频前端处理 (AFE - Audio Front-End) main/components/audio_pipeline/afe_processor.c功能: 声学回声…...

Clickhouse统计指定表中各字段的空值、空字符串或零值比例
下面是一段Clickhouse SQL代码,用于统计指定数据库中多张表的字段空值情况。代码通过动态生成查询语句实现自动化统计,处理逻辑如下: 从系统表获取指定数据库(替换your_database)中所有表的字段元数据根据字段类型动态…...