【拳打蓝桥杯】算法前置课——时间复杂度与空间复杂度

文章目录
- 前言
- 为什么需要复杂度分析?
- 大O复杂度表示法
- 时间复杂度分析
- 几种常见时间复杂度实例分析
- 空间复杂度分析
- 内容小结
- 最后说一句
🐱🐉作者简介:大家好,我是黑洞晓威,一名大二学生,希望和大家一起进步。
👿本文收录于 算法,本专栏是针对大学生、初学算法的人准备,解析常见的数据结构与算法,同时备战蓝桥杯。

前言
我们都知道,数据结构和算法本身解决的是“快”和“省”的问题,即如何让代码运行得更快,如何让代码更省存储空间。所以,执行效率是算法一个非常重要的考量指标。那如何来衡量你编写的算法代码的执行效率呢?这里就要用到我们今天要讲的内容:时间、空间复杂度分析。
其实,只要讲到数据结构与算法,就一定离不开时间、空间复杂度分析。而且,, 复杂度分析是整个算法学习的精髓,只要掌握了它,数据结构和算法的内容基本上就掌握了一半。
为什么需要复杂度分析?
你可能会有些疑惑,我把代码跑一遍,通过统计、监控,就能得到算法执行的时间和占用的内存大小。为什么还要做时间、空间复杂度分析呢?这种分析方法能比我实实在在跑一遍得到的数据更准确吗?
首先,我可以肯定地说,你这种评估算法执行效率的方法是正确的。很多数据结构和算法书籍还给这种方法起了一个名字,叫 事后统计法。但是,这种统计方法有非常大的局限性。
1. 测试结果非常依赖测试环境
测试环境中硬件的不同会对测试结果有很大的影响。比如,我们拿同样一段代码,分别用Intel Core i9处理器和Intel Core i3处理器来运行,不用说,i9处理器要比i3处理器执行的速度快很多。还有,比如原本在这台机器上a代码执行的速度比b代码要快,等我们换到另一台机器上时,可能会有截然相反的结果。
2.测试结果受数据规模的影响很大
后面我们会讲排序算法,我们先拿它举个例子。对同一个排序算法,待排序数据的有序度不一样,排序的执行时间就会有很大的差别。极端情况下,如果数据已经是有序的,那排序算法不需要做任何操作,执行时间就会非常短。除此之外,如果测试数据规模太小,测试结果可能无法真实地反映算法的性能。比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快!
所以, 我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法。这就是我们今天要讲的时间、空间复杂度分析方法。

大O复杂度表示法
算法的执行效率,粗略地讲,就是算法代码执行的时间。但是,如何在不运行代码的情况下,用“肉眼”得到一段代码的执行时间呢?
这里有段非常简单的代码,求1,2,3…n的累加和。现在,我就带你一块来估算一下这段代码的执行时间。
int cal(int n) {int sum = 0;int i = 1;for (; i <= n; ++i) {sum = sum + i;}return sum;}从CPU的角度来看,这段代码的每一行都执行着类似的操作: 读数据- 运算- 写数据。尽管每行代码对应的CPU执行的个数、执行的时间都不一样,但是,我们这里只是粗略估计,所以可以假设每行代码执行的时间都一样,为unit_time。在这个假设的基础之上,这段代码的总执行时间是多少呢?
第2、3行代码分别需要1个unit_time的执行时间,第4、5行都运行了n遍,所以需要2n*unit_time的执行时间,所以这段代码总的执行时间就是(2n+2)*unit_time。可以看出来, 所有代码的执行时间T(n)与每行代码的执行次数成正比。
按照这个分析思路,我们再来看这段代码。
int cal(int n) {int sum = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1;for (; j <= n; ++j) {sum = sum + i * j;}}}我们依旧假设每个语句的执行时间是unit_time。那这段代码的总执行时间T(n)是多少呢?
第2、3、4行代码,每行都需要1个unit_time的执行时间,第5、6行代码循环执行了n遍,需要2n * unit_time的执行时间,第7、8行代码循环执行了n2遍,所以需要2n2 \* unit_time的执行时间。所以,整段代码总的执行时间T(n) = (2n2+2n+3)*unit_time。
尽管我们不知道unit_time的具体值,但是通过这两段代码执行时间的推导过程,我们可以得到一个非常重要的规律,那就是, 所有代码的执行时间T(n)与每行代码的执行次数f(n)成正比。
我们可以把这个规律总结成一个公式。注意,大O就要登场了!
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9Cs6p0nF-1678772934586)(https://wxwtyproa.oss-cn-hangzhou.aliyuncs.com/22900968aa2b190072c985a08b0e92ef%E3%80%90%E6%B5%B7%E9%87%8F%E8%B5%84%E6%BA%90%EF%BC%9A666java.com%E3%80%91.png)]](https://img-blog.csdnimg.cn/6b71b9984ba9448f81038cc235cfc14a.png)
我来具体解释一下这个公式。其中,T(n)我们已经讲过了,它表示代码执行的时间;n表示数据规模的大小;f(n)表示每行代码执行的次数总和。因为这是一个公式,所以用f(n)来表示。公式中的O,表示代码的执行时间T(n)与f(n)表达式成正比。
所以,第一个例子中的T(n) = O(2n+2),第二个例子中的T(n) = O(2n2+2n+3)。这就是 大O时间复杂度表示法。大O时间复杂度实际上并不具体表示代码真正的执行时间,而是表示 代码执行时间随数据规模增长的变化趋势,所以,也叫作 渐进时间复杂度(asymptotic time complexity),简称 时间复杂度。
当n很大时,你可以把它想象成10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了,如果用大O表示法表示刚讲的那两段代码的时间复杂度,就可以记为:T(n) = O(n); T(n) = O(n2)。
时间复杂度分析
前面介绍了大O时间复杂度的由来和表示方法。现在我们来看下,如何分析一段代码的时间复杂度?我这儿有三个比较实用的方法可以分享给你。

1.只关注循环执行次数最多的一段代码
我刚才说了,大O这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数,只需要记录一个最大阶的量级就可以了。所以, 我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。这段核心代码执行次数的n的量级,就是整段要分析代码的时间复杂度。
为了便于你理解,我还是拿前面的例子来说明。
int cal(int n) {int sum = 0;int i = 1;for (; i <= n; ++i) {sum = sum + i;}return sum;}其中第2、3行代码都是常量级的执行时间,与n的大小无关,所以对于复杂度并没有影响。循环执行次数最多的是第4、5行代码,所以这块代码要重点分析。前面我们也讲过,这两行代码被执行了n次,所以总的时间复杂度就是O(n)。
2.加法法则:总复杂度等于量级最大的那段代码的复杂度
我这里还有一段代码。你可以先试着分析一下,然后再往下看跟我的分析思路是否一样。
int cal(int n) {int sum_1 = 0;int p = 1;for (; p < 100; ++p) {sum_1 = sum_1 + p;}int sum_2 = 0;int q = 1;for (; q < n; ++q) {sum_2 = sum_2 + q;}int sum_3 = 0;int i = 1;int j = 1;for (; i <= n; ++i) {j = 1;for (; j <= n; ++j) {sum_3 = sum_3 + i * j;}}return sum_1 + sum_2 + sum_3;}这个代码分为三部分,分别是求sum_1、sum_2、sum_3。我们可以分别分析每一部分的时间复杂度,然后把它们放到一块儿,再取一个量级最大的作为整段代码的复杂度。
第一段的时间复杂度是多少呢?这段代码循环执行了100次,所以是一个常量的执行时间,跟n的规模无关。
这里我要再强调一下,即便这段代码循环10000次、100000次,只要是一个已知的数,跟n无关,照样也是常量级的执行时间。当n无限大的时候,就可以忽略。尽管对代码的执行时间会有很大影响,但是回到时间复杂度的概念来说,它表示的是一个算法执行效率与数据规模增长的变化趋势,所以不管常量的执行时间多大,我们都可以忽略掉。因为它本身对增长趋势并没有影响。
那第二段代码和第三段代码的时间复杂度是多少呢?答案是O(n)和O(n2),你应该能容易就分析出来。
综合这三段代码的时间复杂度,我们取其中最大的量级。所以,整段代码的时间复杂度就为O(n2)。也就是说: 总的时间复杂度就等于量级最大的那段代码的时间复杂度。那我们将这个规律抽象成公式就是:
如果T1(n)=O(f(n)),T2(n)=O(g(n));那么T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).
3.乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
我刚讲了一个复杂度分析中的加法法则,这儿还有一个 乘法法则。类比一下,你应该能“猜到”公式是什么样子的吧?
如果T1(n)=O(f(n)),T2(n)=O(g(n));那么T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n)).
也就是说,假设T1(n) = O(n),T2(n) = O(n2),则T1(n) * T2(n) = O(n3)。落实到具体的代码上,我们可以把乘法法则看成是 嵌套循环,我举个例子给你解释一下。
int cal(int n) {int ret = 0;int i = 1;for (; i < n; ++i) {ret = ret + f(i);}}int f(int n) {int sum = 0;int i = 1;for (; i < n; ++i) {sum = sum + i;}return sum;}我们单独看cal()函数。假设f()只是一个普通的操作,那第4~6行的时间复杂度就是,T1(n) = O(n)。但f()函数本身不是一个简单的操作,它的时间复杂度是T2(n) = O(n),所以,整个cal()函数的时间复杂度就是,T(n) = T1(n) * T2(n) = O(n*n) = O(n2)。
我刚刚讲了三种复杂度的分析技巧。不过,你并不用刻意去记忆。实际上,复杂度分析这个东西关键在于“熟练”。你只要多看案例,多分析,就能做到“无招胜有招”。
几种常见时间复杂度实例分析
虽然代码千差万别,但是常见的复杂度量级并不多。我稍微总结了一下,这些复杂度量级几乎涵盖了你今后可以接触的所有代码的复杂度量级。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Cbqrgjeu-1678772251826)(https://wxwtyproa.oss-cn-hangzhou.aliyuncs.com/3723793cc5c810e9d5b06bc95325bf0a%E3%80%90%E6%B5%B7%E9%87%8F%E8%B5%84%E6%BA%90%EF%BC%9A666java.com%E3%80%91.jpg)]](https://img-blog.csdnimg.cn/f75ec0b079e74be8ac90043f556374c5.png)
对于刚罗列的复杂度量级,我们可以粗略地分为两类, 多项式量级 和 非多项式量级。其中,非多项式量级只有两个:O(2n)和O(n!)。
我们把时间复杂度为非多项式量级的算法问题叫作NP(Non-Deterministic Polynomial,非确定多项式)问题。
当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。因此,关于NP时间复杂度我就不展开讲了。我们主要来看几种常见的 多项式时间复杂度。
1. O(1)
首先你必须明确一个概念,O(1)只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。比如这段代码,即便有3行,它的时间复杂度也是O(1),而不是O(3)。
int i = 8;int j = 6;int sum = i + j;我稍微总结一下,只要代码的执行时间不随n的增大而增长,这样代码的时间复杂度我们都记作O(1)。或者说, 一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
2. O(logn)、O(nlogn)
对数阶时间复杂度非常常见,同时也是最难分析的一种时间复杂度。我通过一个例子来说明一下。
i=1;while (i <= n) {i = i * 2;}根据我们前面讲的复杂度分析方法,第三行代码是循环执行次数最多的。所以,我们只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。
从代码中可以看出,变量i的值从1开始取,每循环一次就乘以2。当大于n时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量i的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-89Tf6C7n-1678772251826)(https://wxwtyproa.oss-cn-hangzhou.aliyuncs.com/9b1c88264e7a1a20b5954be9bc4bec9a%E3%80%90%E6%B5%B7%E9%87%8F%E8%B5%84%E6%BA%90%EF%BC%9A666java.com%E3%80%91.jpg)]](https://img-blog.csdnimg.cn/922fdfbe86a04d61ab9685529dd7936e.png)
所以,我们只要知道x值是多少,就知道这行代码执行的次数了。通过2x=n求解x这个问题我们想高中应该就学过了,我就不多说了。x=log2n,所以,这段代码的时间复杂度就是O(log2n)。
现在,我把代码稍微改下,你再看看,这段代码的时间复杂度是多少?
i=1;while (i <= n) {i = i * 3;}根据我刚刚讲的思路,很简单就能看出来,这段代码的时间复杂度为O(log3n)。
实际上,不管是以2为底、以3为底,还是以10为底,我们可以把所有对数阶的时间复杂度都记为O(logn)。为什么呢?
我们知道,对数之间是可以互相转换的,log3n就等于log32 * log2n,所以O(log3n) = O(C * log2n),其中C=log32是一个常量。基于我们前面的一个理论: 在采用大O标记复杂度的时候,可以忽略系数,即O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于O(log3n)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为O(logn)。
如果你理解了我前面讲的O(logn),那O(nlogn)就很容易理解了。还记得我们刚讲的乘法法则吗?如果一段代码的时间复杂度是O(logn),我们循环执行n遍,时间复杂度就是O(nlogn)了。而且,O(nlogn)也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序的时间复杂度都是O(nlogn)。
3. O(m+n)、O(m*n)
我们再来讲一种跟前面都不一样的时间复杂度,代码的复杂度 由两个数据的规模 来决定。老规矩,先看代码!
int cal(int m, int n) {int sum_1 = 0;int i = 1;for (; i < m; ++i) {sum_1 = sum_1 + i;}int sum_2 = 0;int j = 1;for (; j < n; ++j) {sum_2 = sum_2 + j;}return sum_1 + sum_2;
}从代码中可以看出,m和n是表示两个数据规模。我们无法事先评估m和n谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))。

空间复杂度分析
前面,咱们花了很长时间讲大O表示法和时间复杂度分析,理解了前面讲的内容,空间复杂度分析方法学起来就非常简单了。
前面我讲过,时间复杂度的全称是 渐进时间复杂度, 表示算法的执行时间与数据规模之间的增长关系。类比一下,空间复杂度全称就是 渐进空间复杂度(asymptotic space complexity), 表示算法的存储空间与数据规模之间的增长关系。
我还是拿具体的例子来给你说明。(这段代码有点“傻”,一般没人会这么写,我这么写只是为了方便给你解释。)
void print(int n) {int i = 0;int[] a = new int[n];for (i; i <n; ++i) {a[i] = i * i;}for (i = n-1; i >= 0; --i) {print out a[i]}
}跟时间复杂度分析一样,我们可以看到,第2行代码中,我们申请了一个空间存储变量i,但是它是常量阶的,跟数据规模n没有关系,所以我们可以忽略。第3行申请了一个大小为n的int类型数组,除此之外,剩下的代码都没有占用更多的空间,所以整段代码的空间复杂度就是O(n)。
我们常见的空间复杂度就是O(1)、O(n)、O(n2 ),像O(logn)、O(nlogn)这样的对数阶复杂度平时都用不到。而且,空间复杂度分析比时间复杂度分析要简单很多。所以,对于空间复杂度,掌握刚我说的这些内容已经足够了。
内容小结
基础复杂度分析的知识到此就讲完了,我们来总结一下。
复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系,可以粗略地表示,越高阶复杂度的算法,执行效率越低。常见的复杂度并不多,从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。你就会发现几乎所有的数据结构和算法的复杂度都跑不出这几个。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1FnkRS4A-1678772251826)(https://wxwtyproa.oss-cn-hangzhou.aliyuncs.com/497a3f120b7debee07dc0d03984faf04%E3%80%90%E6%B5%B7%E9%87%8F%E8%B5%84%E6%BA%90%EF%BC%9A666java.com%E3%80%91.jpg)]](https://img-blog.csdnimg.cn/28531c965df04dd19b47904f163f789f.png)
最后说一句
感谢大家的阅读,文章通过网络资源与自己的学习过程整理出来,希望能帮助到大家。
才疏学浅,难免会有纰漏,如果你发现了错误的地方,可以提出来,我会对其加以修改。

相关文章:

【拳打蓝桥杯】算法前置课——时间复杂度与空间复杂度
文章目录前言为什么需要复杂度分析?大O复杂度表示法时间复杂度分析几种常见时间复杂度实例分析空间复杂度分析内容小结最后说一句🐱🐉作者简介:大家好,我是黑洞晓威,一名大二学生,希望和大家一…...

vite中动态引入图片,打包之后找不到图片地址?
一般来说项目中我们集中存放图片,然后希望在页面中直接引入! 更好的就是直接在模板中调用一个函数 然后传入图片的名字就可以显示出来 事实上确实可以办到,我们用到了一个 new URL import.meta.url这俩个东西 再src目录下 static 下创建一…...

Docker 常用命令大全
目录 一、Docker (一)Docker基础命令 (二)docker镜像命令 (三)docker容器命令 (四)docker运维命令 一、Docker 容器是一种虚拟化技术,容器是镜像实例…...

React项目规范:目录结构、根目录别名、CSS重置、路由、redux、二次封装axios
React项目(一)一、创建项目二、目录结构三、craco配置别名并安装less1.craco安装2.配置别名3.安装less四、CSS样式重置五、配置路由六、配置Redux1.创建大仓库2.创建小仓库(1)方式1:RTK(2)方式2…...

SystemVerilog 教程第一章:简介
SystemVerilog 教程像 Verilog 和 VHDL 之类的硬件描述语言 (HDL) 主要用于描述硬件行为,以便将其转换为由组合门电路和时序元件组成的数字块。为了验证 HDL 中的硬件描述正确无误,就需要具有更多功能特性的面向对象的编程语言 (OOP) 来支持复杂的测试过…...

【Java|基础篇】逻辑控制-顺序结构、分支结构和循环结构
文章目录顺序结构分支结构if单分支语句if else双分支语句if else if else多分支语句switch语句循环语句for循环while循环do while循环continuebreak总结顺序结构 顺序结构是指代码按照从上往下的顺序依次执行 分支结构 选择语句是条件成立时,才会执行的语句.共有三种.分为是if…...

【数据挖掘实战】——家用电器用户行为分析及事件识别(BP神经网络)
项目地址:Datamining_project: 数据挖掘实战项目代码 目录 一、背景和挖掘目标 1、问题背景 2、原始数据 3、挖掘目标 二、分析方法与过程 1、初步分析 2、总体流程 第一步:数据抽取 第二步:探索分析 第三步:数据的预处…...

Kmeans聚类算法-python
import random import pandas as pd import numpy as np import matplotlib.pyplot as plt # 计算欧拉距离 def calcDis(dataSet, centroids, k): clalist[] for data in dataSet: diff np.tile(data, (k, 1)) - centroids #相减 (np.tile(a,(2,1))就是把…...

Linux|奇怪的知识|locate命令---文件管理小工具
前言: Linux的命令是非常多的,有一些冷门的命令,虽然很少用,但可能会有意想不到的功能,例如,本文将要介绍的locate命令。 (平常很少会想到使用此命令,find命令使用的更多,偶然想起…...

Cadence Allegro 导出Function Pin Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Function Pin Reportt作用3,Function Pin Report示例4,Function Pin Report导出方法4.1,方法14.2,方法2B站关注“硬小二”浏览更多演示视频 1,概述...

蓝桥杯2018年第九题-缩位求和
题目:在电子计算机普及以前,人们经常用一个粗略的方法来验算四则运算是否正确。比如:248 * 15 3720把乘数和被乘数分别逐位求和,如果是多位数再逐位求和,直到是1位数,得2 4 8 14 > 1 4 5;1 5 65…...

基于Yolv5s的口罩检测
1.Yolov5算法原理和网络结构 YOLOv5按照网络深度和网络宽度的大小,可以分为YO-LOv5s、YOLOv5m、YOLOv5l、YOLOv5x。本文使用YOLOv5s,它的网络结构最为小巧,同时图像推理速度最快达0.007s。YO-LOv5的网络结构主要由四部分组成,分别…...

Linux基本命令
Linux基本命令Linux的目录结构Linux命令入门目录切换相关命令(cd/pwd)相对路径、绝对路径和特殊路径符创建目录命令(mkdir)文件操作命令part1 (touch、cat、more)文件操作命令part2 (cp、mv、rm)查找命令 (which、find…...

云原生场景下的安全左移
本博客地址:https://security.blog.csdn.net/article/details/129430859 一、安全左移概述 安全左移需要考虑开发安全、软件供应链安全、镜像仓库、配置核查这四个部分。 首先是开发安全,安全团队需要关注代码漏洞,比如使用代码检查工具进…...

mysql面试经典问题
文章目录 1. 能说下myisam 和 innodb的区别吗?2. 说下mysql的索引有哪些吧,聚簇和非聚簇索引又是什么?3. 那你知道什么是覆盖索引和回表吗?4. 锁的类型有哪些呢5. 你能说下事务的基本特性和隔离级别吗?6. 那ACID靠什么保证的呢?7. 那你说说什么是幻读,什么是MVCC?幻读什…...
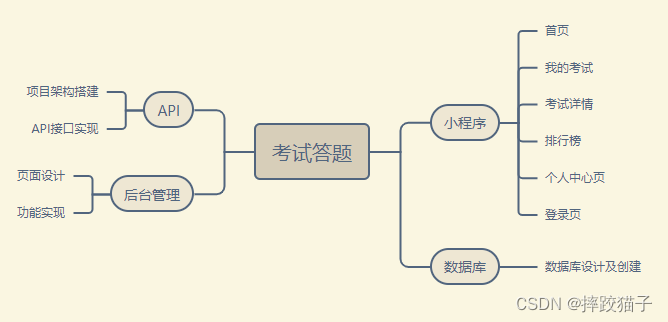
微信小程序|基于小程序+C#制作一个考试答题小程序
基于小程序+C#制作一个考试答题小程序打破传统线下考试答题的边界线问题,使考试不用再局限与某个统一的场所,只要有设备,哪里都能考试。 一、小程序...

【1605. 给定行和列的和求可行矩阵】
来源:力扣(LeetCode) 描述: 给你两个非负整数数组 rowSum 和 colSum ,其中 rowSum[i] 是二维矩阵中第 i 行元素的和, colSum[j] 是第 j 列元素的和。换言之你不知道矩阵里的每个元素,但是你知…...
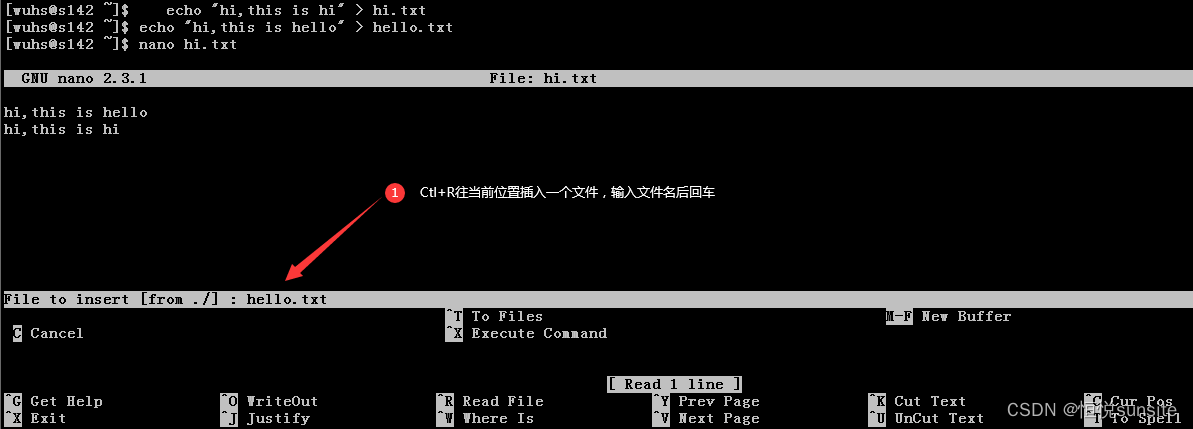
Linux命令之nano命令
一、nano命令简介 nano是一个小型、免费、友好的编辑器,旨在取代非免费Pine包中的默认编辑器Pico。nano不仅复制了Pico的外观,还实现了Pico中一些缺失(或默认禁用)的功能,例如“搜索和替换”和“转到行号和列号”。nan…...
)
IT项目管理(作业1)
一.单选题(共12题,100.0分) 1.以下哪项是项目的一个实例?( ) A、改进现有的业务流程或程序B、为公司运营提供信息技术支持C、批量生产一种新近开发出来的家用电冰箱D、管理一个公司 我的答案:A 2.下列哪项不能成为项目结束的理由?( ) A…...

蓝桥杯嵌入式(G4系列):串口收发
前言: 在整个蓝桥杯考试中涉及串口的次数还是较多,这里写下这篇博客,记录一下自己的学习过程。 STM32Cubemx配置: 首先,我们点击左侧的Connectivity选择USART1进行如下配置。 使能串口中断 在左侧的管脚配置上也要做出…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
