第十三届蓝桥杯A组:选数异或——三种解法(线段树、DP、ST表)
[蓝桥杯 2022 省 A] 选数异或
题目描述
给定一个长度为 nnn 的数列 A1,A2,⋯,AnA_{1}, A_{2}, \cdots, A_{n}A1,A2,⋯,An 和一个非负整数 xxx, 给定 mmm 次查询, 每次询问能否从某个区间 [l,r][l, r][l,r] 中选择两个数使得他们的异或等于 xxx 。
输入格式
输入的第一行包含三个整数 n,m,xn, m, xn,m,x 。
第二行包含 nnn 个整数 A1,A2,⋯,AnA_{1}, A_{2}, \cdots, A_{n}A1,A2,⋯,An。
接下来 mmm 行,每行包含两个整数 li,ril_{i}, r_{i}li,ri 表示询问区间 [li,ri]\left[l_{i}, r_{i}\right][li,ri] 。
输出格式
对于每个询问, 如果该区间内存在两个数的异或为 xxx 则输出 yes, 否则输出 no。
样例 #1
样例输入 #1
4 4 1
1 2 3 4
1 4
1 2
2 3
3 3
样例输出 #1
yes
no
yes
no
提示
【样例说明】
显然整个数列中只有 2,3 的异或为 1 。
【评测用例规模与约定】
对于 20%20 \%20% 的评测用例, 1≤n,m≤1001 \leq n, m \leq 1001≤n,m≤100;
对于 40%40 \%40% 的评测用例, 1≤n,m≤10001 \leq n, m \leq 10001≤n,m≤1000;
对于所有评测用例, 1≤n,m≤105,0≤x<220,1≤li≤ri≤n1 \leq n, m \leq 10^5,0 \leq x<2^{20}, 1 \leq l_{i} \leq r_{i} \leq n1≤n,m≤105,0≤x<220,1≤li≤ri≤n , 0≤Ai<2200 \leq A_{i}<2^{20}0≤Ai<220 。
蓝桥杯 2022 省赛 A 组 D 题。
分析
A组的题,题目有三种解法,但是这道题无论啥解法,实际上是万变不离其宗的,就是他的关键的对于某个点的预处理。想要解这题主要还是要想出这个处理。之所以写不同的这三种解法,主要是复习一下模板吧
首先,我们容易知道:若a^b=x,那么a^x=b,对于数组a[i],我们可以通过关系式,找到a[i]^x的左边的最靠近下标,明显我们需要找到最靠近的下标,而当这个下标是大于等于所需要找的区间的左端点,即可满足这个区间内可以找到两个数的异或为x。
当对于一个数,其左边没有数与其异或等于x时,那么就将其置为0,而当我们不断输入数字的时候,我们需要同时存储这个数的下标,方便循环到下一个下标的时候找到这个数字(通过a^x=b这样的关系),具体看代码
解法一:线段树
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int t[400005],a[100005],Left[100005],pos[2000005];
inline void buildtree(int k,int l,int r){if(l==r){t[k]=Left[r];return;}int mid=(l+r)>>1;buildtree(k<<1,l,mid),buildtree(k<<1|1,mid+1,r);t[k]=max(t[k<<1],t[k<<1|1]);
}
inline int query(int k,int l,int r,int x,int y){if(l==x&&r==y)return t[k];int mid=(l+r)>>1;if(y<=mid)return query(k<<1,l,mid,x,y);elseif(x>mid)return query(k<<1|1,mid+1,r,x,y);else return max(query(k<<1,l,mid,x,mid),query(k<<1|1,mid+1,r,mid+1,y));
}
int main(){int n,m,x;cin>>n>>m>>x;for(int i=1;i<=n;++i){scanf("%d",&a[i]);Left[i]=pos[a[i]^x];pos[a[i]]=i;}buildtree(1,1,n);while(m--){int x,y;scanf("%d%d",&x,&y);int k=query(1,1,n,x,y);if(k>=x)printf("yes\n");else printf("no\n");}
}
解法二:DP
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int f[100005],pos[5000005];
int main(){int n,m,x;cin>>n>>m>>x;for(int i=1;i<=n;++i){int a;scanf("%d",&a);f[i]=max(f[i-1],pos[a^x]);pos[a]=i;}while(m--){int l,r;scanf("%d%d",&l,&r);if(f[r]>=l)printf("yes\n");else printf("no\n");}
}
解法三:ST表
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int st[100005][20],pos[5000005];
int main(){int n,m,x;cin>>n>>m>>x;for(int i=1;i<=n;++i){int a;scanf("%d",&a);st[i][0]=pos[a^x];pos[a]=i;}int k=log2(n);for(int i=1;i<=k;++i)for(int j=1;j+(1<<i)-1<=n;++j)st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);while(m--){int l,r;scanf("%d%d",&l,&r);int len=log2(r-l+1);int p=max(st[l][len],st[r-(1<<len)+1][len]);if(p>=l)printf("yes\n");else printf("no\n");}
}
相关文章:
)
第十三届蓝桥杯A组:选数异或——三种解法(线段树、DP、ST表)
[蓝桥杯 2022 省 A] 选数异或 题目描述 给定一个长度为 nnn 的数列 A1,A2,⋯,AnA_{1}, A_{2}, \cdots, A_{n}A1,A2,⋯,An 和一个非负整数 xxx, 给定 mmm 次查询, 每次询问能否从某个区间 [l,r][l, r][l,r] 中选择两个数使得他们的异或等于 xxx 。 输入格式 输入的第一…...

【CTF】CTF竞赛介绍以及刷题网址
CTF(Capture The Flag)中文一般译作夺旗赛,在网络安全领域中指的是网络安全技术人员之间进行技术竞技的一种比赛形式。CTF起源于1996年DEFCON全球黑客大会,以代替之前黑客们通过互相发起真实攻击进行技术比拼的方式。发展至今&…...
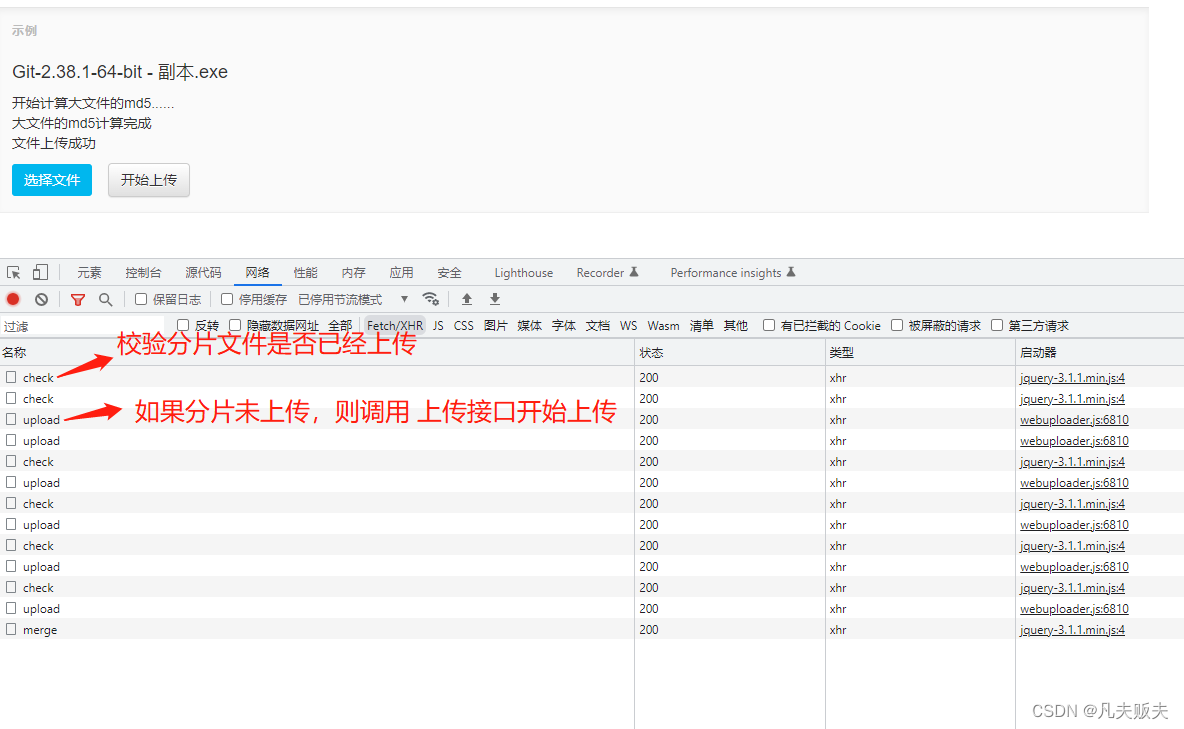
Springboot怎么优雅实现大文件的上传
前言在软件工程里,在处理“大”的时候一直是一个难点和难点,如并发大、数据量大、文件大,对硬件进行升级可以解决一些问题,但这并不最聪明的办法,而对于老板来说,这也不是成本最小的办法。作为开发人员来说…...
2月编程语言排行榜新鲜出炉,谁又摘得桂冠?
近日,TIOBE公布了2023年2月编程语言排行榜,本月各个语言表现如何?谁又摘得桂冠?一起来看看吧! TIOBE 2月Top15编程语言: 详细榜单查看TIOBE官网 https://www.tiobe.com/tiobe-index/ 关注IT行业的小伙伴…...
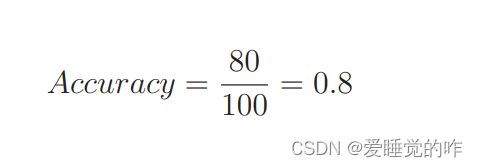
机器学习中的数学原理——模型评估与交叉验证
惭愧惭愧!机器学习中的数学原理这个专栏已经很久没有更新了!前段时间一直在学习深度学习,paddlepaddle,刷题专栏跟新了,这个专栏就被打入冷宫了。这个专栏名为白话机器学习中数学学习笔记,主要是用来分享一…...
JAVA开发(JSP的9大内置对象和4大作用域)
背景: 在springboot横行的javaweb开发中,现在的后端开发工程师基本不需要写前端JSP页面。但是作为web开发工程师,不懂JSP的原理和作用,几乎是不行的。 JSP技术介绍: JSP(全称Java Server Pagesÿ…...
EKF失控保护)
(4)EKF失控保护
文章目录 前言 4.1 什么时候会触发? 4.2 当失控保护触发时,会发生什么?...
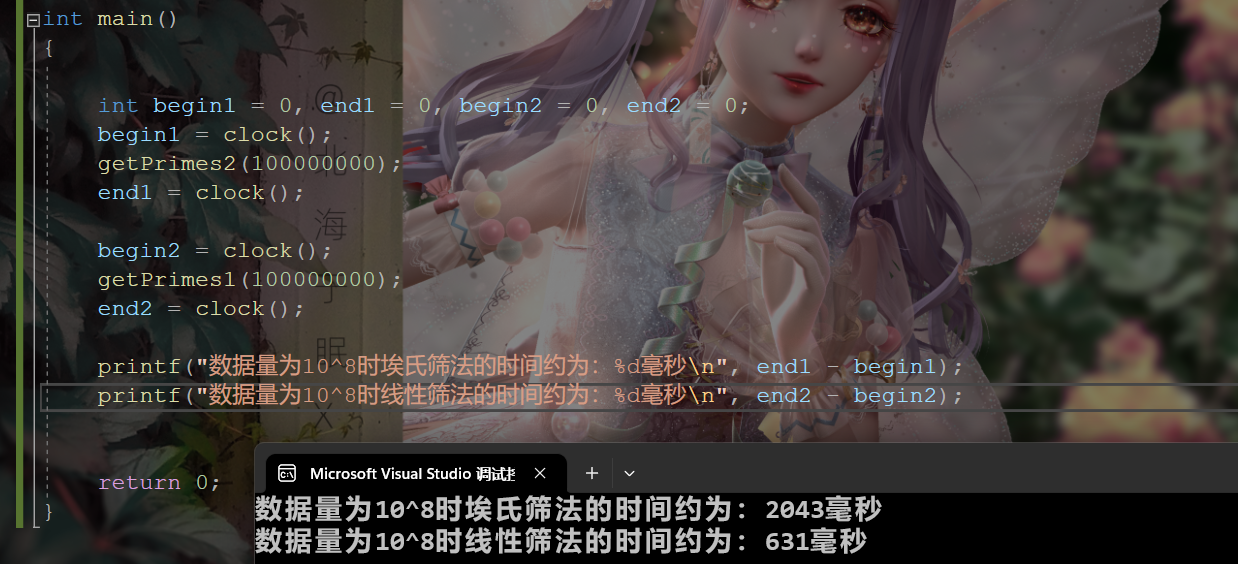
数论----质数的求解(C/C++)
CSDN的uu,你们好呀,今天我们要学习的内容是数论哦!这也是算法题中的一类题目吧。记好安全带,准备发车咯!🚀学习数论的意义📢算法导论说:“数论曾经被视为一种虽然优美但却没什么用处…...
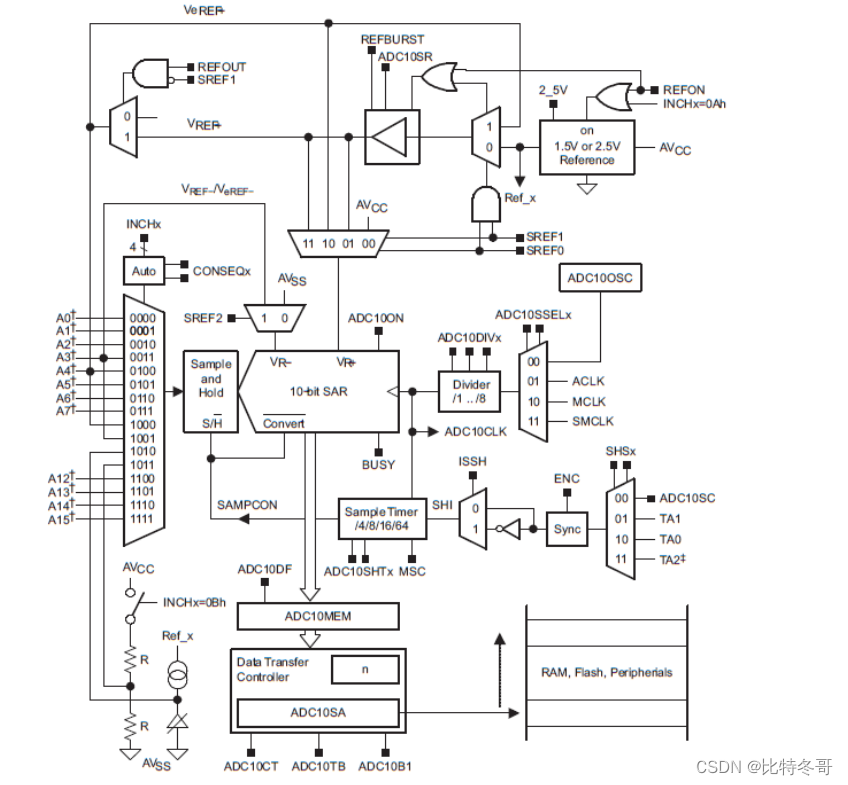
【电赛MSP430系列】GPIO、LED、按键、时钟、中断、串口、定时器、PWM、ADC
文章目录MSP430一、GPIO二、点亮LED三、按键控制LED四、更改主时钟五、串口通信六、串口中断七、外部中断八、定时器九、定时器中断十、PWM十一、ADCMSP430 MSP430 是德州仪器(TI)一款性能卓越的超低功耗 16 位单片机,自问世以来,…...

【Linux】进程理解与学习(Ⅱ)
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹相关文章推荐:【Linux】冯.诺依曼体系结构与操作系统【Linux】进程理解与学习(Ⅰ)浅谈Linux下的shell--BASH前言章节…...

vscode 爽到起飞的快捷键
这里写目录标题1. 窗口操作2. 代码编辑3. 批量操作4. 错误处理1. 窗口操作 文件之间切换: CtrlTab 切出一个新的编辑器窗口(最多3个): Ctrl\ 切换左中右3个编辑器窗口的快捷键: Ctrl1 Ctrl2 Ctrl3 2. 代码编辑 代码格式化: ShiftAltF 向上或向下移动一行: Alt…...
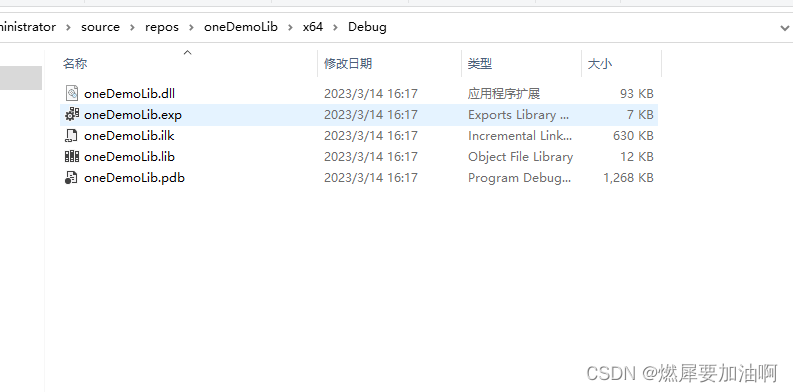
vs +qt 打包.cpp和.h为DLL文件
文章目录一 编译成库1 创建一个Qt library 项目2,将已有的文件拷贝到项目目录下3 在项目中添加现有项4,拷贝头文件到需要暴露给外面使用的类的头文件中5 拷贝xxx_EXPORT的宏到需要被暴露的类的名前面6 然后点击编译 就完成了。得到的dll文件在debug里面二…...

echarts有滑块
vue下使用echarts折线图及其横坐标拖拽功能 drawLine() {let that this,lineDate [],dispatchCount [],finishCount [],newCount [];let param {// 参数};axios.post(url, param).then(function(response) {let rs response.data.data;if (rs ! undefined && rs…...

MATLAB绘制ROC曲线
ROC曲线(Receiver Operating Characteristic Curve) 1 简介 ROC曲线是用于评估二元分类模型(如Logistic回归)表现优劣的一种工具,其横轴表示假阳性率(false positive rate,FPR),即实际为负例但…...
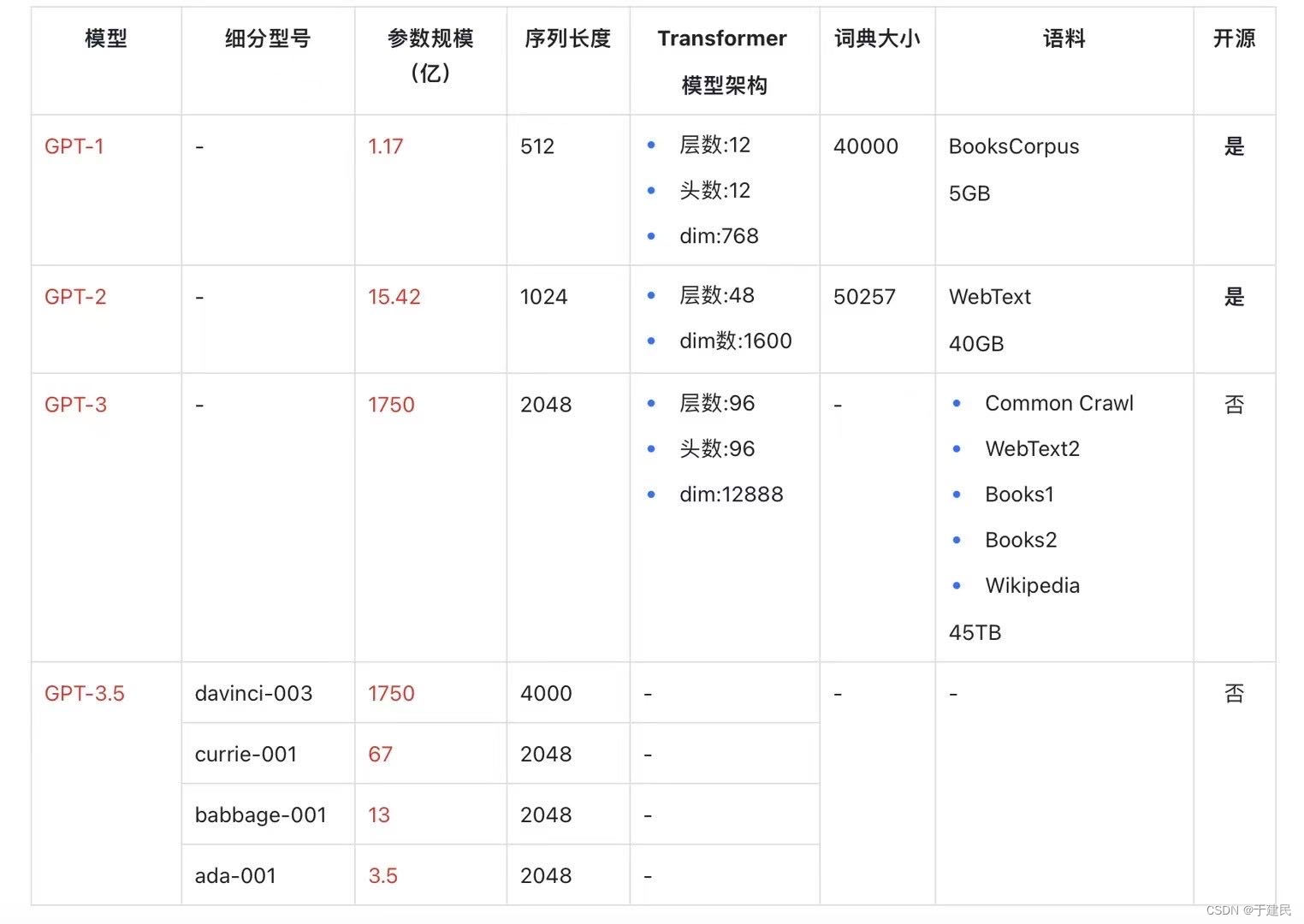
ChatGPT前传
文章目录前言GPT概述GPT-1代GPT-1 学习目标和概念介绍GPT-1 训练数据集GPT-1 模型结构和应用细节GPT-1 效果性能和总结GPT-2代GPT-2 学习目标和概念介绍GPT-2 训练数据集GPT-2 模型结构和应用细节GPT-2 性能效果和总结GPT-3代GPT-3 学习目标和概念介绍GPT-3 训练数据集GPT-3 模…...

我的十年编程路 2020年篇
我出生在1990年,2020年到来的时候,我完成了一项成就:奔三。同时,也开启了新的征程:奔四。 2020年的春节是在广州的丈母娘家度过的,春节后大概是初五,或者是初六,我和媳妇就返回天津…...

力扣-SQL【入门】
https://leetcode.cn/study-plan/sql/?progressxhqm4sjh 目录选择595. 大的国家1757. 可回收且低脂的产品584. 寻找用户推荐人183. 从不订购的客户排序 & 修改1873. 计算特殊奖金627. 变更性别196. 删除重复的电子邮箱选择 595. 大的国家 # Write your MySQL query state…...
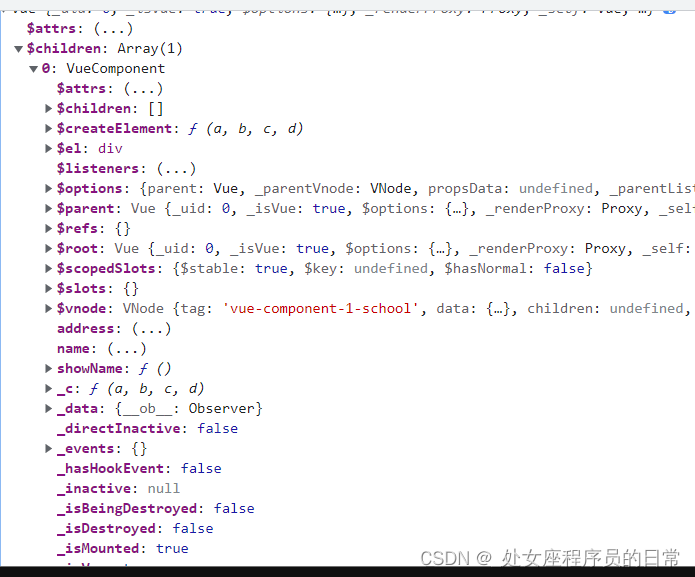
Vue中组件到底是什么
1.先说结论: Vue中组件本质是一个名为VueComponent的构造函数,且不是程序员定义的,是Vue.extend生成的。 2.我们使用组件时发生了什么? 比如定义了一个school,然后在页面上使用它 我们只需要写 < school/ > 或< school &…...

不同时间间隔数据对统计结果的影响
目录摘要1. 实测数据来源2. 数据分析方法3 结果分析3.1 波况分析摘要 采用不同的波浪观测方法所获得的波浪数据的时间间隔不一致,其数据的准确性须进行分析。基于大埕湾逐时周年波浪观测数据,截取不同时间间隔的波浪数据,采用统计和相关分析…...

hudi系列-数据写入方式及使用场景
hudi支持多种数据写入方式:insert、bulk_insert、upsert、boostrap,我们可以根据数据本身属性(append-only或upsert)来选择insert和upsert方式,同时也支持对历史数据的高效同步并嫁接到实时流程。 这里的使用技术组合为flink + hudi-0.11 upsert 这是hudi默认的写入方式,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
