二叉树的序列化和反序列化(Java)
概述
关于面试中常见的其他二叉树算法题,参考面试+算法之二叉树(Java)。二叉树的定义(注意到有使用lombok提供的两个注解):
@lombok.Data
@lombok.AllArgsConstructor
private static class TreeNode {private TreeNode left;private TreeNode right;private final int val;TreeNode(int x) {this.val = x;}
}
将有序数组转换为二叉搜索树
给定一个升序排序的整数数组nums,将其转换为一棵高度平衡的二叉搜索树。来自LeetCode
分析:给定一个有序数组,转换成二叉搜索树,即左子树小于根节点,根节点小于右子树,满足条件的二叉搜索树显然不止一种。
一般情况下,大多数人都会考虑取数组的中间元素作为根节点。为啥选择中间元素,为了确保得到的二叉树的高度差尽可能小。如果数组的元素个数是奇数,根节点可以唯一确定;如果是偶数,则根节点不唯一。所以,
如果题目没有限定高度平衡的二叉树,则得到的二叉树将会更多。最差的情况就是退化成仅有根节点和左子树或右子树的二叉树,即退化成类似链表的结构。
采用递归的方法:
public static TreeNode sortedArrayToBST(int[] nums) {return traversal(nums, 0, nums.length - 1);
}private static TreeNode traversal(int[] nums, int left, int right) {if (left > right) {// 叶子节点return null;}int mid = left + ((right - left) / 2);TreeNode node = new TreeNode(nums[mid]);node.left = traversal(nums, left, mid - 1);node.right = traversal(nums, mid + 1, right);return node;
}
从中序与后序遍历序列构造二叉树
来自LeetCode
public static TreeNode buildTree(int[] inOrder, int[] postOrder) {return helper(inOrder, postOrder, postOrder.length - 1, 0, inOrder.length - 1);
}private static TreeNode helper(int[] inOrder, int[] postOrder, int postEnd, int inStart, int inEnd) {if (inStart > inEnd) {return null;}int currentVal = postOrder[postEnd];TreeNode current = new TreeNode(currentVal);int inIndex = 0;for (int i = inStart; i <= inEnd; i++) {if (inOrder[i] == currentVal) {inIndex = i;}}TreeNode left = helper(inOrder, postOrder, postEnd - (inEnd - inIndex) - 1, inStart, inIndex - 1);TreeNode right = helper(inOrder, postOrder, postEnd - 1, inIndex + 1, inEnd);current.left = left;current.right = right;return current;
}
序列化
递归的思想,采用前序遍历,对空节点需要特殊处理,使用任何占位符都可:
public static String serialize(TreeNode root) {StringBuilder sb = new StringBuilder();serializeHelper(root, sb);return sb.substring(0, sb.length() - 1);
}private static void serializeHelper(TreeNode node, StringBuilder sb) {if (node == null) {sb.append("#,"); // 空节点return;}sb.append(node.val).append(",");serializeHelper(node.left, sb);serializeHelper(node.right, sb);
}
反序列化
能否从序列化后的字符串,反序列化得到一棵树呢?
答案是可以的。前提是知道对空节点的处理(填位字符串)策略,节点的间隔(字符)策略。
能否从序列化后的字符串,反序列化得到原始的二叉树?
答案是不一定,如果想要反序列化得到原始的二叉树,有一些前提条件:
- 序列化方案,是前序、中序还是后序
- 对空节点的处理策略
- 节点的间隔(字符)策略
public static TreeNode deserialize(String data) {LinkedList<String> nodes = new LinkedList<>(Arrays.asList(data.split(",")));return deserializeHelper(nodes);
}private static TreeNode deserializeHelper(LinkedList<String> nodes) {String val = nodes.removeFirst();if (val.equals("#")) {return null;}TreeNode node = new TreeNode(Integer.parseInt(val));node.left = deserializeHelper(nodes);node.right = deserializeHelper(nodes);return node;
}
测试方法:
public static void main(String[] args) {TreeNode head = init();String s = serialize(head);// TreeNode.toString()方法String b = deserialize(s).toString();System.out.println("序列化:" + s);System.out.println("反序列化:" + b);
}
附TreeNode.toString()方法:
@Override
public String toString() {return toString(this);
}public String toString(TreeNode r) {if (r == null) {return "#";} else {return r.val + "," + toString(r.left) + "," + toString(r.right);}
}
输出:
序列化:8,4,2,#,1,#,#,3,#,#,7,#,6,5,#,#,#
反序列化:8,4,2,#,1,#,#,3,#,#,7,#,6,5,#,#,#
结论:
- 已知序列化方案和空节点处理策略后,可唯一反序列化得到原始二叉树
- 二叉树的打印方法里对空节点的处理策略保持一致,且间隔符都是
,,则两个字符串相等
进阶
如果不知道序列化方案,如何反序列化得到二叉树?
结论:可以反序列化,但是不一定是原始的二叉树,所以这个反序列化也没有任何意义。
为了解决这个问题,有几个选择:
- 使用包含遍历顺序信息的序列化格式:
在序列化字符串中包含遍历顺序信息。例如,在字符串前面加上遍历顺序的标识符(如P表示前序(Pre-order),I表示中序(In-order),O表示后序(post-Order))。 - 双序列化:
使用两种不同的遍历顺序分别序列化树,并将两个序列化结果一起保存。两种方案字符|以分隔。例如,使用前序和中序,或后序和中序。
其中方案二基于这样一个已被证实的结论:若存在对同一棵二叉树的两种不一样的遍历(序列化)方案,则一定可以唯一确定这棵二叉树。
/*** 序列化二叉树(前序和中序)*/
public static String serialize1(TreeNode root) {StringBuilder preOrder = new StringBuilder();StringBuilder inOrder = new StringBuilder();serializePreOrder(root, preOrder);serializeInOrder(root, inOrder);return preOrder.toString() + "|" + inOrder.toString(); // 使用 | 作为分隔符
}private static void serializePreOrder(TreeNode node, StringBuilder sb) {if (node == null) {sb.append("#,");return;}sb.append(node.val).append(",");serializePreOrder(node.left, sb);serializePreOrder(node.right, sb);
}private static void serializeInOrder(TreeNode node, StringBuilder sb) {if (node == null) {sb.append("#,");return;}serializeInOrder(node.left, sb);sb.append(node.val).append(",");serializeInOrder(node.right, sb);
}/*** 反序列化二叉树*/
public static TreeNode deserialize1(String data) {// 需预知的信息:两个字符串的分隔符String[] parts = data.split("\\|");// 需预知的信息:序列化的间隔符LinkedList<String> preOrderNodes = new LinkedList<>(Arrays.asList(parts[0].split(",")));LinkedList<String> inOrderNodes = new LinkedList<>(Arrays.asList(parts[1].split(",")));return buildTree(preOrderNodes, inOrderNodes);
}private static TreeNode buildTree(LinkedList<String> preOrderNodes, LinkedList<String> inOrderNodes) {// 需预知的信息:对空节点的处理策略if (preOrderNodes.isEmpty() || preOrderNodes.peek().equals("#")) {preOrderNodes.poll();inOrderNodes.poll();return null;}String rootVal = preOrderNodes.poll();TreeNode root = new TreeNode(Integer.parseInt(rootVal));int inOrderIndex = inOrderNodes.indexOf(rootVal);root.left = buildTree(preOrderNodes, new LinkedList<>(inOrderNodes.subList(0, inOrderIndex)));root.right = buildTree(preOrderNodes, new LinkedList<>(inOrderNodes.subList(inOrderIndex + 1, inOrderNodes.size())));inOrderNodes.poll();return root;
}
可以看出,这两个方案还是得提前知道一些规则信息。事实上,网络通信就是一个包含序列化和反序列化的过程,如果不知道序列化规则(即协议信息),则反序列化几乎没有意义。
参考
相关文章:
)
二叉树的序列化和反序列化(Java)
概述 关于面试中常见的其他二叉树算法题,参考面试算法之二叉树(Java)。二叉树的定义(注意到有使用lombok提供的两个注解): lombok.Data lombok.AllArgsConstructor private static class TreeNode {private TreeNode left;priva…...

Java中的泛型类
Java中的泛类 Java 的泛型(Generics)是一种语言特性,允许你定义类、接口和方法时使用类型参数。这使得代码更具可读性和安全性,因为编译器能够在编译时检查类型,而不是在运行时。 泛型类 定义泛型类时,可…...

57、Flink 的项目配置概述
1)概览 1.开始 要开始使用 Flink 应用程序,请使用以下命令、脚本和模板来创建 Flink 项目。 可以使用如下的 Maven 命令或快速启动脚本,基于原型创建一个项目。 a)Maven 命令 mvn archetype:generate \-Darch…...

零基础自学爬虫技术该从哪里入手?
零基础学习Python并不一定是困难的,这主要取决于个人的学习方法、投入的时间以及学习目标的设定。Python是一门相对容易入门的编程语言,它有着简洁的语法、丰富的库和广泛的应用领域(如数据分析、Web开发、人工智能等),…...

Vue.js 基础入门指南
前言 在前端开发的广阔领域中,Vue.js 无疑是一颗璀璨的明星,以其渐进式框架的特性吸引了无数开发者的目光。Vue.js 旨在通过简洁的 API 实现响应式的数据绑定和组合的视图组件,使得构建用户界面变得既快速又简单。本文将带你走进 Vue.js 的世…...

山泰科技集团陈玉东:争当数字化时代的知识产权卫士
随着互联网和数字技术的飞速普及,大版权时代已经悄然到来。在这个新时代,信息的传播速度、广度和深度均达到了前所未有的高度,极大地拓展了人们的精神世界和知识视野。然而,这一科技发展的浪潮也为版权保护带来了前所未有的挑战。…...
WBCE CMS v1.5.2 远程命令执行漏洞(CVE-2022-25099)
前言 CVE-2022-25099 是一个影响 WBCE CMS v1.5.2 的严重安全漏洞,具体存在于 /languages/index.php 组件中。该漏洞允许攻击者通过上传精心构造的 PHP 文件在受影响的系统上执行任意代码。 技术细节 受影响组件:/languages/index.php受影响版本&…...

鸿蒙语言基础类库:【@ohos.url (URL字符串解析)】
URL字符串解析 说明: 本模块首批接口从API version 7开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 导入…...

【AutoencoderKL】基于stable-diffusion-v1.4的vae对图像重构
模型地址:https://huggingface.co/CompVis/stable-diffusion-v1-4/tree/main/vae 主要参考:Using-Stable-Diffusion-VAE-to-encode-satellite-images sd1.4 vae 下载到本地 from diffusers import AutoencoderKL from PIL import Image import torch import to…...
)
《警世贤文》摘抄:守法篇、惜时篇、修性篇、修身篇、待人篇、防人篇(建议多读书、多看报、少吃零食多睡觉)
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140243440 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
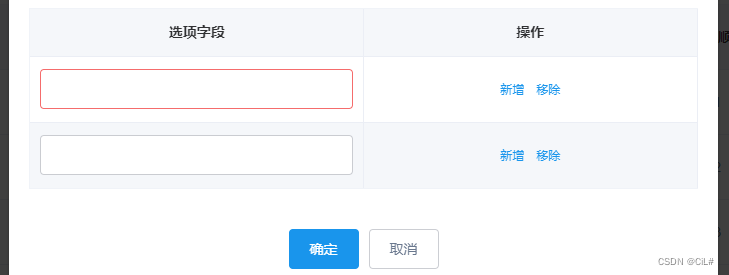
vue2+element-ui新增编辑表格+删除行
实现效果: 代码实现 : <el-table :data"dataForm.updateData"border:header-cell-style"{text-align:center}":cell-style"{text-align:center}"><el-table-column label"选项字段"align"center&…...

Day05-组织架构-角色管理
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1.组织架构-编辑部门-弹出层获取数据2.组织架构-编辑部门-编辑表单校验3.组织架构-编辑部门-确认取消4.组织架构-删除部门5.角色管理-搭建页面结构6.角色管理-获取数…...

【LLM】二、python调用本地的ollama部署的大模型
系列文章目录 往期文章: 【LLM】一、利用ollama本地部署大模型 目录 文章目录 前言 一、ollama库调用 二、langchain调用 三、requests调用 四、相关参数说明: 总结 前言 本地部署了大模型,下一步任务便是如何调用的问题,…...

20240708 每日AI必读资讯
🤖破解ChatGPT惊人耗电!DeepMind新算法训练提效13倍,能耗暴降10倍 - 谷歌DeepMind研究团队提出了一种加快AI训练的新方法——多模态对比学习与联合示例选择(JEST),大大减少了所需的计算资源和时间。 - JE…...
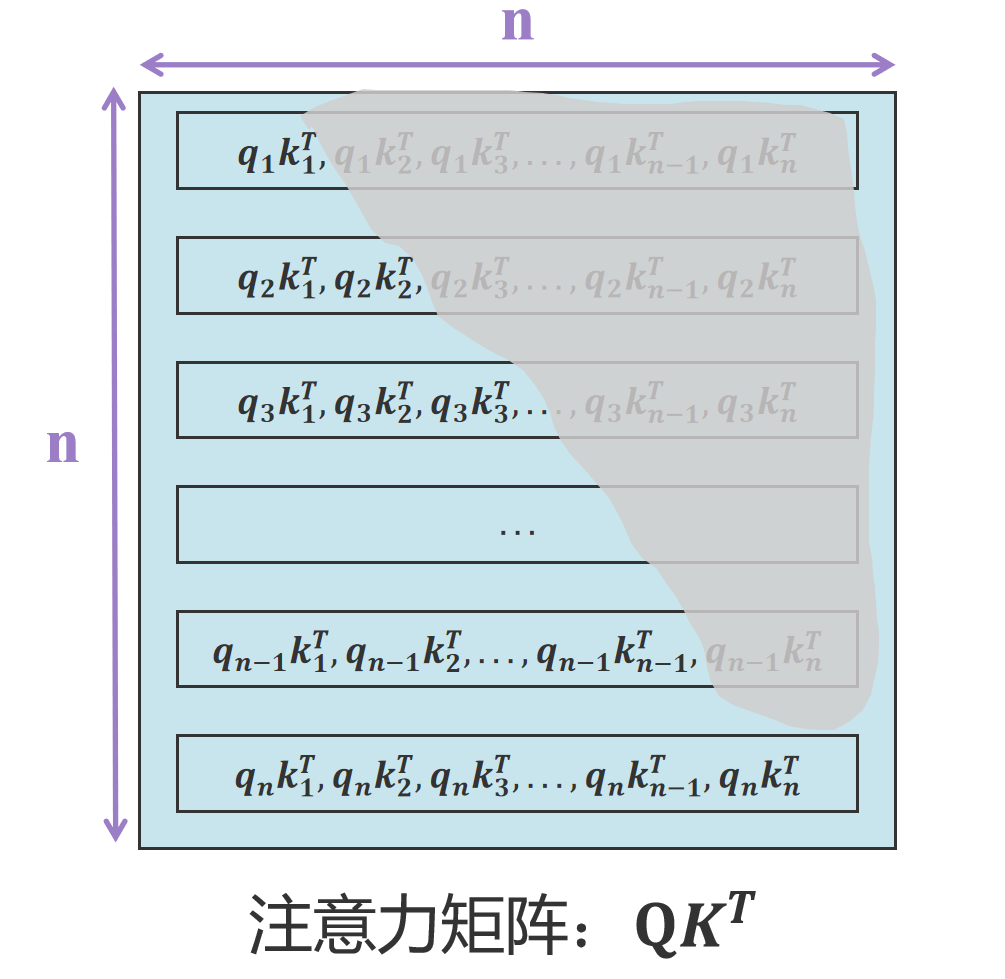
为什么KV Cache只需缓存K矩阵和V矩阵,无需缓存Q矩阵?
大家都知道大模型是通过语言序列预测下一个词的概率。假定{ x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x n − 1 x_{n-1} xn−1}为已知序列,其中 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x…...

VS code修改底部的行号的状态栏颜色
VSCode截图 相信很多小伙伴被底部的蓝色状态栏困扰很久了 处理的方式有两种: 1、隐藏状态栏 2、修改其背景颜色 第一种方法大伙都会,今天就使用第二种方法。 1、点击齿轮进入setting 2、我现在用的新版本,设置不是以前那种json格式展示&…...

【鸿蒙学习笔记】MVVM模式
官方文档:MVVM模式 [Q&A] 什么是MVVM ArkUI采取MVVM Model View ViewModel模式。 Model层:存储数据和相关逻辑的模型。View层:在ArkUI中通常是Component装饰组件渲染的UI。ViewModel层:在ArkUI中,ViewModel是…...

端、边、云三级算力网络
目录 端、边、云三级算力网络 NPU Arm架构 OpenStack kubernetes k3s轻量级Kubernetes kubernetes和docker区别 DCI(Data Center Interconnect) SD/WAN TF 端、边、云三级算力网络 算力网络从传统云网融合的角度出发,结合 边缘计算、网络云化以及智能控制的优势,通…...

java —— JSP 技术
一、JSP (一)前言 1、.jsp 与 .html 一样属于前端内容,创建在 WebContent 之下; 2、嵌套的 java 语句放置在<% %>里面; 3、嵌套 java 语句的三种语法: ① 脚本:<% java 代码 %>…...

【Python学习笔记】菜鸟教程Scrapy案例 + B站amazon案例视频
背景前摇(省流可以跳过这部分) 实习的时候厚脸皮请教了一位办公室负责做爬虫这块的老师,给我推荐了Scrapy框架。 我之前学过一些爬虫基础,但是用的是比较常见的BeautifulSoup和Request,于是得到Scrapy这个关键词后&am…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

华为云Flexus+DeepSeek征文 | MaaS平台避坑指南:DeepSeek商用服务开通与成本控制
作者简介 我是摘星,一名专注于云计算和AI技术的开发者。本次通过华为云MaaS平台体验DeepSeek系列模型,将实际使用经验分享给大家,希望能帮助开发者快速掌握华为云AI服务的核心能力。 目录 作者简介 前言 一、技术架构概览 1.1 整体架构设…...

如何使用CodeRider插件在IDEA中生成代码
一、环境搭建与插件安装 1.1 环境准备 名称要求说明操作系统Windows 11JetBrains IDEIntelliJ IDEA 2025.1.1.1 (Community Edition)硬件配置推荐16GB内存50GB磁盘空间 1.2 插件安装流程 步骤1:市场安装 打开IDEA,进入File → Settings → Plugins搜…...
