图论基础概念(详细讲解)
今天,我们讲解一下图论的概念,首先我们知道图是一个什么东西。
图你可以理解成一个网络系统,两个节点之间可能会有边,边链接两个节点,可能是有向(就比如说a只能往b,或者b只能往c),可能是无向(就是相当于没有方向,如果a和b有一条无向边的话,a可以往b,b可以往a),一条边可能有长度,我写一些图论题目常见的用词:
1.有向边:上面说了,他是有方向的,比如说a到b的有向边不能由b到a
2.无向边:上面说了,就是只要连上了两个都能到达
3.边权:代表边的长度,有些图可能不需要考虑边长,比如说判断两点是否可达这种问题是没有边权的。
4.反向边:只对有向边有效,比如说a->b,他的反向边就是b->a
5.重边:出现了两条一模一样的边,可能会影响后面的算法,所以说要注意(不过一般来讲,基础题是保证了没有重边,不过仍然需要注意)
6.自环:自己向自己连一条边,这种情况和重边一样的,也会影响算法,甚至可能让一些算法卡住。
7.链:对于任意一个节点,他们当中没有分叉,比如说这种:1->2,2->3这种,就有点像一条直线。这种数据可能需要小心,因为有些算法会在链上退化(比如说像BST(二叉搜索树)),不过有时候骗分的时候也可以特判链的情况。
8 .环:相当于把链的首尾相接,有时候环也会卡住。
9.树:这种数据比较友好,一些图的算法不会在上面退化,反倒还容易骗分一些,定义是:由n个节点和n-1条组成的无向无环图。
10.菊花图:就是所有点都连到了一个点,形成了一朵"菊花",有些算法会在上面退化,比如说spfa算法的O(km)会在菊花图的情况下变成O(nm)(这里一定要注意这种情况,以前NOI曾经有人写了spfa被菊花图卡了)
11.蒲公英图:菊花图和链组成起来,也会让一些算法退化。
12.负权/负权边:意思说一条边的权值为负数,这回让一些算法出问题(例如dijkstra最短路),这种时候必须要spfa算法了(当然不止这些,还有一些其他的算法也会在负权边上出问题)。
13.负权回路/负环:相当于一个环里所有数为负数,为让最短路算法卡进去(包括spfa),遇到负环可能需要用spfa判断负环.
14.正权回路/正环:根负环一样的,只不过是正数,这也会让求最长路时出问题
15.连通图:图是联通的,对于任意两点,他们都有一条路径。
16.点权:有一些题目,他不是边有长度,而是经过一个点有点权(比如说我经过一个点需要支付多少钱啊这种的),一般来讲,树形dp一般是没有边权而是点权。
相关文章:
)
图论基础概念(详细讲解)
今天,我们讲解一下图论的概念,首先我们知道图是一个什么东西。 图你可以理解成一个网络系统,两个节点之间可能会有边,边链接两个节点,可能是有向(就比如说a只能往b,或者b只能往c),可能是无向&a…...

未在本地计算机上注册“microsoft.ACE.oledb.12.0”提供程序报错的解决办法
今天在免费云服务器,三丰云上运行c#或python程序,都提示:未在本地计算机上注册“microsoft.ACE.oledb.12.0”提供程序,PHP程序就直接乱码,odbc_connect(): SQL error: [Microsoft][ODBC ���&…...

《从零开始学习Linux》——开篇
前言 近日笔者新开专栏,《从零开始学习Linux》,Linux水深而且大,学了一圈之后,有懂得有不懂的,一直没有机会整体的全部重新捋一遍,本专栏的目的是,带着大家包括我自己重新学习Linux一遍这些知识…...

3D工艺大师快速生成装配动画,驱动汽车工业装配流程革新
在现代制造业的一般生产流程中,车间装配环节是产品由蓝图迈向市场前至关重要的一道工序。随着产品结构的日益复杂化和个性化需求的不断增长,车间装配工作面临着前所未有的挑战。高精密度的装配要求、错综复杂的组件关系以及频繁变更的生产计划࿰…...

gateway
gateway核心概念 1. 路由(route) 路由是网关中最基础的部分,路由信息包括一个ID、一个目的URI、一组断言工厂、一组Filter组成。如果断言为真,则说明请求的URL 和 配置的路由匹配。 2. 断言(predicates) 断言函数允许开发者去定义匹配Htt…...

第一个ffmpeg程序
在进行使用ffmpeg进行编写程序时,首先要记得进行注册设备(avdevice_register_all ),程序运行时,只需要注册一次就可以 avdevice_register_all 是 FFmpeg 多媒体处理库中的一个函数,其作用是注册所有可用的音…...

论文翻译:Large Language Models for Education: A Survey and Outlook
https://arxiv.org/abs/2403.18105 目录 教育领域的大型语言模型:一项调查和展望摘要1. 引言2. 教育应用中的LLM2.1 概述2.2 学习辅助2.2.1 问题解决(QS) 2.2.2 错误纠正(EC)2.2.3 困惑助手(CH)…...
)
python为什么慢?(自用)
《Cython系列》1. Cython 是什么?为什么要有 Cython?为什么我们要用 Cython? - 古明地盆 - 博客园 (cnblogs.com) 古明地盆的主页 - 博客园 (cnblogs.com) 我原本认为,python慢的原因是“逐行解释程序并执行”,那么我…...

压缩感知3——重构算法正交匹配追踪算法
算法流程 问题的实质是:AX Y 求解(A是M维,Y是N维且N>>M并且稀疏度K<M)明显X有无穷多解,重构过程是M次采样得到的采样值升维的过程。OMP算法的具体步骤:(1)用X表示信号,初始化残差e0 …...

“好物”推荐+Xshell连接实例+使用Conda创建独立的Python环境
目录 主题:好易智算平台推荐RTX 4090DGPU实例租用演示安装配置torch1.9.1cuda11.1.1环境引言:算力的新时代平台介绍:技术与信任的结晶使用案例:实际使用展示创建实例开始使用连接实例(下文演示使用Xshell连接ÿ…...

浪潮天启防火墙TQ2000远程配置方法SSL-V偏、L2xx 配置方法
前言 本次设置只针对配置V偏,其他防火墙配置不涉及。建议把防火墙内外网都调通后再进行V偏配置。 其他配置可参考:浪潮天启防火墙配置手册 配置SSLVxx 在外网端口开启SSLVxx信息 开启SSLVxx功能 1、勾选 “启用SSL-Vxx” 2、设置登录端口号࿰…...

java八股文面试题
Java八股文面试题通常涵盖了Java语言的基础知识、高级特性、框架应用、数据库操作等多个方面。以下是一些常见的Java面试题及其详细回答,按照不同的主题进行分类: 一、Java基础 面向对象的特征有哪些? 抽象:忽略与当前目标无关的…...

【服务器】在Linux查看运行的Python程序,并找到特定的Python程序
在Linux查看运行的Python程序并找到特定的Python程序 写在最前面1. 使用ps命令查看所有Python进程查看详细信息 2. 使用pgrep命令查找Python进程ID 3. 使用top或htop命令使用top命令使用htop命令 4. 使用lsof命令查找Python进程打开的文件 5. 使用nvidia-smi命令查看GPU使用情况…...
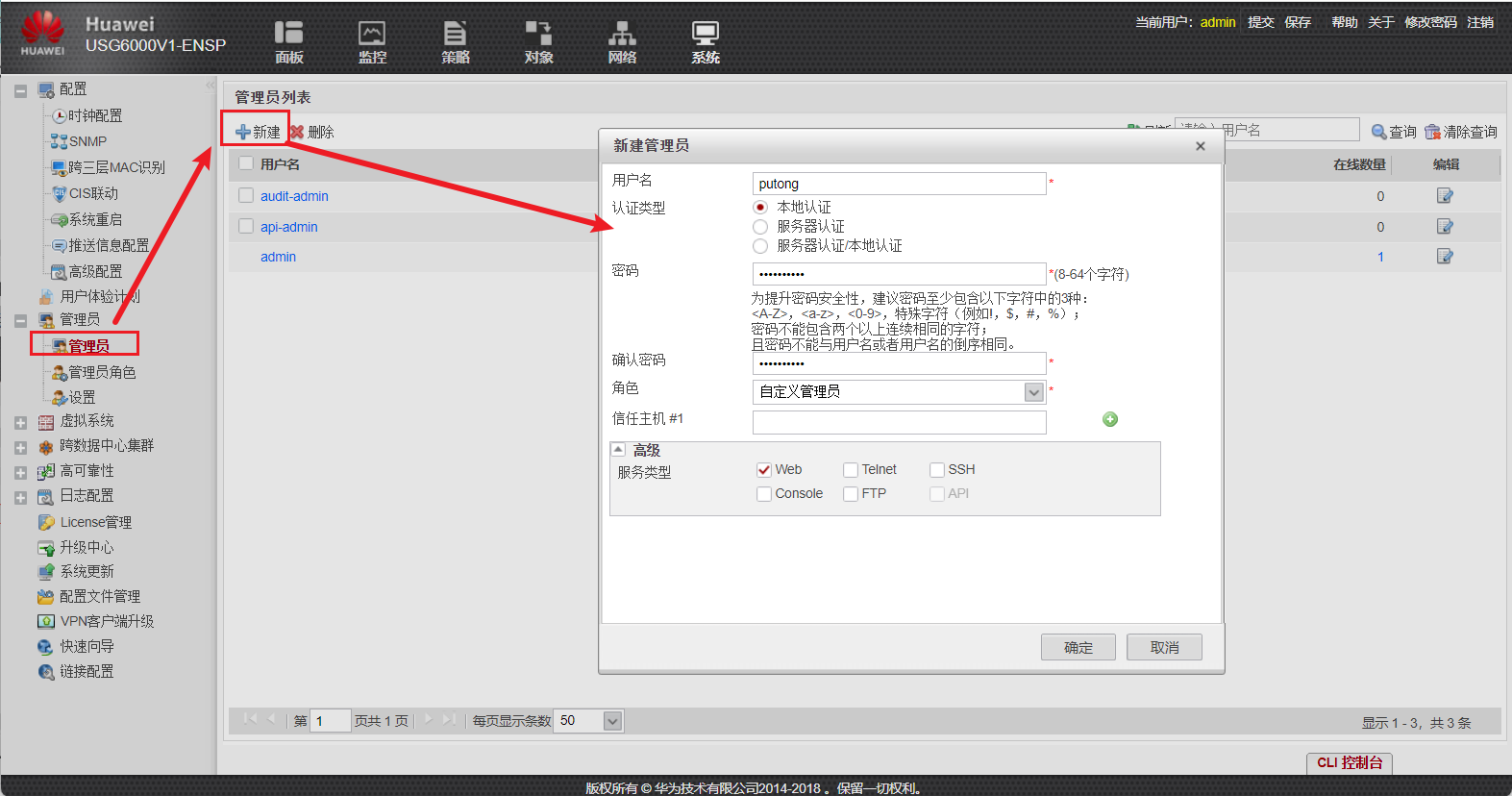
安全防御---防火墙实验1
安全防御—防火墙实验1 一、实验拓扑与要求 要求: 1、DMZ区内的服务器,办公区仅能在办公时间内(9:00-18:00)可以访问,生产区的设备全天可以访问 2、生产区不允许访问互联网,办公区和游客区允许访问互联网 …...

SpringBoot配置Swagger开启页面访问限制
在Spring Boot项目中配置Swagger时,开启页面访问限制通常意味着你希望控制哪些用户或角色可以访问Swagger UI文档页面。由于Swagger UI是一个静态资源,它本身并不直接支持基于角色的访问控制(RBAC)。但是,你可以通过Sp…...

前端代码基本逻辑-vue3
前端vue建立过程 安装nodejs 官网下载安装,并且记住安装路径,记得配置系统变量Path 安装VUE/CLI npm install -g vue/cli --全局安装vue 使用VUE/CLI生成代码框架 vue create your-project-name --我的your-project-name为web 运行项目 cd your-…...
怎么用PPT录制微课?详细步骤解析!
随着信息技术的不断发展,微课作为一种新型的教学形式,因其短小精悍、针对性强等特点,在教育领域得到了广泛的应用。而PPT作为一款常用的演示工具,不仅可以用来制作课件,还可以利用其内置的录屏功能或结合专业的录屏软件…...

Git使用方法
Git是一种分布式版本控制系统,它可以记录和管理软件开发过程中的变更。 Git的基本概念包括以下几个部分: 仓库(Repository):Git用仓库来存储项目的代码和历史记录。一个仓库可以包含多个分支。 分支(Bran…...

HTTP的请求报文和响应报文是怎样的,有哪些常见字段?
http报文分为请求报文和响应报文 请求报文包含:请求行、请求头、空行、、请求体 请求行包含: 方法:即要执行的操作,如get,post、put、delet 资源路径:请求的资源的URL HTTP版本:使用的http协议…...

自注意力简介
在注意力机制中,每个查询都会关注所有的键值对并生成一个注意力输出。如果查询q,键k和值v都来自于同一组输入,那么这个注意力就被称为是自注意力(self-attention)。自注意力这部分理论,我觉得台大李宏毅老师…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
