代码随想录算法训练营第十六天| 530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先
写代码的第十六天,自从到了二叉树错误版代码就少了,因为我自己根本没思路,都是看完思路在做,那基本上就是小语法问题,很少有其他问题了,证实了我好菜。。。。。。
还是得写思路啊啊啊啊,写思路好重要!!!
530.二叉搜索树的最小绝对差
思路
看见二叉搜索树,首先可以想到中序遍历,就变成了一个有序的数组,在数组中求相邻两个元素的最小绝对差。
class Solution:def getMinimumDifference(self, root: Optional[TreeNode]) -> int:mindif = float('inf')res = []self.traversal(root,res)for i in range(1,len(res)):diff = res[i] - res[i-1]mindif = min(mindif, diff)return mindifdef traversal(self,root,res):if root == None:return left = self.traversal(root.left,res)res.append(root.val)right = self.traversal(root.right,res)return res
思路(双指针)
要计算任意两个结点的最小值,还是按照左中右这样的顺序,因为这样计算的话每次都是从小到大的顺序,计算差值肯定相邻的一定比不相邻的小,在最开始我一直觉得万一最后一个数和第一个数的差值比其他的都小呢,其实这种情况根本不可能存在,就像上面的数组,最后一个数减去第一个数的差值不可能比他相邻的数减去第一个数的差值小。所以在这里设置两个结点变量,一个指向当前结点,一个指向当前结点的前一个结点,这两个结点都进行中序遍历,对这两个结点做减法,记录最小值,然后递归的进行中序遍历不断的判断,这个时候记录最小值的变量就应该设置为全局变量了,因为要存储最后的最小值,而不是每次递归都给他初始化成同一个值,它需要被记录。
正确代码:
class Solution:def __init__(self):self.mindif = float('inf')self.pre = Nonedef getMinimumDifference(self, root: Optional[TreeNode]) -> int:self.traversal(root)return self.mindifdef traversal(self,cur):if cur == None:returnself.traversal(cur.left)if self.pre != None:self.mindif = min(cur.val - self.pre.val,self.mindif)self.pre = curself.traversal(cur.right)
总结一下全局变量这一块,之前一直不知道全局变量用在哪,但是连着做了三四个题,我理解的全局变量就是在所有函数中进行操作这个变量他的值都会被存下来,会改变。如果放在函数体内的局部变量尤其是在递归的时候每次都会重复调用,如果像之前一样总是设置为0或者1这种,那么每次递归都从0或者1开始,肯定会报错。
501.二叉搜索树中的众数
思路
使用中序遍历(但其实好像哪种遍历都行,因为最后生成的是字典,不需要非得有序),在遍历过程中直接构建字典,然后遍历字典输出最大的那个value。
注释:如果你想将字典中所有键的初始值都设置为0,但不知道具体的键有哪些,你可以使用默认字典(defaultdict)来实现。defaultdict 是 collections 模块中的一个类,它是字典的一个子类,可以提供默认值来初始化字典中的键。
from collections import defaultdict
my_dict = defaultdict(lambda: 0)
错误第一版:第一处错误是在使用 defaultdict 初始化 mapdict 时,需要指定默认值的类型。你可以将 int 作为默认值类型,表示键的初始值为0。第二处错误是在遍历 mapdict 的键值对时,需要使用 items() 方法来获取键值对的迭代器,然后才能进行迭代。第三处错误是在 findMode() 方法中的 if root == None 分支中,你返回的是 None,而函数的返回类型应该是 List[int]。你可以返回一个空列表 [] 来表示没有找到任何模式。
from collections import defaultdict
class Solution:def findMode(self, root: Optional[TreeNode]) -> List[int]:result = []mapdict = defaultdict()if root == None:return self.searchBFS(root,mapdict)maxval = max(mapdict.values())for k,v in mapdict:if v == maxval:result.append(k)return resultdef searchBFS(self,root,mapdict):if root == None:return self.searchBFS(root.left,mapdict)mapdict[root.val] += 1self.searchBFS(root.right,mapdict)
正确代码:
from collections import defaultdict
class Solution:def findMode(self, root: Optional[TreeNode]) -> List[int]:result = []mapdict = defaultdict(int)if root == None:return []self.searchBFS(root,mapdict)maxval = max(mapdict.values())for k,v in mapdict.items():if v == maxval:result.append(k)return resultdef searchBFS(self,root,mapdict):if root == None:return self.searchBFS(root.left,mapdict)mapdict[root.val] += 1self.searchBFS(root.right,mapdict)
需要注意的一个地方是,众数可以有很多个,所以设置了result来存放。
思路(指针)
拿过来自己没思路,这个情况很烦啊,我一直想不通遍历的话不还是变成数组这样才能比较吗,指针就算是设置为一个cur一个pre和上面题一样也做不出来啊,怎么就判断这个是众数呢,就算判断了你怎么计数呢?这些问题我无法解决,我好痛苦。看了一下卡哥的思路,也是设置cur和pre两个指针,采用中序遍历,pre一直在cur前面,他俩永远是相邻的,只要判断这两个指针相等,那么这个数就出现了不止一次就可以说是众数,将其append进结果集中,但是如果当前遍历的众数出现了两次,但是之后有众数出现了三次,这种情况怎么解决呢,把当前结果集清空,然后将现在的结果append进结果姐,第一个问题解决了。那现在怎么计数呢,当出现pre和cur的值是相等的时候,count计数器加一,一旦pre和cur不相等count直接变成1,重新从1开始计数。记得要更新pre。
现在来解决递归的三个基本条件:
解决问题1:参数和返回值?我们设置了存储最后众数的结果集,pre指针,但是这些都已经设置在全局变量中了,所以参数只需要cur。因为要遍历完整颗树并不需要在过程中停止,所以不需要返回值,同时需要修改的值已经在全局变量中设置好了,也不需要返回。
解决问题2:终止条件?当cur为空的时候,就证明树遍历结束了,但是我们不需要返回值,所以return就行。
解决问题3:单层递归逻辑?pre在cur前面,不停的比较cur和pre的值,如果相等,将这个值append进result中,count也就是出现次数加一;当pre不等与cur的值的时候将count的值赋值给maxcount,然后将count=1,用这一步把现在出现的众数的出现最大次数计数,更新maxcount;然后继续遍历继续找,如果有出现count大于maxcount的情况的时候就把result全部清空,然后将新的这个结点的值append进result中,更新maxcount,直到终止条件。
错误第一版:
from collections import defaultdict
class Solution:def __init__(self):self.pre = Noneself.result = []self.count = 1self.maxcount = float('-inf')def traversal(self,cur):if cur == None:return self.traversal(cur.left)if self.pre != None and self.pre.val == cur.val:self.count += 1self.result.append(cur.val)if self.pre != None and self.pre.val != cur.val:self.maxcount = self.countself.count = 1if self.count > self.maxcount:self.result.clear()self.result.append(cur.val)self.traversal(cur.right)def findMode(self, root: Optional[TreeNode]) -> List[int]:self.traversal(root)return self.result
再次整理思路:只看单次递归这里,先计数在和maxcount比较,然后再决定要不要进result。如果pre和cur的值相等那么count+1,如果不相等,那么count=1;然后再将count和maxcount进行比较,如果count等于maxcount,那么将当前的结点值append进result,如果count小于maxcount不做任何操作,如果count大于maxcount那么更新maxcount = count并且将result全部清空,然后将现在的值append进result。
正确代码:
from collections import defaultdict
class Solution:def __init__(self):self.pre = Noneself.result = []self.count = 1self.maxcount = 0def traversal(self,cur):if cur == None:return self.traversal(cur.left)if self.pre != None and self.pre.val == cur.val:self.count += 1if self.pre != None and self.pre.val != cur.val:self.count = 1self.pre = curif self.count == self.maxcount:self.result.append(cur.val)if self.count > self.maxcount:self.maxcount = self.countself.result.clear() # 先清空 result 列表self.result.append(cur.val)self.traversal(cur.right)def findMode(self, root: Optional[TreeNode]) -> List[int]:self.traversal(root)return self.result
236. 二叉树的最近公共祖先
思路
因为是想找最近公共祖先,所以后序遍历最好。(没审题我真的会谢,我一直挣扎与万一p或者q不在这个树中咋办啊,结果题里面写了p 和 q 均存在于给定的二叉树中,我真该啊。。。)
解决问题1:参数和返回值是什么?在本题中参数是root以及p和q两个结点,返回值就是最近公共祖先。
解决问题2:终止条件是什么?如果在遍历的过程中在左子树出现q右子树出现p或者左子树出现p右子树出现q那么就说明公共祖先存在,返回此时左右子树的上一个,也就是左右中遍历的中结点;如果遍历了整颗树(也就是root==None的情况)只存在一个或者两个都不存在,那么返回None,没有公共祖先。
解决问题3:单次递归的逻辑是什么?根据下面的解释,本题中单次递归是左右都需要遍历的,并且需要返回值的。按照后序遍历左右中的情况,先递归左子树,然后递归右子树,最后处理中结点,其实中结点是我们的主要处理位置。中结点需要判断的是其左右子树是否存在q和p,如果两个都存在,那么向上一层返回
补充:这个部分是我经常会产生疑问的,卡哥说的非常清晰,记一下嘿嘿嘿。



错误第一版:就因为挣扎于万一有p或者q不在树中怎么办,其实题中说的很明确了,q和p一定存在。错误是解答错误,思路还是有点问题。
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if root == None:return left = self.lowestCommonAncestor(root.left,p,q)right = self.lowestCommonAncestor(root.right,p,q)if left != None and right == None:return rightelif left == None and right != None:return leftelse:return root
重新整理思路:在终止条件这里,一种情况是遍历完整颗树也就是root==None的时候那么返回root其实也就是None(需要注意一下我之前理解的终止条件总以为是最后的输出值,其实不是,他就只是最后一次递归的值,我们还要回溯回去呢),第二种情况就是当root结点就是q或者p的时候根据题意p和q是一定存在的,那么当前已经遍历到了q或者p那就证明剩下的那个一定在他下面的树中,所以q或者p就是他们自己的公共祖先。再说一下单次递归这里,如果遍历了left和right但是这两个里面都是有返回值的,也就是存在p或q那么就直接返回root也就是他们的上一个结点,如果只有left或者right有值,那就证明p和q存在于一侧,所以只返回那一侧就可以了,如果遍历完成了没有任何一个地方存在,那就返回None。
正确代码:
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if root == None:return rootif root == q or root == p:return rootleft = self.lowestCommonAncestor(root.left,p,q)right = self.lowestCommonAncestor(root.right,p,q)if left != None and right == None:return leftelif left == None and right != None:return rightelif left != None and right != None:return rootelse:return None
相关文章:

代码随想录算法训练营第十六天| 530.二叉搜索树的最小绝对差、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先
写代码的第十六天,自从到了二叉树错误版代码就少了,因为我自己根本没思路,都是看完思路在做,那基本上就是小语法问题,很少有其他问题了,证实了我好菜。。。。。。 还是得写思路啊啊啊啊,写思路好…...

NODEJS复习(ctfshow334-344)
NODEJS复习 web334 下载源码代码审计 发现账号密码 代码逻辑 var findUser function(name, password){ return users.find(function(item){ return name!CTFSHOW && item.username name.toUpperCase() && item.password password; }); }; 名字不等于ctf…...

【Go系列】RPC和grpc
承上启下 介绍完了Go怎么实现RESTFul api,不可避免的,今天必须得整一下rpc这个概念。rpc是什么呢,很多人都想把rpc和http一起对比,但是他们不是一个概念。RPC是一种思想,可以基于tcp,可以基于udp也可以基于…...

【VUE】v-if和v-for的优先级
v-if和v-for v-if 用来显示和隐藏元素 flag为true时,dom元素会被删除达到隐藏效果 <div class"boxIf" v-if"flag"></div>v-for用来进行遍历,可以遍历数字对象数组,会将整个元素遍历指定次数 <!-- 遍…...

【单目3D检测】smoke(1):模型方案详解
纵目发表的这篇单目3D目标检测论文不同于以往用2D预选框建立3D信息,而是采取直接回归3D信息,这种思路简单又高效,并不需要复杂的前后处理,而且是一种one stage方法,对于实际业务部署也很友好。 题目:SMOKE&…...

数据库系统概论:数据库系统的锁机制
引言 锁是计算机协调多个进程或线程并发访问某一资源的机制。在数据库中,数据作为一种共享资源,其并发访问的一致性和有效性是数据库必须解决的问题。锁机制通过对数据库中的数据对象(如表、行等)进行加锁,以确保在同…...
-- ADB获取设备信息)
Django+vue自动化测试平台(28)-- ADB获取设备信息
概述 adb的全称为Android Debug Bridge,就是起到调试桥的作用。通过adb可以在Eclipse中通过DDMS来调试Android程序,说白了就是调试工具。 adb的工作方式比较特殊,采用监听Socket TCP 5554等端口的方式让IDE和Qemu通讯,默认情况下…...
RESTful API设计指南:构建高效、可扩展和易用的API
文章目录 引言一、RESTful API概述1.1 什么是RESTful API1.2 RESTful API的重要性 二、RESTful API的基本原则2.1 资源导向设计2.2 HTTP方法的正确使用 三、URL设计3.1 使用名词而非动词3.2 使用复数形式表示资源集合 四、请求和响应设计4.1 HTTP状态码4.2 响应格式4.2.1 响应实…...

npm下载的依赖包版本号怎么看
npm下载的依赖包版本号怎么看 版本号一般分三个部分,主版本号、次版本号、补丁版本号。 主版本号:一般依赖包发生重大更新时,主版本号才回发生变化,如Vue2.x到Vue3.x。次版本号:当依赖包中发生了一些小变化ÿ…...
css前端面试题
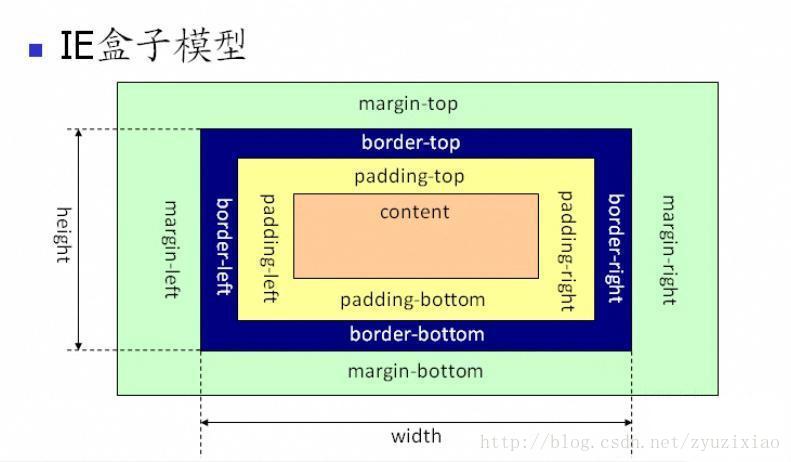
1.什么是css盒子模型? 盒子模型包含了元素内容(content)、内边距(padding)、边框(border)、外边距(margin)几个要素。 标准盒子模型和IE盒子模型的区别在于其对元素的w…...

Vue从零到实战
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 非常期待和您一起在这个小…...

【Chatgpt大语言模型医学领域中如何应用】
随着人工智能技术 AI 的不断发展和应用,ChatGPT 作为一种强大的自然语言处理技术,无论是 自然语言处理、对话系统、机器翻译、内容生成、图像生成,还是语音识别、计算机视觉等方面,ChatGPT 都有着广泛的应用前景。特别在临床医学领…...
)
ES6 正则的扩展(十九)
1. 正则表达式字面量改进 特性:在 ES6 中,正则表达式字面量允许在字符串中使用斜杠(/)作为分隔符。 用法:简化正则表达式的书写。 const regex1 /foo/; const regex2 /foo/g; // 全局搜索2. u 修饰符(U…...

<数据集>钢铁缺陷检测数据集<目标检测>
数据集格式:VOCYOLO格式 图片数量:1800张 标注数量(xml文件个数):1800 标注数量(txt文件个数):1800 标注类别数:6 标注类别名称:[crazing, patches, inclusion, pitted_surface, rolled-in_scale, scr…...

Kafka系列之:Kafka存储数据相关重要参数理解
Kafka系列之:Kafka存储数据相关重要参数理解 一、log.segment.bytes二、log.retention.bytes三、日志段四、log.retention.check.interval.ms五、数据底层文件六、index、log、snapshot、timeindex、leader-epoch-checkpoint、partition.metadata一、log.segment.bytes 参数lo…...

Template execution failed: ReferenceError: name is not defined
问题 我们使用了html-webpack-plugin(webpack)进行编译html,导致的错误。 排查结果 连接地址 html-webpack-plugin版本低(2.30.1),html模板里面不能有符号,注释都不行 // var reg new RegExp((^|&)${name}([^&…...

CVE-2024-24549 Apache Tomcat - Denial of Service
https://lists.apache.org/thread/4c50rmomhbbsdgfjsgwlb51xdwfjdcvg Apache Tomcat输入验证错误漏洞,HTTP/2请求的输入验证不正确,会导致拒绝服务,可以借助该漏洞攻击服务器。 https://mvnrepository.com/artifact/org.apache.tomcat.embed/…...

Linux下如何安装配置Graylog日志管理工具
Graylog是一个开源的日志管理工具,可以帮助我们收集、存储和分析大量的日志数据。它提供了强大的搜索、过滤和可视化功能,可以帮助我们轻松地监控系统和应用程序的运行情况。 在Linux系统下安装和配置Graylog主要包括以下几个步骤: 准备安装…...

「MQTT over QUIC」与「MQTT over TCP」与 「TCP 」通信测试报告
一、结论 在实车5G测试中「MQTT Over QUIC」整体表现优于「TCP」,可在系统架构升级时采用MQTT Over QUIC替换原有的TCP通讯;从实现原理上基于QUIC比基于TCP在弱网、网络抖动导致频繁重连场景延迟更低。 二、测试方案 网络类型:实车5G、实车…...

获取磁盘剩余容量-----c++
获取磁盘剩余容量 #include <filesystem>struct DiskSpaceInfo {double total;double free;double available; };DiskSpaceInfo getDiskSpace(const std::string& path) {std::filesystem::space_info si std::filesystem::space(path);DiskSpaceInfo info;info.…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
