自动驾驶-预测概览
通过生成一条路径来预测一个物体的行为·，在每一个时间段内，为每一辆汽车重新计算预测他们新生成的路径，这些预测路径为规划阶段做出决策提供了必要信息
预测路径有实时性的要求，预测模块能够学习新的行为。我们可以使用多源的数据进行训练，可以是算法随着时间的推移而提升预测能力
有两种基本的预测类型，一种是基于模型的，一种是数据驱动的。预测将称为决策的核心，因为只要你知道该期待什么，就会做出更好的决策
基于模型的方法优点在于直观，结合了我们现有的物理知识以及交通法规还有人类行为
基于车道的预测
apollo提供了一种基于车道序列的方法
预测更关心在不同区域的转换，而不是某个区域内的具体行为
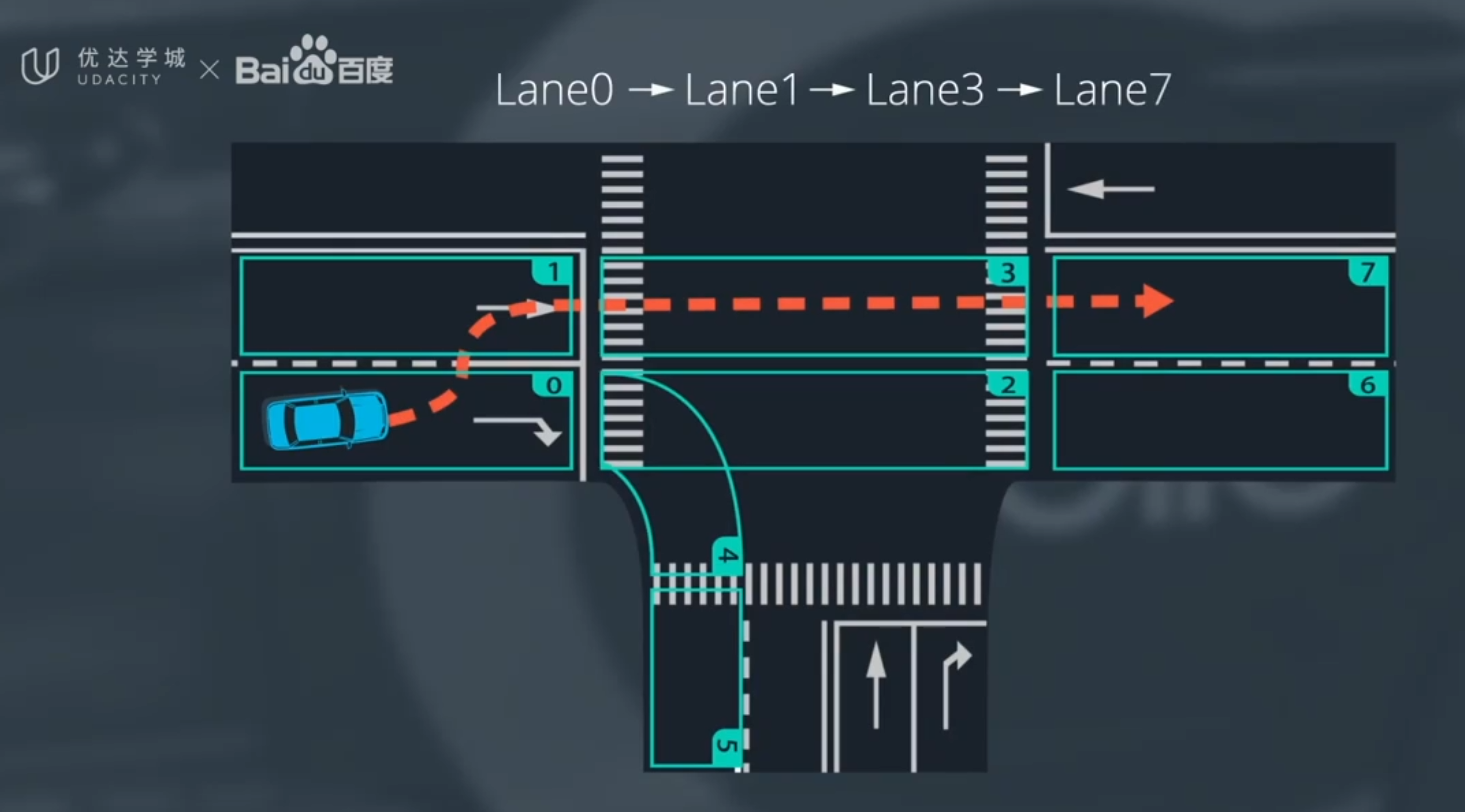
通过观察一个物体的朝向，位置和速度来预测它将会做什么
使用车道序列框架目标是为道路上的物体生成轨迹，这是很复杂的。
可以将预测问题简化为选择问题，选择车辆最有可能采取的车道顺序，可以通过计算每个车道序列的概率进行选择。 我们需要一个模型，将车辆状态和车道段输入，该模型提供车辆可能采取每个车道序列的概率
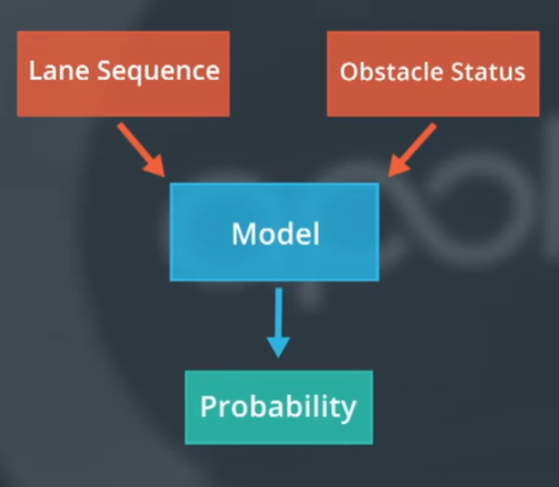
递归神经网络RNN
是一种利用时间序列数据特征的一种预测方法
神经网络的中间层将提取特征，例如轮胎和窗户。 神经网络从数据中学习的方式叫做后向传播
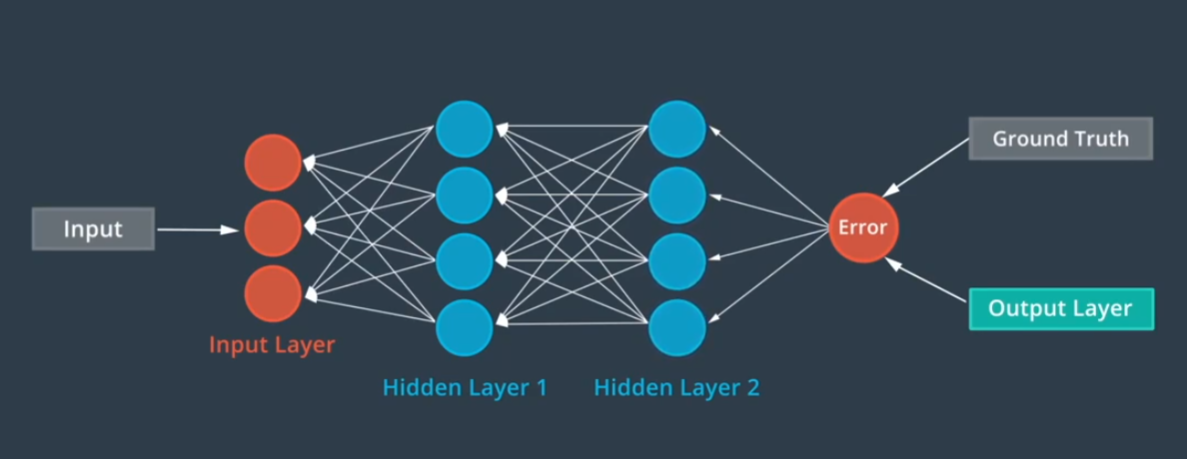
以上简称MLP，MLP从数据序列中提取出高级特征，每个MLP单元将序列的一个元素作为输入，并预测序列的下一个元素作为输出。为了对元素之间的顺序关系建立模型，每个单元之间建立一个额外的连接。意味着每个单元根据原始输入和前一个单元的输出进行预测
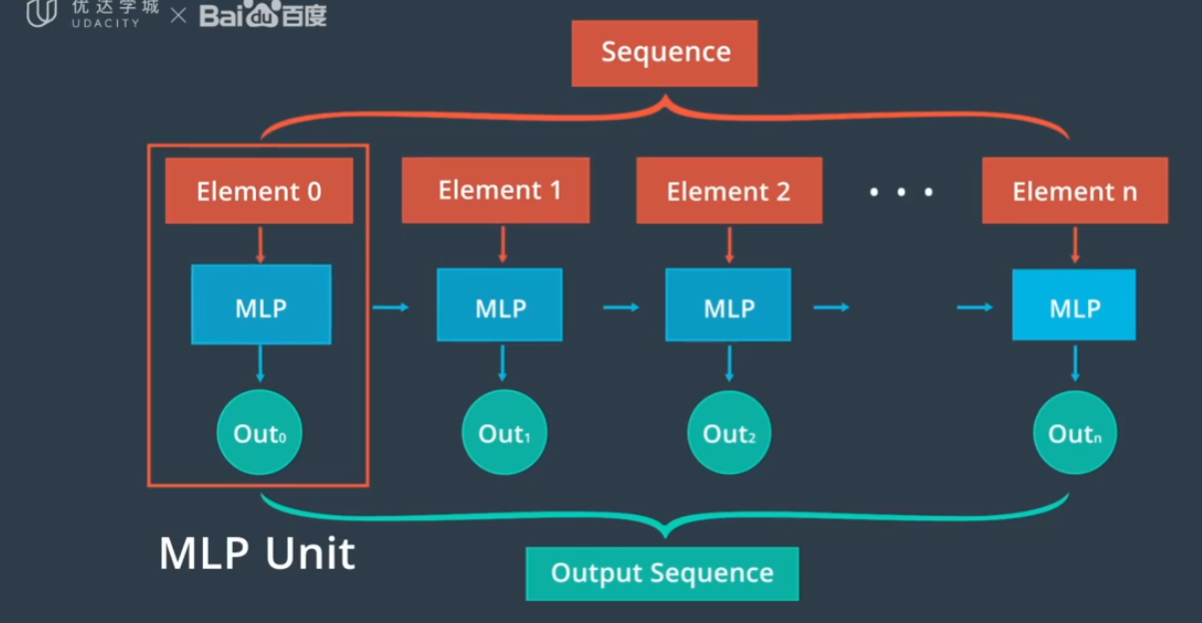
apollo使用RNN建立一个模型来预测车辆的目标车道。
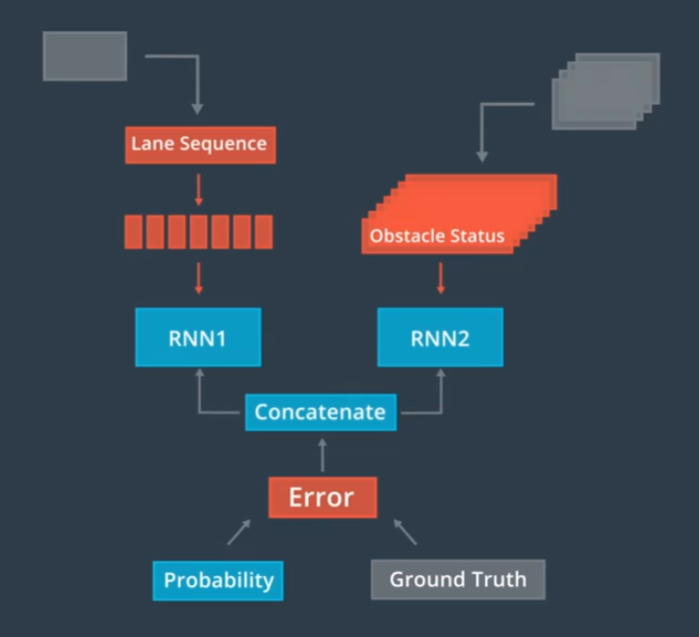
轨迹生成
一旦我们预测到物体的车道序列，就可以预测物体的轨迹。
先通过设置约束条件来去除大部分候选轨迹
使用初始状态和最终状态来拟合一个多项式模型，这种多项式足以进行预测
相关文章：
自动驾驶-预测概览
通过生成一条路径来预测一个物体的行为，在每一个时间段内，为每一辆汽车重新计算预测他们新生成的路径，这些预测路径为规划阶段做出决策提供了必要信息 预测路径有实时性的要求，预测模块能够学习新的行为。我们可以使用多源的数据…...
基于PSO算法优化PID参数的一些问题
目录 前言 Q1：惯性权重ω如何设置比较好？学习因子C1和C2如何设置？ Q2：迭代速度边界设定一定能够遍历（/覆盖）整个PID参数二维空间范围吗？还是说需要与迭代次数相关？迭代次数越高&a…...
什么是决策树？
1. 什么是决策树？ 决策树（Decision Tree）是一种常用的机器学习算法，用于解决分类和回归问题。它通过构建树结构来表示决策过程，分支节点表示特征选择，叶节点表示类别或回归值。 2. 决策树的组成部分 决策…...
ASP 快速参考
ASP 快速参考 概述 ASP（Active Server Pages）是一种由微软开发的服务器端脚本环境，用于动态网页设计和开发。它允许开发者创建和运行动态交互性网页，如访问数据库、发送电子邮件等。ASP页面通常以.asp为文件扩展名，并…...
(二)原生js案例之数码时钟计时
原生js实现的数字时间上下切换显示时间的效果，有参考相关设计，思路比较难，代码其实很简单 效果 代码实现 必要的样式 <style>* {padding: 0;margin: 0;}.content{/* text-align: center; */display: flex;align-items: center;justif…...
[CSS] 浮动布局的深入理解与应用
文章目录 浮动的简介元素浮动后的特点解决浮动产生的影响浮动后的影响解决浮动产生的影响 浮动相关属性实际应用示例示例1：图片与文字环绕示例2：多列布局示例3：响应式布局 总结 浮动布局是CSS中一种非常强大的布局方式，最初设计用…...
Linux云计算 |【第一阶段】ENGINEER-DAY2
主要内容： 磁盘空间管理fdisk、parted工具、开机自动挂载、文件系统、交换空间 KVM虚拟化 实操前骤： 1）添加一块硬盘（磁盘），需要关机才能进行操作，点击左下角【添加硬件】 2）选择2…...
9.11和9.9哪个大？
没问题 文心一言 通义千问...
学懂C语言（十二）：C语言中的二进制原理及应用
目录 1. 二进制原理 1.1 什么是二进制？ 1.2 如何在C语言中表示二进制？ 2. 二进制的表示 2.1 二进制和其他进制的转换 2.2 C语言中的二进制表示 3. 二进制运算 3.1 位运算符 3.2 计算过程示例 4. 应用示例 4.1 使用位运算实现开关 5. 总结 C语…...
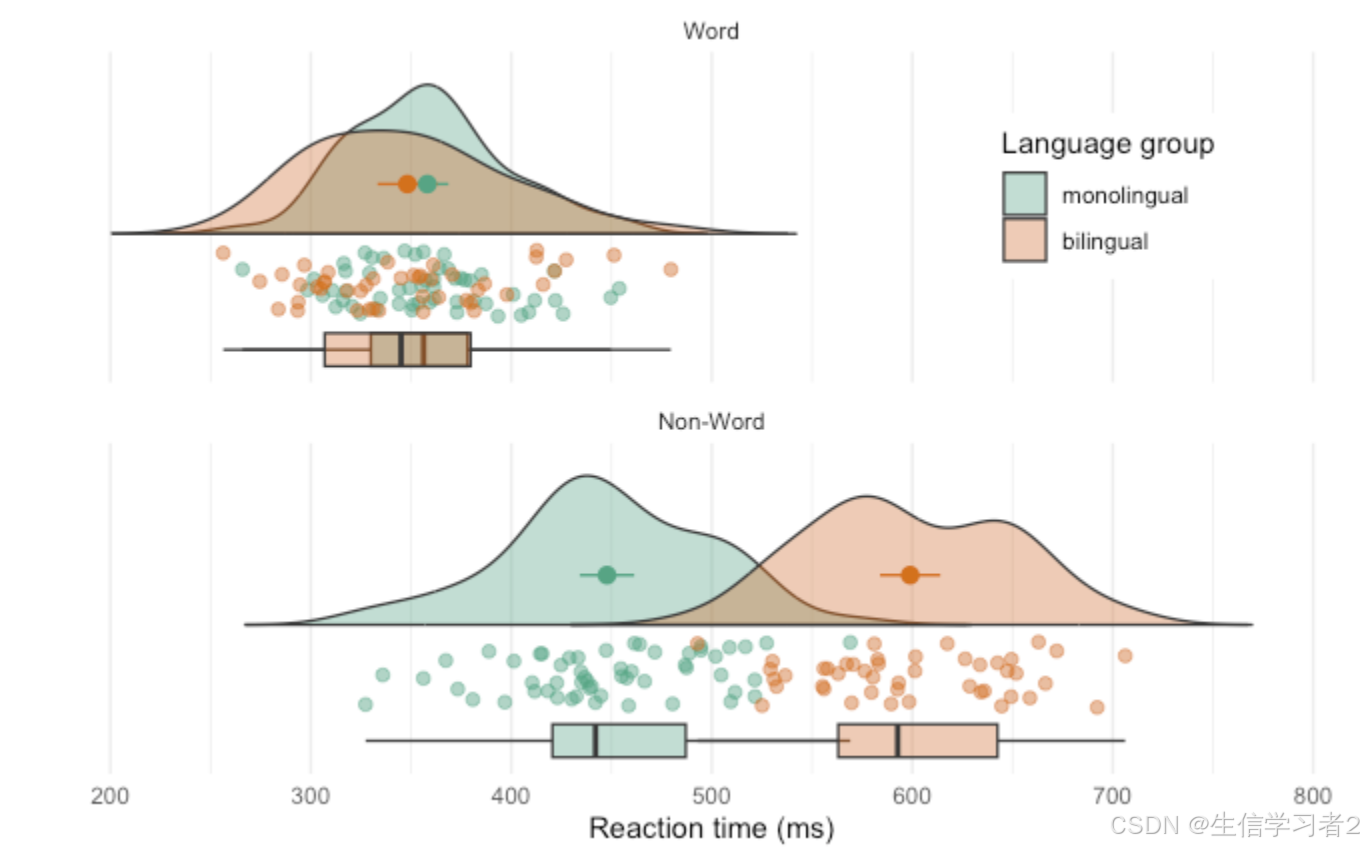
科研绘图系列：R语言雨云图（Raincloud plot）
介绍 雨云图（Raincloud plot）是一种数据可视化工具，它结合了多种数据展示方式，旨在提供对数据集的全面了解。雨云图通常包括以下几个部分： 密度图（Density plot）：表示数据的分布情况，密度图的曲线可以展示数据在不同数值区间的密度。箱线图（Box plot）：显示数据的中…...
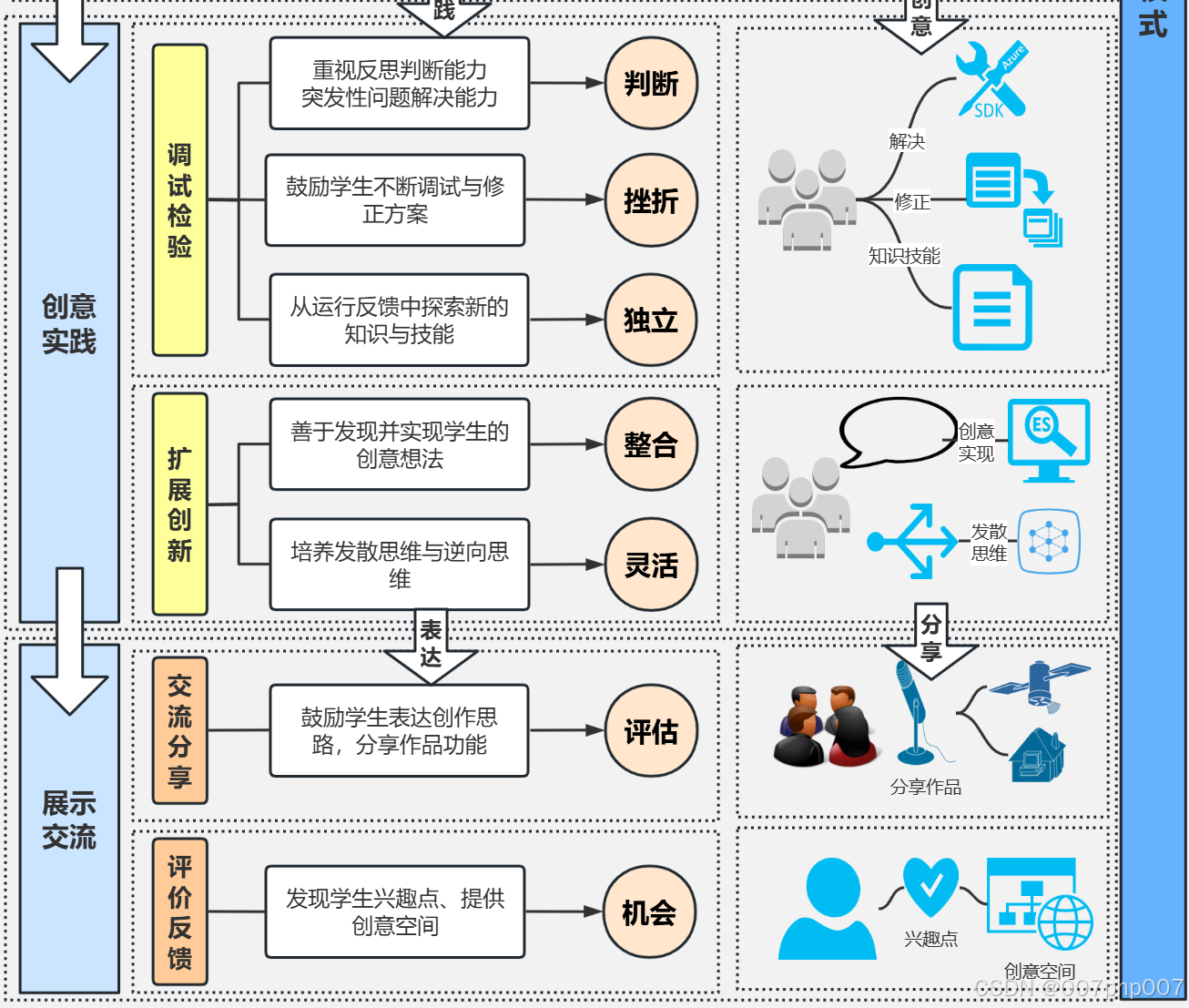
优化教学流程和架构：构建高效学习环境的关键步骤
在教育领域，设计和优化教学流程和架构是提高学习效果和学生参与度的关键。本文将探讨如何通过合理的教学流程和有效的架构来构建一个高效的学习环境。 ### 1. 理解教学流程和架构的重要性 教学流程指的是教学活动的组织和顺序，而教学架构则是指支持教学…...
js | this 指向问题
https://juejin.cn/post/6844904083707396109 任何函数运行的时候，都会创建一个context对象，context对象有一个this对象，在运行的时候决定。任何函数都对应一个reference类结构体（具体叫啥有点忘了），简单就…...
《昇思 25 天学习打卡营第 15 天 | 基于MindNLP+MusicGen生成自己的个性化音乐 》
《昇思 25 天学习打卡营第 15 天 | 基于MindNLPMusicGen生成自己的个性化音乐 》 活动地址：https://xihe.mindspore.cn/events/mindspore-training-camp 签名：Sam9029 MusicGen概述 MusicGen是由Meta AI的Jade Copet等人提出的一种基于单个语言模型&…...
Gitee 使用教程1-SSH 公钥设置
一、生成 SSH 公钥 1、打开终端（Windows PowerShell 或 Git Bash），通过命令 ssh-keygen 生成 SSH Key： ssh-keygen -t ed25519 -C "Gitee SSH Key" 随后摁三次回车键（Enter） 2、查看生成的 SSH…...
理解Cookie、Session和Token
在现代Web开发中，用户身份认证和会话管理是至关重要的部分。理解Cookie、Session和Token的区别和应用场景，有助于我们设计出更加安全和高效的Web应用。本文将详细探讨这三者的工作原理、优缺点以及使用场景。 1. Cookie 1.1 什么是Cookie？ …...
概率论原理精解【1】
文章目录 测度概述集类笛卡尔积定义例子 多集合的笛卡尔积定义计算方法注意事项 有限笛卡尔积的性质1. 定义2. 性质2.1 基数性质2.2 空集性质2.3 不满足交换律2.4 不满足结合律2.5 对并和交运算满足分配律 3. 示例4. 结论 参考链接 测度 概述 所谓测度，通俗的讲就…...
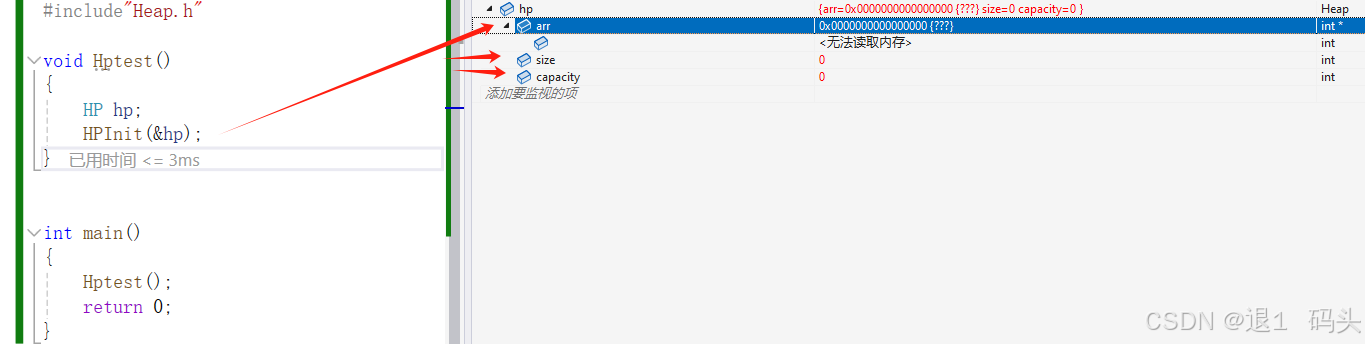
数据结构（二叉树-1）
文章目录 一、树 1.1 树的概念与结构 1.2 树的相关术语 1.3 树的表示 二、二叉树 2.1 二叉树的概念与结构 2.2特殊的二叉树 满二叉树 完全二叉树 2.3 二叉树的存储结构 三、实现顺序结构二叉树 3.1 堆的概念与结构 3.2 堆的实现 Heap.h Heap.c 默认初始化堆 堆的销毁 堆的插入 …...
巴黎奥运会倒计时 一个非常不错的倒计时提醒
巴黎奥运会还有几天就要开幕了，大家应该到处都可以看到巴黎奥运会的倒计时，不管是电视上，还是网络里，一搜索奥运会，就会看到。倒计时其实是一个我们在生活中很常用的一个方法，用来做事情的提醒，…...
【Python】使用库 -- 详解
库就是别人已经写好了的代码，可以让我们直接拿来用。 一个编程语言能不能流行起来，一方面取决于语法是否简单方便容易学习，一方面取决于生态是否完备。所谓的 “生态” 指的就是语言是否有足够丰富的库，来应对各种各样的场景。在…...
Web3D：WebGL为什么在渲染性能上输给了WebGPU。
WebGL已经成为了web3D的标配，市面上有N多基于webGL的3D引擎，WebGPU作为挑战者，在渲染性能上确实改过webGL一头，由于起步较晚，想通过这个优势加持，赶上并超越webGL仍需时日。 贝格前端工场为大家分享一下这…...
网络编程（Modbus进阶）
思维导图 Modbus RTU（先学一点理论） 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议，由 Modicon 公司（现施耐德电气）于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？
编辑：陈萍萍的公主一点人工一点智能 未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战，在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
XCTF-web-easyupload
试了试php，php7，pht，phtml等，都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接，得到flag...
无法与IP建立连接，未能下载VSCode服务器
如题，在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈，发现是VSCode版本自动更新惹的祸！！！ 在VSCode的帮助->关于这里发现前几天VSCode自动更新了，我的版本号变成了1.100.3 才导致了远程连接出…...
vscode（仍待补充）
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh？ debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指：像函数调用/返回一样轻量地完成任务切换。 举例说明： 当你在程序中写一个函数调用： funcA() 然后 funcA 执行完后返回&…...
解锁数据库简洁之道：FastAPI与SQLModel实战指南
在构建现代Web应用程序时，与数据库的交互无疑是核心环节。虽然传统的数据库操作方式（如直接编写SQL语句与psycopg2交互）赋予了我们精细的控制权，但在面对日益复杂的业务逻辑和快速迭代的需求时，这种方式的开发效率和可…...
【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课，做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程，它的核心机制是 Goroutine 协程、Channel 通道，并基于CSP（Communicating Sequential Processes࿰…...
C++ 基础特性深度解析
目录 引言 一、命名空间（namespace） C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用（reference） C 中的引用 与 C 语言的对比 四、inline（内联函数…...
Java 加密常用的各种算法及其选择
在数字化时代，数据安全至关重要，Java 作为广泛应用的编程语言，提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景，有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...