Laravel Dusk:点亮自动化测试的明灯
Laravel Dusk:点亮自动化测试的明灯
在Web开发中,确保应用程序的用户体验和功能正确性至关重要。Laravel Dusk是一个强大的浏览器自动化测试工具,它允许开发者模拟用户与应用程序的交互,从而进行端到端的测试。本文将深入探讨Laravel Dusk测试工具的工作原理,并通过实际代码示例,展示如何使用Dusk进行自动化测试。
Laravel Dusk测试工具概述
浏览器自动化测试的重要性
浏览器自动化测试可以模拟真实用户的操作,包括点击、输入、导航等,帮助开发者发现界面和功能上的问题。
Laravel Dusk的特点
- 真实浏览器:Dusk在真实的浏览器中运行测试,而不是使用无头浏览器。
- 易于编写:使用简单的API编写测试脚本。
- 截图和视频:测试失败时自动截图和录制视频,方便调试。
Dusk测试的工作原理
环境配置
Dusk需要一些特定的环境配置,包括安装ChromeDriver和配置Laravel环境变量。
测试用例编写
编写测试用例,使用Dusk提供的API模拟用户操作。
测试执行
使用PHPUnit运行测试,Dusk将控制浏览器执行测试用例。
结果验证
检查测试是否通过了所有的断言,并根据截图和视频进行问题定位。
实际代码示例
1. 安装和配置Dusk
首先,需要安装Dusk组件,并进行基本配置。
composer require --dev laravel/dusk
php artisan dusk:install
接着,配置.env文件,设置ChromeDriver路径等。
DUSK_DRIVER=chrome
CHROME_DRIVER_BINARY=/path/to/chromedriver
2. 编写测试用例
创建一个Dusk测试用例,模拟用户登录操作。
<?phpnamespace Tests\Browser;use App\User;
use Laravel\Dusk\Browser;
use Tests\DuskTestCase;class LoginTest extends DuskTestCase
{/** @test */public function userCanLogin(){$user = User::find(1);$this->browse(function (Browser $browser) use ($user) {$browser->visit('/login')->type('email', $user->email)->type('password', 'password')->press('Login')->assertPathIs('/home');});}
}
3. 运行测试
使用PHPUnit命令运行Dusk测试。
./vendor/bin/phpunit --filter DuskTestCase
高级Dusk测试技巧
等待元素
Dusk提供了等待元素出现的功能,以应对异步加载的情况。
$browser->waitForText('Welcome Back!');
断言
使用Dusk的断言方法验证页面元素和状态。
$browser->assertSee('Welcome Back!')->assertInputValue('email', $user->email);
模拟JavaScript事件
Dusk可以模拟JavaScript事件,如点击、滚动等。
$browser->script('window.scrollTo(0, document.body.scrollHeight);');
测试数据库事务
确保Dusk测试是数据库事务安全的。
protected function runTest()
{$this->beginDatabaseTransaction();parent::runTest();
}
结论
Laravel Dusk是一个功能强大的浏览器自动化测试工具,它通过模拟真实用户的浏览器操作,帮助开发者发现和修复应用程序中的问题。本文详细介绍了Dusk的工作原理,并通过实际代码示例,展示了如何编写和运行Dusk测试。
Dusk测试不仅提高了测试的准确性和效率,还通过截图和视频记录功能,方便了问题的定位和调试。掌握Dusk的使用,将为Web应用程序的质量保证提供有力支持。
本文的探讨和示例旨在为读者提供一个关于Laravel Dusk测试工具的全面指南,希望能够激发读者对浏览器自动化测试的兴趣,并在实际工作中应用这些知识。
相关文章:

Laravel Dusk:点亮自动化测试的明灯
Laravel Dusk:点亮自动化测试的明灯 在Web开发中,确保应用程序的用户体验和功能正确性至关重要。Laravel Dusk是一个强大的浏览器自动化测试工具,它允许开发者模拟用户与应用程序的交互,从而进行端到端的测试。本文将深入探讨Lar…...
Git、Gitlab以及分支管理
分布式版本控制系统 一、Git概述 Git是一种分布式版本控制系统,用于跟踪和管理代码的变更。它由Linus torvalds创建的,最初被设计用于Linux内核的开发。Git 允许开发人员跟踪和管理代码的版本,并且可以在不同的开发人员之间进行协作。 Githu…...

TCP/IP 协议栈介绍
TCP/IP 协议栈介绍 1. 引言 TCP/IP(传输控制协议/互联网协议)是一组用于数据网络中通信的协议集合,它是互联网的基础。本文将详细介绍TCP/IP协议栈的各个层次、工作原理以及其在网络通信中的作用。 2. TCP/IP 协议栈的层次结构 TCP/IP协议…...

香橙派orangepi系统没有apt,也没有apt-get,也没有yum命令,找不到apt、apt-get、yum的Linux系统
以下是一个关于如何在 Orange Pi 上的 Arch Linux 系统中发现缺失包管理器的问题并解决的详细教程。 发现问题 确认系统类型: 使用以下命令检查当前的 Linux 发行版: uname -a cat /etc/os-release如果你看到类似于 “Arch Linux” 的信息,说…...
在invidia jetpack4.5.1上运行c++版yolov8(tensorRT)
心路历程(可略过) 为了能在arm64上跑通yolov8,我试过很多很多代码,太多对库版本的要求太高了; 比如说有一个是需要依赖onnx库的,(https://github.com/UNeedCryDear/yolov8-opencv-onnxruntime-…...

Vue3 接入 i18n 实现国际化多语言
在 Vue.js 3 中实现网页的国际化多语言,最常用的包是 vue-i18n。 第一步,安装一个 Vite 下使用 <i18n> 标签的插件:unplugin-vue-i18n npm install unplugin-vue-i18n # 或 yarn add unplugin-vue-i18n 安装完成后,调整 v…...

深度学习环境坑。
前面装好了之后装pytorch之后老显示gpufalse。 https://www.jb51.net/article/247762.htm 原因就是清华源的坑。 安装的时候不要用conda, 用pip命令 我cuda12.6,4070s cudnn-windows-x86_64-8.9.7.29_cuda12-archive.zip cuda_12.5.1_555.85_windows.…...

LLM——10个大型语言模型(LLM)常见面试题以及答案解析
今天我们来总结以下大型语言模型面试中常问的问题 1、哪种技术有助于减轻基于提示的学习中的偏见? A.微调 Fine-tuning B.数据增强 Data augmentation C.提示校准 Prompt calibration D.梯度裁剪 Gradient clipping 答案:C 提示校准包括调整提示,尽量减少产生…...

MongoDB - 聚合阶段 $count、$skip、$project
文章目录 1. $count 聚合阶段2. $skip 聚合阶段3. $project 聚合阶段1. 包含指定字段2. 排除_id字段3. 排除指定字段4. 不能同时指定包含字段和排除字段5. 排除嵌入式文档中的指定字段6. 包含嵌入式文档中的指定字段7. 添加新字段8. 重命名字段 1. $count 聚合阶段 计算匹配到…...
)
如何获取文件缩略图(C#和C++实现)
在C中,可以有以下两种办法 使用COM接口IThumbnailCache 文档链接:IThumbnailCache (thumbcache.h) - Win32 apps | Microsoft Learn 示例代码如下: VOID GetFileThumbnail(PCWSTR path) {HRESULT hr CoInitialize(nullptr);IShellItem* i…...

create-vue项目的README中文版
使用方法 要使用 create-vue 创建一个新的 Vue 项目,只需在终端中运行以下命令: npm create vuelatest[!注意] (latest 或 legacy) 不能省略,否则 npm 可能会解析到缓存中过时版本的包。 或者,如果你需要支持 IE11,你…...
Centos 7系统(最小化安装)安装Git 、git-man帮助、补全git命令-详细文章
安装之前由于是最小化安装centos7安装一些开发环境和工具包 文章使用国内阿里源 cd /etc/yum.repos.d/ && mkdir myrepo && mv * myrepo&&lscurl -O https://mirrors.aliyun.com/repo/epel-7.repo;curl -O https://mirrors.aliyun.com/repo/Centos-7…...
Golang零基础入门课_20240726 课程笔记
视频课程 最近发现越来越多的公司在用Golang了,所以精心整理了一套视频教程给大家,这个只是其中的第一部,后续还会有很多。 视频已经录制完成,完整目录截图如下: 课程目录 01 第一个Go程序.mp402 定义变量.mp403 …...

杂记-镜像
-i https://pypi.tuna.tsinghua.edu.cn/simple 清华 pip intall 出现 error: subprocess-exited-with-error 错误的解决办法———————————pip install --upgrade pip setuptools57.5.0 ————————————————————————————————————…...

如何将WordPress文章中的外链图片批量导入到本地
在使用采集软件进行内容创作时,很多文章中的图片都是远程链接,这不仅会导致前端加载速度慢,还会在微信小程序和抖音小程序中添加各种域名,造成管理上的麻烦。特别是遇到没有备案的外链,更是让人头疼。因此,…...

primetime如何合并不同modes的libs到一个lib文件
首先,用primetime 抽 timing model 的指令如下。 代码如下(示例): #抽lib时留一些margin, setup -max/hold -min set_extract_model_margin -port [get_ports -filter "!defined(clocks)"] -max 0.1 #抽lib extract_mod…...
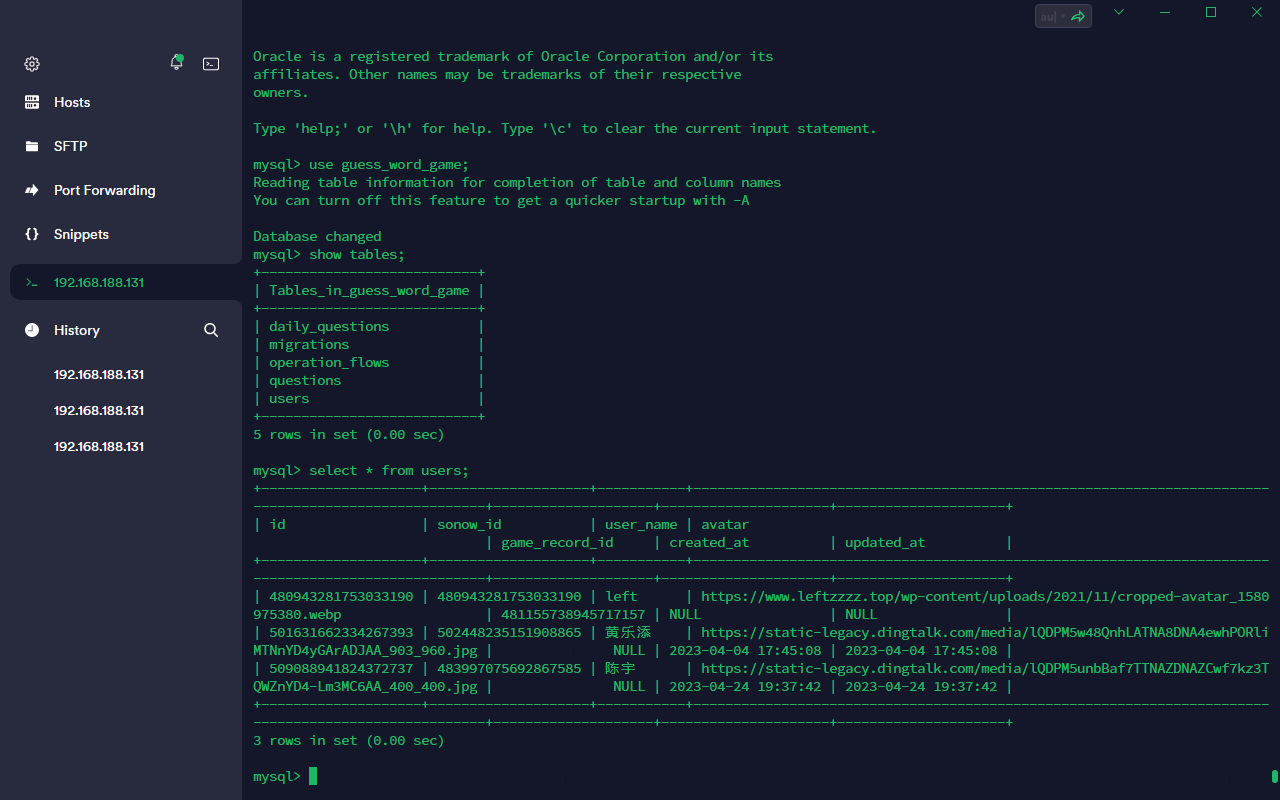
【运维笔记】数据库无法启动,数据库炸后备份恢复数据
事情起因 在做docker作业的时候,把卷映射到了宿主机原来的mysql数据库目录上,宿主机原来的mysql版本为8.0,docker容器版本为5.6,导致翻车。 具体操作 备份目录 将/var/lib/mysql备份到~/mysql_backup:cp /var/lib/…...
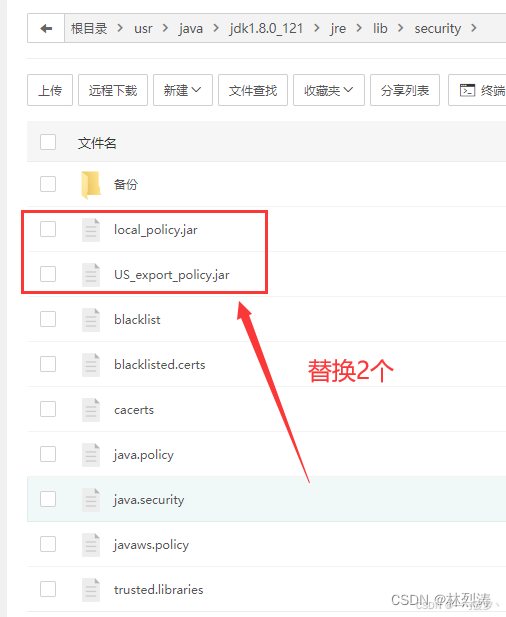
成功解决:java.security.InvalidKeyException: Illegal key size
在集成微信支付到Spring Boot项目时,可能会遇到启动报错 java.security.InvalidKeyException: Illegal key size 的问题。这是由于Java加密扩展(JCE)限制了密钥的长度。幸运的是,我们可以通过简单的替换文件来解决这个问题。 解决…...
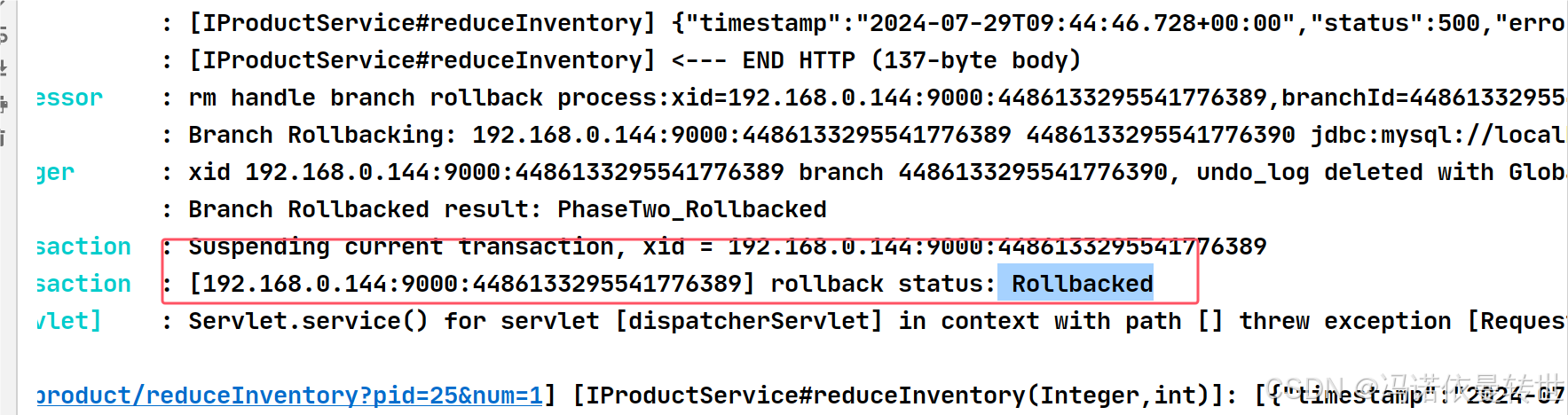
微服务事务管理(分布式事务问题 理论基础 初识Seata XA模式 AT模式 )
目录 一、分布式事务问题 1. 本地事务 2. 分布式事务 3. 演示分布式事务问题 二、理论基础 1. CAP定理 1.1 ⼀致性 1.2 可⽤性 1.3 分区容错 1.4 ⽭盾 2. BASE理论 3. 解决分布式事务的思路 三、初识Seata 1. Seata的架构 2. 部署TC服务 3. 微服务集成Se…...
—— fiddler的工作原理)
测试面试宝典(三十五)—— fiddler的工作原理
Fiddler 是一款强大的 Web 调试工具,其工作原理主要基于代理服务器的机制。 首先,当您在计算机上配置 Fiddler 为系统代理时,客户端(如浏览器)发出的所有 HTTP 和 HTTPS 请求都会被导向 Fiddler。 Fiddler 接收到这些…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
