【面试题】【C语言】寻找两个正序数组的中位数
寻找两个正序数组的中位数
仅供学习
题目

算法时间复杂度
二分查找算法,时间复杂度为 O(log(min(m, n))),其中 m 和 n 分别是两个数组的长度。
子函数
查找两个数字的最大值
int max(int a, int b) {return a > b ? a : b;
}
查找两个数字的最小值
int min(int a, int b) {return a < b ? a : b;
}
findMedianSortedArrays
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {// Ensure nums1 is the smaller arrayif (nums1Size > nums2Size) {return findMedianSortedArrays(nums2, nums2Size, nums1, nums1Size);}int x = nums1Size;int y = nums2Size;int low = 0;int high = x;while (low <= high) {int partitionX = (low + high) / 2;int partitionY = (x + y + 1) / 2 - partitionX;int maxX = (partitionX == 0) ? INT_MIN : nums1[partitionX - 1];int minX = (partitionX == x) ? INT_MAX : nums1[partitionX];int maxY = (partitionY == 0) ? INT_MIN : nums2[partitionY - 1];int minY = (partitionY == y) ? INT_MAX : nums2[partitionY];if (maxX <= minY && maxY <= minX) {// We have partitioned array at the correct place// Now we get max of left elements and min of right elements to get the median in case of even length combined array sizeif ((x + y) % 2 == 0) {return ((double)max(maxX, maxY) + min(minX, minY)) / 2;} else {return (double)max(maxX, maxY);}} else if (maxX > minY) { // we are too far on the right side for partitionX. Go on left side.high = partitionX - 1;} else { // we are too far on the left side for partitionX. Go on right side.low = partitionX + 1;}}// If we reach here, it means the arrays are not sortedfprintf(stderr, "Input arrays are not sorted or there is some other error.\n");return -1;
}
说明
- 该代码实现了一个查找两个正序数组中位数的算法,使用了二分查找法来优化时间复杂度。
- findMedianSortedArrays 函数首先确保第一个数组(nums1)是较小的一个,这样可以减小搜索范围。
- 在 while 循环中,通过二分查找确定两个数组的分割点,使得分割后的左半部分和右半部分元素数量接近。
- 根据分割点计算最大左边元素和最小右边元素,进而确定中位数。
- 主函数通过示例数据验证了算法的正确性。
相关文章:

【面试题】【C语言】寻找两个正序数组的中位数
寻找两个正序数组的中位数 仅供学习 题目 算法时间复杂度 二分查找算法,时间复杂度为 O(log(min(m, n))),其中 m 和 n 分别是两个数组的长度。 子函数 查找两个数字的最大值 int max(int a, int b) {return a > b ? a : b; }查找两个数字的最小…...

原始的原型链是怎样玩的
带着问题看代码: 1、原始的继承是怎样实现继承的? A类的prototype 属性 B类的实例 2、实现继承后,连B类的中实例的属性(放在了A类的prototype中)和原型链的上的东西都可以用 3、A.prototype.constructor实际上已经指向…...

RabbitMQ高级篇(如何保证消息的可靠性、如何确保业务的幂等性、延迟消息的概念、延迟消息的应用)
文章目录 1. 消息丢失的情况2. 生产者的可靠性2.1 生产者重连2.2 生产者确认2.3 生产者确认机制的代码实现2.4 如何看待和处理生产者的确认信息 3. 消息代理(RabbitMQ)的可靠性3.1 数据持久化3.2 LazyQueue( 3.12 版本后所有队列都是 Lazy Qu…...

正点原子imx6ull-mini-Linux驱动之platform设备驱动实验(14)
我们在前面几章编写的设备驱动都非常的简单,都是对IO进行最简单的读写操作像I2C、 SPI、LCD 等这些复杂外设的驱动就不能这么去写了,Linux 系统要考虑到驱动的可重用性,因此提出了驱动的分离与分层这样的软件思路,在这个思路下诞生…...

z3基础学习
z3基础学习 z3是一个微软出品的开源约束求解器,能够解决很多种情况下的给定部分约束条件寻求一组满足条件的解的问题。 安装:pip install z3-solver 1. 简单使用 from z3 import * x Int(x) #创建名为x的int类型变量 y Int(y) solve(x y10,2*x…...

开发助手专业版,有反编译等多种功能
软件介绍 开发助手能够用来快速调试应用以及查看手机软硬件相关信息,包括:快速打开或关闭开发者选项中的选项。 将原来几十秒的操作缩短为一次点击。包括显示布局边界,显示 GPU 过度绘制。显示布局更新。强制 GPU 渲染 显示 GPU 视图更新&a…...

嵌入式初学-C语言-十一
#接嵌入式初学-C语言-十,以及部分例题# 循环结构 break和continue break 功能: 1. 用在switch中,用来跳出switch的case语句;如果case没有break,可能会产生case穿透。 2. 用在循环中(while、do..while、for..&#…...

浅谈几个常用OJ的注册方式
众所周知,好的OJ是成功的一半,但是有些英文OJ的注册很让人伤脑筋。 CodeForces 点进官网 戳这里 然后就会进入这个页面 在这一页里面里填写好信息即可 最后,一个邮件就会发到你的邮箱上,点击其中的链接即可激活账号 AtCoder …...

Html实现全国省市区三级联动
目录 前言 1.全国省市区的Json数据 2.找到Json数据文件(在此博文绑定资源)之后,放到resource目录下。 3.通过类加载器加载资源文件,读取Json文件 3.1 创建JsonLoader类 3.2 注入JsonLoader实体,解析Json文件 4.构建前端Html页面 5.通过…...

前端构建工具Webpack 与 Vite 大对比
在现代前端开发领域,构建工具扮演着至关重要的角色。它们不仅可以帮助我们管理项目依赖关系,还可以优化我们的代码,使其在生产环境中运行得更快更高效。其中两个最受欢迎的构建工具就是 Webpack 和 Vite。在这篇文章中,我们将深入…...

Ubuntu-22.04环境搭建
安装wget(一般ubuntu会自带) sudo apt-get install wget 更换国内软件源 先备份原来的/etc/apt/source.list⽂件 sudo cp /etc/apt/sources.list /etc/apt/sources.list.bak 防止修改错误 导致无可挽回 将下列国内镜像源 写入原来的/etc/apt/source.list⽂件(注…...

嵌入式学习---DAY17:共用体与位运算
链表剩余的一些内容 一、共用体 union 共用体名 名称首字母大写 { 成员表列; }; union Demo {int i;short s;char c; }; int main(void) {union Demo d;d.i 10;d.s 100;d.c 200;printf("%d\n", sizeof(d)); /…...

蓝牙网关和蓝牙MESH总结
可参考: https://zhuanlan.zhihu.com/p/695144946 蓝牙网关 参考: https://www.bilibili.com/read/cv28872282/ 蓝牙网关是一种特殊的网络设备,它能够实现蓝牙设备与互联网或其他类型网络之间的数据传输和通信。通过蓝牙网关,用户…...

了解关于标准化的知识
1.标准化组织 1.1国家标准化管理委员会(Standardization Administration of the Peoples Republic of China,简称SAC) TC--(Technical Committee) 技术委员会. SAC/TC,就是“国家标准化管理委员会”下属的一个专项或一个行业的“技术委员会或技术小组”&a…...

【云原生】数据库忘记密码怎么办?
相信很多人都会遇到在虚拟机中忘记数据库密码的情况,想必大家都很苦恼,所以今天给大家来讲讲数据库忘记密码了如何修改密码再登录数据库!!! 1、关闭数据库服务 systemctl stop mariadb 2、执行MySQL 服务器在启动时跳…...

Postman 接口测试详解
Postman 接口测试详解 Postman 接口测试详解1. Postman 基础知识1.1 什么是 Postman?1.2 Postman 的主要功能 2. 安装与设置2.1 安装 Postman2.2 创建 Postman 账户 3. Postman 的基本操作3.1 创建和发送请求3.2 解析响应数据3.3 使用环境和变量 4. 进阶功能4.1 编写…...

【JavaEE】线程状态
目录 前言 一.线程状态图 二.线程状态 1.初始状态(NEW) 2.运行状态(RUNNING) 3.等待状态(WAITING) 4.超时等待(TIMED_WAITING) 5.阻塞状态(BLOCKED) 6.终止状态(TERMINATED) 三.线程状态间的转换 四.总结 前言 线程状态及其状态转换…...

C++笔记之编译过程和面向对象
回顾: “abcd”//数据类型 字符串常量 const char *p"abc"; new STU const char *//8 指针的内存空间 int float 指针的内存空间 p 指针指向的内存空间 "abc" 取决于字符串长度 指针变量的内容一级指针 指针变量的地址二级指针 …...

ModuleNotFoundError: No module named ‘tqdm‘
报错信息: tqdm是一个快速、可扩展的Python进度条库,用于展示迭代器的长循环执行进度。 解决:通过以下命令安装 使用conda命令安装 conda install tqdm使用pip安装: pip install tqdm...
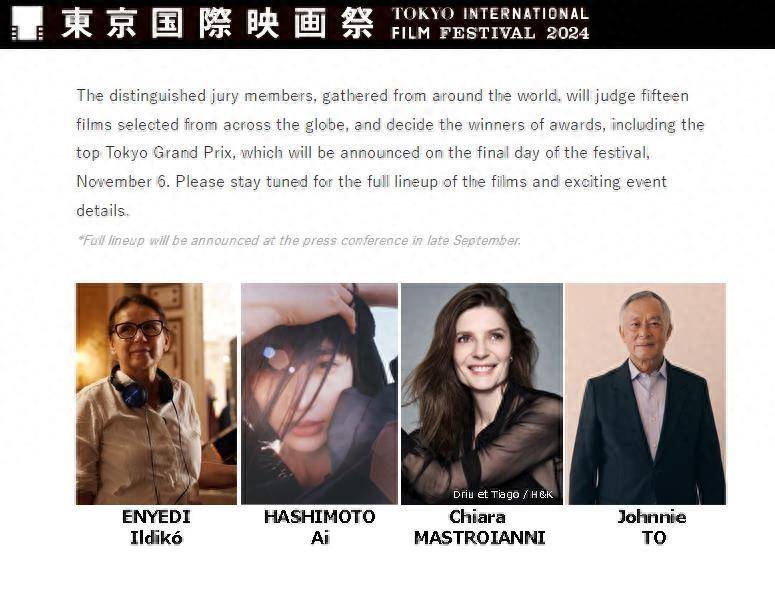
东京电影节公布2024年竞赛片评审团成员并对其业绩分别进行评介 没什么含金量
第37届东京国际电影节竞赛单元评审团名单正式公布。 周五,电影节组织者宣布,香港电影制片人杜琪峰、匈牙利电影制片人伊尔迪科恩耶迪、日本女演员桥本爱和法国女演员基娅拉马斯楚安尼将与之前宣布的评审团主席梁朝伟一起担任 2024 年主竞赛评审团成员。 …...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
