图论进阶之路-最短路(Floyd)
时间复杂度:O(n^3)
使用场景:当需要得知任意两个点的最短距离以及其路径时使用
准备:需要两个矩阵
一个记录最短距离(D)
一个记录最短路径的最后一个结点(P)
其核心在于不断的判断越过中间结点是否比不越过中间节点距离更短,迭代的结果也会影响到后面的路径的更新,通过不断的更新,使得每两个节点直接的距离被都更新到最短
具体过程:

1.初始化 D,P 矩阵,D 矩阵初始化为所有结点的入度距离,P 矩阵 初始化为所有结点的入度结点
int MAX = Integer.MAX_VALUE;int[][] D = {{MAX,MAX,MAX,MAX, 6},{ 9,MAX, 3,MAX,MAX},{ 2,MAX,MAX, 5,MAX},{MAX,MAX,MAX,MAX, 1},{MAX,MAX,MAX,MAX,MAX}};int[][] P = {{-1,-1,-1,-1, 0},{ 1,-1, 1,-1,-1},{ 2,-1,-1, 2,-1},{-1,-1,-1,-1, 3},{-1,-1,-1,-1,-1}};2.将每一个点都做一次中间结点
3.在当前中间节点的基础上,遍历所有结点,更新最短路
关于两个矩阵更新规则:
- D: 根据上一次的 D ,若 遍历到的结点到中间结点 + 中间结点到目标结点 < 上一次遍历到的结点到目标结点,就更新
- P: 若 D 发生变动,则将路径更新为 上一次 中间结点到目标节点的路径
共五个结点,故我们需要重复 5 次 2,3 步骤
public static void main(String[] args) {int MAX = Integer.MAX_VALUE/2;int[][] D = {{MAX,MAX,MAX,MAX, 6},{ 9,MAX, 3,MAX,MAX},{ 2,MAX,MAX, 5,MAX},{MAX,MAX,MAX,MAX, 1},{MAX,MAX,MAX,MAX,MAX}};int[][] P = {{-1,-1,-1,-1, 0},{ 1,-1, 1,-1,-1},{ 2,-1,-1, 2,-1},{-1,-1,-1,-1, 3},{-1,-1,-1,-1,-1}};for(int k=0;k<5;k++) {//中间结点 //遍历所有的结点对for(int i=0;i<5;i++) {for(int j=0;j<5;j++) {if(D[i][k] + D[k][j] < D[i][j]) {D[i][j] = D[i][k] + D[k][j];P[i][j] = P[k][j];}}}}}当中间点为 0 时,两个矩阵的更新结果为:
[∞, ∞, ∞, ∞, 6]
[9, ∞, 3, ∞, 15]
[2, ∞, ∞, 5, 8]
[∞, ∞, ∞, ∞, 1]
[∞, ∞, ∞, ∞, ∞]
---------------------------------
[-1, -1, -1, -1, 0]
[1, -1, 1, -1, 0]
[2, -1, -1, 2, 0]
[-1, -1, -1, -1, 3]
[-1, -1, -1, -1, -1]
=================================
当中间点为 1 时,两个矩阵的更新结果为:
[∞, ∞, ∞, ∞, 6]
[9, ∞, 3, ∞, 15]
[2, ∞, ∞, 5, 8]
[∞, ∞, ∞, ∞, 1]
[∞, ∞, ∞, ∞, ∞]
---------------------------------
[-1, -1, -1, -1, 0]
[1, -1, 1, -1, 0]
[2, -1, -1, 2, 0]
[-1, -1, -1, -1, 3]
[-1, -1, -1, -1, -1]
=================================
当中间点为 2 时,两个矩阵的更新结果为:
[∞, ∞, ∞, ∞, 6]
[5, ∞, 3, 8, 11]
[2, ∞, ∞, 5, 8]
[∞, ∞, ∞, ∞, 1]
[∞, ∞, ∞, ∞, ∞]
---------------------------------
[-1, -1, -1, -1, 0]
[2, -1, 1, 2, 0]
[2, -1, -1, 2, 0]
[-1, -1, -1, -1, 3]
[-1, -1, -1, -1, -1]
=================================
当中间点为 3 时,两个矩阵的更新结果为:
[∞, ∞, ∞, ∞, 6]
[5, ∞, 3, 8, 9]
[2, ∞, ∞, 5, 6]
[∞, ∞, ∞, ∞, 1]
[∞, ∞, ∞, ∞, ∞]
---------------------------------
[-1, -1, -1, -1, 0]
[2, -1, 1, 2, 3]
[2, -1, -1, 2, 3]
[-1, -1, -1, -1, 3]
[-1, -1, -1, -1, -1]
=================================
当中间点为 4 时,两个矩阵的更新结果为:
[∞, ∞, ∞, ∞, 6]
[5, ∞, 3, 8, 9]
[2, ∞, ∞, 5, 6]
[∞, ∞, ∞, ∞, 1]
[∞, ∞, ∞, ∞, ∞]
---------------------------------
[-1, -1, -1, -1, 0]
[2, -1, 1, 2, 3]
[2, -1, -1, 2, 3]
[-1, -1, -1, -1, 3]
[-1, -1, -1, -1, -1]
=================================
4.若最后需要得到最短路路径:可以通过 先找到 路径矩阵的位置,得到前一个点,再找到该点与前一个点的前一个点,直到前一个点变成自身为止
如:我们要找到 v1 到 v0 的最短路径
先找到 1 -> 0 的最近的前一个结点,也就是 P[1][0] = 2
得知了前一个结点为 2 ,记录路径 2 -> 0
继续往前找,1 -> 2 的前一个结点,也就是 P[1][2] = 1
得知了前一个结点为 1,记录路径 1 -> 2 -> 0
再继续往前就是寻找 1 -> 1 ,自己找自己的时候就代表路径已经完整了
故 v1 到 v0 的最短路径为: 1 -> 2 -> 0
相关文章:

图论进阶之路-最短路(Floyd)
时间复杂度:O(n^3) 使用场景:当需要得知任意两个点的最短距离以及其路径时使用 准备:需要两个矩阵 一个记录最短距离(D) 一个记录最短路径的最后一个结点(P) 其核心在于不断的判断越过中间…...

安装sqllab靶机之后,练习关卡报403 forbidden
解决办法: 在nginx的conf文件中添加上访问index.php vim /usr/local/nginx/conf/nginx.conf 保存退出 再重启一下nginx,就完成了。 ./nginx -s reload...
微信VX多开 免扫码 登录 互斥体 可视化 Exui v1.1 易语言源码附成品软件
UI设计: 1. EXUI界面库20240204 调用的模块: 1. wow64_hook_3.02.ec(压缩包内含) 2. 精易模块[v11.1.0].ec(自行下载) 更新日志: v1.1 2024年7月25日13:28:43 { 1. 有人反馈 设置了V…...

JavaEE 从入门到精通(一) ~ Maven
晚上好,愿这深深的夜色给你带来安宁,让温馨的夜晚抚平你一天的疲惫,美好的梦想在这个寂静的夜晚悄悄成长。 目录 前言 1.1 概念 什么是 Maven? Maven 的核心概念 1.2 maven依赖坐标 1.3 maven仓库 1.4 maven安装 1.5 mave…...

滚珠丝杆与丝杆支撑座:稳定性与精度的双重保障
丝杆支撑座是连接滚珠丝杆与电机的轴承,采用优质的轴承能确保支撑座与滚珠丝杆之间的刚性平衡。那么,滚珠丝杆搭连接杆支撑座有哪些优缺点呢? 正常情况下,丝杆支撑座能够提供稳定的支撑力,确保滚珠丝杆在复杂工况下保持…...

实验5-11 空心的数字金字塔
本题要求实现一个函数,输出n行空心的数字金字塔。 函数接口定义: void hollowPyramid( int n );其中n是用户传入的参数,为[1, 9]的正整数。要求函数按照如样例所示的格式打印出n行空心的数字金字塔,请注意,最后一行的…...

C#对象和类型
属性、方法、字段 字段和属性的区别 在C#中,字段(fields)和属性(properties)都是类的成员,它们提供了类存储数据的方式,但它们在用途和功能上有着明显的区别。 字段 字段通常用来存储类…...

免费分享一套SpringBoot+Vue图书(图书借阅)管理系统【论文+源码+SQL脚本】,帅呆了~~
大家好,我是java1234_小锋老师,看到一个不错的SpringBootVue图书(图书借阅)管理系统,分享下哈。 项目视频演示 【免费】SpringBootVue图书(图书借阅)管理系统 Java毕业设计_哔哩哔哩_bilibili 项目介绍 本论文阐述了一套先进的图书管理系…...

数据结构与算法--队列
文章目录 提要队列的定义队列的认识队列的应用队列的抽象数据类型队列的存储结构队列的链式存储结构与实现链队的进队和出队操作链队的数据类型初始化链队列入队操作出队操作队列的顺序存储结构与实现顺序队列的假溢出问题队列上溢循环队列循环队列取下一相邻单元下标运算队满与…...
<Qt> 常用控件
目录 一、控件概述 二、QWidget 核心属性 (一)QWidget的核心属性概览 1. enabled 2. geometry 3. WindowFrame的影响 4. windowTitle 5. window Icon 6. windowOpacity 7. cursor 8. font 9. toolTip 10. focusPolicy 11. styleSheet 三、…...
)
关于C/C++的编译、构建、CMake、x86_amd64等问题(自用)
被这些玩意整红温了 编译器版本 x86:编译器为x86版本,输出文件为x86。amd64_x86:编译器为amd64版本,输出文件为x86。amd64:编译器为amd64版本,输出文件为amd64。x86_amd64:编译器为x86版本&am…...
【设计模式】工厂模式详解
1.简介 工厂模式是一种创建型设计模式,通过提供一个接口或抽象类来创建对象,而不是直接实例化对象。工厂模式的主要思想是将对象的创建与使用分离,使得创建对象的过程更加灵活和可扩展。 工厂模式主要包括以下角色: 抽象工厂&a…...

【Spring Boot】用 Spring Security 实现后台登录及权限认证功能
用 Spring Security 实现后台登录及权限认证功能 1.引入依赖2.创建权限开放的页面3.创建需要权限验证的页面4.配置 Spring Security4.1 配置 Spring MVC4.2 配置 Spring Security 5.创建登录页面6.测试权限 1.引入依赖 使用前需要引入相关依赖,见以下代码ÿ…...

PHP开发【石头剪刀布小游戏】
石头剪刀布小游戏 玩法超级简单,你只需要在下面选择石头、剪刀或者布,然后提交,系统就会随机生成电脑的选择,告诉你最终的结果哦! 游戏规则: 如果你的选择和电脑一样,那么就是平局。如果你赢…...

(leetcode学习)42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

Python编程实例2
一、通过用户输入数字计算阶乘 # 获取用户输入的数字 num int(input("请输入一个数字: ")) factorial 1 # 查看数字是负数,0 或 正数 if num < 0:print("抱歉,负数没有阶乘") elif num 0:print("0 的阶乘为 1") e…...

排序算法:堆排序,golang实现
目录 前言 堆排序 代码示例 1. 算法包 2. 堆排序代码 3. 模拟程序 4. 运行程序 5. 从大到小排序 堆排序的思想 堆排序的实现逻辑 1. 构建最大堆 2. 排序 循环次数测试 假如 10 条数据进行排序 假如 20 条数据进行排序 假如 30 条数据进行排序 假设 5000 条数据…...

【网络安全入门】学习网络安全必须知道的77个网络基础知识
1、TCP/IP 协议的四层模型(网络接口层、网络层、传输层、应用层) TCP/IP 协议是互联网通信的基础,四层模型中,网络接口层负责与物理网络的连接;网络层主要处理 IP 数据包的路由和转发;传输层提供端到端的可…...
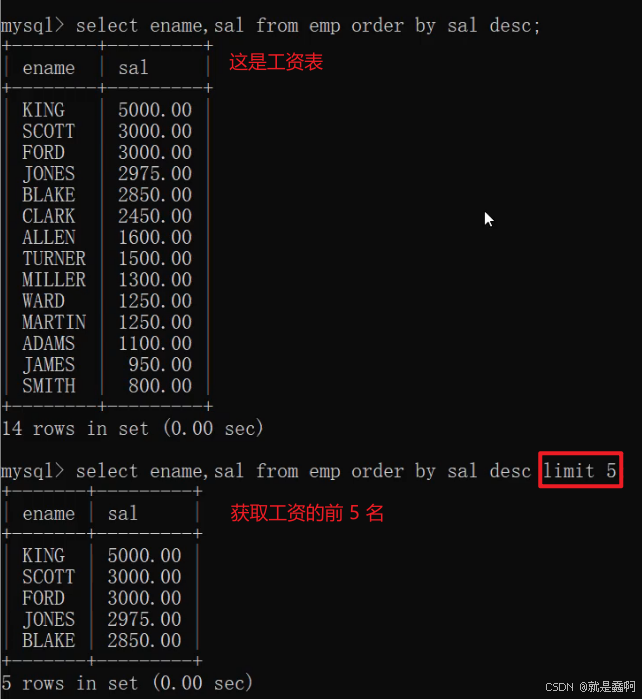
limit 以及分页 SQL 语句
目录 1. 作用 2. 演示 3. 分页 SQL 语句 1. 作用 获取结果集的一部分; 2. 演示 (1)如下,获取表的前三行; (2)只有一个数字,默认从 0 开始; (3&#x…...

mysql8.0规范
MySQL 数据库开发规范 目录 背景与目标规范列表 1. 库表设计 1.1 必须字段1.2 命名规范 2. 定义规范 2.1 约束规范2.2 类型规范 2.2.1 字段类型与长度2.2.2 状态字段数据类型2.2.3 布尔型2.2.4 varchar和text, json2.2.5 decimal(m,d) 3. 索引规范4. 其他规范5. SQL 使用 5.…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

React、Git、计网、发展趋势等内容——前端面试宝典(字节、小红书和美团)
React React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍,详细解释 用户: React Hook实现架构、.Hook不能在循环嵌套语句中使用 , 为什么,Fiber架构,面试向面试官介绍&#x…...
