Python编程实例2
一、通过用户输入数字计算阶乘
# 获取用户输入的数字
num = int(input("请输入一个数字: "))
factorial = 1
# 查看数字是负数,0 或 正数
if num < 0:print("抱歉,负数没有阶乘")
elif num == 0:print("0 的阶乘为 1")
else:for i in range(1,num + 1):factorial = factorial*iprint("%d 的阶乘为 %d" %(num,factorial))二、Python 斐波那契数列
斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13,特别指出:第0项是0,第1项是第一个1。从第三项开始,每一项都等于前两项之和。
# -*- coding: UTF-8 -*-
# Python 斐波那契数列实现
# 获取用户输入数据
nterms = int(input("你需要几项?"))
# 第一和第二项
n1 = 0
n2 = 1
count = 2
# 判断输入的值是否合法
if nterms <= 0:print("请输入一个正整数。")
elif nterms == 1:print("斐波那契数列:")print(n1)
else:print("斐波那契数列:")print(n1,",",n2,end=" , ")while count < nterms:nth = n1 + n2print(nth,end=" , ")# 更新值n1 = n2n2 = nthcount += 1三、检测用户输入的数字是否为阿姆斯特朗数
# Python 检测用户输入的数字是否为阿姆斯特朗数
# 获取用户输入的数字
num = int(input("请输入一个数字: "))
# 初始化变量 sum
sum = 0
# 指数
n = len(str(num))
# 检测
temp = num
while temp > 0:digit = temp % 10sum += digit ** ntemp //= 10相关文章:

Python编程实例2
一、通过用户输入数字计算阶乘 # 获取用户输入的数字 num int(input("请输入一个数字: ")) factorial 1 # 查看数字是负数,0 或 正数 if num < 0:print("抱歉,负数没有阶乘") elif num 0:print("0 的阶乘为 1") e…...

排序算法:堆排序,golang实现
目录 前言 堆排序 代码示例 1. 算法包 2. 堆排序代码 3. 模拟程序 4. 运行程序 5. 从大到小排序 堆排序的思想 堆排序的实现逻辑 1. 构建最大堆 2. 排序 循环次数测试 假如 10 条数据进行排序 假如 20 条数据进行排序 假如 30 条数据进行排序 假设 5000 条数据…...

【网络安全入门】学习网络安全必须知道的77个网络基础知识
1、TCP/IP 协议的四层模型(网络接口层、网络层、传输层、应用层) TCP/IP 协议是互联网通信的基础,四层模型中,网络接口层负责与物理网络的连接;网络层主要处理 IP 数据包的路由和转发;传输层提供端到端的可…...
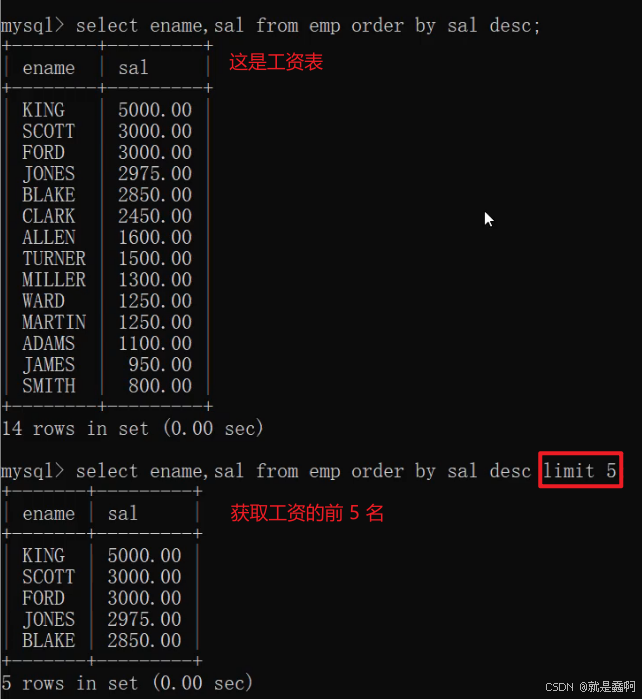
limit 以及分页 SQL 语句
目录 1. 作用 2. 演示 3. 分页 SQL 语句 1. 作用 获取结果集的一部分; 2. 演示 (1)如下,获取表的前三行; (2)只有一个数字,默认从 0 开始; (3&#x…...

mysql8.0规范
MySQL 数据库开发规范 目录 背景与目标规范列表 1. 库表设计 1.1 必须字段1.2 命名规范 2. 定义规范 2.1 约束规范2.2 类型规范 2.2.1 字段类型与长度2.2.2 状态字段数据类型2.2.3 布尔型2.2.4 varchar和text, json2.2.5 decimal(m,d) 3. 索引规范4. 其他规范5. SQL 使用 5.…...

现代前端架构介绍(第三部分):深入了解状态管理层及其对前端App的影响
远离JavaScript疲劳和框架大战,了解真正重要的东西 在第二部分中,我们讨论了功能架构的三个层次。其中一个就是状态管理层,今天我们将对其进行更深入的探讨。下面是现代前端架构系列的第三部分和最后一部分介绍。 状态管理,你可能…...
NLP与搜广推常见面试问题
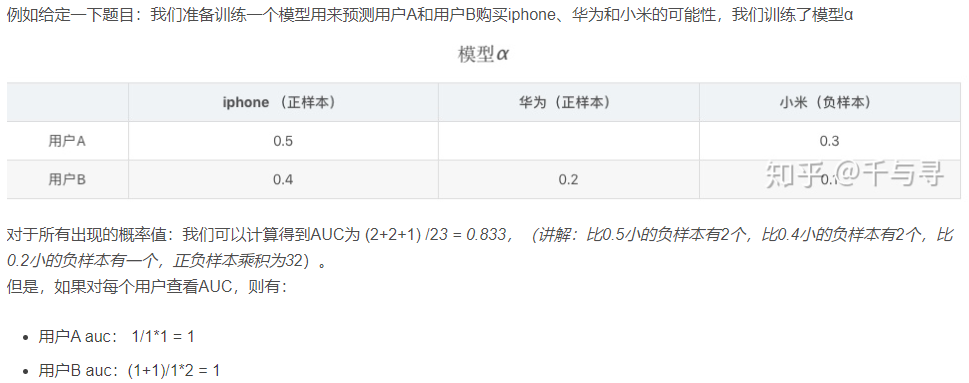
1 auc指标 AUC的两种意义 一个是ROC曲线的面积另外一个是统计意义。从统计学角度理解,AUC等于随机挑选一个正样本和负样本时,模型对正样本的预测分数大于负样本的预测分数的概率。下图为搜广推场景下的一个计算auc的例子 2 GAUC指标 就是在推荐系统…...

Python怎么实现协程并发呢?
在Python中,实现协程并发主要是通过asyncio库来完成的。asyncio是Python 3.4中引入的标准库,用于编写单线程的并发代码。使用async和await关键字,你可以定义协程和等待其他协程的完成,而不需要创建额外的线程或进程。 下面是一个使…...

专治408开始的晚!8月一定要完成这些事!
八月份才开始408,那到考试最多也只有4-5个月的时间 别担心,可以复习两轮! 其实我一直建议大家408复习三轮,但是如果时间不够,那就要在复习质量上下功夫! 考408有一个好处,就是不用先确定学校…...
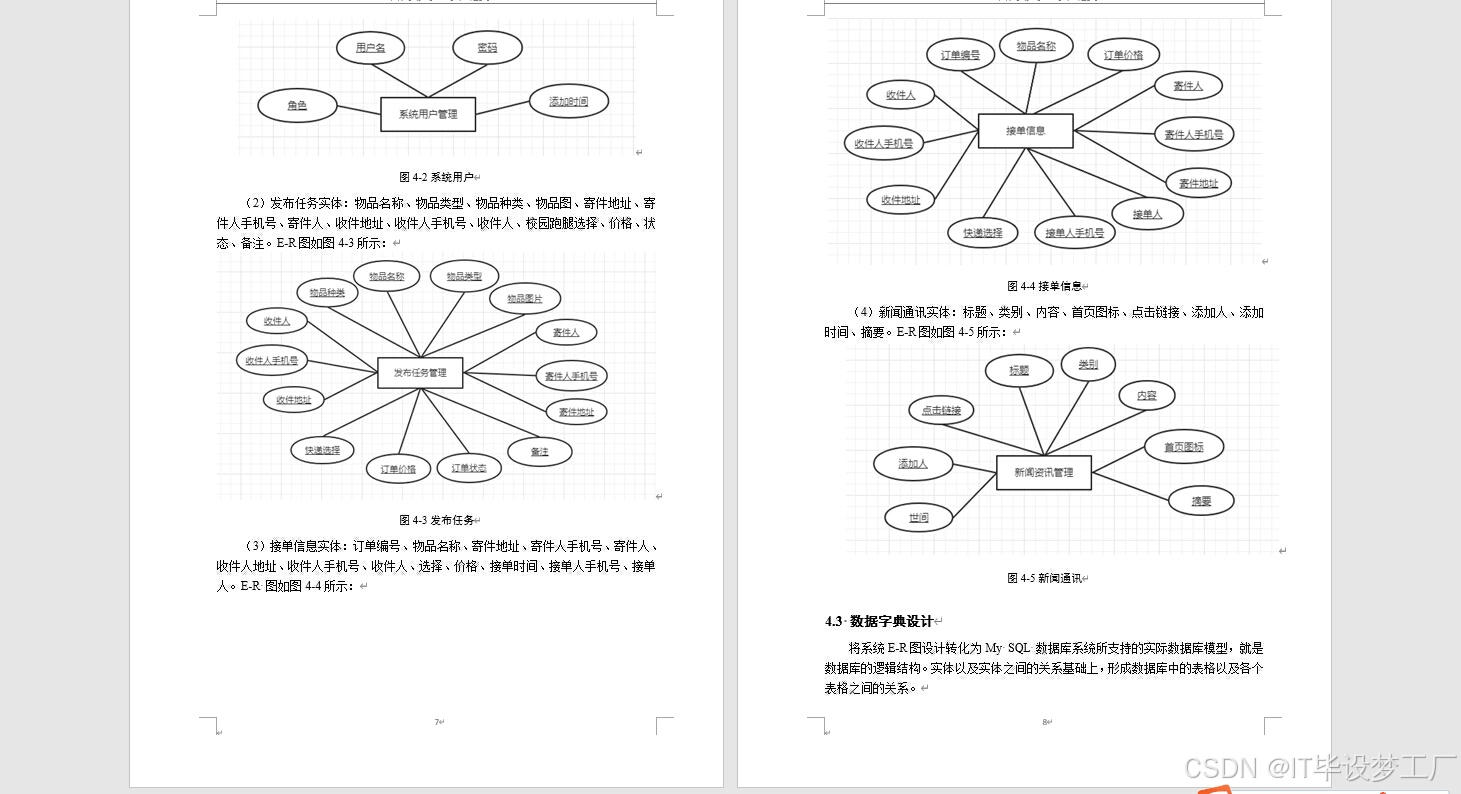
计算机毕业设计选题推荐-校内跑腿业务系统-Java/Python项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

Unity命名验证工具类
在Unity开发中,经常需要验证变量名是否符合命名规范,同时避免使用C#的保留字作为变量名。本教程将演示如何创建一个简单的工具类来实现这一功能。 步骤 1:创建Unity命名验证工具类 首先,我们创建一个C#类,命名为Unit…...
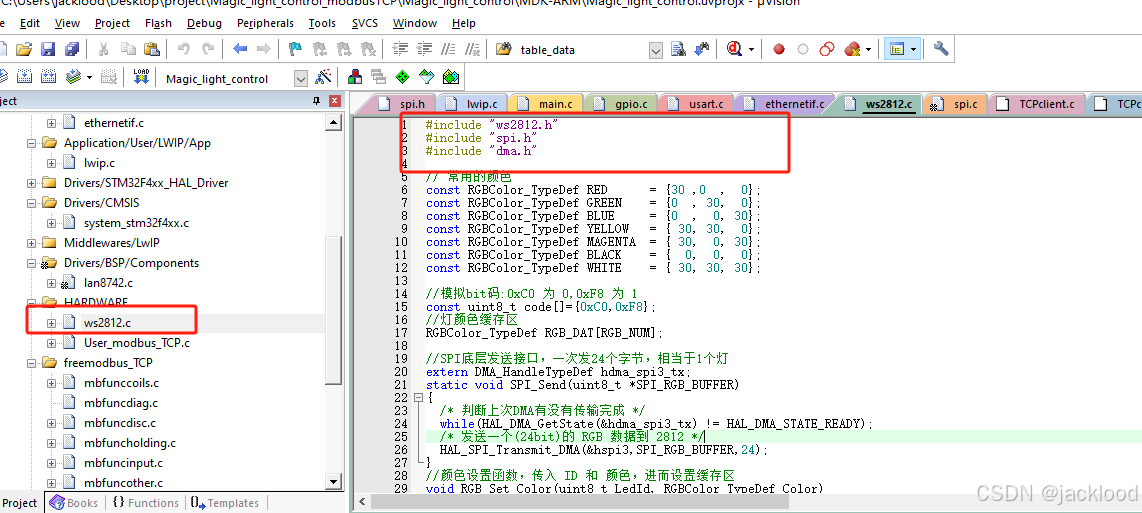
基于cubeMX的STM32开启SPI及DMA
1、打开cubeMX后,设置SPI,如下图 2、设置SPI的DMA中断 3、DMA设置 4、SPI的GPIO设置 5、最后生成代码,可以看到工程文件中有dma.c和spi.c 6、使用举例:如幻彩灯的亮灭使用SPIDMA产生的信号波形来控制,在ws2812.c中调用…...
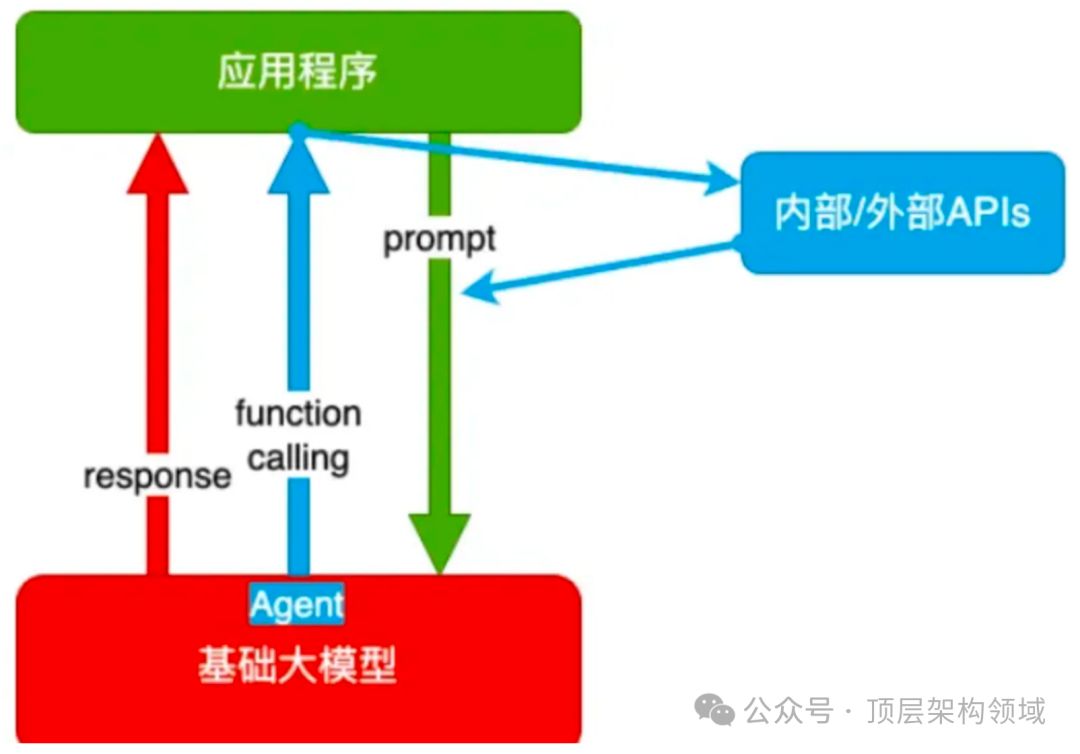
AI大模型技术的四大核心架构分析
AI大模型技术的四大核心架构演进之路 随着人工智能技术的飞速发展,大模型技术已经成为AI领域的重要分支。 深度剖析四大大模型技术架构:纯粹的Prompt提示词法、Agent Function Calling机制,RAG(检索增强生成)及Fine-…...
[C#]调用本地摄像头录制视频并保存
AForge.NET是一个基于C#框架设计的开源计算机视觉和人工智能库,专为开发者和研究者设计。它提供了丰富的图像处理和视频处理算法、机器学习和神经网络模型,具有高效、易用、稳定等特点。AForge库由多个组件模块组成,包括AForge.Imaging&#…...
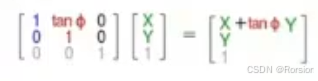
opencv-图像基础变换
1,缩放 缩放是对图像的大小进行调整 缩放矩阵,相当于x和y乘一个常数 例如将图像放大两倍 import cv2 img cv2.imread(1.jpg) img cv2.resize(img, (400,400)) img cv2.resize(img, (0,0), fx3, fy1)#表示x方向扩大三倍,y方向不变 2&…...
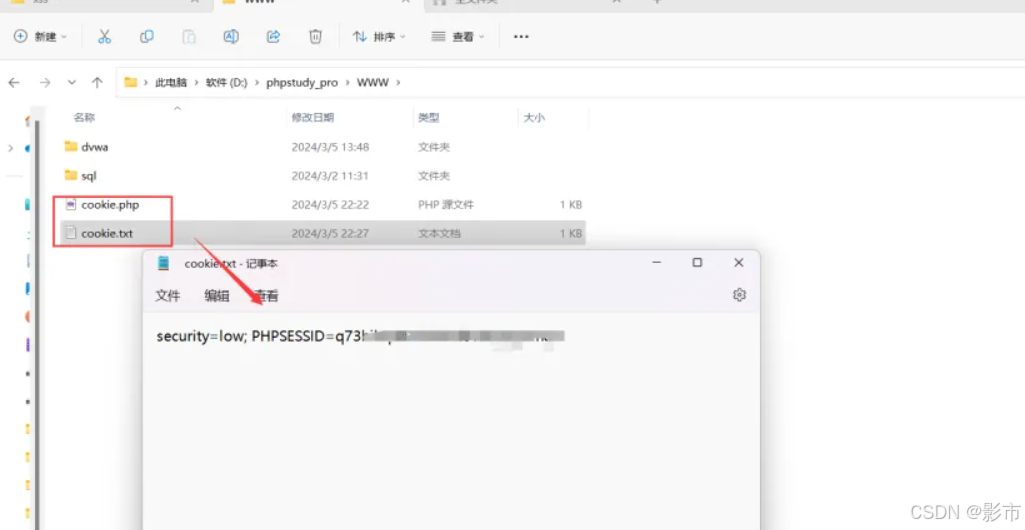
xss漏洞(三,xss进阶利用)
本文仅作为学习参考使用,本文作者对任何使用本文进行渗透攻击破坏不负任何责任。 前言: 1,本文基于dvwa靶场以及PHP study进行操作,靶场具体搭建参考上一篇: xss漏洞(二,xss靶场搭建以及简单…...
git 迁移仓库的方法
git Git是一个开源的分布式版本控制系统,由Linus Torvalds在2005年创建,用于有效、高速地处理从小到大的项目管理。它最初是为Linux内核开发而设计的,但很快被广泛用于各种项目。 以下是Git的一些主要特性: 分布式架构ÿ…...

C# Where关键字
1. 泛型约束(Generic Constraints) 在泛型类、接口或方法的定义中,where关键字用于指定类型参数的约束。这些约束可以确保类型参数具有某些特定的属性。例如它是一个类、实现了某个接口、是另一个类型的派生类、具有无参构造函数等。 1.1 …...

《计算机组成原理》(第3版)第1章 计算机系统概论 复习笔记
第1章 计算机系统概论 一、计算机系统简介 (一)计算机的软硬件概念 1.计算机系统由“硬件”和“软件”两大部分组成 (1)所谓“硬件”,是指计算机的实体部分,如主机、外部设备等。 ࿰…...

达梦数据库的系统视图v$cachers
达梦数据库的系统视图v$cachers 达梦数据库的系统视图V$CACHERS的作用是显示缓存中的项信息,在 ini 参数 USE_PLN_POOL !0 时才统计。这个视图帮助数据库管理员监控和分析缓存的使用情况,优化数据库性能。通过查询V$CACHERS视图,可以获取缓存…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
