【Linux】sersync 实时同步
原理
rsync 是不支持实时同步的,通常我们借助于 inotify 这个软件来实时监控文件变化,一旦inotify 监控到文件变化,则立即调用 rsync 进行同步,推送到 rsync 服务端。
环境准备
步骤1:获取数据包
获取 sersync 的包安装到存储服务器-nfs01上,这里我是用博客园-刘应杰的提供的链接 wget 获取的包进行测试。
sersync下载安装及配置(有演示示例) - 刘应杰 - 博客园 (cnblogs.com)
wget http://down.whsir.com/downloads/sersync2.5.4_64bit_binary_stable_final.tar.gz目录规划:/app/tools/sersync//app/tools/sersync/bin//app/tools/sersync/conf/
修改之前:GNU-Linux-x86/GNU-Linux-x86/sersync2GNU-Linux-x86/confxml.xml
修改完成后样子:[root@nfs01 /app/tools/sersync]# tree
.├── bin│ └── sersync└── conf└── confxml.xml步骤2:创建目录
mkdir -p /app/tools/sersync/{bin,conf}步骤3:迁移配置目录
mv GNU-Linux-x86/sersync2 /app/tools/sersync/bin/mv GNU-Linux-x86/confxml.xml /app/tools/sersync/conf/步骤4:查看结果
tree -F /app/tools/完整演示
实验设备
- 存储服务器:172.16.1.31
- web服务器:172.16.1.7
- 备份服务器:172.16.1.41
操作流程
步骤1:备份服务器:修改的rsyncd配置文件,添加准备实时同步的共享目录
vim /etc/rsyncd.conf# 在配置文件中添加如下信息
[nfsbackup]
comment = realtime
path=/nfsbackup步骤2:备份服务器:创建共享目录修改权限
mkdir -p /nfsbackupchown -R rsync.rsync /nfsbackup/步骤3:备份服务器:重启 rsync
systemctl restart rsyncd步骤3:存储服务器:修改 sersync 的 confxml.xml 配置文件
具体修改如下:左修改后,有原文件

步骤4:存储服务器:创建软连接
ln -s /app/tools//sersync/bin/sersync2 /bin/步骤5:存储服务器:启动或者关闭服务
# 启动
sersync2 -rdo /app/tools/sersync/conf/confxml.xml# 关闭两种选择
# 第一种
pkill sersync2# 第二种
kill 进程id步骤6:存储服务器:配置文件 /etc/exports
vim /etc/exports# 添加配置
/data/ 172.16.1.0/24(rw)相关文章:

【Linux】sersync 实时同步
原理 rsync 是不支持实时同步的,通常我们借助于 inotify 这个软件来实时监控文件变化,一旦inotify 监控到文件变化,则立即调用 rsync 进行同步,推送到 rsync 服务端。 环境准备 步骤1:获取数据包 获取 sersync 的包…...

Unity 资源分享 之 恐龙Ceratosaurus资源模型携 82 个动画来袭
Unity 资源分享 之 恐龙Ceratosaurus资源模型携 82 个动画来袭 一、前言二,资源包内容三、免费获取资源包 一、前言 亲爱的 Unity 开发者和爱好者们,大家好!今天要为大家分享一份超级酷炫的 Unity 资源——恐龙资源模型,而且它还…...

【AI绘画】 学习内容简介
AI绘画-学习内容简介 1. 效果展示 本次测试主要结果展示如下: 卡通手办定制1 卡通手办定制2 艺术写真定制 2. 主要目录 AI 绘画- 文生图,图生图及lora使用(基于diffusers) AI 绘画- 模型转换与快速生图(基于diffus…...

树形结构查找(B树、B+树)
平衡树结构的树高为 O(logn) ,平衡树结构包括两种平衡二叉树结构(分别为 AVL 树和 RBT)以及一种树结构(B-Tree,又称 B 树,它的度大于 2 )。AVL 树和 RBT 适合内部存储的应用,而 B 树…...

网络通信(TCP/UDP协议 三次握手四次挥手 )
三、TCP协议与UDP协议 1、TCP/IP、TCP、 UDP是什么 TCP/IP协议是一个协议簇,里面包括很多协议的, UDP只是其中的一个, 之所以命名为TCP/IP协议, 因为TCP、 IP协议是两个很重要的协议,就用他两命名了,而TCP…...

C# ADO.Net 通用按月建表插入数据
原理是获取原表表结构以及索引动态拼接建表SQL,如果月表存在则不创建,不存在则创建表结构 代码如下 /// <summary>/// 根据指定的表名和时间按月进行建表插入(如果不存在对应的月表)/// </summary>/// <param nam…...

19-ESP32-C3加大固件储存区
1默认编译情况。 2、改flash4M。ESP-IDF Partition Table Editor修改。 3、设置输入Partition Table 改自定义.CSV。保存。 4、查看命令输入Partition Table Editor打开-分区表编辑器UI。按图片增加。 nvs,data,nvs,0x9000,0x6000,, phy_init,data,phy,0xF000,0x1000,, factory…...

【STL】stack/queue 容器适配器 deque
1.stack的介绍和使用 1.1.stack的介绍 1. stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,其删除只能从容器的一端进行元素的插入与提取操作。 2. stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其底层的容…...

(回溯) LeetCode 17. 电话号码的组合
原题链接 一. 题目描述 17. 电话号码的字母组合 已解答 中等 相关标签 相关企业 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对…...

Ghidra:开源软件逆向工程框架
Ghidra 是一个软件逆向工程 (SRE) 框架 Ghidra 是一种尖端的开源软件逆向工程 (SRE) 框架,是美国国家安全局 (NSA) 研究局的产品。 Ghidra 该框架具有高端软件分析工具,使用户能够分析跨各种平台(包括 Windows、macOS 和 Linux)…...
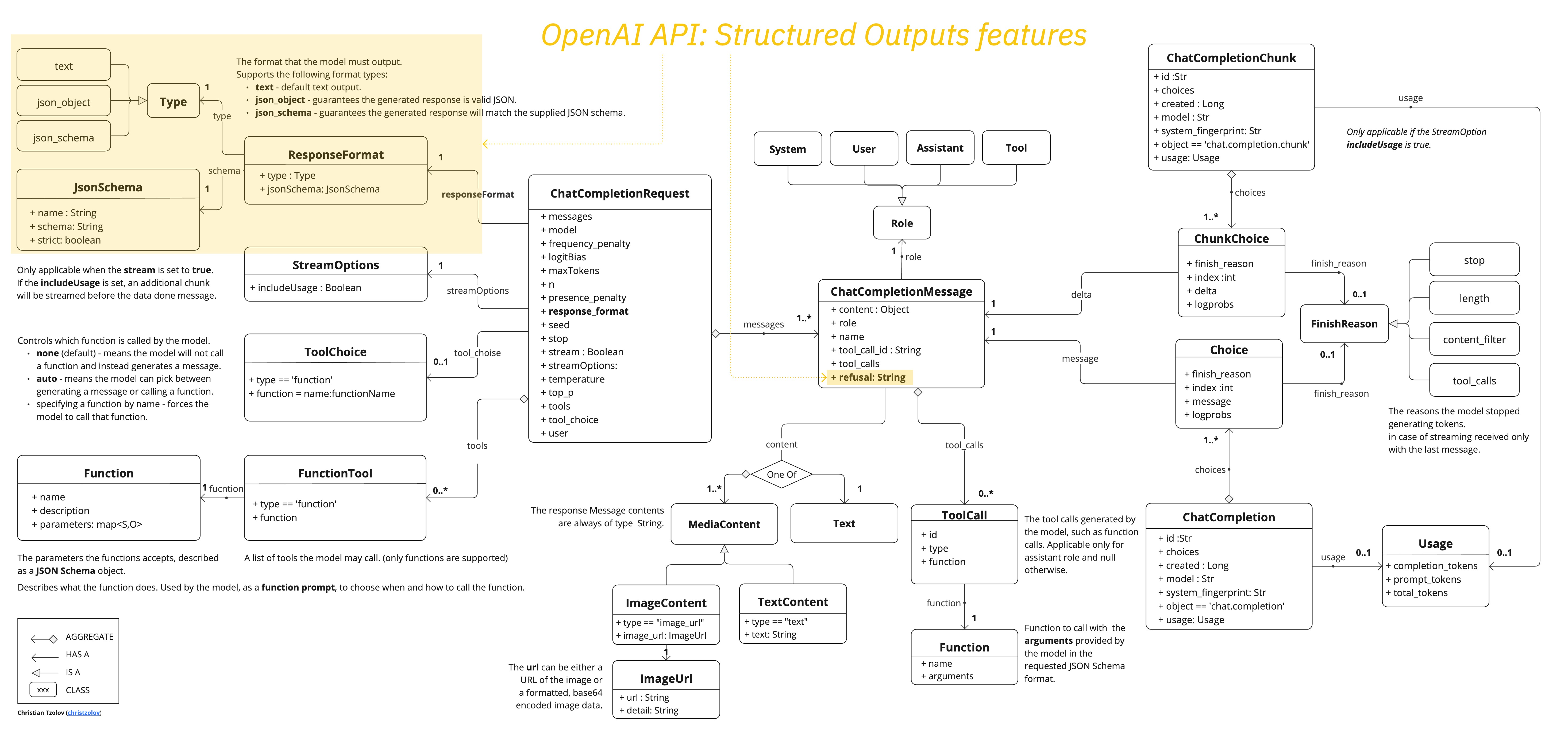
Spring AI 更新:支持OpenAI的结构化输出,增强对JSON响应的支持
就在昨晚,Spring AI发了个比较重要的更新。由于最近OpenAI推出了结构化输出的功能,可确保 AI 生成的响应严格遵守预定义的 JSON 模式。此功能显着提高了人工智能生成内容在现实应用中的可靠性和可用性。Spring AI 紧随其后,现在也可以对OpenA…...

java.util.ConcurrentModificationException 并发修改异常
目录 异常代码片段 详细说明 解决方案 使用迭代器进行遍历 使用临时集合存储结果 异常代码片段 if (ObjectUtil.isNotEmpty(candidateUsers)) {candidateUsers candidateUsers.stream().filter(Objects::nonNull).distinct().collect(Collectors.toList());for (String …...
)
Flask数据库操作(第四阶段)
目录 Flask数据库操作一、数据库基础1.1 关系型数据库与非关系型数据库选择数据库 二、Flask-SQLAlchemy2.1 安装 Flask-SQLAlchemy2.2 创建数据库模型2.2.1 创建 Flask 应用2.2.2 定义模型 2.3 执行 CRUD 操作2.3.1 创建(Create)2.3.2 读取(…...

C语言问答进阶--5、基本表达式和基本语句
赋值表达式 表达式是什么?表达式是由运算符和操作数组成的式子。 如下的代码 #include "iostream.h" int main() { int a1,b2,sum; cout<<(sumab)<<endl; return 0; } 那么如下的呢? #include "iostream.h" int mai…...

uniapp3.0实现图片上传公用组件上传uni-file-picker,uni.uploadFile
用uniapp3.0的写法组合式api,setup形式封装一个图片上传公用组件,要求 1、使用uni-file-picker选择文件 2、uni.uploadFile上传图片 3、要能支持上传接口动态化 4、支持删除如片列表中已上传项 5、可以预览已上传列表图片 6、支持动态化限制图片格…...

Unity游戏开发002
Unity游戏开发002 目录 第一章:Hello,Unity!第二章:创建一个游戏体 本文目录 Unity游戏开发 Unity游戏开发002目录本文目录前言一、创建一个游戏体1. 编辑器语言设置2. 创建游戏对象的两种方法3. 快速复制和粘贴物体4. 注意事项…...

MySQL基础练习题38-每位教师所教授的科目种类的数量
目录 题目 准备数据 分析数据 总结 题目 查询每位老师在大学里教授的科目种类的数量。 准备数据 ## 创建库 create database db; use db;## 创建表 Create table If Not Exists Teacher (teacher_id int, subject_id int, dept_id int)## 向表中插入数据 Truncate table…...

haproxy 原理+实战
haproxy 1 haproxy简介1.1 定义1.2 原理讲解1.3 HAProxy的优点: 2. haproxy的基本部署2.1 实验环境2.1.2 haproxy主机配置2.1.3 webserver1配置2.1.4 webserver2配置 3. haproxy的全局配置4. haproxy代理参数5. haporxy的热处理6.haproxy的算法6.1 静态算法6.1.1sta…...

OSPF进阶
一、LSA详解 Type:LSA的类型(1、2、3、4、5、7类) link-state-ID:链路状态表示符 ADV router:产生该LSA的路由器 age:老化时间 Metric:开销值,一般都为ADV router到达该路由的开…...
SuccBI+低代码文档中心 — 可视化分析(仪表板)(下)
制作仪表板 引入数据模型 仪表板所需模型已经在数据模块中准备好,可以将对应模型表添加到数据模型中。提供了两种添加方式: 在数据栏中点击添加按钮,在弹出框中通过搜索或直接在其所在目录下选中该模型,点击确定。 点击数据按钮…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
