【C++ 第十五章】map 和 set 的封装(封装红黑树)
1. map 和 set 的介绍
⭐map 与 set 分别是STL中的两种序列式容器;
它们是一种树形数据结构的容器,且其的底层构造为一棵红黑树;
而在上一篇文章中提到,其实红黑树本身就是一棵二叉搜索树,是基于二叉搜索树的性质对其增加了平衡的属性来提高其综合性能
⭐当然也提到了红黑树与AVL树的区别:
1、AVL树保证了严格的平衡,其树高不会很高,使其查找效率较高,但是就是因为要不断旋转保证平衡,因此 当插入和删除时,较多的旋转会影响效率
2、红黑树不用保证严格的平衡,查找的时间复杂度为 O(logN) 级别(和AVL树)在 插入和删除 中,只需要较少的旋转,因此 插入和删除 效率较高
综合考虑 map 和 set 使用 红黑树作为底层容器
2. map 和 set 的结构
在 map 与 set 的使用过程中,由于 set 容器的底层树节点存储着数据为 key (T 类型)
而 map 的底层树节点存储着数据为一个键值对 key/value; (pair类型)
所以可能会联想到在STL中的这两个容器是否使用的是不同的红黑树?
而实际在 STL 的源码中可以看到,对于这两个容器而言所使用的是同一个红黑树(即调用同一棵红黑树),并且利用泛型的特性来控制两个容器中所使用的对应的参数;
那么既然是同一棵红黑树,应该如何对这棵树进行修改 使得该树能够同时兼容 map 的 key/value 键值对数据存储 和 set 的 key 数据存储 呢?
3、对红黑树的进一步修改
在我们的上一章节 讲解了红黑树的各种基础构造,本章对红黑树进一步修改,融入 迭代器 以及 泛型化使其更加适配 map 与 set
(1)修改一:将节点数据类型换成 T (泛型的思想)
将节点中数据变量 换成 类型T
当 T == key 类型时,该节点对应 set 容器
当 T == pair<key, value> 类型时,该节点对应 map 容器
这样就初步实现,同一节点类模板,可以对应 多种数据类型,适应 set 和 map
template<class T> struct RBTreeNode {T _data; // 泛型化思想:_data 可以是 Key 类型,也可以是 pair<Key, Value> 类型// ..... };
先前 set 和 map 要设计两套 红黑树类
为了适应 set:
template<class Key>
class RBTree
{}为了适应 map:
template<class Key, class Value>
class RBTree
{}现在节点类泛型化了,红黑树类也要对应修改
template<class T>
class RBTree
{}(2)修改二:应用仿函数 修改 插入函数 insert 内部比较逻辑
⭐之前没修改时,为了适应 set 和 map ,要设计两种传参类型
为了适应 set:
bool insert(const K& key) {}为了适应 map:
bool insert(const pair<K, V>& kv) {}
⭐insert 函数内部比较键值大小的部分 也有两套设计
当 T == key 时,对应 set,insert 函数内部比较键值大小的部分:直接比较键值 key
if (cur->_key < key) {// ..... }当 T == key/value 时,对应 map,insert 函数内部比较键值大小的部分:还要指定键值对的 first
if (cur->_kv.first < kv.first) {// ..... }
现在 节点数据泛型为 T,函数 insert 传参类型和内部某些比较逻辑都需要做调整
⭐ 修改传参类型
bool insert(const T& data)
{}⭐内部某些比较逻辑:使用仿函数
因为我们那里的就是要用 键值 key 比较,因此 set 可以直接用节点数据 key 比较,而 map 需要用 节点数据pair的first 比较,这里就有区别,因此需要仿函数“统一化”
(1)set :
使用仿函数时,当操作数类型为 K 类型,则直接识别使用 set 的仿函数 set_KeyOfT 中的 operator() 函数,返回 key(即返回一个键值)
template<class K>
class set
{// set 中的仿函数struct set_KeyOfT {const K& operator()(const K& key) {return key;}};// ....... 其他补充
private:RBTree<K, set_KeyOfT> _tree;
};(2)map
当操作数类型为 pair<key, value> 键值对类型,则直接识别为 map 的仿函数 map_KeyOfT 中的 operator() 函数,返回 pair<key, value> 的 first (即也返回一个 键值)
template<class K, class V>
class map
{struct map_KeyOfT {const K& operator()(const pair<K, V>& kv) {return kv.first;}};// ....... 其他补充private:RBTree<pair<const K, V>, map_KeyOfT> _tree;
};在 红黑树类模板中添加 仿函数的类型:class KeyOfT
template<class T, class KeyOfT>
class RBTree
{}仿函数的应用
KeyOfT kot; // 创建一个仿函数类对象
if (kot(cur->_data) < kot(data)) // data 可能是 key类型,可能是 pair<key, value> 类型
// 使用仿函数,调用operator() 自动识别 data 的类型,放回 键值 key 进行比较(3)修改三:给 红黑树类模板 再加一个 类型 class K
我们实现 find 和 insert 函数时,insert 函数参数类型是 T ,表示 data 可以是 key 类型,也可以是 pair< key, value > 类型
但是 find 函数参数可以是 T 类型吗??
不可以!,无论是 map or set,find 函数都是查找 键值 key,固定要用 key
若 find 的参数是 T 类型,当 T == key 时,直接可以使用,当 T == pair< key, value > 时,就不能直接使用 T 来查找,就要使用 T.first,就使得两个类型造就两种使用逻辑
因此 我们可以额外传一个 键值(既然是固定要用的,就多传一个)
template<class K, class T, class KeyOfT>
class RBTree
{}
至此,我们红黑树类模板中 第一个参数 K 用于传键值key,第二个参数 T 为泛型用于 接收两种类型(兼容set 和 map 两种),第三个参数为 仿函数
(4)修改四:插入函数 insert 的 返回值 改为 pair 类型
在STL中,无论是 map 容器还是 set 容器,其插入函数Insert()函数的返回值都是为一个pair<iterator,bool>;
1、若是插入成功则返回新插入节点的迭代器位置 与 true; (迭代器的实现将在下文中提到)
2、若是插入失败则返回与需要插入的数据相同的节点位置 与 false;
例如 STL 库中的 map 的 insert 函数源码
pair<iterator,bool> insert (const value_type& val);value_type 就是 pair< K, V>
pair 是一个类模板
我们的 插入函数 返回值修改为:
pair<iterator, bool> insert(const T& data)4. 迭代器
因为需要将 红黑树封装进容器 map 和 set 中,容器会涉及各种操作,需要迭代器
因此我们先实现 红黑树的迭代器
因为 map 和 set 的底层是 红黑树,因此 他们的 迭代器就是将一个树节点指针封装成一个类
1.1 基础类框架和函数
基础函数:重载点操作符、重载箭头操作符、重载不等于操作符、构造函数
template<class T, class Ref, class Ptr> struct RBTreeIterator {typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;Node* _p;Ref operator*() {return _p->_data;}Ptr operator->() {return &(_p->_data);}// 两个迭代器比较相等 就是直接比较 两个指针bool operator!=(const Self& x) {return _p != x._p;}RBTreeIterator(Node* p):_p(p){} };
1.2 重载前置++ 和 前置--
关于前置++
在 二叉搜索树中 前置++,需要使迭代器指向 中序遍历的 下一个位置
因此,设计前置++ 就需要模拟中序遍历找到下一个节点

中序遍历顺序是:左孩子 ---> 根 ---> 右孩子
若当前节点为 节点 5,按照中序,下一个位置是 节点 7,即 根节点(从左孩子到根节点)
若当前节点为 节点 7,按照中序,下一个位置是 节点 9,即 右孩子(从根节点到右孩子)
若当前节点为 节点 9,按照中序,右孩子为 空,证明已经走完一个中序(左根右),应该回溯到 祖先节点,寻找 当前节点为 父亲的左孩子的关系,即 从节点9 一直到 节点 7,此时 节点7 是父亲节点 11 的左孩子(这样满足 从左孩子到根节点 ,即节点 9 的下一个位置就是 节点 11)
若当前节点为 节点 11,按照中序,下一个位置是 节点 12,即右子树的 最左节点(在右子树,循环向下找到右子树的最左节点)
综合上面几种情况,可以得出以下逻辑
1、右不为空,则 自己就是 根:右子树最左节点就是中序下一个,while() 循环 找 右子树的 最左节点
2、右为空,则 cur 和 parent 沿着到根节点的路径向上查找,直到 孩子 cur 是父亲 parent 的 left
此时 parent 就是中序的下一个节点
伪代码:
定义 cur = 当前位置
if(cur 的 右不为空)
循环找右子树的最左节点
else if(cur 的 右为空)
定义 parent
while(parent 不为 空 且 parent 的左 不为 cur)
循环结束,parent 就是 中序的写一个节点
实际代码:
Self& operator++() {Node* cur = _p;if (cur->_right) {cur = cur->_right;while (cur->_left) { // 注意这里是 cur->_left 我们目的是到最左节点,不是 空节点!cur = cur->_left;}}else {Node* parent = cur->_parent;while (parent && parent->_left != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this; }
关于前置--
重载前置-- 也 同理,就是倒着中序遍历(右 根 左)
注意:前置-- 的第一个节点可能为 end(),本文中我们将 end() 设置为 最后一个节点的下一个节点,即为 NULL
当对 end() == NULL 前置-- 时,可能导致空指针访问的错误,因此需要特殊处理
end() 的前一个即为 二叉树的 最后一个节点(中序遍历的最后一个:右子树的最右节点)
Node* cur = _p; // 如果 cur 为 nullptr 代表现在指向 end() // 特殊处理 if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur; }
前置-- 的代码:
// 减减 和 加加的 逻辑刚好相反 Self& operator--() {Node* cur = _p;// 如果 cur 为 nullptr 代表现在指向 end()// 特殊处理if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur;}// 下面的逻辑和 前置++ 差不多:镜像反转理解即可else if (cur->_left) {cur = cur->_left;while (cur->_right) {cur = cur->_right;}}else {Node* parent = cur->_parent;while (parent && parent->_right != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this; }
1.3 将 迭代器封装进 红黑树
这里定义了:begin() / end() (且为 iterator 和 const_iterator 两个版本)
此处:红黑树的 begin 是整棵二叉搜索树的 最左边的节点(即中序遍历的第一个节点),因此需要循环操作
template<class K, class T, class KeyOfT> class RBTree { public:typedef RBTreeNode<T> Node;// 定义迭代器typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T, const T&, const T*> const_iterator;// 迭代器iterator begin() {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return iterator(cur, _root);}iterator end() {return iterator(nullptr, _root);}const_iterator begin() const {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return const_iterator(cur, _root);}const_iterator end() const {return const_iterator(nullptr, _root);}private:Node* _root = nullptr; };
就是上面这一部分封装了迭代器,其他的红黑树代码部分上一章都实现了,这里暂不赘述
1.4 ⭐ 迭代器类 完整代码
注释都有解释了,若不明白,可以评论区讨论或私信
// T :节点中的数据类型
// Ref:引用类型 T& 或 const T&
// Ptr:指针类型 T* 或 const T*
template<class T, class Ref , class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node; // 重定义节点类命名typedef RBTreeIterator<T, Ref, Ptr> Self; // 对自己的迭代器类型重命名Node* _p; // 迭代器中指向节点的指针Ref operator*() {return _p->_data;}Ptr operator->() {return &(_p->_data);}// 两个迭代器比较相等 就是直接比较 两个指针bool operator!=(const Self& x) {return _p != x._p;}bool operator==(const Self& x) const {return _p == x._p;}// 我写的函数 cur 有点冗余,其实代码可以更加精简Self& operator++() {Node* cur = _p;if (cur->_right) {cur = cur->_right;while (cur->_left) { // 注意这里是 cur->_left 我们目的是到最左节点,不是 空节点!cur = cur->_left;}}else {Node* parent = cur->_parent;while (parent && parent->_left != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}// 减减 和 加加的 逻辑刚好相反Self& operator--() {Node* cur = _p;// 如果 cur 为 nullptr 代表现在指向 end()// 特殊处理if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur;}// 下面的逻辑和 前置++ 差不多:镜像反转理解即可else if (cur->_left) {cur = cur->_left;while (cur->_right) {cur = cur->_right;}}else {Node* parent = cur->_parent;while (parent && parent->_right != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}RBTreeIterator(Node* p, Node* root):_p(p){}
};5. ⭐红黑树 完全体(含迭代器+适配 map 和 set 的泛型)
含有
红黑树节点类
迭代器类
红黑树类:拷贝构造、赋值运算符重载、析构、插入函数、4种旋转函数、查找 find、中序遍历、求树的高度、求树的节点个数、判断树是否平衡
#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;// 设置颜色枚举值
enum Colour {RED,BLACK
};template<class T>
struct RBTreeNode
{typedef RBTreeNode<T> Node;T _data; // 泛型化思想:_data 可以是 Key 类型,也可以是 pair<Key, Value> 类型Node* _left;Node* _right;Node* _parent;Colour _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr){}
};// T :节点中的数据类型
// Ref:引用类型 T& 或 const T&
// Ptr:指针类型 T* 或 const T*
template<class T, class Ref , class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node; // 重定义节点类命名typedef RBTreeIterator<T, Ref, Ptr> Self; // 对自己的迭代器类型重命名Node* _p; // 迭代器中指向节点的指针Node* _root; Ref operator*() {return _p->_data;}Ptr operator->() {return &(_p->_data);}// 两个迭代器比较相等 就是直接比较 两个指针bool operator!=(const Self& x) {return _p != x._p;}bool operator==(const Self& x) const {return _p == x._p;}// 我写的函数 cur 有点冗余,其实代码可以更加精简Self& operator++() {Node* cur = _p;if (cur->_right) {cur = cur->_right;while (cur->_left) { // 注意这里是 cur->_left 我们目的是到最左节点,不是 空节点!cur = cur->_left;}}else {Node* parent = cur->_parent;while (parent && parent->_left != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}// 减减 和 加加的 逻辑刚好相反Self& operator--() {Node* cur = _p;// 如果 cur 为 nullptr 代表现在指向 end()// 特殊处理if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur;}// 下面的逻辑和 前置++ 差不多:镜像反转理解即可else if (cur->_left) {cur = cur->_left;while (cur->_right) {cur = cur->_right;}}else {Node* parent = cur->_parent;while (parent && parent->_right != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}RBTreeIterator(Node* p, Node* root):_p(p),_root(root){}
};template<class K, class T, class KeyOfT>
class RBTree
{
public:typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T, const T&, const T*> const_iterator;RBTree() = default;~RBTree() {destory(_root);_root = nullptr;}// 拷贝构造RBTree(const RBTree<K, T, KeyOfT>& t) {_root = CopyTree(t._root);}// 赋值重载RBTree<K, T, KeyOfT>& operator=(const RBTree<K, T, KeyOfT>& t) {RBTree tmp(t);std::swap(_root, tmp._root);return *this;}// 迭代器iterator begin() {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return iterator(cur, _root);}iterator end() {return iterator(nullptr, _root);}const_iterator begin() const {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return const_iterator(cur, _root);}const_iterator end() const {return const_iterator(nullptr, _root);}// 查找iterator find(const K& key) const {Node* cur = _root;while (cur) {if ((cur->_data).first < key) {cur = cur->_right;}else if ((cur->_data).first > key) {cur = cur->_left;}else return iterator(cur, _root);}return end();}// 插入// 插入成功就是 true,迭代器指向新插入的节点// 插入失败就是 false,迭代器指向已存在的那个节点pair<iterator, bool> insert(const T& data) {if (_root == nullptr) {_root = new Node(data);_root->_col = BLACK; // 根节点一定是黑的return make_pair(iterator(_root, _root), true);}// 利用仿函数KeyOfT kot;Node* cur = _root;Node* parent = cur;while (cur) {if (kot(cur->_data) < kot(data)) {parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)) {parent = cur;cur = cur->_left;}else return make_pair(iterator(cur, _root), false);}// 在 cur 的位置插入该节点cur = new Node(data);cur->_col = RED; // 新增节点给 红的Node* newNode = cur; // 这里记录以下初始的 cur,避免下面各种操作改变 cur// 父连子,子连父if (kot(parent->_data) > kot(data)) parent->_left = cur;else parent->_right = cur;cur->_parent = parent;// 变色调整:while (parent && parent->_col == RED) {Node* Grandfather = parent->_parent;/*gp u*/// 父亲是 爷爷 的左孩子if (parent == Grandfather->_left) {Node* Uncle = Grandfather->_right;// 叔叔是 红色:三人变色,cur指爷if (Uncle && Uncle->_col == RED) {parent->_col = BLACK;Uncle->_col = BLACK;Grandfather->_col = RED;cur = Grandfather;parent = cur->_parent;}// 叔叔是 黑色:旋转后变色else if (Uncle == nullptr || Uncle->_col == BLACK) {// 看 cur 的位置:决定单旋 or 双旋if (cur == parent->_left) { /* 右单旋 + 变色gp uc*/rotateLL(Grandfather);// 爷变红,父变黑Grandfather->_col = RED;parent->_col = BLACK;}else if (cur == parent->_right) {/* 双旋(先左旋后右旋) + 变色gp uc*/rotateRR(parent); // p 先 左旋rotateLL(Grandfather); // g 再右旋// 爷变红,cur 变黑Grandfather->_col = RED;cur->_col = BLACK;}break;}}// 父亲是 爷爷 的右孩子else if (parent == Grandfather->_right) {Node* Uncle = Grandfather->_left;// 叔叔是 红色:三人变色,cur指爷if (Uncle && Uncle->_col == RED) {parent->_col = BLACK;Uncle->_col = BLACK;Grandfather->_col = RED;cur = Grandfather;parent = cur->_parent;}// 叔叔是 黑色:旋转后变色else if (Uncle == nullptr || Uncle->_col == BLACK) {// 看 cur 的位置:决定单旋 or 双旋if (cur == parent->_right) {/* 左单旋 + 变色gu pc*/rotateRR(Grandfather);// 爷变红,父变黑Grandfather->_col = RED;parent->_col = BLACK;}else if (cur == parent->_left) {/* 双旋(先右旋后左旋) + 变色gu pc*/rotateLL(parent); // p 先 右旋rotateRR(Grandfather); // g 再左旋// 爷变红,cur 变黑Grandfather->_col = RED;cur->_col = BLACK;}break;}}}// 修改一:根节点强制变色_root->_col = BLACK;return make_pair(iterator(newNode, _root), true);}// RR型:左单旋void rotateRR(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;// 1、subRL变成parent的右孩子parent->_right = subRL;// subRL 是有可能为 空的if (subRL) {subRL->_parent = parent;}// 2、parent变成subR的左孩子subR->_left = parent;parent->_parent = subR;// 3、subR变成当前子树的根// parentParent 是指 刚开始的 parent 的父亲:若 parent 是 _root 则 parentParent 为空,否则不为空,则该树就是子树if (parentParent) {if (parent == parentParent->_right)parentParent->_right = subR;else parentParent->_left = subR;subR->_parent = parentParent;}// 如果 parentParent == nullptr:说明 parent 是该树的 _root,_root 的 parent 是空else {_root = subR;subR->_parent = nullptr;}}// LL型:右单旋void rotateLL(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;// 1、subLR变成parent的左孩子parent->_left = subLR;// subRL 是有可能为 空的if (subLR) {subLR->_parent = parent;}// 2、parent变成subL的右孩子subL->_right = parent;parent->_parent = subL;// 3、subL 变成当前子树的根// parentParent 是指 刚开始的 parent 的父亲:若 parent 是 _root 则 parentParent 为空,否则不为空,则该树就是子树if (parentParent) {if (parent == parentParent->_right)parentParent->_right = subL;else parentParent->_left = subL;subL->_parent = parentParent;}// 如果 parentParent == nullptr:说明 parent 是该树的 _root,_root 的 parent 是空else {_root = subL;subL->_parent = nullptr;}}// LR 型:subL 先 左旋, parent 右旋void rotateLR(Node* parent) {rotateRR(parent->_left);rotateLL(parent);}// RL 型:subR 先 右旋, parent 左旋void rotateRL(Node* parent) {rotateLL(parent->_right);rotateRR(parent);}// 中序遍历void InOrder() {_InOrder(_root);cout << '\n';}// 获取根节点Node* GetRoot() {return _root;}// 获取该树的高度int Height() {return _Height(_root);}// 获取节点个数int Size() {return _Size(_root);}// 判断是否是 红黑树bool IsValidRBTree() {if (_root == nullptr) return false;else if (_root && _root->_col == RED) return false;// 遍历一条路,记录一条路上一共固定有多少个黑色节点int cnt = 0;Node* cur = _root;while (cur) {if (cur->_col == BLACK) cnt++;cur = cur->_left;}return _IsValidRBTree(_root, 0, cnt);}private:// 判断是否是 红黑树bool _IsValidRBTree(Node* pRoot, size_t k, const size_t blackCount){// 1、看根节点是否是 黑的// 2、看每条路径的 黑色节点数量是否相同// 3、检查是否有连续的红节点:遇到一个红节点就判断其父亲是否是 红的//走到null之后,判断 k 和 blackCount 是否相等:即一条路径上的 黑色节点数量是否为固定值if (pRoot == nullptr){if (k != blackCount){cout << "违反性质四:每条路径中黑色节点的个数必须相同" << endl;return false;}return true;}// 统计黑色节点的个数if (pRoot->_col == BLACK)k++;// 检测当前节点与其双亲是否都为红色Node* pParent = pRoot->_parent;if (pParent && pParent->_col == RED && pRoot->_col == RED){cout << "违反性质三:没有连在一起的红色节点" << endl;return false;}return _IsValidRBTree(pRoot->_left, k, blackCount) && _IsValidRBTree(pRoot->_right, k, blackCount);}int _Size(Node* pRoot) {if (pRoot == nullptr) return 0;//if (pRoot->_left == nullptr && pRoot->_right == nullptr) return 1;return 1 + _Size(pRoot->_left) + _Size(pRoot->_right);}int _Height(Node* pRoot) {if (pRoot == nullptr)return 0;return 1 + max(_Height(pRoot->_left), _Height(pRoot->_right));}// 销毁一棵树:后序遍历void destory(Node* root) {if (root == nullptr) {return;}destory(root->_left);destory(root->_right);delete root;}// 拷贝一棵树Node* CopyTree(const Node* root) {if (root == nullptr) {return nullptr;}Node* newRoot = new Node(root->_kv);newRoot->_left = CopyTree(root->_left);newRoot->_right = CopyTree(root->_right);return newRoot;}void _InOrder(const Node* root) {if (root == nullptr) {return;}_InOrder(root->_left);cout << (root->_kv).first << " : " << (root->_kv).second << '\n';_InOrder(root->_right);}Node* _root = nullptr;
};6. ⭐封装 set 完整代码
红黑树的代码 前面已经实现,在 set 中直接调用一个红黑树即可(记得在 set.h 要放入 红黑树的头文件 )
template<class K>
class set
{struct set_KeyOfT {const K& operator()(const K& key) {return key;}};
public:typedef typename RBTree<K, const K, set_KeyOfT>::iterator iterator;typedef typename RBTree<K, const K, set_KeyOfT>::const_iterator const_iterator;// 直接调用红黑树的 插入函数pair<iterator, bool> insert(const K& key) {return _tree.insert(key);}// 迭代器:都是直接调用底层红黑树的 函数iterator begin() {return _tree.begin();}iterator end() {return _tree.end();}const_iterator begin() const {return _tree.begin();}const_iterator end() const {return _tree.end();}iterator find(const K& key) {return _tree.find(key);}private:RBTree<K, const K, set_KeyOfT> _tree;
};7. ⭐封装 map 完整代码
红黑树的代码 前面已经实现,在 map 中直接调用一个红黑树即可(记得在 map .h 要放入 红黑树的头文件 )
template<class K, class V>
class map
{struct map_KeyOfT {const K& operator()(const pair<K, V>& kv) {return kv.first;}};
public:typedef typename RBTree<K, pair<const K, V>, map_KeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, map_KeyOfT>::const_iterator const_iterator;pair<iterator, bool> insert(const pair<K, V>& kv) {return _tree.insert(kv);}// 迭代器iterator begin() {return _tree.begin();}iterator end() {return _tree.end();}const_iterator begin() const {return _tree.begin();}const_iterator end() const {return _tree.end();}iterator find(const K& key) {return _tree.find(key);}V& operator[](const K& key) {pair<iterator, bool> pr = insert(make_pair(key, V()));return pr.first->second;}private:RBTree<K, pair<const K, V>, map_KeyOfT> _tree;
};
相关文章:

【C++ 第十五章】map 和 set 的封装(封装红黑树)
1. map 和 set 的介绍 ⭐map 与 set 分别是STL中的两种序列式容器; 它们是一种树形数据结构的容器,且其的底层构造为一棵红黑树; 而在上一篇文章中提到,其实红黑树本身就是一棵二叉搜索树,是基于二叉搜索树的性质对其增加了平衡的属性来提高其综合性能 ⭐当然也…...

LIN通讯
目录 1 PLinApi.h 2 TLINFrameEntry 结构体 3 自定义函数getTLINFrameEntry 4 TLINScheduleSlot 结构体 5 自定义函数 getTLINScheduleSlot 6 自定义LIN_SetScheduleInit函数 7 自定义 LIN_StartSchedule 8 发送函数 9 线程接收函数 1 PLinApi.h 这是官方头文件 ///…...
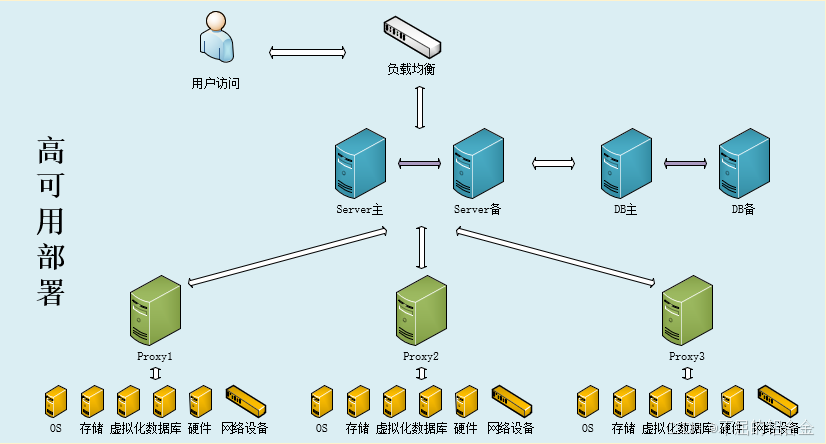
zabbix常见架构及组件
Zabbix作为一个开源的、功能全面的监控解决方案,广泛应用于各类组织中,以实现对网络、服务器、云服务及应用程序性能的全方位监控。部署架构灵活性高,可支持从小型单一服务器环境到大型分布式系统的多种场景。基本架构通常包括监控端…...
plsql表格怎么显示中文 plsql如何导入表格数据
在Oracle数据库开发中,PL/SQL Developer是一款广泛使用的集成开发环境(IDE),它提供了丰富的功能来帮助开发人员高效地进行数据库开发和管理。在使用PL/SQL Developer时,许多用户会遇到表格显示中文的问题,以…...

chromedriver下载地址大全(包括124.*后)以及替换exe后仍显示版本不匹配的问题
Chrome for Testing availability CNPM Binaries Mirror 若已经更新了系统环境变量里的chromdriver路径下的exe,仍显示版本不匹配: 则在cmd界面输入 chromedriver 会跳出version verison与刚刚下载好的exe不匹配,则再输入: w…...

拦截器实现 Mybatis Plus 打印含参数的 SQL 语句
1.实现拦截器 package com.sample.common.interceptor;import com.baomidou.mybatisplus.extension.plugins.inner.InnerInterceptor; import lombok.extern.slf4j.Slf4j; import org.apache.ibatis.executor.Executor; import org.apache.ibatis.mapping.BoundSql; import or…...

Oracle Subprogram即Oracle子程序
Oracle Subprogram,即Oracle子程序,是Oracle数据库中存储的过程(Procedures)和函数(Functions)的统称。这些子程序是存储在数据库中的PL/SQL代码块,用于执行特定的任务或操作。下面详细介绍Orac…...

自然语言处理实战项目30-基于RoBERTa模型的高精度的评论文本分类实战,详细代码复现可直接运行
大家好,我是微学AI,今天给大家介绍一下自然语言处理实战项目30-基于RoBERTa模型的高精度的评论文本分类实战,详细代码复现可直接运行。RoBERTa模型是由 Facebook AI Research 和 FAIR 的研究人员提出的一种改进版的 BERT 模型。RoBERTa 通过采用更大的训练数据集、动态掩码机…...
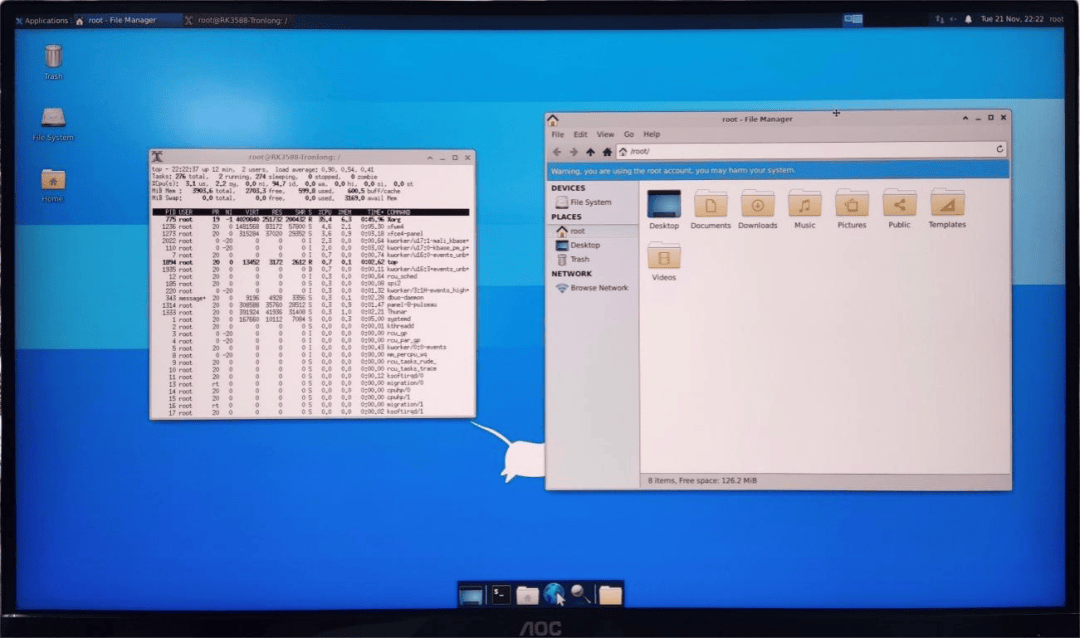
RK3588J正式发布Ubuntu桌面系统,丝滑又便捷!
本文主要介绍瑞芯微RK3588J的Ubuntu系统桌面演示,开发环境如下: U-Boot:U-Boot-2017.09 Kernel:Linux-5.10.160 Ubuntu:Ubuntu20.04.6 LinuxSDK: rk3588-linux5.10-sdk-[版本号] (基于rk3…...
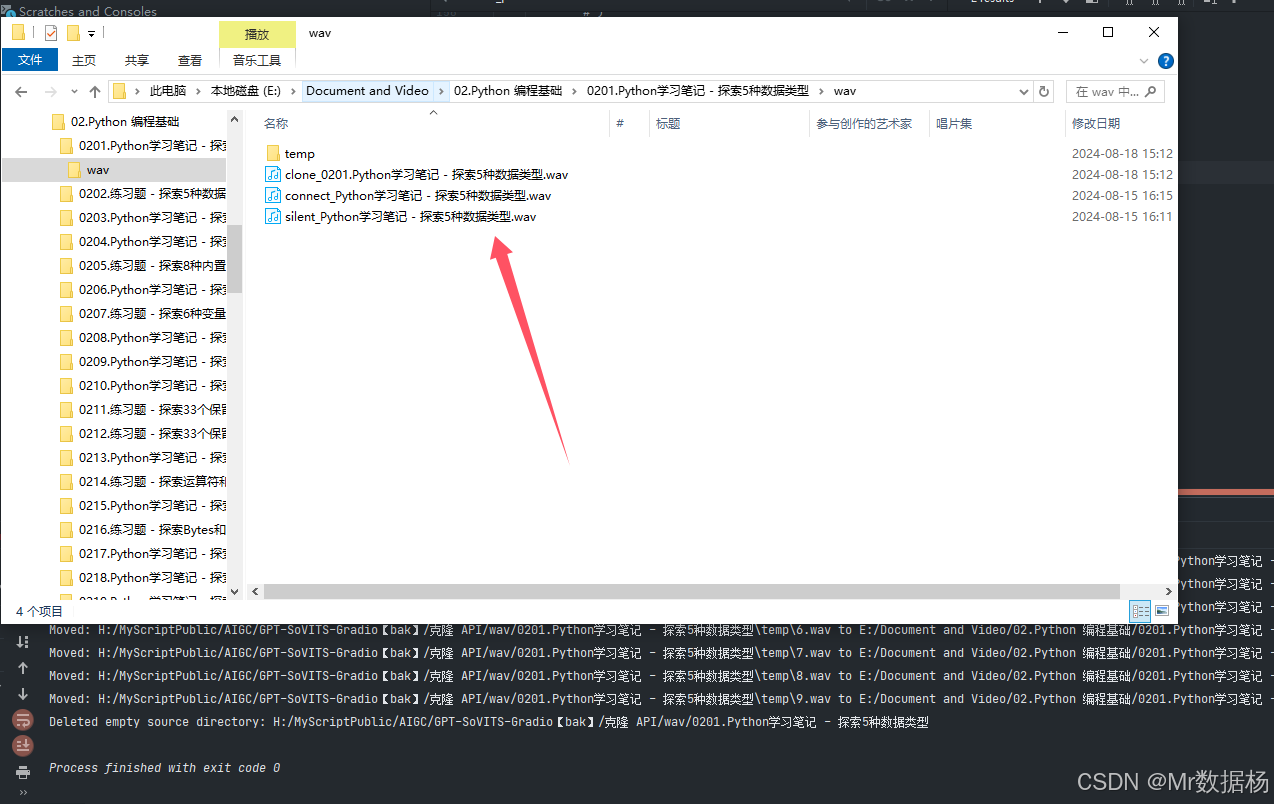
基于GPT-SoVITS的API实现批量克隆声音
目标是将每一段声音通过GPT-SoVITS的API的API进行克隆,因为拼在一起的整个片段处理会造成内存或者缓存溢出。 将目录下的音频文件生成到指定目录下,然后再进行拼接。 通过AI工具箱生成的数据文件是这样的结构,temp目录下是没个片段生成的部分,connect_是正常拼接的音频文件…...
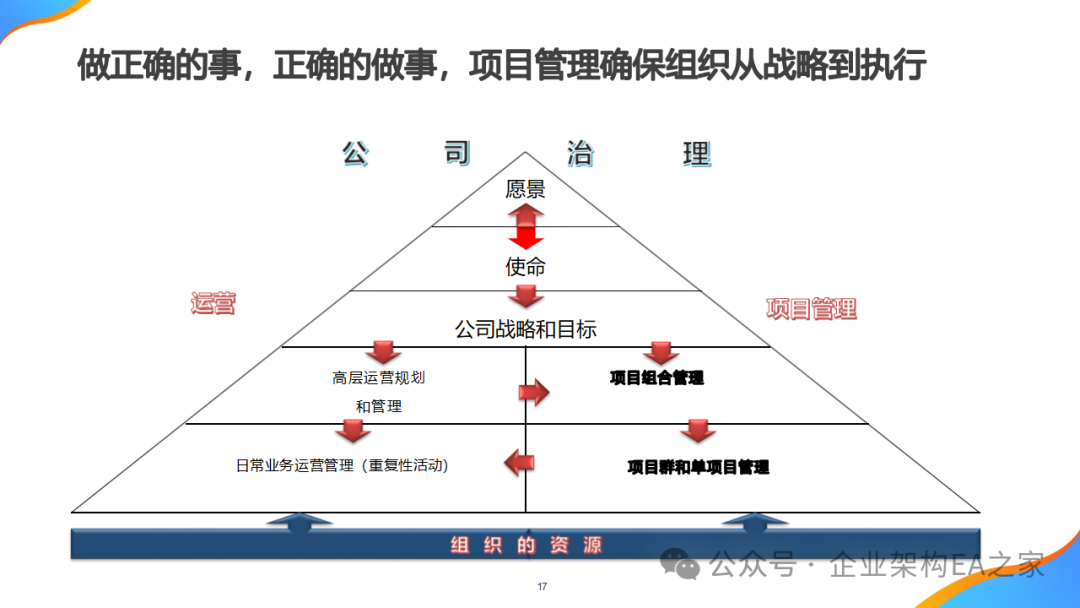
详解华为项目管理,附华为高级项目管理内训材料
(一)华为在项目管理中通过有效的沟通、灵活的组织结构、坚持不懈的努力、细致的管理和科学的考核体系,实现了持续的创新和发展。通过引进先进的管理模式,强调以客户需求为导向,华为不仅优化了技术管理和项目研发流程&a…...
脚本)
Perl(Practical Extraction and Reporting Language)脚本
Perl(Practical Extraction and Reporting Language)是一种非常灵活的脚本语言,主要用于文本处理、系统管理以及快速原型开发等领域。Perl 脚本可以用来执行一系列任务,包括文件操作、网络通信、数据处理等。 下面是一些关于编写…...

单例模式详细
文章目录 单例模式介绍八种方式1、饿汉式(静态常量)2、饿汉式(静态代码块)3、懒汉式(线程不安全)4、懒汉式(线程安全,同步方法)5、懒汉式(线程不安全…...
Unity3D 自定义窗口
Unity3D 自定义窗口的实现。 自定义窗口 Unity3D 可以通过编写代码,扩展编辑器的菜单栏和窗口。 简单的功能可以直接一个菜单按钮实现,复杂的功能就需要绘制一个窗口展示更多的信息。 编辑器扩展的脚本,需要放在 Editor 文件夹中。 菜单栏…...
dubbo:dubbo整合nacos实现服务注册中心、配置中心(二)
文章目录 0. 引言1. nacos简介及安装2. 注册中心实现3. 配置中心实现4. 源码5. 总结 0. 引言 之前我们讲解的是dubbozookeeper体系来实现微服务框架,但相对zookeeper很多企业在使用nacos, 并且nacos和dubbo都是阿里出品,所以具备一些天生的契合性&#…...

个人博客指路
Pudding 个人博客 比较懒,直接 github page 了,没国内代理加速。 欢迎大佬们,踩一踩 没做留言,觉得很鸡肋。有问题可以在本文底下评论、或者直接邮件...
【STM32 HAL】多串口printf重定向
【STM32 HAL】多串口printf重定向 前言单串口printf重定向原理实现CubeMX配置Keil5配置 多串口printf重定向 前言 在近期项目中,作者需要 STM32 同时向上位机和手机发送数据,传统的 printf 重定向只能输出到一个串口。本文介绍如何实现 printf 同时输出…...

帆软报表,达梦数据库驱动上传失败
1、按照正常操作新建数据库连接,上传准备好的达梦驱动时,提示如图一需要修改SystemConfig.driverUpload为true才可以。 2、FineDB存储了数据决策系统中除平台属性配置以外的所有信息。详情请参见: FineDB 数据库简介。 3、因此管理员可通过…...

CSS选择器的优先级是如何确定的?有哪些方法可以提高选择器的效率?
CSS选择器的优先级是如何确定的? CSS选择器的优先级决定了当多个选择器同时应用于一个元素时,哪个选择器将最终生效。CSS选择器的优先级由多个因素决定,主要包括以下几个方面: 特殊性(Specificity) 特殊性…...
)
【MySQL】基础入门(第二篇)
1.MySQL基本数据类型 数值类型 MySQL 支持所有标准 SQL 数值数据类型。 这些类型包括严格数值数据类型(INTEGER、SMALLINT、DECIMAL 和 NUMERIC),以及近似数值数据类型(FLOAT、REAL 和 DOUBLE PRECISION)。 关键字INT是INTEGER的同义词,关键字DEC是D…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
