建筑物规则化(实现) --- 特征边分组、重构、直角化
规则化建筑物
一、摘 要
建筑物多边形在地图综合中的两类处理模型:化简与直角化。
建筑物矢量数据来源广泛,在数据获取过程中,受GPS精确度、遥感影像分辨率或人为因素的影响,数据往往存在不同程度的误差。其中,图像分割、深度学习等技术提取的建筑物多边形边界由任意折线构成,直角特征弱,点数冗余,无法实现地理信息的规范化表达。本文讨论此类轮廓模糊建筑物的化简问题。
1.1 ArcGIS 规则化建筑物覆盖区 (3D Analyst)
通过消除几何中不需要出现的伪影来对建筑物覆盖区面的形状进行规范化。

1.2 supermap 建筑物规则化
通过提取建筑物的关键点及建筑物主方向,对建筑物覆盖区面的轮廓线进行规则化,用于消除建筑物范围几何中不规整的边界及细节。

1.3 学术学报 轮廓规则化
(1)基于特征边重构的建筑物化简方法;
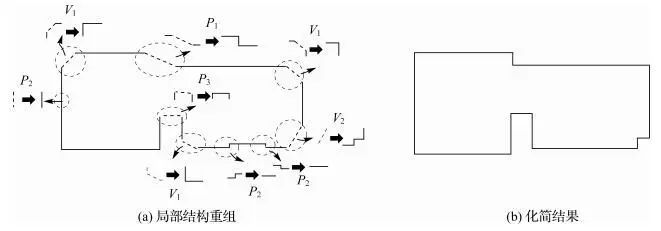
(2)基于最小二乘的建筑物多边形的化简与直角化。
建筑物的规则化处理,主要包括三个步骤:将特征边分组、重构,实现建筑物的有效化简,最后对化简后的多边形进行直角化处理。
二、特征边分组
对待化简(规则化处理)的多边形,按某种规则,对多边形节点进行分组,通过分组节点获取特征边分组。
2.1 基于面主方向的特征边分组
定义建筑物多边形中若干能控制多边形整体轮廓的边为特征边。以各边与主方向的夹角作为约束对建筑物轮廓进行了详细的划分。
01 主方向
统计加权方法计算主方向考虑多边形每条边的方向和长度,避免了长边误差的干扰,其描述如下:
①测试0°至90°之间相差固定步长(步长取决于所需的结果精度,如1°)的一系列候选方向。
②对于每个候选方向,计算各边贡献值,候选方向的权重是每条边贡献值的总和。
如下图,OA为候选方向,角度偏差系数为α。将多边形每条边平移,使其以点O为起点,若该边或其垂边在OB、OC范围内,则参与贡献值计算。多边形某边平移后为OD,由于在OB、OC范围外,贡献值为0;OE在范围内,长度为li,与OA夹角为β,则OE对候选方向OA的贡献值Li为:
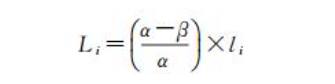
统计加权法示意图如下:
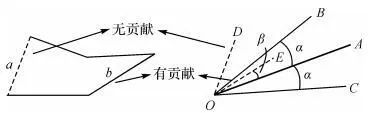
02 特征边分组
设定边长系数l1、l2(l1>l2),特征边必须满足以下条件之一:
①边长大于l1;
②与主方向垂直或平行,且边长大于l2;
③存在与其垂直的邻边,且边长大于l2。保留多边形中的较长边有利于保持轮廓准确性,较长边的重构通常导致多边形变化过大,因此设置边长系数l1将此类边分类为特征边。通常l1为平均边长,l2用来约束化简程度。
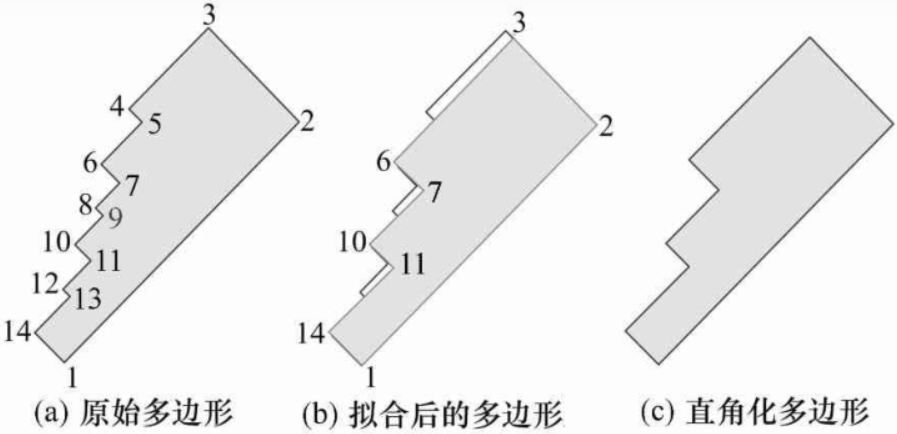
建筑物多边形中一条或连续几条非特征边为待化简弧段。以下图为例,特征边分组的过程如下:
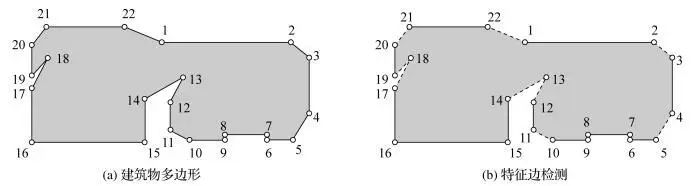
(1) 遍历建筑物多边形点集合,判断相邻两点间线段与主方向的空间关系并计算两点间距,若该线段不是特征边,记录首点点号,得到非特征边点集合S1{2, 4, 6, 8, 10, 12, 13, 17, 18, 20, 22}。
(2) 根据集合S1计算待化简弧段的点集合,得到集合S2{[2, 3], [4, 5], [6, 7], [8, 9], [10, 11], [12, 13, 14], [17, 18, 19], [20, 21], [22, 1]}。
(3) 待化简弧段两侧特征边的组合集S3为{[1, 2;3, 4], [3, 4;5, 6], [5, 6;7, 8], [7, 8;9, 10], [9, 10;11, 12], [11, 12;14, 15], [16, 17;19, 20], [19, 20;21, 22], [21, 22;1, 2]}。
2.2 基于距离阈值和直角约束的特征点分组
建筑物多边形主要是由相互垂直的弧段构成,一般可分解成多个大小不一的矩形。
对其化简的目的是在保持多边形整体轮廓一致的前提下,删除若干个小的凸起矩形,补平若干个凹陷矩形。
在多边形的点集中,总存在若干能控制多边形整体轮廓的点,这些点相对其它点而言,化简后位移距离较小,本文称这些点为建筑物多边形的特征点。
对常规的地图,可根据比例尺计算出最小可视距离,但在多尺度地图综合中最小可视的实地距离不仅与目标比例尺有关,而且与源地图的比例尺有关。这里按“自然规律”的综合法则来计算。
01 最小可视距离阈值的计算
F= St*D[ 1 - Ss/ St ] ,
式中:
F为目标比例尺下图上最小可视距离对应的实地距离;
St为目标比例尺分母;
D为最小可视的距离,取值为0.3~0. 6 mm;
Ss为源数据比例尺分母.
在源比例尺为1 :2 000、目标比例尺为1∶1万,取最小可视距离D=0. 4 mm ,计算得F=3. 2m。
02 特征点分组
建筑物分组的具体步骤:
(1)将多边形的坐标点按逆时针方向排序;N为多变形点的总数。设置4个变量A、B、E、F表示当前要判断边的点号,其中A、B用于顺时针方向搜索,E、F用于反时针方向搜索。设置变量s表示第1组的起点。
(2)找到最长的一条边,该边两个端点的序号为n, n+1 ,初始化一个整数链表LIST,将n, n+ 1插入该链表。令A= E= n,B = F= n+1;
(3)沿A向顺时针方向搜索两个点,其点号:A=(A - 2)%N,B = (B - 2)% N ;
(4)在LIST对应的点构成的弧段中,存在若干与A - B平行(包括近似)的弧段,计算AB到这些弧段的最大距离d ;以及A→B到n →n+1的夹角a;
(5)如果d >F或者d <F且a >0°,表示已找到第1组的起点,则令S = (A +2)%N,继续搜索F的下两点,其点号E= (E+ 2) % N,F= (F+ 2) % N,到步骤6;否则在LIST首位置加入B、A,继续向上搜索,回到步骤3;
(6)如果F=S,则分组完毕,结束探测。否则,与步骤3一样,计算EF到与之平行的弧段的最大距离d以及E→F到n →n+1的夹角α;
(7)如果d >F或者d <F且a >0°,则该组搜索完毕,开始探测下一组,重新初始化一个新链表LIST,向前进方向搜索新组。如果不满足上述条件,则将E、F加入到LIST,令 E=(E+2)% N,F=(F+2)% N,回到步骤5。
对建筑物多边形的点进行分组,如下图所示:
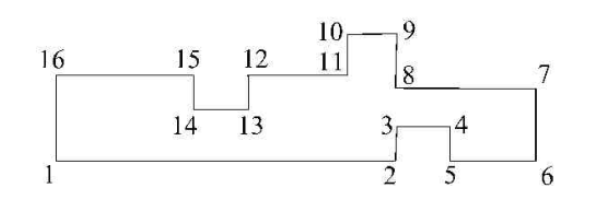
多边形的点分成了4个组:( 1、2、3 、4 、5 、6), (6、7),(7 、8、 9、 10、11、 12、13 、14、15、16) , (16、1 ) 。
三、特征边重组原则
基于特征边组合的判别和重组来化简建筑物多边形,基本目标是实现建筑物多边形与影像建筑物边界最大程度的套合,并尽可能保持面积和形态特征。因此,结构重组时按照以下原则:
原则1:用边长系数l2和局部区域面积l3(l3=l22)约束化简程度。
原则2:结构重组是一个循环的过程,每处理完一个局部结构,更新多边形,再次进行特征边分组、重构,直到特征边组合集为空集。
原则3:对于凹凸结构不进行夸大处理,若满足删除(填充)条件,删除(填充)后循环过程将再次判别并处理此弧段。
四、结构重组
对分组后的每组特征边,都需要提取一条线段来代替这一组折线边集合,可以采取特征点拟合直线、或凸多边形最窄宽度提取中心线等实现。将分组提取替代线按一定的规则,进行连接处理,便可实现结构的重组。
由于特征边与主方向的关系多为平行或垂直,待化简弧段两侧特征边的空间关系组合可抽象为3种,分别为平行结构、垂直结构和其他结构。
判断邻近替代线的空间关系,以夹角、位置作为选择化简规则的条件,通过局部结构重组实现化简。化简示意图如下:
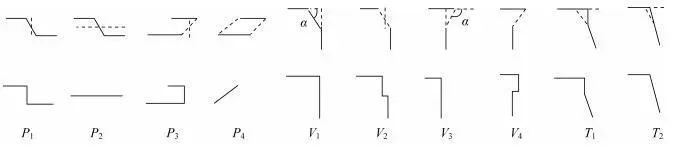
4.1 平行结构
P1、P2、P3、P4为平行结构,待化简弧段两侧特征边平行。
(1)若两边间距大于l2,过待化简弧段中点向两侧作垂线,如P1、P3。
(2)否则,判断两边夹角,若夹角为0°,采用最小二乘法将该结构(包括待化简弧段)的点拟合成直线替代该结构,如P2(理论上不存在);
(3)若夹角为180°,该结构面积小于l3,连接端点,删除凸起(填充凹陷)的部位,如P4,若该结构面积大于l3,按P3处理。
4.2 垂直结构
V1、V2、V3、V4为垂直结构,待化简弧段两侧特征边垂直。
(1)V1、V3结构中,α小于90°,计算两边交点,若该点与邻近两点组成区域面积小于l3,则添加交点,如V1;
(2)否则, 取虚线中点,向两侧作垂线,如V2。若α大于90°,如V3、V4,若两边交点与邻近两点组成的区域面积小于l3,添加交点,删除右侧区域,如V3,否则,取虚线中点,如V4。
4.3 其他结构
T1、T2为其他结构,两特征边既不垂直也不平行。计算斜边一点到另一边的距离,若距离大于l2,添加垂线与另一边的交点,如T1,否则直接添加交点,如T2。
五、直角化规则
若建筑物目标中两相邻边满足规则化空间关系,判断两边与主方向的关系,以主方向为基准进行直角化处理。直角化规则如下:
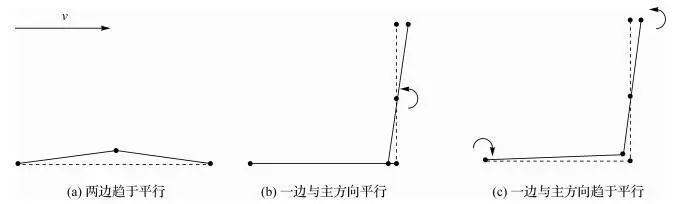
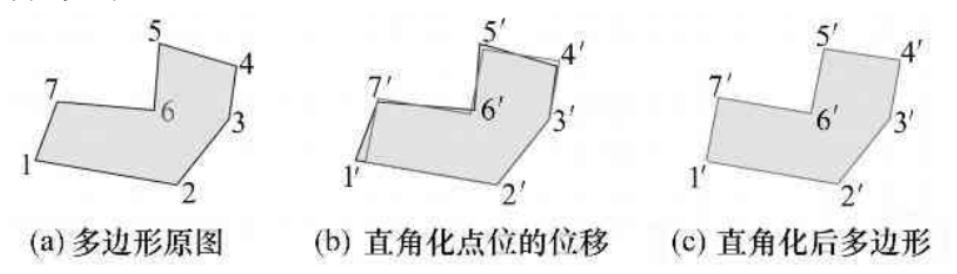
(1) 若两边共线或趋于平行,则移除中间点,如图 (a)所示。
(2) 若两边趋于垂直,其中一边与主方向平行或垂直,将另一边绕其中点旋转至二者垂直,如图 (b)所示。
(3) 若两边趋于垂直,其中一边与主方向趋于平行或趋于垂直,将其绕端点旋转至主方向或主方向的垂直方向,另一边绕中点旋转至二者垂直,顶点移至二者交点,如图 (c)所示。
(4) 若两边趋于垂直,且两边均不与主方向接近平行或垂直,将较短边绕中点旋转至二者垂直。
六、建筑物规则化(实现) --- 特征边分组、重构、直角化
ME & OTHERS
虚心学习、借鉴、优化
在虚心学习了大家的成果后,畅想着“建筑物规则化”在制图和数据规则化上有很好的应用需求,规则化后的建筑物轮廓,在使用“建筑物2.5D效果”工具时,不但因为节点的减少提高工具分析性能,还因为直角化让建筑物更加规范、立体。
最重要的是,基于特征分组和规则化允许偏移距离的融合,让我豁然开朗,不仅可以用来处理具有正交特性的建筑物,还可以拓展用于简化非正交的,曲线特征的图形。如通过影像实例分割得到的水系、道路等数据。
具体算法和实现在后续的文章中讲解。本文给出实现的过程视频。
本文基于下图,演示特征边分组、重构和直角化的实现过程。
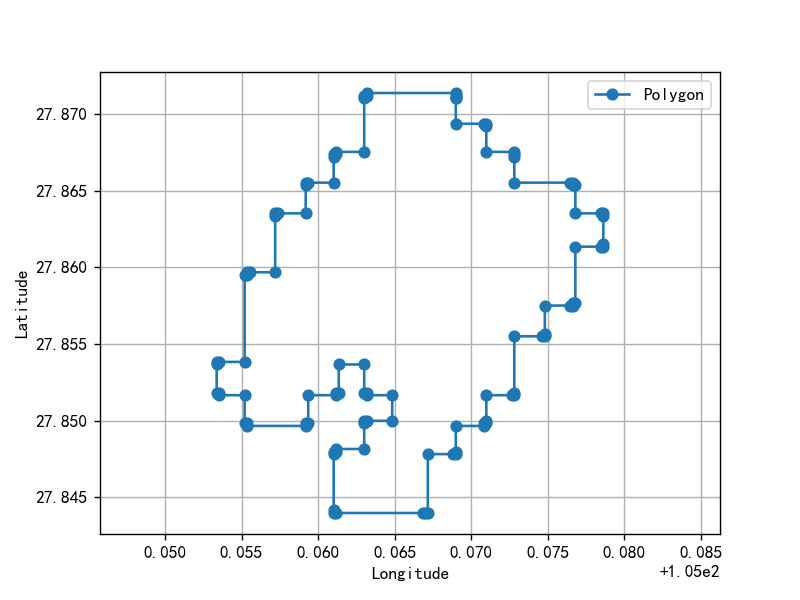
6.1 基于偏移距离的特征边分组
假设我们有一支很粗的笔,沿着多边形边界绘制,当前画笔定能掩盖需要被简化的短边、不规则折线。
当绘制建筑物轮廓时,应确保绘制线段保持直线连接。绘制曲线段时,确保曲线的平滑过渡。
6.2 特征分组重构
特征边重构,由于考虑的是“笔画”遮盖的效果,故提取笔画的中心线作为重构线结果,比使用“基于最小二乘平差模型的线性拟合”更加符合小编的算法设计。
因此,可将重构算法转为凸多边形最小宽度算法+凸多边形在指定方向上的中心线提取。
凸多边形的宽度定义为平行切线间的最小距离,可使用“旋转卡壳”算法实现。
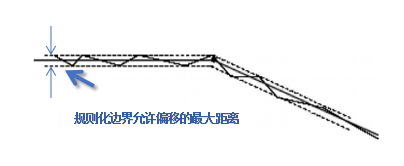
凸多边形在垂直于最小宽度方向上的中心线提取,可使用分组起始点和结束点在方向单位向量上的投影点获取。
分组特征边计算重构线算法示意如下图:
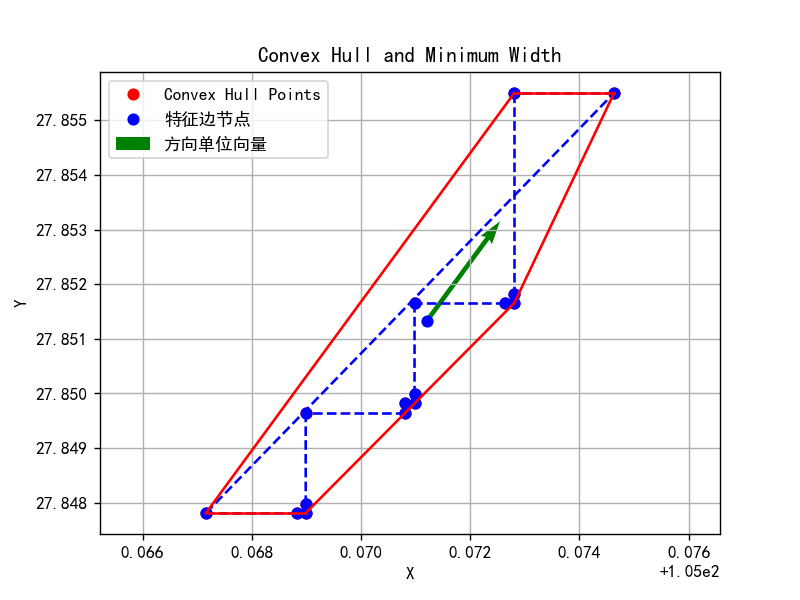
重构线结果示意如下图:
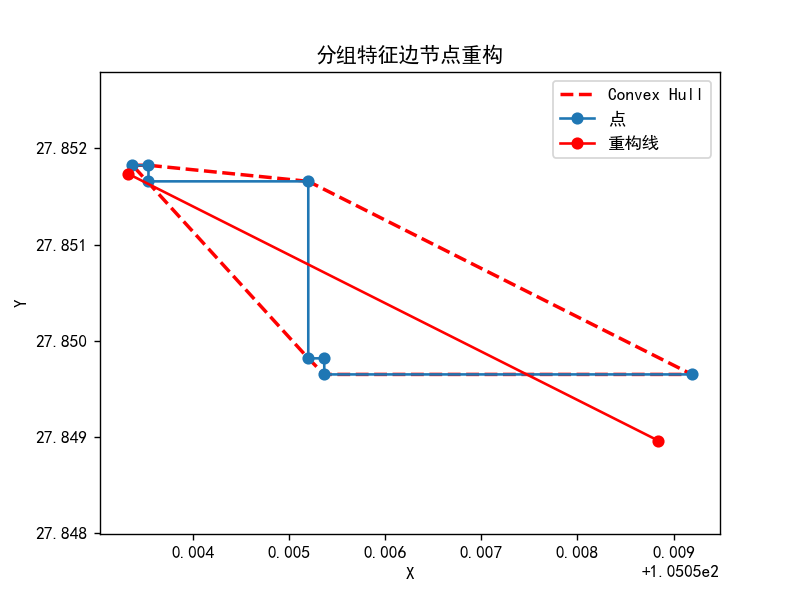
特征边分组、重构过程(迭代)演示如下
6.3 多边形直角化
由于并非所有建筑物的内角均应为直角,且其长边与短边在直角化处理中影响力(权)不同,因此,可使用带限制条件的建筑物多边形不等权的局部直角化的最小二乘算法实现建筑物的直角化。
建筑物多边形直角化过程示意如下图:
直角化过程(迭代)演示如下:

相关文章:

建筑物规则化(实现) --- 特征边分组、重构、直角化
规则化建筑物 一、摘 要 建筑物多边形在地图综合中的两类处理模型:化简与直角化。 建筑物矢量数据来源广泛,在数据获取过程中,受GPS精确度、遥感影像分辨率或人为因素的影响,数据往往存在不同程度的误差。其中,图像分割、深度学习…...

pytorch的优化
在pytorch中,tensor是基于numpy与array的。内存共享。 在pythorch中,自定义层是继承nn.Module。将层与模型看成是模块,层与模型堪称模块,两者之间没有明确界限,定义方式与定义模型一样_init_与forward。 1、先定义全…...

React 入门第一天:从Vue到React的初体验
作为一名合格的前端工程师,怎么能只会Vue呢?学习React不仅是一场新技术的探索,更是对前端开发思维的一次重新审视。在这里,我将分享学习React的心得,希望能帮助那些和我一样从Vue转向React的开发者。 1. 为什么选择Re…...

Golang | Leetcode Golang题解之第357题统计各位数字都不同的数字个数
题目: 题解: func countNumbersWithUniqueDigits(n int) int {if n 0 {return 1}if n 1 {return 10}ans, cur : 10, 9for i : 0; i < n-1; i {cur * 9 - ians cur}return ans }...
【Linux】 gdb-调试器初入门(简单版使用)
🔥系列文章:《Linux入门》 目录 一、背景 二、什么是GDB 🌷定义 🌷GDB调试工具---提供的帮助 三、GDB的安装教程-Ubuntu 🌷gdb的安装 四、哪类程序可被调试 🌷程序的发布方式 🌷Debug版…...

Spring 的事务支持
文章目录 1、Spring如何管理事务2、编程式事务1_基本用法2_创建TransactionTemplate实例3_TransactionTemplate的内部结构4_总结 3、声明式事务1_使用Transactional注解2_事务的传播行为3_配置4_总结 1、Spring如何管理事务 Spring为事务管理提供了一致的编程模板,…...
基于STM32开发的智能家居照明控制系统
目录 引言环境准备工作 硬件准备软件安装与配置系统设计 系统架构硬件连接代码实现 系统初始化传感器数据采集显示与控制逻辑Wi-Fi通信应用场景 家庭智能照明办公室节能照明控制常见问题及解决方案 常见问题解决方案结论 1. 引言 智能家居照明控制系统通过集成光照传感器、继…...

程序员的底层思维~张建飞
前言 ◆ 成人学习的目的不是获取更多的信息量,而是学习更好的思维模型。 ◆ 好的思维能力是可以被复制和迁移的,它应该是普适的,而不应该有行业的界限。 第一部分 基础思维能力 ◆ 因为语言的抽象性,我在团队中会要求大家使用通用…...

美股收涨,半导体板块领涨;苹果iPhone出货预测上调
市场概况 在昨夜的交易中,美股三大股指全线收涨。道琼斯工业平均指数上涨1.39%,纳斯达克综合指数上涨2.34%,标准普尔500指数上涨1.61%。值得注意的是,英伟达股票涨幅近4%,推动了科技股的整体表现。美国十年期国债收益…...

[学习笔记]在不同项目中切换Node.js版本
文章目录 使用 Node Version Manager (NVM)安装 NVM使用 NVM 安装和切换 Node.js 版本为项目指定 Node.js 版本 使用环境变量指定 Node.js安装多个版本的 Node.js设置环境变量验证配置使用 npm 脚本切换 在开发中,可能会遇到不同的Vue项目需要不同的Node.js…...

SOL项目开发代币DApp的基本要求、模式创建与海外宣发策略
Solana(SOL)作为一个高性能区块链平台,以其快速的交易速度和低交易成本吸引了大量开发者和投资者。基于Solana开发的去中心化应用程序(DApp)和代币项目正逐步成为区块链领域的重要组成部分。要成功开发并推广一个SOL项…...
如何在 FastReport .NET 中构建和安装 Postgres 插件
FastReport .NET 是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案。 功能非常丰富,功能广泛。今天我们将介绍如何使用报表设计器的 FastReport 插件连接数据库。 FastReport .NET 是适用于.NET Core 3,ASP.NET,MVC和Windows窗体…...
JVM指令重排序
文章目录 什么是指令重排序编译器优化JIT 编译优化处理器优化重排序数据依赖性 硬件层的内存屏障指令重排的代码验证好处减少管道阻塞提高缓存利用率利用并行执行单元性能提升更好地利用硬件资源 问题内存可见性问题编程复杂性增加调试困难 解决方案:Java内存模型&a…...

改造字典关键字:
怎样把第一个关键字的值都 加到所有关键字上? {type: 7, typenum: , typemon: } 我们可以使用字典的keys()方法来获取所有的关键字,然后通过遍历字典的方式将第一个关键字的值添加到其他关键字的名称上。以下是一个示例代码: data {type: …...

Neo4j 图数据库入门
图形数据库存储节点和关系,而不是表或文档。数据的存储方式就像你在白板上勾画想法一样。您的数据存储不受预定义模型的限制,允许以非常灵活的方式考虑和使用它。 一、核心概念:属性图形模型 Neo4j使用属性图数据库模型。图数据结构由节点(离…...
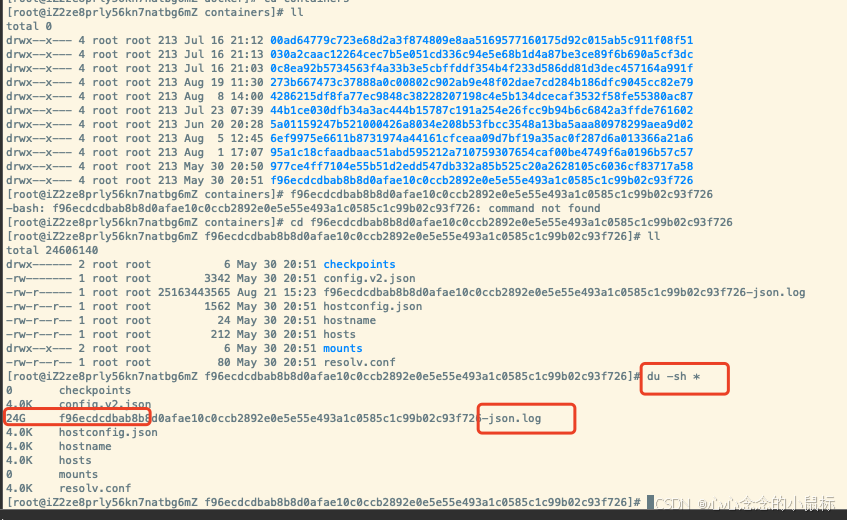
linux 磁盘满了,程序运行失败,如何处理?df -h
场景:紧急呼救,上传图片失败了。我一脸懵,服务器这是又咋地了,别邪乎姐姐,姐姐胆子小啊。 一、寻找问题原因 1、OSS出问题了? 然后我尝试了 IOS 的APP是没问题的,Android提示上传失败…...

Python编码系列—前端后浪:Python前后端分离开发实战指南
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...

Docker学习之路【五】了解数据卷
定义与特性 Docker数据卷是一个特殊目录,,用于实现容器间数据的持久化和共享。数据卷存在于宿主机上,可以被一个或多个容器使用。它独立于容器的生命周期,意味着即使容器被删除,数据卷中的数据也会保留。数据卷的主要…...

matlab如何设置产生的随机数一致
在MATLAB中,确保产生的随机数序列一致,通常需要使用随机数生成器的种子(seed)。通过设置相同的种子值,可以确保在每次运行代码时,随机数生成器从相同的初始状态开始,从而生成相同的随机数序列。…...

ansible --------拓展
编辑 hosts 配置文件 [rootmo ~]# vim /etc/ansible/hosts # 创建目录 [rootmo ~]# mkdir /etc/ansible/playbook # 编辑配置文件 [rootmo ~]# vim /etc/ansible/playbook/nginx.yml # 执行测试 [rootmo ~]# ansible-playbook /etc/ansible/playbook/nginx.yml roles 修…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
