深入理解支持向量机:从基本原理到实际应用
第6章 支持向量机
在本章中,我们将深入探讨支持向量机(SVM)这一强大的分类算法。SVM在模式识别和机器学习领域广泛应用,尤其在处理高维数据时表现出色。我们将依次讨论间隔与支持向量、对偶问题、核函数、间隔与正则化、支持向量量回归和核方法。
6.1 间隔与支持向量
支持向量机的核心思想是找到一个最佳超平面,将不同类别的数据分开。这个超平面使得两类之间的间隔最大化。设有两类样本点,分别为 C 1 C_1 C1和 C 2 C_2 C2,最佳超平面可以表示为:
w ⋅ x + b = 0 w \cdot x + b = 0 w⋅x+b=0
其中, w w w是法向量, x x x是样本点, b b b是偏置。间隔定义为到超平面的最短距离,表示为:
margin = 2 ∣ ∣ w ∣ ∣ \text{margin} = \frac{2}{||w||} margin=∣∣w∣∣2
通过最大化间隔,我们希望找到最优的 w w w和 b b b,使得:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 \min_{w,b} \frac{1}{2}||w||^2 w,bmin21∣∣w∣∣2
同时满足约束条件:
y i ( w ⋅ x i + b ) ≥ 1 , ∀ i y_i(w \cdot x_i + b) \geq 1, \forall i yi(w⋅xi+b)≥1,∀i
样本点中位于间隔边界上的样本称为支持向量,它们在确定超平面位置时起着关键作用。
6.2 对偶问题
为了更好地求解SVM的优化问题,我们引入拉格朗日乘子法,将原问题转化为对偶问题。我们定义拉格朗日函数为:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 m α i [ y i ( w ⋅ x i + b ) − 1 ] L(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum_{i=1}^{m} \alpha_i [y_i(w \cdot x_i + b) - 1] L(w,b,α)=21∣∣w∣∣2−i=1∑mαi[yi(w⋅xi+b)−1]
通过对 w w w和 b b b求偏导数并令其为零,我们可以得到对应的对偶问题:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i ⋅ x j ) \max_{\alpha} \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyj(xi⋅xj)
在约束条件:
∑ i = 1 m α i y i = 0 , α i ≥ 0 \sum_{i=1}^{m} \alpha_i y_i = 0, \quad \alpha_i \geq 0 i=1∑mαiyi=0,αi≥0
对偶问题的求解可以更加高效,尤其在样本数量较大时。
6.3 核函数
SVM的一个重要扩展是使用核函数来处理非线性可分问题。核函数通过隐式映射将输入空间映射到更高维的特征空间,从而使得原本非线性可分的问题在新空间中变得线性可分。常见的核函数包括:
- 线性核: K ( x i , x j ) = x i ⋅ x j K(x_i,x_j)=x_i \cdot x_j K(xi,xj)=xi⋅xj
- 多项式核: K ( x i , x j ) = ( γ x i ⋅ x j + r ) d K(x_i,x_j)=(\gamma x_i \cdot x_j + r)^d K(xi,xj)=(γxi⋅xj+r)d
- 高斯核(RBF核): K ( x i , x j ) = exp ( − ∣ ∣ x i − x j ∣ ∣ 2 2 σ 2 ) K(x_i,x_j)=\exp\left(-\frac{||x_i-x_j||^2}{2\sigma^2}\right) K(xi,xj)=exp(−2σ2∣∣xi−xj∣∣2)
在使用核函数时,我们只需要在对偶问题中替换点积$ x_i \cdot x_j 为核函数 为核函数 为核函数 K(x_i,x_j) $,从而避免直接计算高维特征。
6.4 间隔与正则化
在实际应用中,为了提高模型的泛化能力,我们引入正则化技术以防止过拟合。支持向量机的正则化形式为:
min w , b 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ξ i \min_{w,b} \frac{1}{2}||w||^2 + C \sum_{i=1}^{m} \xi_i w,bmin21∣∣w∣∣2+Ci=1∑mξi
其中, C C C为正则化参数, ξ i \xi_i ξi为松弛变量,用于处理分类错误。约束条件变为:
y i ( w ⋅ x i + b ) ≥ 1 − ξ i , ξ i ≥ 0 y_i(w \cdot x_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0 yi(w⋅xi+b)≥1−ξi,ξi≥0
通过调整参数 C C C,可以控制模型的复杂性。
6.5 支持向量量回归
支持向量机不仅可以用于分类,也可以用于回归问题。支持向量回归(SVR)旨在找到一个最佳的超平面,使得大多数数据点在这个超平面附近。SVR的目标是最小化以下损失函数:
min w , b , ξ 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 n ( ξ i + ξ i ∗ ) \min_{w,b,\xi} \frac{1}{2}||w||^2 + C \sum_{i=1}^{n} (\xi_i + \xi_i^*) w,b,ξmin21∣∣w∣∣2+Ci=1∑n(ξi+ξi∗)
其中, ξ i \xi_i ξi和 ξ i ∗ \xi_i^* ξi∗分别表示预测值与真实值的偏差。约束条件为:
y i − ( w ⋅ x i + b ) ≤ ϵ + ξ i y_i - (w \cdot x_i + b) \leq \epsilon + \xi_i yi−(w⋅xi+b)≤ϵ+ξi
( w ⋅ x i + b ) − y i ≤ ϵ + ξ i ∗ (w \cdot x_i + b) - y_i \leq \epsilon + \xi_i^* (w⋅xi+b)−yi≤ϵ+ξi∗
通过这种方式,SVR能够在给定的 ϵ \epsilon ϵ容忍度内进行有效的回归分析。
6.6 核方法
核方法是支持向量机的另一个重要概念,通过使用核函数,我们可以在不显式计算特征的情况下,完成复杂的分类和回归任务。核方法的核心思想是,通过计算核函数而非直接特征,降低计算复杂度,提高模型的灵活性。
在实际应用中,我们可以使用各种核函数来处理不同类型的数据,调整模型的超参数,以达到最佳的分类或回归效果。
总结
本章详细介绍了支持向量机的基本原理和应用,包括间隔与支持向量、对偶问题、核函数、间隔与正则化、支持向量量回归和核方法。支持向量机凭借其强大的性能和灵活性,在许多实际场景中得到了广泛应用。希望本章的内容能够帮助你深入理解支持向量机的工作机制与应用潜力。
相关文章:

深入理解支持向量机:从基本原理到实际应用
第6章 支持向量机 在本章中,我们将深入探讨支持向量机(SVM)这一强大的分类算法。SVM在模式识别和机器学习领域广泛应用,尤其在处理高维数据时表现出色。我们将依次讨论间隔与支持向量、对偶问题、核函数、间隔与正则化、支持向量…...

每天一题:洛谷P2041分裂游戏
题目描述 有一个无限大的棋盘,棋盘左下角有一个大小为 n 的阶梯形区域,其中最左下角的那个格子里有一枚棋子。你每次可以把一枚棋子“分裂”成两枚棋子,分别放在原位置的上边一格和右边一格。(但如果目标位置已有棋子,…...

简单的 curl HTTP的POSTGET请求以及ip port连通性测试
简单的 curl HTTP的POST&GET请求以及ip port连通性测试 1. 需求 我们公司有一个演示项目,需要到客户那边进行项目部署,项目部署完成后我们需要进行项目后端接口的测试功能,但是由于客户那边么有条件安装类似于postman这种的测试工具&am…...

ubuntu下快捷键启动程序
背景:公司自开发的软件,经常需要启动,每次去找目录启动很麻烦,所以想快捷启动 方法1: 通过编辑.baserc启动 例如启动程序是toolA, 放在/home/user/software/目录下,那么在~/.baserc里面加入一行代码 al…...

Yii2 init 初始化脚本分析
脚本目的: init 脚本主要的作用是:从 environments 目录中复制配置文件,确保应用适配不同环境(例如开发、生产环境等)。 工作流程: 获取 $_SERVER 的 argv 参数 加载 environments/index.php 文件&#…...

深入理解gPTP时间同步过程
泛化精确时间协议(gPTP)是一个用于实现精确时间同步的协议,特别适用于分布式系统中需要高度协调的操作,比如汽车电子、工业自动化等。 gPTP通过同步主节点(Time Master)和从节点(Time Slave)的时钟,实现全局一致的时间参考。 以下是gPTP实现主从时间同步的详细过程:…...

基于阿里云服务的移动应用日志管理方案—日志的上传、下载、存档等
前言 如题,基于阿里云服务(ECS、OSS)实现 APP 的用户日志上传以及日志下载的功能,提高用户反馈问题到研发去分析、定位、解决问题的整个工作流的效率。 术语 ECS: 云服务器ECS(Elastic Compute Service)…...

Python浪漫之画星星
效果图(动态的哦!): 完整代码(上教程): import turtle import random import time # 导入time模块# 创建一个画布 screen turtle.Screen() screen.bgcolor("red")# 创建一个海龟&a…...
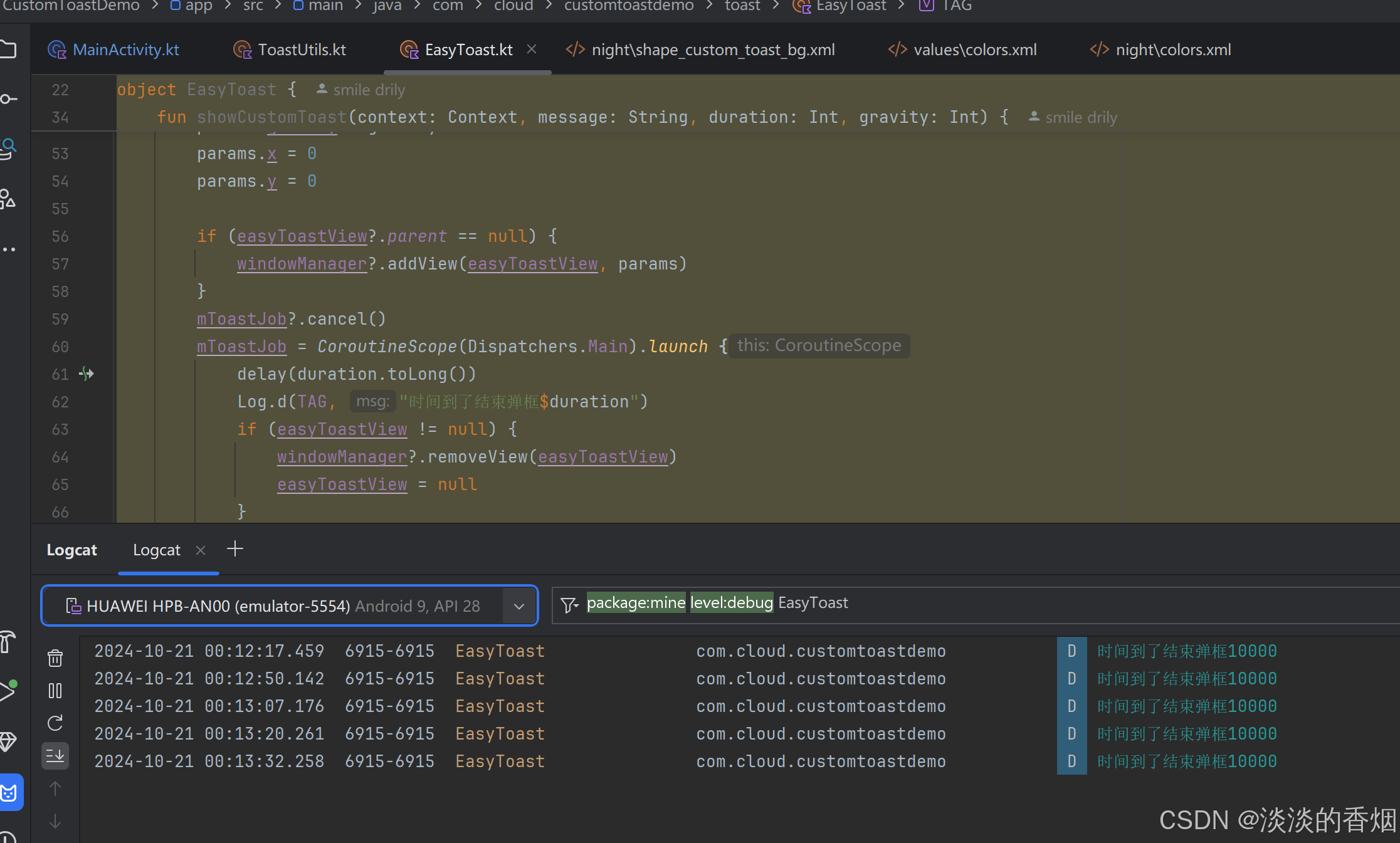
Android使用协程实现自定义Toast弹框
Android使用协程实现自定义Toast弹框 最近有个消息提示需要显示10s,刚开始使用协程写了一个shoowToast方法,传入消息内容、显示时间和toast显示类型即可,以为能满足需求,结果测试说只有5s,查看日志和源码发现Android系统中Toa…...

git diff命令详解
git diff 是 Git 中非常常用的命令,用于比较不同版本的文件改动。可以比较工作区、暂存区、或者提交之间的差异。下面是对 git diff 常用场景的详细解释: 1. git diff 当你执行 git diff 时,它会显示工作区与暂存区之间的差异,也…...

Vue 插槽:组件通信的“隐形通道”
在 Vue 中,插槽(slot)是实现组件内容分发的机制,允许我们将子组件的内容传递给父组件,从而提升组件的可复用性和灵活性。插槽的本质是通过将父组件内容传递到子组件指定的插槽位置,使得子组件在渲染时可以动…...

react1816中的setState同步还是异步的深层分析
setState 是 react 中更新 UI 的唯一方法,其内部实现原理如下: 调用 setState 函数时,React 将传入的参数对象加入到组件的更新队列中。React 会调度一次更新(reconciliation),在调度过程中,Re…...
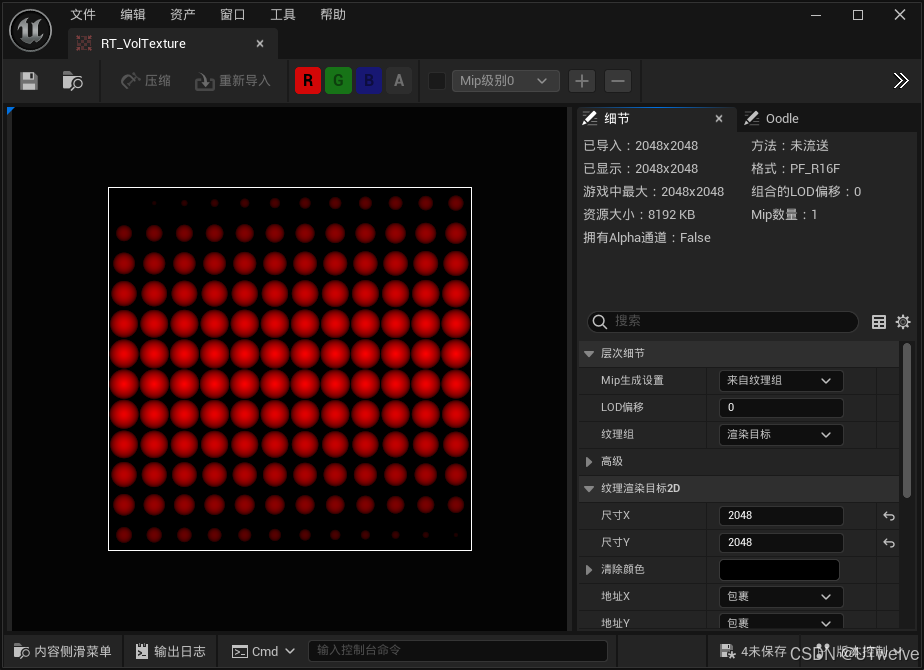
【UE5】将2D切片图渲染为体积纹理,最终实现使用RT实时绘制体积纹理【第七篇-体积纹理绘制】
我们前几篇已经完成了渲染部分,现在终于开始做动态绘制功能了 之前使用的是这样一个体积雾的切片图,那么现在要做的就是动态编辑它 首先,让我们简单了解一下它是如何运作的: 开始绘制画布以渲染目标,并将材质绘制到画…...

Linux的环境搭建
目录 1、linux的简单介绍 2、搭建linux环境 2.1 linux的环境安装 2.2 使用Xshell远程登入linux 2.2.1 Xshell免密登入 2.3 windows与Xshell与linux云服务器的关系 1、linux的简单介绍 linux操作系统 为 部分汇编 C语言编写 的操作系统 源代码公开(开源),官…...

WPF+Mvvm案例实战(五)- 自定义雷达图实现
文章目录 1、项目准备1、创建文件2、用户控件库 2、功能实现1、用户控件库1、控件样式实现2、数据模型实现 2、应用程序代码实现1.UI层代码实现2、数据后台代码实现3、主界面菜单添加1、后台按钮方法改造:2、按钮添加:3、依赖注入 3、运行效果4、源代码获…...

网络爬虫-Python网络爬虫和C#网络爬虫
爬虫是一种从互联网抓取数据信息的自动化程序,通过 HTTP 协议向网站发送请求,获取网页内容,并通过分析网页内容来抓取和存储网页数据。爬虫可以在抓取过程中进行各种异常处理、错误重试等操作,确保爬取持续高效地运行 1、Python网…...

如何有效解除TikTok账号间的IP关联
在当今社交媒体环境中,TikTok凭借其独特的短视频形式吸引了数以亿计的用户。对许多内容创作者而言,运营多个账号是获取更大曝光和丰富内容的有效策略。然而,如何避免这些账号之间的IP关联,以防止被平台识别并封禁,成为…...

Python自省机制
Python 自省机制 Python 自省(Introspection)是一种动态检查对象的能力,使得开发者可以在运行时获取对象的相关信息,比如属性、方法、类型等。自省机制让 Python 具备了更强的动态性和灵活性,便于调试和开发。 自省&…...

wgan-gp 对连续变量 训练,6万条数据,训练结果不错,但是到局部的时候,拟合不好,是否可以对局部数据也进行计算呢
Wasserstein GAN with Gradient Penalty (WGAN-GP) 是一种改进的生成对抗网络(GAN),它通过引入梯度惩罚来改进训练过程,从而提高生成模型的稳定性和质量。如果你在使用WGAN-GP对连续变量进行训练时,发现整体训练结果不…...

python 制作 发货单 (生成 html, pdf)
起因, 目的: 某个小店,想做个发货单。 过程: 先写一个 html 模板。准备数据, 一般是从数据库读取,也可以是 json 格式,或是 python 字典。总之,是数据内容。使用 jinja2 来渲染模板。最终的结果可以是 h…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
