leetcode刷题笔记——15.三数之和
一、问题描述
给定一个整数数组 nums,判断是否存在三元组 [nums[i], nums[j], nums[k]],使得:
-
i != j、i != k且j != k -
nums[i] + nums[j] + nums[k] == 0
需要返回所有和为 0 的三元组,且这些三元组不能重复。
输入输出
-
输入: 整数数组
nums -
输出: 包含所有和为 0 的不重复三元组的列表
示例
-
输入:
nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:存在两个不同的三元组,它们的和均为 0。 -
输入:
nums = [0,1,1]
输出:[]
解释:不存在三元组的和为 0。 -
输入:
nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一的三元组和为 0。
注意事项
-
输出的顺序和三元组内部的顺序不重要。
-
需确保返回的三元组不重复。
二、解题思路以及代码实现
方法 1: 排序 + 双指针法
解题思路
-
排序: 首先对输入数组进行排序。这是因为在有序数组中,可以使用双指针法更有效地查找三元组。
-
遍历数组: 使用一个
for循环遍历每个元素nums[i],确保nums[i]是当前处理的元素(避免重复)。如果nums[i]大于 0,由于数组是有序的,后面的数都将更大,所以可以结束循环。 -
双指针: 对于每个选定的
nums[i],设置两个指针:left指向i+1,right指向数组末尾。计算三数之和current_sum = nums[i] + nums[left] + nums[right]。-
如果
current_sum为 0,保存该三元组,并移动left和right指针,跳过重复的元素。 -
如果
current_sum小于 0,移动left指针向右。 -
如果
current_sum大于 0,移动right指针向左。
-
时间复杂度
-
排序: O(n log n)排序不管是分治排序还是快排的时间复杂度都是 O(n log n),详细可以搜搜
-
双指针遍历: O(n²)
-
总时间复杂度: O(n log n + n²) = O(n²)
空间复杂度
-
O(k),其中 k 是输出中三元组的数量(额外空间用于结果存储)。
代码实现
def threeSum(self, nums: List[int]) -> List[List[int]]:nums.sort() # 排序result = []n = len(nums)for i in range(n):if i > 0 and nums[i] == nums[i - 1]: # 跳过重复元素continueleft, right = i + 1, n - 1while left < right:current_sum = nums[i] + nums[left] + nums[right]if current_sum == 0:result.append([nums[i], nums[left], nums[right]])# 跳过重复元素while left < right and nums[left] == nums[left + 1]:left += 1while left < right and nums[right] == nums[right - 1]:right -= 1left += 1right -= 1elif current_sum < 0:left += 1else:right -= 1 return result方法 2: 哈希表法
解题思路
-
使用哈希表: 利用一个哈希集合来存储每个元素,帮助快速查找。
-
遍历: 对于数组中的每个元素
nums[i],需要找到另外两个数nums[j]和nums[k],使得nums[i] + nums[j] + nums[k] = 0。这可以转化为寻找-nums[i] = nums[j] + nums[k]。 -
双重循环: 使用双重循环遍历数组中的所有可能的组合,计算
target = -nums[i],然后检查哈希表中是否存在可以与nums[j]组合成target的元素nums[k]。 -
避免重复: 使用一个集合存储找到的三元组,确保输出中不包含重复的三元组。
时间复杂度
-
外层循环: O(n),内层循环: O(n)
-
哈希表查找: O(1)
-
总时间复杂度: O(n²)
空间复杂度
-
O(n),用于存储哈希表和结果集合。
代码实现
def threeSum(nums):result = set()n = len(nums)for i in range(n):target = -nums[i]seen = set()for j in range(i + 1, n):complement = target - nums[j]if complement in seen:result.add((nums[i], nums[j], complement))seen.add(nums[j])return [list(triplet) for triplet in result]相关文章:

leetcode刷题笔记——15.三数之和
一、问题描述 给定一个整数数组 nums,判断是否存在三元组 [nums[i], nums[j], nums[k]],使得: i ! j、i ! k 且 j ! k nums[i] nums[j] nums[k] 0 需要返回所有和为 0 的三元组,且这些三元组不能重复。 输入输出 输入: 整…...

NLTK无法下载?
以下内容仅为当前认识,可能有不足之处,欢迎讨论! 文章目录 nltk无法下载怎么办?什么是NLTK?为什么要用NLTK?如何下载? nltk无法下载怎么办? 什么是NLTK? NLTK是学习自然…...
)
采用非递归快排实现找出数组中的前k个高频元素(python)
前k个高频元素 题目描述解题思路代码实现 题目描述 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 输入: nums [1,1,1,2,2,3], k 2 输出: [1,2] 解题思路 (1)先对给定的列表进行…...

Java题集练习4
Java题集练习4 1 异常有什么用? 用来找到代码中产生的错误 防止运行出错2 异常在java中以什么形式存在? 异常在java中以类的形式存在,分为运行时异常和编译期异常,他们都在类Exception中3 异常是否可以自定义?如何自…...

sql进阶篇
1.更新记录 AC: update examination_info set tag replace(tag, "PYTHON", "Python") where tag "PYTHON";2.删除记录 AC: DELETE FROM exam_record WHERE timestampdiff(minute, start_time, submit_time) < 5AND…...

代码工艺:SQL 优化的细节
1. 巧用 limit 当出现深分页的时候,例如: select id, name, status, detail from product limit 100000, 30; 那么MySQL的执行方式为:一共需要查100030条数据,然后丢弃前面的100000条,只返回后面的30条数据…...

天池蚂蚁AFAC大模型挑战赛-冠军方案(含代码)
天池-蚂蚁AFAC大模型挑战赛-冠军方案 前言 ❝ 作者 彭欣怡 华东师大; 马千里 虾皮; 戎妍 港科广 说在前面 在当今信息技术迅猛发展的背景下,大模型技术已经成为推动人工智能领域进步的重要力量。 前段时间备受瞩目的AFAC赛题聚焦于金融对话…...

[QUIC] Packets 和 Frames 概述
Packets 和 Frames 概述 受保护的数据包 (Protected Packets) 基于不同的包类型, QUIC 使用不同等级的保护机制. Version Negotoation 包不受保护. Retry 包使用 AEAD 进行保护。 Initial 包使用 AEAD 进行保护, 但是使用的 Key 是由一个网络可见的值计算出来的。 因此 Ini…...

QT编辑框带行号
很可惜,qt的几个编辑框并没有相关功能。所以我们要自己实现一个。 先讲讲原理: QPlainTextEdit继承自QAbstractScrollArea,编辑发生在其viewport()的边距内。我们可以通过将视口的左边缘设置一个空白区域,…...

Kafka认证时Successfully logged in真的认证成功了?
背景 某个应用需要配置 Kafka 集群信息,且需要在验证集群是否可达。基本实现思路是创建一个生产者对象,然后发送一条测试数据,调用 Producer 的 send 方法发送消息后,再调用 get() 方法,即同步发送消息,测…...

软考信息系统管理师,系统集成项目管理工程师,考哪一个合适?
根据2024年的考试安排,高级项目管理师和系统集成工程师考试改为每年一次。 2024年上半年考高级项目管理师,下半年考系统集成项目管理工程师。 根据这个调整,建议先报名5月份的高级项目管理师考试。如果通过了,大家都高兴&#x…...
)
AI学习指南自然语言处理篇-位置编码(Positional Encoding)
AI学习指南自然语言处理篇-位置编码(Positional Encoding) 目录 引言位置编码的作用位置编码的原理绝对位置编码相对位置编码位置编码在Transformer中的应用位置编码的意义总结 引言 在自然语言处理中,文本数据通常以序列的形式存在。然而…...

macOS 15 Sequoia dmg格式转用于虚拟机的iso格式教程
想要把dmg格式转成iso格式,然后能在虚拟机上用,最起码新版的macOS镜像是不能用UltraISO,dmg2iso这种软件了,你直接转放到VMware里绝对读不出来,办法就是,在Mac系统中转换为cdr,然后再转成iso&am…...

【01初识】-初识 RabbitMQ
目录 学习背景1- 初识 MQ1-1 同步调用什么是同步调用?小结:同步调用优缺点 1-2 异步调用什么是异步调用?小结:异步调用的优缺点,什么时候使用异步调用? 1-3 MQ 技术选型 学习背景 异步通讯的特点ÿ…...

CTF-RE 从0到N:汇编层函数调用
windows 在 Windows 平台上的汇编语言中,调用函数的方式通常遵循特定的调用约定(Calling Convention)。最常见的调用约定包括: cdecl: C 默认调用约定,调用者清理堆栈。stdcall: Windows API 默认调用约定࿰…...

雷池社区版compose配置文件解析-mgt
在现代网络安全中,选择合适的 Web 应用防火墙至关重要。雷池(SafeLine)社区版免费切好用。为网站提供全面的保护,帮助网站抵御各种网络攻击。 compose.yml 文件是 Docker Compose 的核心文件,用于定义和管理多个 Dock…...
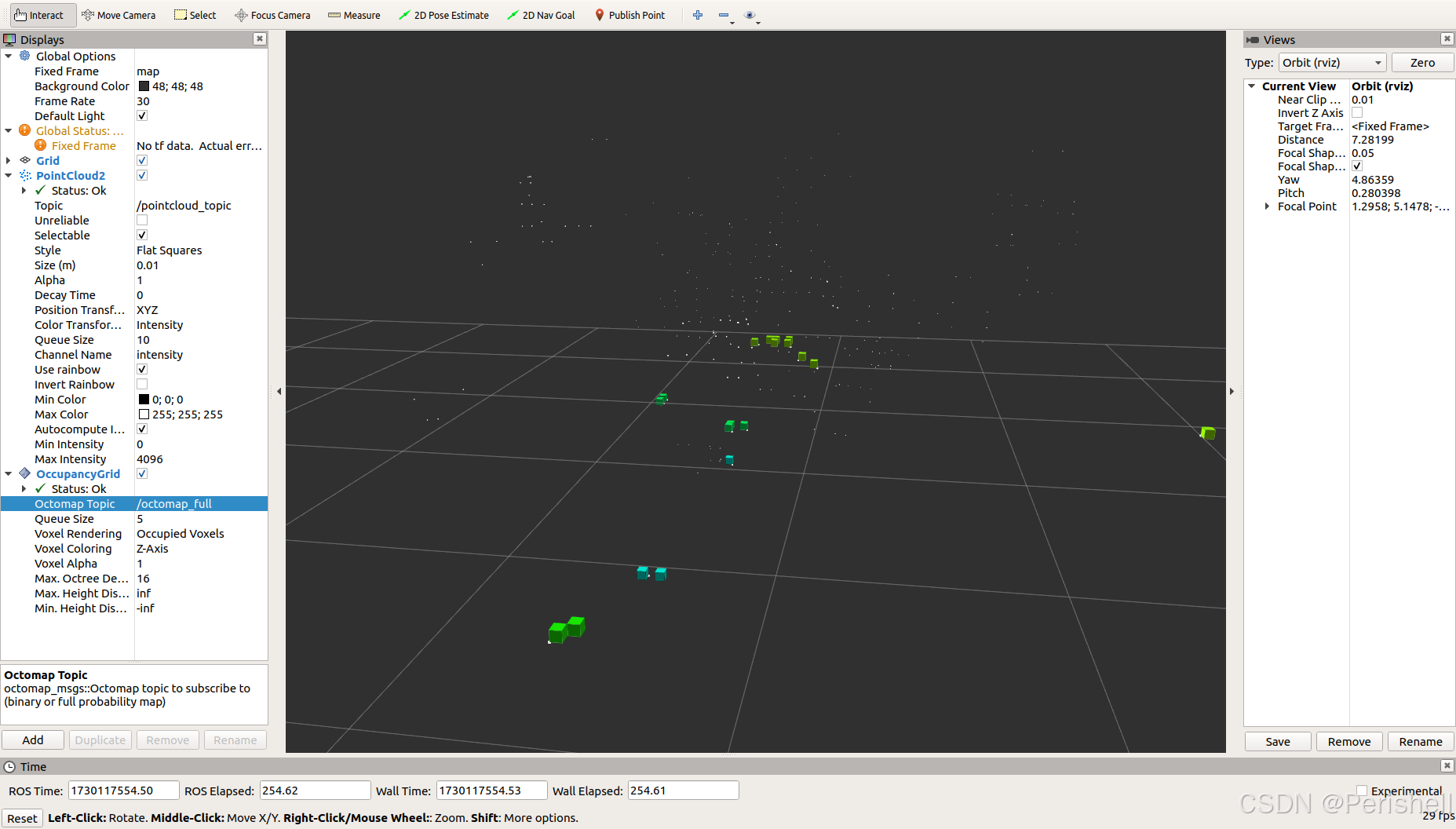
无人机避障——4D毫米波雷达Octomap从点云建立三维栅格地图
Octomap安装 sudo apt-get install ros-melodic-octomap-ros sudo apt-get install ros-melodic-octomap-msgs sudo apt-get install ros-melodic-octomap-server sudo apt-get install ros-melodic-octomap-rviz-plugins # map_server安装 sudo apt-get install ros-melodic-…...

Python(数据结构2)
常见数据结构 队列 队列(Queue),它是一种运算受限的线性表,先进先出(FIFO First In First Out) Python标准库中的queue模块提供了多种队列实现,包括普通队列、双端队列、优先队列等。 1 普通队列 queue.Queue 是 Python 标准库 queue 模块中的一个类…...
深入解析HTTP与HTTPS的区别及实现原理
文章目录 引言HTTP协议基础HTTP响应 HTTPS协议SSL/TLS协议 总结参考资料 引言 HTTP(HyperText Transfer Protocol)超文本传输协议是用于从Web服务器传输超文本到本地浏览器的主要协议。随着网络安全意识的提高,HTTPS(HTTP Secure…...

Java IO 模型
I/O 何为 I/O? I/O(Input/Output) 即输入/输出 。 我们先从计算机结构的角度来解读一下 I/O。 根据冯.诺依曼结构,计算机结构分为 5 大部分:运算器、控制器、存储器、输入设备、输出设备。 输入设备(比…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...
