拓扑学与DNA双螺旋结构的奇妙连接:从算法到分子模拟
拓扑的形变指的是通过连续地拉伸、弯曲或扭曲物体而不进行撕裂或粘合来改变其形状的一种数学变换。拓扑形变属于拓扑学的一个分支,研究在这些操作下保持不变的性质。简单来说,它关注的是物体“形状的本质”,而不是具体的几何形状。
拓扑形变的原理
拓扑学中的形变可视为对象在“同胚”意义下的等价性。同胚是指两个对象可以通过连续的双向变换互相映射,保持空间的连通性和孔洞结构。例如,在拓扑学上,咖啡杯和甜甜圈是等价的,因为可以通过连续形变将一个变为另一个,而不破坏其“环形孔”的结构。
拓扑形变的用途
拓扑学的形变原理可用于以下几个方面:
-
物理模拟:拓扑形变常用于物理学、材料科学等领域,用于模拟物体在不同应力下的变形情况,帮助研究物体的弹性或变形机制。
-
计算机图形学:在3D建模和动画中,拓扑变换用于物体形状变换、软体物体的模拟、模型的动态变形等,使得模型更加逼真。
-
机器人路径规划:拓扑学可以用来分析和规划复杂路径,帮助机器人在特定环境中避免障碍物。
-
数据科学和网络分析:拓扑数据分析(TDA)利用拓扑形变来发现数据集的“形状结构”,可以处理高维数据或非线性结构的数据。
代码示例:简单拓扑形变模拟
以下是一个使用Python和Matplotlib库模拟简单拓扑形变的示例代码。此代码展示了将一个圆形变成一个椭圆形的过程,通过改变每个点的位置来模拟形变。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation# 设置初始圆的点
theta = np.linspace(0, 2 * np.pi, 100)
x = np.cos(theta)
y = np.sin(theta)fig, ax = plt.subplots()
line, = ax.plot(x, y, color='b', lw=2)
ax.set_aspect('equal')
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)# 变换函数:将圆逐渐拉伸为椭圆
def update(frame):# 每帧增加一个变形比例scale = 1 + 0.01 * framenew_x = x * scaleline.set_data(new_x, y)return line,# 使用动画展示变形
ani = FuncAnimation(fig, update, frames=np.arange(0, 100), interval=50)
plt.show()
代码解读
- 初始形状:创建一个圆形,通过点的极坐标表示。
- 变换:通过变换系数
scale逐渐增大,将圆形拉伸为椭圆。 - 动画展示:使用
FuncAnimation连续更新图形以展示拓扑形变。
拓扑形变的实际应用
以上代码展示了一个基础的拓扑形变,但在实际应用中,可以将形变原理应用于更多复杂的系统:
- 在3D模型中应用形变模拟真实物体的扭曲和弯曲。
- 在数据分析中应用拓扑数据分析(TDA)发现数据模式和群体结构。
- 在机器人路径规划中,通过拓扑学避免障碍物检测的计算复杂性。
拓扑形变的思想从简单的二维形变到高维空间的应用,提供了一种不同于传统几何的方法,用于发现和分析复杂系统中的结构特性。
DNA链条的模拟
DNA链条结构可以用拓扑学的概念来研究。DNA的双螺旋结构会因扭转和缠绕产生复杂的拓扑形变,比如形成环、打结、缠绕等。拓扑学在DNA研究中的应用包括分析DNA在复制、转录等过程中的拓扑变化,了解其在扭转、缠绕下的稳定性。这在分子生物学中属于DNA拓扑学。
用代码模拟DNA的拓扑结构,可以生成DNA链条的双螺旋形状,并引入“拓扑形变”,比如扭转或缠绕。以下代码模拟了一个基本的DNA双螺旋,并逐步演示其在扭转过程中的变化。
DNA双螺旋结构模拟代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation# 设置DNA链的参数
n_turns = 5 # 螺旋的圈数
points_per_turn = 100 # 每圈的点数
length = n_turns * points_per_turn # 总点数# 生成双螺旋
theta = np.linspace(0, 2 * np.pi * n_turns, length)
x1 = np.cos(theta)
y1 = np.sin(theta)
z1 = np.linspace(0, 10, length) # DNA链的长度方向# 另一条链,偏移一定距离
x2 = np.cos(theta + np.pi)
y2 = np.sin(theta + np.pi)
z2 = z1 # 同样的长度方向# 初始化图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
line1, = ax.plot([], [], [], color='blue', lw=1.5, label="链 1")
line2, = ax.plot([], [], [], color='red', lw=1.5, label="链 2")
ax.legend()ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(0, 10)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")# 变形函数
def update(frame):# 扭曲参数,用来模拟拓扑形变twist_factor = 0.1 * frame# 新的扭曲形状twisted_x1 = np.cos(theta + twist_factor * z1)twisted_y1 = np.sin(theta + twist_factor * z1)twisted_x2 = np.cos(theta + np.pi + twist_factor * z2)twisted_y2 = np.sin(theta + np.pi + twist_factor * z2)# 更新双螺旋的位置line1.set_data(twisted_x1, twisted_y1)line1.set_3d_properties(z1)line2.set_data(twisted_x2, twisted_y2)line2.set_3d_properties(z2)return line1, line2# 动画
ani = FuncAnimation(fig, update, frames=range(50), interval=100)
plt.show()
代码解读
-
初始双螺旋结构:
- 用参数方程生成两个螺旋线条,代表DNA的两条链。
- 每条链的坐标由角度
theta控制,用不同的相位来使其在空间中对称。
-
拓扑形变:
- 通过增加扭曲因子
twist_factor使双螺旋产生逐步扭曲,模拟DNA在细胞中受到外力后的拓扑形变。 - 这种变形可以模拟DNA在扭转、缠绕等过程中的形态变化,帮助研究其在特定环境下的结构稳定性。
- 通过增加扭曲因子
拓扑形变在DNA研究中的应用
在分子生物学中,拓扑学帮助科学家们理解DNA的折叠、扭曲、打结等行为。例如,拓扑异构酶(一种酶)在细胞中负责切割、旋转和重新连接DNA,使其解开或重新缠绕。通过模拟这些拓扑形变,可以帮助研究DNA在细胞活动过程中的物理特性、酶解机制以及药物靶点等。
如果你觉得这篇文章对你有帮助,不妨点个「赞」支持一下,收藏以便日后参考,也欢迎留言分享你的看法!记得关注,带你解锁更多有趣内容!感谢你的支持,期待与你在下一篇相见!🙏
相关文章:

拓扑学与DNA双螺旋结构的奇妙连接:从算法到分子模拟
拓扑的形变指的是通过连续地拉伸、弯曲或扭曲物体而不进行撕裂或粘合来改变其形状的一种数学变换。拓扑形变属于拓扑学的一个分支,研究在这些操作下保持不变的性质。简单来说,它关注的是物体“形状的本质”,而不是具体的几何形状。 拓扑形变…...
单表查询)
mysql数据库(四)单表查询
单表查询 文章目录 单表查询一、单表查询1.1 简单查询1.2where1.3group by1.4having1.5order by1.6limit 一、单表查询 记录的查询语法如下: SELECT DISTINCT(去重) 字段1,字段2… FROM 表名 WHERE 筛选条件 GROUP BY 分组 HAVING 分组筛选 ORDER BY 排序 LIMIT 限…...
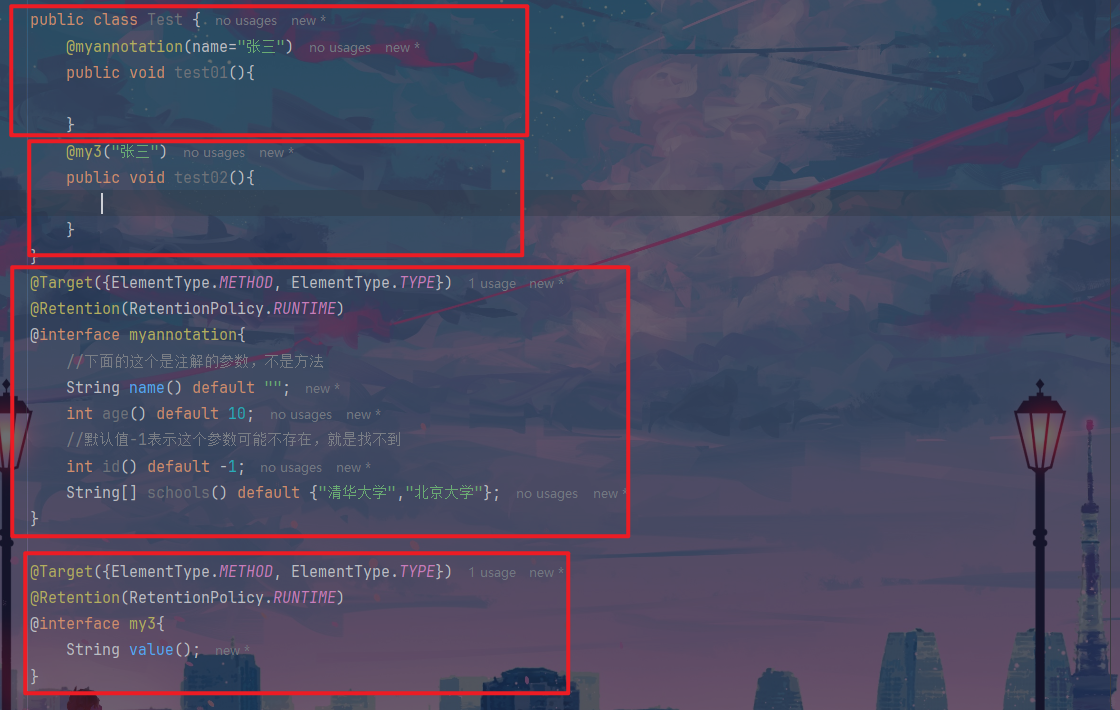
JavaEE初阶---properties类+反射+注解
文章目录 1.配置文件properities2.快速上手3.常见方法3.1读取配置文件3.2获取k-v值3.3修改k-v值3.4unicode的说明 4.反射的引入4.1传统写法4.2反射的写法(初识)4.3反射的介绍4.4获得class类的方法4.5所有类型的class对象4.6类加载过程4.7类初始化的过程4…...

HarmonyOS一次开发多端部署三巨头之功能级一多开发和工程级一多开发
功能级一多开发与工程级一多开发 引言功能级一多开发SysCaps机制介绍能力集canlUse接口 工程级一多开发三层架构规范 引言 一次开发多端部署 定义:一套代码工程,一次开发上架,多端按需部署 目标:支撑开发者快速高效的开发多终端设…...

STL常用遍历算法
概述: 算法主要是由头文件<algorithm> <functional> <numeric>组成。 <algorithm>是所有STL头文件中最大的一个,范围涉及到比较、 交换、查找、遍历操作、复制、修改等等 <numeric>体积很小,只包括几个在序列上面进行简…...

前端开发中常见的ES6技术细节分享一
var、let、const之间有什么区别? var: 在ES5中,顶层对象的属性和全局变量是等价的,用var声明的变量既是全局变量,也是顶层变量 注意:顶层对象,在浏览器环境指的是window对象,在 Node 指的是g…...

行业类别-智慧城市-子类别智能交通-细分类别自动驾驶技术-应用场景城市公共交通优化
1.大纲分析 针对题目“8.0 行业类别-智慧城市-子类别智能交通-细分类别自动驾驶技术-应用场景城市公共交通优化”的大纲分析,可以从以下几个方面进行展开: 一、引言 简述智慧城市的概念及其重要性。强调智能交通在智慧城市中的核心地位。引出自动驾驶…...

[High Speed Serial ] Xilinx
Xilinx 高速串行数据接口 收发器产品涵盖了当今高速协议的方方面面。GTH 和 GTY 收发器提供要求苛刻的光互连所需的低抖动,并具有世界一流的自适应均衡功能,具有困难的背板操作所需的 PCS 功能。 Versal™ GTY (32.75Gb/s)&…...

Unity学习笔记(3):场景绘制和叠层设置 Tilemap
文章目录 前言开发环境规则瓦片绘制拐角 动态瓦片总结 前言 这里学一下后面的场景绘制和叠层技巧。 开发环境 Unity 6windows 11vs studio 2022Unity2022.2 最新教程《勇士传说》入门到进阶|4K:https://www.bilibili.com/video/BV1mL411o77x/?spm_id_from333.10…...

不吹不黑,客观理性深入讨论中国信创现状
1. 题记: 随着美国大选尘埃落定,特朗普当选美国新一任总统,参考他之前对中国政策的风格,个人预计他将进一步限制中国半导体产业和信创产业的发展。本篇博文不吹不黑,客观理性深入探讨中国信创现状。文中数据来自权威媒…...
NoSQL数据库的基本原理)
NoSQL大数据存储技术测试(2)NoSQL数据库的基本原理
写在前面:未完成测试的同学,请先完成测试,此博文供大家复习使用,(我的答案)均为正确答案,大家可以放心复习 单项选择题 第1题 NoSQL的主要存储模式不包括 键值对存储模式 列存储模式 文件…...

「QT」几何数据类 之 QPoint 整型点类
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid…...

植物明星大乱斗5
能帮到你的话,就给个赞吧 😘 文章目录 timer.htimer.cppcamera.hcamera.cppmenuScene.cpp timer.h #pragma once #include <functional>class Timer {public:void reStart();void setTimer(int timerMs);void setIsOneShot(bool isOneShot);void …...

每日算法练习
各位小伙伴们大家好,今天给大家带来几道算法题。 题目一 算法分析 首先,我们应该知道什么是完全二叉树:若一颗二叉树深度为n,那么前n-1层是满二叉树,只有最后一层不确定。 给定我们一棵完全二叉树,我们查看…...

把握鸿蒙生态崛起机遇:开发者如何在全场景操作系统中脱颖而出
把握鸿蒙生态崛起机遇:开发者如何在全场景操作系统中脱颖而出 随着鸿蒙系统的逐步成熟和生态体系的扩展,其与安卓、iOS 形成了全新竞争格局,为智能手机、穿戴设备、车载系统和智能家居等领域带来了广阔的应用前景。作为开发者,如…...

字符串类型排序,通过枚举进行单个维度多个维度排序
字符串类型进行排序通过定义枚举值实现 1.首先创建一个测试类,并实现main方法 2.如果是单个维度的排序,则按照顺序定义一个枚举 public enum Risk {高风险,中风险,一般风险,低风险 } public static void main(String[] args) { }3.main方法里实现如下…...

figma的drop shadow x:0 y:4 blur:6 spread:0 如何写成css样式
figma的drop shadow x:0 y:4 blur:6 spread:0 如何写成css样式 在CSS中,我们可以使用box-shadow属性来模拟Figma中的Drop Shadow效果。box-shadow属性接受的值分别是:横向偏移、纵向偏移、模糊半径、扩展半径和颜色。 但是,Figma的Drop Sha…...

基于Matlab 疲劳驾驶检测
Matlab 疲劳驾驶检测 课题介绍 该课题为基于眼部和嘴部的疲劳驾驶检测。带有一个人机交互界面GUI,通过输入视频,分帧,定位眼睛和嘴巴,通过眼睛和嘴巴的张合度,来判别是否疲劳。 二、操作步骤 第一步:最…...

Linux内核.之 init文件,/init/main.c
想要熟悉内核,看下源码,就非常清晰 Linux内核,head.s,汇编启动cpu相关设置后,启动init文件里的,文件在内核的/init/main.c,看下main函数,做了哪些工作 // SPDX-License-Identifier: …...

CentOS系统中查看内网端口映射的多种方法
在网络管理中,了解和控制内网端口映射是至关重要的。本文将为您详细介绍在CentOS系统中查看内网端口映射的多种方法,助您提升网络管理效率。 使用netstat命令查看端口映射 netstat是一个强大的网络诊断工具。要查看当前的端口映射情况,可以在…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...
