每日算法练习
各位小伙伴们大家好,今天给大家带来几道算法题。
题目一

算法分析
首先,我们应该知道什么是完全二叉树:若一颗二叉树深度为n,那么前n-1层是满二叉树,只有最后一层不确定。
给定我们一棵完全二叉树,我们查看其根的右节点的深度,若其深度仅比根的深度小1,那么说明以根的左节点为根的子树是一颗满二叉树,其数量为L=pow(2,n-1)-1。我们要求的节点数量就是L+1(根)+以根的右节点为根的完全二叉树节点数量。如果根的右节点的深度比根的深度小2,那么以根的右子树为根的完全二叉树是一颗满二叉树,其数量为R=pow(2,n-2)-1。我们要求的节点数量就是R+1+以根的左节点为根的完全二叉树节点数量。这是一个很明显的递归,递归出口分为几种情况:只有根,返回1。根只有一个节点,返回2。根为空,返回0。
我们求树的深度时,只要其左子树不为空一直往左走即可。
代码展示
#include<iostream>
#include<cmath>
using namespace std;
struct node{int data;struct node* left;struct node* right;
};
//前序创建完全二叉树
struct node* create(){struct node *head=(struct node*)malloc(sizeof(struct node));int x;cin>>x;if(x==-1){head=NULL;} else{head->data=x;head->left=create();head->right=create();}return head;
}
//打印检验
void printinfo(struct node* head){if(head){printinfo(head->left);cout<<head->data<<" ";printinfo(head->right);}
}
//获得树的深度
int getheight(struct node *head){struct node *p=head;int count=0;while(p){p=p->left;count++;}return count;
}
//获得完全二叉树节点数量
int getsize(struct node* head){if(!head){return 0;}if(!head->left&&!head->right){return 1;}if(!head->left||!head->right){return 2;}int size=getheight(head);int height=getheight(head->right);if(height+1==size){return pow(2,size-1)+getsize(head->right);}else{return pow(2,size-2)+getsize(head->left);}
}
int main(){struct node *head=create();printinfo(head);cout<<endl;int height=getheight(head);cout<<height<<endl;int size=getsize(head);cout<<size;
}题目二

算法分析
我们首先应该知道子序列可以不连续。关于子序列的问题我们都使用动态规划的思想。dp【i】代表以i位置结尾其最长子序列长度。
那么存在公式:当arr【j】>=arr【i】时,dp【i】为1,否则为dp【j】+1。j的范围为0~i-1,我们取其中的最大值。
代码展示
int getmax1(int *arr,int n){int dp[n];for(int i=0;i<n;i++){dp[i]=0;}dp[0]=1;int max;for(int i=1;i<n;i++){max=0;for(int j=0;j<i;j++){if(arr[j]<arr[i]){if(max<dp[j]){max=dp[j];}}}dp[i]=max+1;}max=-1;for(int i=0;i<n;i++){if(max<dp[i]){max=dp[i];}}return max;
}这是最经典的解法,代码时间复杂度为n^2 。下面我给大家带来一种时间复杂度为nlogn的算法。
算法优化
整体思路不变,我们要做的是减少查找开销,也就是第二层循环。如果我们将dp数组变的有序,是不是就可以使用二分查找了呢?
为此,我们引进数组end,end【i】代表递增子序列长度为i+1结尾位置的数字大小。具体思想如下:此时新来了一个数字x,从end数组中找第一个大于x的数字,我们用x取代它即可(递增子序列数字越小说明其扩充的可能性越大)。若没有比它大的数字,我们从end数组中开辟一个新的位置,并且赋值为x(x不能取代任何位置只能新增)。这样最终答案就是i+1了。
其中查找数组中第一个比x大的元素时,我们使用二分查找仅需要logn水平,综合整个代码就是n*logn的。
//寻找有序数组中第一个比x大的元素没有返回-1
int find(int *arr,int n,int x){int left=0,right=n-1,res=-1;int mid;while(left<=right){mid=(left+right)/2;if(arr[mid]<=x){left=mid+1;}else{res=mid;right=mid-1;}}return res;
}
int getmax2(int *arr,int n){int end[n],x,count=0;for(int i=0;i<n;i++){if(i==0){end[count++]=arr[i];continue;}x=find(end,count,arr[i]);if(x==-1){end[count++]=arr[i];}else{end[x]=arr[i];}}return count;
}题目三

算法分析
这道题设计一个知识点:我们求一个数是否可以整除3,可以将其各位相加得到新和再去整除3。即:假设判断123456能否取余3,我们可以根据1+2+3+4+5+6=21能否取余3判断。并且这个知识点是可逆的,我们判断1+2+3+4+5+6也可以判断1+2+3+4+56判断。
这样这道题就很简单了。输入一个n,那么这个数代表1234.....n。我们可以根据1+2+3+4+...+n来判断,直接使用等差数列求和公式求出和即可。
代码展示
#include<iostream>
using namespace std;
int main(){int n;cin>>n;int sum=(1+n)*n/2;string str=sum%3==0?"可以整除":"不能整除"; cout<<str;
}题目四

算法分析
这是一道贪心算法题目:怎么贪呢?如果i位置需要路灯,并且我们发现i+1位置也需要路灯,那我们就放在i+1位置。除此之外还有其它抉择:如果i位置是x,不能放路灯(规定),i++。如果i位置是、并且i+1位置是x,那么需要i位置放路灯,i=i+2。还有一种情况就是i和i+1都是、我们贪心一下,i=i+3。大家也要注意越界。当i位置是、并且i+1越界,那么需要i位置放路灯。
代码展示
#include<iostream>
using namespace std;
int getlight(string s){int count=0,i=0;while(i<s.length()){if(s[i]=='x'){i++;continue;}else{count++;if(i+1==s.length()){cout<<"结尾放路灯"<<endl;break;}else if(s[i+1]=='x'){cout<<"我是.我的后面是x"<<endl;i=i+2;}else if(s[i+1]=='.'){cout<<"我是.我的后面是."<<endl;i=i+3;}}}return count;
}
int main(){string s="x.x...x..x.x...x";int size=getlight(s);cout<<size;
}题目五

算法分析
首先大家要知道为什么没有重复节点,若有重复节点,那么后序遍历结果不唯一。一般关于二叉树的题目,我们都使用递归的方法。
我们知道了先序和中序遍历结果,那么先序的第一个元素就是后序的最后一个元素,我们可以直接填好。然后在中序结果中查找此元素,就可以将先序、中序、后序数组分为左右两部分。然后对左数组进行递归,对右数组进行递归即可。
代码展示
#include<iostream>
using namespace std;
int find(int *arr,int start,int end,int x){for(int i=start;i<=end;i++){if(arr[i]==x){return i;}}
}
void getpos(int *pre,int *in,int *pos,int start1,int end1,int start2,int end2,int start3,int end3){if(start1>end1||start2>end2||start3>end3){return;}if(start1==end1){pos[end3]=pre[start1];return;}pos[end3]=pre[start1];int x=find(in,start2,end2,pre[start1]);getpos(pre,in,pos,start1+1,start1+x-start2,start2,x-1,start3,start3+x-1-start2);//递归左 getpos(pre,in,pos,start1+x+1-start2,end1,x+1,end2,start3+x-start2,end3-1);//递归右
}
int main(){int pre[7]={1,2,4,5,3,6,7};int in[7]={4,2,5,1,6,3,7};int pos[7];getpos(pre,in,pos,0,6,0,6,0,6);for(int i=0;i<7;i++){cout<<pos[i]<<" ";}
}大家注意左右数组的划分,这是重点!!并且我们求左数组长度时:找到了中序遍历中左数组结束位置,注意减去中序遍历开始位置 !!大家不要误认为0!!
题目六

算法分析
根据题目我们就可以知道这是一道前缀树问题,创建好前缀树只需要深搜遍历打印即可。
代码展示
这是前缀树的通用模板。运用到改题目时:只需要在node节点添加一个data数据记录元素即可。最后深搜打印结果即可。
对于深搜不了解的小伙伴们,查看我之前的文章:图(邻接矩阵)知识大杂烩!!(邻接矩阵结构,深搜,广搜,prim算法,kruskal算法,Dijkstra算法,拓扑排序)(学会一文让你彻底搞懂!!)-CSDN博客
#include<iostream>
#include<unordered_set>
using namespace std;
struct node{int pass;int end;struct node* next[26];
};
typedef struct node* Node;
Node create(){Node n=(Node)malloc(sizeof(struct node));n->pass=0;n->end=0;for(int i=0;i<26;i++){n->next[i]=nullptr;}return n;
}
void insert(Node root,string str){Node node=root;int path;for(int i=0;i<str.length();i++){node->pass++;path=str[i]-'a';if(node->next[path]==nullptr){node->next[path]=create();}node=node->next[path];}node->pass++;//最后一个没有加 node->end++;
}
//寻找str出现多少次
int possearch(Node root,string str){Node node=root;int path;for(int i=0;i<str.length();i++){path=str[i]-'a';if(node->next[path]==nullptr){return 0;}node=node->next[path];}return node->end;
}
//寻找以str字符串作为前缀的字符串次数
int presearch(Node root,string str){Node node=root;int path;for(int i=0;i<str.length();i++){path=str[i]-'a';if(node->next[path]==nullptr){return 0;}node=node->next[path];}return node->pass;
}
void deletenode(Node root,string str){if(!possearch(root,str)){cout<<"不存在该字符串无法删除"<<endl;return;}int path;Node node=root;node->pass--;for(int i=0;i<str.length();i++){path=str[i]-'a';if(node->next[path]->pass==1){node->next[path]=nullptr;return;}node=node->next[path]; node->pass--;}node->end--;
}
int main(){Node root=create();string str="abc";insert(root,str);str=str+"d";insert(root,str);deletenode(root,"abc");int findendsize=presearch(root,"abc");cout<<findendsize;
}本期算法分享到此结束!大家多多点赞支持!!
相关文章:

每日算法练习
各位小伙伴们大家好,今天给大家带来几道算法题。 题目一 算法分析 首先,我们应该知道什么是完全二叉树:若一颗二叉树深度为n,那么前n-1层是满二叉树,只有最后一层不确定。 给定我们一棵完全二叉树,我们查看…...

把握鸿蒙生态崛起机遇:开发者如何在全场景操作系统中脱颖而出
把握鸿蒙生态崛起机遇:开发者如何在全场景操作系统中脱颖而出 随着鸿蒙系统的逐步成熟和生态体系的扩展,其与安卓、iOS 形成了全新竞争格局,为智能手机、穿戴设备、车载系统和智能家居等领域带来了广阔的应用前景。作为开发者,如…...

字符串类型排序,通过枚举进行单个维度多个维度排序
字符串类型进行排序通过定义枚举值实现 1.首先创建一个测试类,并实现main方法 2.如果是单个维度的排序,则按照顺序定义一个枚举 public enum Risk {高风险,中风险,一般风险,低风险 } public static void main(String[] args) { }3.main方法里实现如下…...

figma的drop shadow x:0 y:4 blur:6 spread:0 如何写成css样式
figma的drop shadow x:0 y:4 blur:6 spread:0 如何写成css样式 在CSS中,我们可以使用box-shadow属性来模拟Figma中的Drop Shadow效果。box-shadow属性接受的值分别是:横向偏移、纵向偏移、模糊半径、扩展半径和颜色。 但是,Figma的Drop Sha…...

基于Matlab 疲劳驾驶检测
Matlab 疲劳驾驶检测 课题介绍 该课题为基于眼部和嘴部的疲劳驾驶检测。带有一个人机交互界面GUI,通过输入视频,分帧,定位眼睛和嘴巴,通过眼睛和嘴巴的张合度,来判别是否疲劳。 二、操作步骤 第一步:最…...

Linux内核.之 init文件,/init/main.c
想要熟悉内核,看下源码,就非常清晰 Linux内核,head.s,汇编启动cpu相关设置后,启动init文件里的,文件在内核的/init/main.c,看下main函数,做了哪些工作 // SPDX-License-Identifier: …...

CentOS系统中查看内网端口映射的多种方法
在网络管理中,了解和控制内网端口映射是至关重要的。本文将为您详细介绍在CentOS系统中查看内网端口映射的多种方法,助您提升网络管理效率。 使用netstat命令查看端口映射 netstat是一个强大的网络诊断工具。要查看当前的端口映射情况,可以在…...
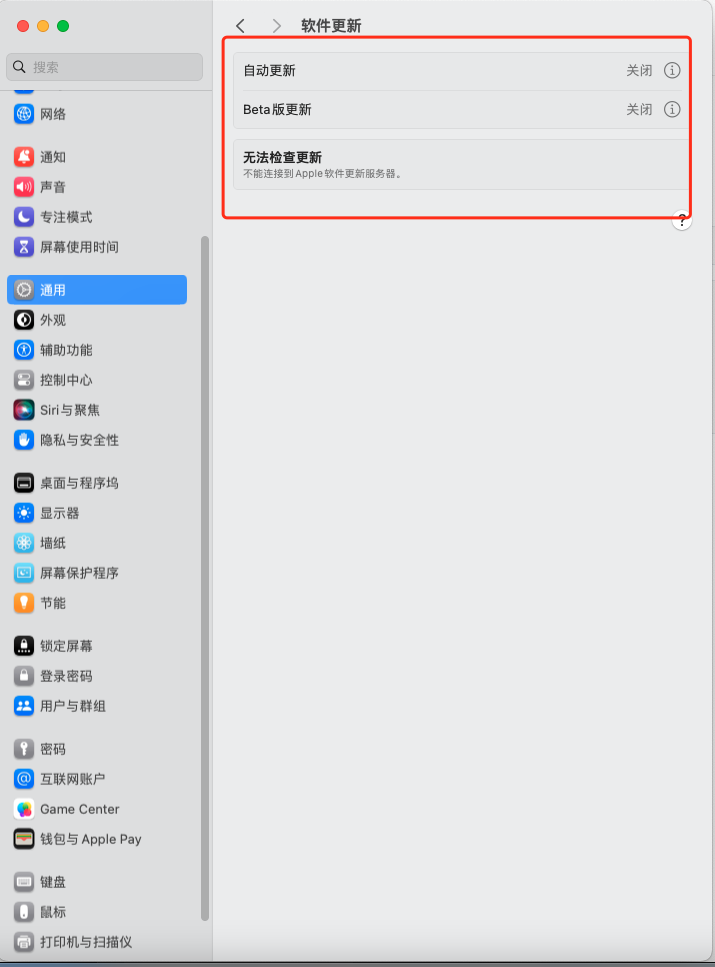
Mac中禁用系统更新
Mac中禁用系统更新 文章目录 Mac中禁用系统更新1. 修改hosts,屏蔽系统更新检测联网1. 去除系统偏好设置--系统更新已有的小红点标记 1. 修改hosts,屏蔽系统更新检测联网 打开终端,执行命令: sudo vim /etc/hosts127.0.0.1 swdis…...

GoogLeNet-水果分类
GoogLeNet-水果分类 1.数据集 官方下载地址:https://www.kaggle.com/datasets/karimabdulnabi/fruit-classification10-class?resourcedownload 备用下载地址:https://www.123684.com/s/xhlWjv-pRAPh 介绍: 十个类别:苹果、…...

深度学习入门指南:一篇文章全解
目录 0.前言 1.深度学习的背景历史 2.深度学习主要研究的内容 3.深度学习的分支 3.1.卷积神经网络(CNN) 3.2 递归神经网络(RNN) 3. 3长短期记忆网络(LSTM) 4.深度学习的主要应用 4.1计算机视觉 4…...

java ssm 医院病房管理系统 医院管理 医疗病房信息管理 源码 jsp
一、项目简介 本项目是一套基于SSM的医院病房管理系统,主要针对计算机相关专业的和需要项目实战练习的Java学习者。 包含:项目源码、数据库脚本、软件工具等。 项目都经过严格调试,确保可以运行! 二、技术实现 后端技术&#x…...

钩子函数的使用
钩子函数在计算机科学和软件工程中,特别是在编程框架和库中,是一种特殊的函数或方法,它们允许用户在框架或库的特定点插入自定义代码。这些钩子提供了一种扩展框架功能而无需修改其源代码的方式。 在前后端分离的项目中,如使用Dj…...

【Docker】自定义网络:实现容器之间通过域名相互通讯
文章目录 一. 默认网络:docker0网络的问题二. 自定义网络三. nginx容器指之间通过主机名进行内部通讯四. redis集群容器(跳过宿主机)内部网络通讯1. 集群描述2. 基于bitnami镜像的环境变量快速构建redis集群 一. 默认网络:docker0…...

护理陪护系统|护理陪护软件|陪护软件
在当今社会,随着人口老龄化的加剧和生活节奏的加快,护理陪护服务的需求日益增长。为了满足这一需求,开发定制一套高效、专业的护理陪护系统显得尤为重要。在开发过程中,有几个关键方面不能忽视。 一、用户需求分析 护理陪护系统的…...

苍穹外卖-账号被锁定怎么办?
刚刚解决的小问题, 最近在搞黑马程序员的苍穹外卖项目, 在完善开发编辑员工功能的时候, 不知道怎么搞的, 无论是swagger接口测试, 还是前后端联调, 都显示"账号被锁定", 原本想在网上找找解释, 结果我太笨, 搜不到, 那就只能在代码里面排查咯, 既然是登录接口出…...

webpack loader全解析,从入门到精通(10)
webpack 的核心功能是分析出各种模块的依赖关系,然后形成资源列表,最终打包生成到指定的文件中。更多复杂的功能需要借助 webpack loaders 和 plugins 来完成。 1. 什么是 Loader Loader 本质上是一个函数,它的作用是将某个源码字符串转换成…...

python机器人Agent编程——实现一个本地大模型和爬虫结合的手机号归属地天气查询Agent
目录 一、前言二、准备工作三、Agent结构四、python模块实现4.1 实现手机号归属地查询工具4.2实现天气查询工具4.3定义创建Agent主体4.4创建聊天界面 五、小结PS.扩展阅读ps1.六自由度机器人相关文章资源ps2.四轴机器相关文章资源ps3.移动小车相关文章资源ps3.wifi小车控制相关…...

【动态规划】斐波那契数列模型总结
一、第 N 个泰波那契数 题目链接: 第 N 个泰波那契数 题目描述: 题目分析: 1、状态表示: dp[i] 表示:第 i 个斐波那契数的值 2、状态转移方程: 由题意可知第 i 个数等于其前三个数之和 dp[i] dp[i-…...

EasyUI弹出框行编辑,通过下拉框实现内容联动
EasyUI弹出框行编辑,通过下拉框实现内容联动 需求 实现用户支付方式配置,当弹出框加载出来的时候,显示用户现有的支付方式,datagrid的第一列为conbobox,下来选择之后实现后面的数据直接填充; 点击新增:新…...
使用 PageOffice 实现word文件在线留痕)
国产linux系统(银河麒麟,统信uos)使用 PageOffice 实现word文件在线留痕
PageOffice 国产版 :支持信创系统,支持银河麒麟V10和统信UOS,支持X86(intel、兆芯、海光等)、ARM(飞腾、鲲鹏、麒麟等)、龙芯(LoogArch)芯片架构。 查看本示例演示效果 …...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
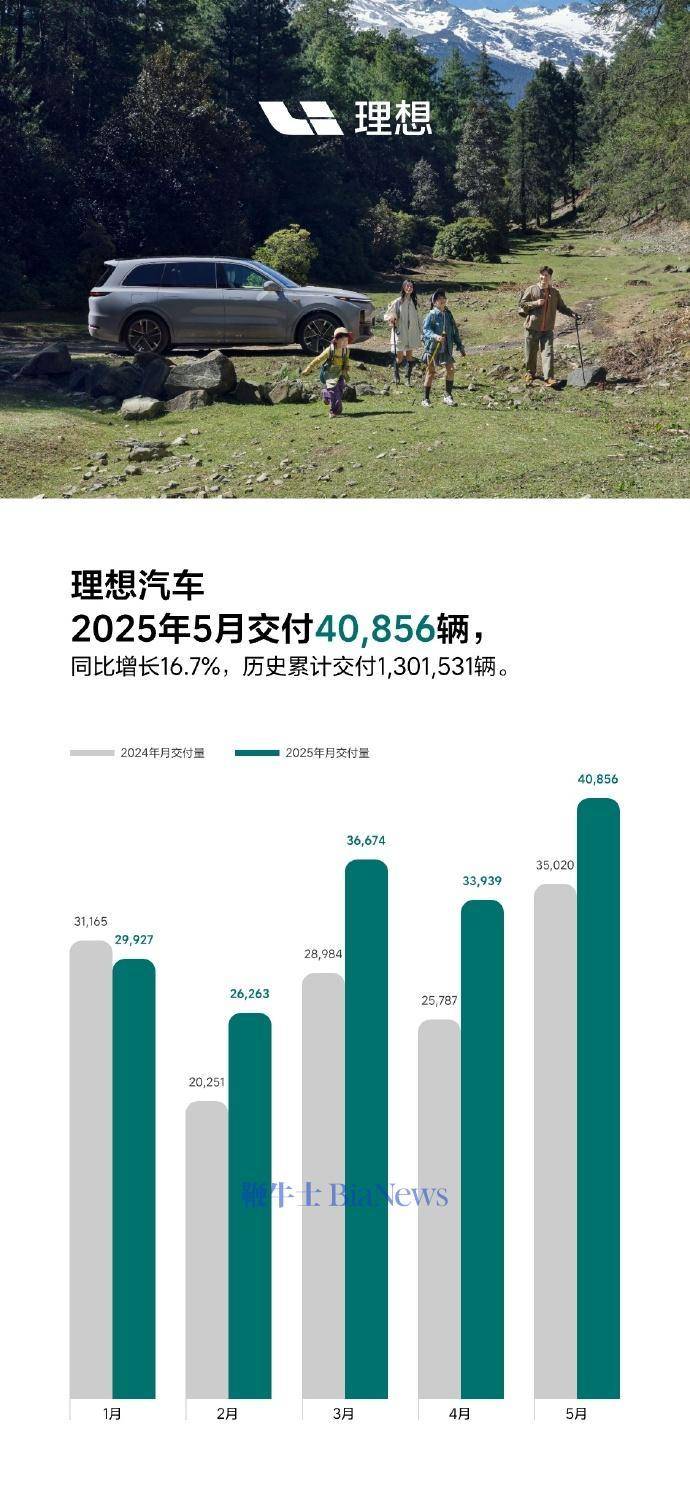
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...

Spring是如何实现无代理对象的循环依赖
无代理对象的循环依赖 什么是循环依赖解决方案实现方式测试验证 引入代理对象的影响创建代理对象问题分析 源码见:mini-spring 什么是循环依赖 循环依赖是指在对象创建过程中,两个或多个对象相互依赖,导致创建过程陷入死循环。以下通过一个简…...
