分类模型评估：混淆矩阵、准确率、召回率、ROC

1. 混淆矩阵

在二分类问题中，混淆矩阵被用来度量模型的准确率。因为在二分类问题中单一样本的预测结果只有Yes or No，即：真或者假两种结果，所以全体样本的经二分类模型处理后，处理结果不外乎四种情况，每种情况都有一个专门称谓，如果用一个2行2列表格描述，得到的就是“混淆矩阵”，以下是遵循sklearn规范的混淆矩阵布局（本文地址：https://laurence.blog.csdn.net/article/details/129006571，转载请注明出处！)：

	预测为’假’	预测为’真’
实际为’假’	真阴性 / TN (True Negative)	假阳性 / FP (False Positive)
实际为’真’	假阴性 / FN (False Negative)	真阳性 / TP (True Positive)

助记：

• 行：实际值，第1行：假，第2行：真；
• 列：预测值，第1列：假，第2列：真
• 主对角线：真阴、真阳，均以T开头
• 副对角线：假阳、假阴，均以F开头

名称	缩写	解释(1)	解释(2)
真阴性	TN	预测为阴，实测也为阴	预测为假，实测也为假
假阳性	FP	预测为阳，实测为阴（错报）	预测为真，实测为假
假阴性	FN	预测为阴，实测为阳（漏报）	预测为假，实测为真
真阳性	TP	预测为阳，实测也为阳	预测为真，实测也为真

其中，假阳性（FP）又被称为“Type 1 Error”，就是“错报”，假阴性（FN）又被称为“Type 2 Error”，就是“漏报”。混淆矩阵的4个值定义清晰，没有任何歧义，容易让人搞混的是混淆矩阵的布局，因为业界没有统一规定过在混淆矩阵中实际值和预测值谁应该是行谁应该是列，也没规定真假值/正负值谁应是第一行谁应是第二行，所以在不同的资料和程序库中就会出现行列结构或顺序相反的情况，所以要特别留意一下混淆矩阵的布局。本文遵循的是sklearn中定义的混淆矩阵结构，使用公式描述就是：

$$ConfusionMatrix=\left[\begin{array}{cc}TN& FP\\ FN& TP\end{array}\right]$$

在《Hands-On ML》一书的第三章，就计算过针对图片（数字5）的二分类模型处理结果的混淆矩阵：

上述案例使用的是MNIST数据集，训练数据6万张图片（使用6万张图片训练，同时再使用它们进行评估），根据红框中的混淆矩阵可知：

• 实际不是数字5，模型预测也不是数字5（预测正确）的图片有：53892张
• 实际不是数字5，模型预测是数字5（预测错误）的图片有：687张
• 实际是数字5，模型预测不是数字5（预测错误）的图片有：1891张
• 实际是数字5，模型预测也是数字5（预测正确）的图片有：3530张

2. 准确率与召回率

在混淆矩阵的四个数据基础之上，人们还设计了两种常用的度量指标，分别是准确率和召回率：

• 准确率 ( Precision )

  在所有“预测为真”（TP+FP）的样本中，有多少是“预测对了”（TP）的? 这个百分比叫准确率 ( Precision )，计算公式：
  $$Precision=\frac{TP}{TP+FP}$$

• 召回率 ( Recall )

  在所有“实际为真”（TP + FN）的样本中，有多少是“预测对了”（TP）的? 这个百分比叫召回率 ( Recall )，计算公式：
  $$Recall=\frac{TP}{TP+FN}$$

在《Hands-On ML》一书的第三章，给出了一张图，清晰明了地阐述了混淆矩阵、准确率、召回率三者之间的关系：

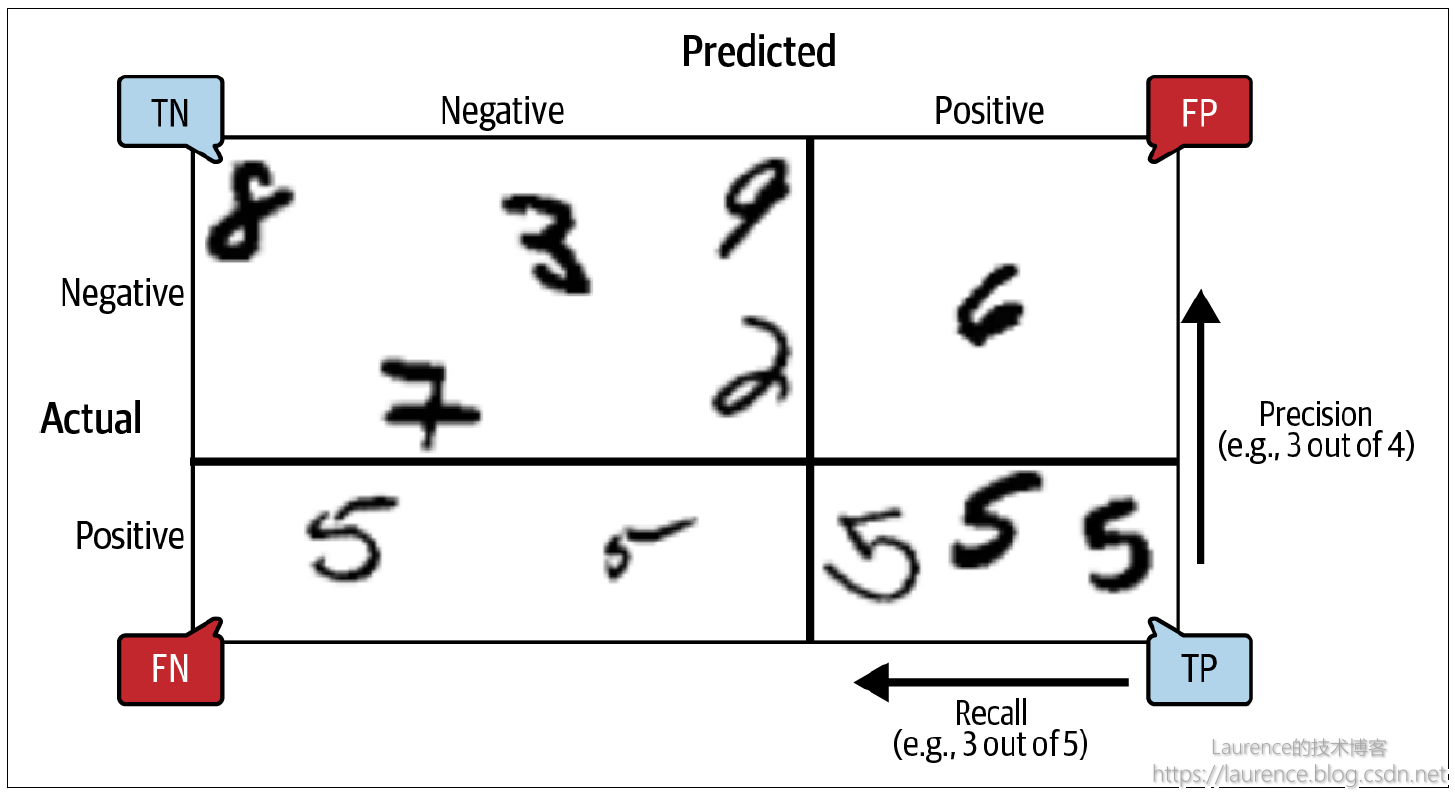
注意：该图4个象限的布局对应Sklearn中的混淆矩阵的布局。网上有的资料介绍混淆矩阵使用的4象限图表
未必与本图一致，它们对于行列是实际值还是预测值的定义可能是反的，对于真假值/正负值谁是第一行谁是二行的定义可能是反的，请一定注意区分！

3. 准确率与召回率之间的权衡

人们之所以会定义“准确率”和“召回率”这两个概念，是因为它们能从两个不同的维度（或者说角度）度量二分类模型的准确性，且在不同的场景里，人们对这两个指标的看重程度是不一样的。引用《Hands-On ML》一书给出的两个例子：

• 案例一: 过滤少儿不宜的视频

  在这个场景中，模型的任务是：判定视频是否适合儿童观看，True表示健康视频，False表示少儿不宜。在该场景下模型应该追求的是：宁可将部分健康视频错误地认定为少儿不宜，也要最大限度地保证认定为健康的视频一定是健康的，这是典型的“优先保证高准确率，允许牺牲一定召回率”的场景。

• 案例二：识别商超监控中的盗窃行为

  在这个场景中，模型的任务是：判定视频中的人是否有盗窃行为，True表示有，False表示无。在该场景下模型应该追求的是：宁可将部分正常行为的视频错误地认定为了盗窃，也要最大限度地保证所有盗窃行为都能被识别出来，这是典型的“优先保证高召回率，允许牺牲一定准确率”的场景。

很多时候，鱼和熊掌不可兼得，在模型调至最优状态时，依然要在“准确率”与“召回率”之间作出“权衡”，它们之间是“此消彼长”的博弈关系，通过调整阈值是可以调节两者的大小的。我们以《Hands-On ML》第三章“识别数字5”的图片二分类结果为例解释的“准确率”与“召回率”之间的“权衡”或者“博弈”关系：

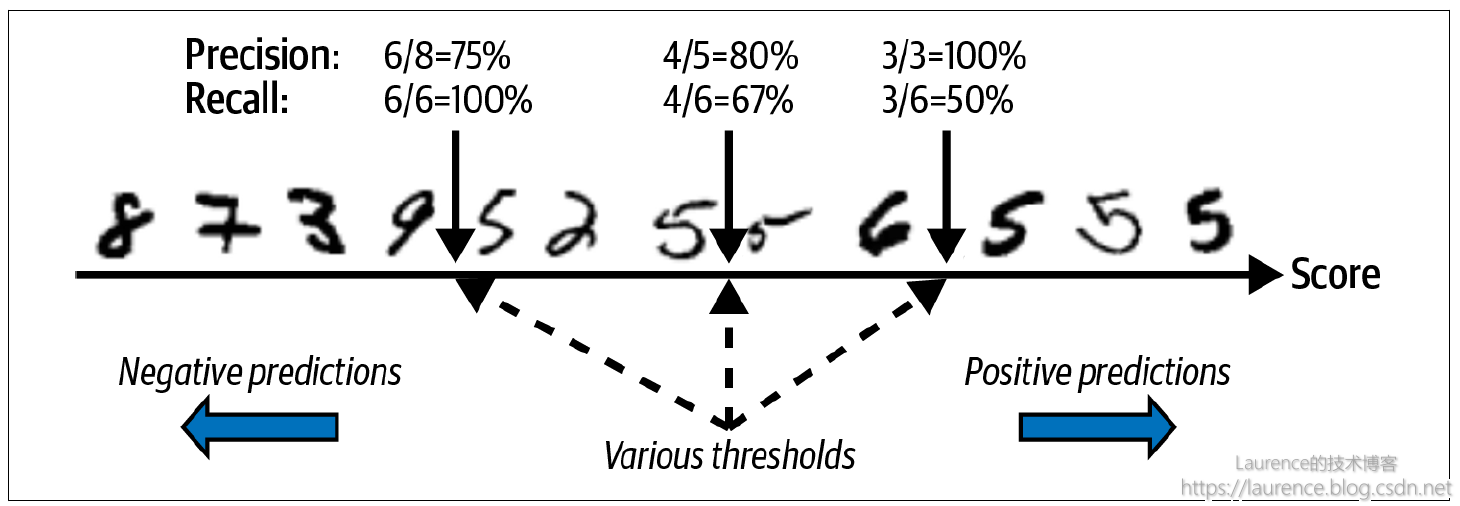
首先，图中12张数字图片的排序不是随机的，而是根据模型给它们的“评分”按从小到大的顺序在Score数轴上依次排列的。这里是“准确率”与“召回率”之间可调的关键，因为虽然二分类模型给出的是一个Yes or No的二元结果，但在模型内部其实为维护的是一个“量值”，通过调节“阈值”的大小，可以决定最终输出的是Yes还是No，这会影响一个“不是很容易分辨的样本”最后被划定成FP还是FN（TP和TN的分值一般会很高或很低，受阈值调整的影响不大，这很容易理解）。以图示的情况为例：

• 情形一：阈值设定在数轴左侧图片9和5的得分之间（暂不考虑具体数值），则右侧8张图片均会被判定为True，8张图片中实际有两个数字2和6被错误判定了，所以准确率=6/8=75%；同时，在总计6张的数字5图片中，该阈值设定下，全部6张数字5的图片都被判定为True，所以召回率=6/6=100%

• 情形二：阈值设定在数轴中间两张图片5的得分之间（暂不考虑具体数值），则右侧5张图片均会被判定为True，5张图片中实际有1个数字6被错误判定了，所以准确率=4/5=80%；同时，在总计6张的数字5图片中，该阈值设定下，只有4张数字5的图片都被判定为True，所以召回率=4/6=67%

• 情形三：阈值设定在在数轴右侧图片6和5的得分之间（暂不考虑具体数值），则右侧3张图片均会被判定为True，3张图片全部正确判定，所以准确率=3/3=100%；同时，在总计6张的数字5图片中，该阈值设定下，只有3张数字5的图片都被判定为True，所以召回率=3/6=50%

从上述三次阈值的调节中我们可以清晰观察到：“准确率”和“召回率”之间此消彼长的博弈关系。

关于上述解释中所说的“评分”，专业名称叫“Confidence Score”，分值越高表示结果为True的可能性越大。在Sklearn中使用SGDClassifier.decision_function(X)方法可以计算出给定样本的评分，下图是书中针对某一个数字5的图片计算score的示例代码:

4. 如何设定期望的准确率与召回率？

就像前面介绍的两个案例一样，不同的情形下，人们对于模型的准确率与召回率的期望是不同的，而通过设定Score的阈值，我们就可以调整模型预测的准确率和召回率。我们可以自行推导一下寻找期望的准确率和召回率组合的方法：

假设有1000个样本，首先，计算出所有样本的Confidence Score，按分值从小到大排好，以每一个score作为阈值，计算对应的准确率和召回率，这样就会得出准确率和召回率伴随阈值变化的曲线，可以想见：当阈值取最小的score时，全部样本都会被判定为True，所以召回率将是100%，而准确率会非常低，而当阈值取到最大的score时，全部样本都会被判定为False，此时召回率将降为0，准确率会趋向于无穷大。为此，Sklearn专门提供了一个函数sklearn.metrics.precision_recall_curve（官方文档）用于计算一组样本+对应成绩的准确率和召回率曲线，下图是《Hands-On ML》一书利用这个函数绘制的数字5的准确率和召回率变化曲线：

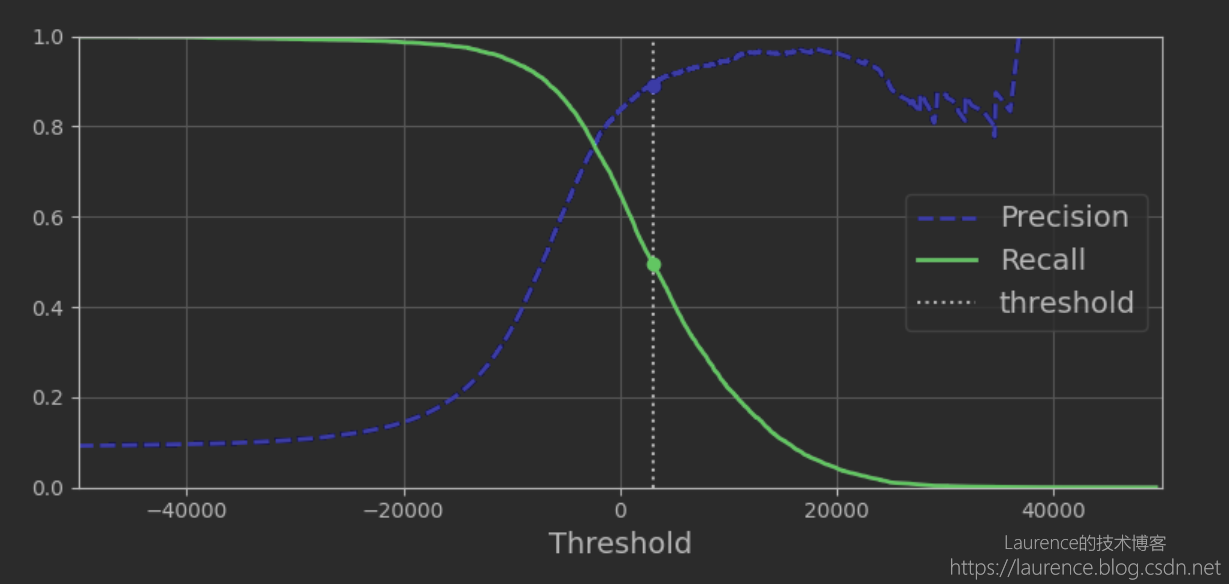
这张图已经把阈值变化对准确率和召回率的影响描述地非常清晰了，从这张图上也能清晰地看出准确率和召回率之间的“此消彼长”的博弈关系。此外，我们还可以观察准确率和召回率之间的变化关系，就是以Recall为横坐标，Precision为纵坐标绘制的曲线，一般称之为Precision-Recall曲线，下图是《Hands-On ML》针对上述准确率和召回率数据绘制的两者变化关系，这张图提供了一些额外的“信息”，我们可以从中发现：一但准确率低于80%以后就会急剧下降，当然，这也意味着召回率是在急剧上升。

假设我们最终选择了：准确率90% + 召回率50% 的组合，接下来的工作就是找出它们所对应的阈值，然后将这个阈值设置给模型产出符合预期的预测结果。但是，这里有一个不问题，那就是：Sklearn其实并不提供修改其内部阈值的接口（不允许用户直接修改），怎么办呢？非常简单，我们只需要拿到score数组，然后和自己设定的threshold值进行矩阵逻辑计算，就可以轻松获得最终的判定结果：布尔数组，就是下面的做法：

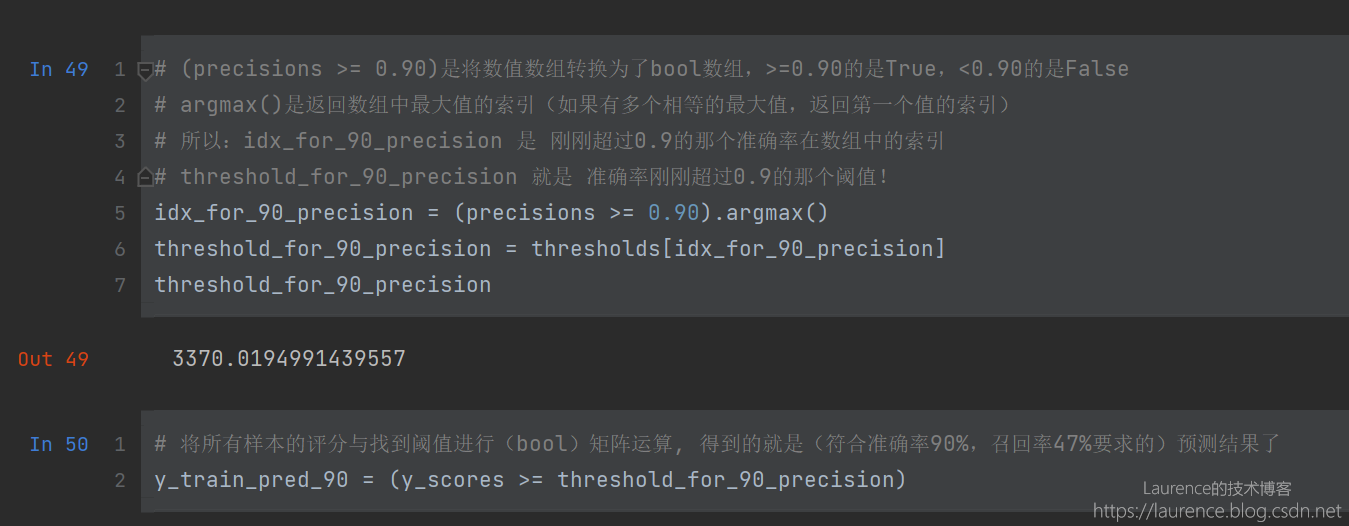
5. ROC

ROC的全称是“受试者工作特征”（Receiver Operating Characteristic）曲线，是另一种评判分类模型结果好坏的一方法。ROC曲线与Precision-Recall曲线类似，也是用两个比值作为横纵坐标绘制的曲线，这两个比值分别是：

• 假阳性率 ( False Positice Rate，FPR )

  在所有“实际为假”（FP+TN）的样本中，有多少是“预测错了”（FP）的? 这个百分比叫假阳性率（FPR），计算公式：
  $$FalsePositiveRate(FPR)=\frac{FP}{FP+TN}$$

• 真阳性率 ( True Positive Rate，TPR )

  在所有“实际为真”（TP + FN）的样本中，有多少是“预测对了”（TP）的? 这个百分比叫真阳性率（TPR），其实也就是召回率（Recall），计算公式：
  $$TruePositiveRate(TPR)=\frac{TP}{TP+FN}$$

而ROC曲线就是以假阳性率（FPR）为横坐标，真阳性率（TPR）为纵坐标绘制的曲线：

其实前面已经介绍过好几种度量分类模型效果的指标了，ROC有什么特别之处呢？

TBD…

6. 概念汇总

• 准确率 ( Precision )

  在所有“预测为真”（TP+FP）的样本中，有多少是“预测对了”（TP）的? 这个百分比叫准确率 ( Precision )，计算公式：
  $$Precision=\frac{TP}{TP+FP}$$

• 召回率 ( Recall )

  在所有“实际为真”（TP + FN）的样本中，有多少是“预测对了”（TP）的? 这个百分比叫召回率 ( Recall )，其实也就是真阳性率 ( True Positive Rate，TPR )，计算公式：
  $$Recall=\frac{TP}{TP+FN}$$

• 真阳性率 ( True Positive Rate，TPR )

  在所有“实际为真”（FN + TP）的样本中，有多少是“预测对了”（TP）的? 这个百分比叫真阳性率（TPR），其实也就是召回率（Recall），计算公式：
  $$TruePositiveRate(TPR)=\frac{TP}{FN+TP}$$

• 真阴性率 ( True Negative Rate，TNR )

  在所有“实际为假”（TN + FP）的样本中，有多少是“预测对了”（TN）的? 这个百分比叫真阴性率（TNR），计算公式：
  $$TrueNegativeRate(TPR)=\frac{TN}{TN+FP}$$

• 假阳性率 ( False Positice Rate，FPR )

  在所有“实际为假”（TN + FP）的样本中，有多少是“预测错了”（FP）的? 这个百分比叫假阳性率（FPR），计算公式：
  $$FalsePositiveRate(FPR)=\frac{FP}{TN+FP}$$

• 假阴性率 ( False Negative Rate，FNR )
  在所有“实际为真”（FN + TP）的样本中，有多少是“预测错了”（FN）的? 这个百分比叫假阴性率（TNR）
  $$FalseNegativeRate(FNR)=\frac{FN}{FN+TP}$$

以上所有概念，只有准确率是以预测数据为参照（作分母）进行度量的，真阳性率、真阴性率、假阳性率、假阴性率都是以实际数据为参照（作分母）进行度量的。以下是它们之间存在的一些关系：

$$召回率(Recall)=真阳性率(TPR)$$
$$真阳性率(TPR)+假阴性率(FNR)=1$$
$$真阴性率(TNR)+假阳性率(FPR)=1$$

参考资料：

机器学习之分类性能度量指标 : ROC曲线、AUC值、正确率、召回率