Leetcode 寻找峰值

为了实现时间复杂度为 O ( log n ) O(\log n) O(logn),可以使用二分查找法:
解题思路:
- 峰值的特性是:当前元素大于左右相邻元素。
- 使用二分法:
- 如果
nums[mid] > nums[mid + 1],说明峰值在左侧或当前mid位置(包括mid),因此将right = mid。 - 否则峰值在右侧,因此将
left = mid + 1。
- 如果
- 不断收缩区间,直到
left == right,此时即找到峰值。
时间复杂度:
- 时间复杂度:(O(\log n)),因为每次迭代都将搜索范围减半。
- 空间复杂度:(O(1)),不需要额外的空间。
java 实现
class Solution {public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;// 如果中点比右侧元素大,说明峰值在左侧(包括mid)if (nums[mid] > nums[mid + 1]) {right = mid;} else { // 否则峰值在右侧left = mid + 1;}}// 最终left和right会相遇,此时即为峰值位置return left;}
}
数组即便不是有序的,为什么仍然二分查找仍然可以找到峰值?
这是因为这道题的二分查找并不依赖于数组是否有序,而是利用了“峰值”的定义和数组的局部特性。
关键点
-
题目定义的峰值条件:
- 峰值是指某个元素严格大于其左右邻居的元素。
- 如果一个元素
nums[mid] > nums[mid + 1],那么在mid或者其左侧一定存在一个峰值。 - 如果
nums[mid] < nums[mid + 1],那么在mid的右侧一定存在一个峰值。
-
为什么可以二分?
二分查找的核心在于:- 每次选择一个中间点
mid,并根据某个条件判断下一个搜索范围。 - 在这道题中,“峰值”可以通过比较
nums[mid]和nums[mid + 1]来判断范围:- 如果
nums[mid] > nums[mid + 1]:- 峰值在左侧或就是
mid,因为mid本身比右边的大(局部性质),可以舍弃右侧部分。
- 峰值在左侧或就是
- 如果
nums[mid] < nums[mid + 1]:- 峰值一定在右侧,因为右边存在一个更大的值,最终会到达一个下降点形成峰值。
- 如果
这利用了“递增到下降”的局部特性来缩小搜索范围。
- 每次选择一个中间点
-
数学直观解释:
- 假设数组中不存在连续相等的数字(即没有平缓区域),并且在数组两端可以假想有值为负无穷的元素(题目已假设
nums[-1] = nums[n] = -∞)。 - 在数组中总能找到一个峰值元素,原因是:
- 如果数组中存在一个“上升”趋势,例如
nums[i] < nums[i+1],那么在右侧一定有一个峰值。 - 如果数组中存在一个“下降”趋势,例如
nums[i] > nums[i+1],那么左侧也一定存在一个峰值。
- 如果数组中存在一个“上升”趋势,例如
这种趋势保证了每次二分缩小范围后,最终一定会收敛到某个峰值点。
- 假设数组中不存在连续相等的数字(即没有平缓区域),并且在数组两端可以假想有值为负无穷的元素(题目已假设
-
非有序数组的适用性:
题目并没有要求数组有序。因为峰值是局部性质(仅与相邻元素有关),只需要每次确定搜索方向,而不是依赖整体有序性。二分查找法的效率仍然得以保证。
举例说明
以数组 nums = [1, 2, 1, 3, 5, 6, 4] 为例:
- 初始:
left = 0, right = 6,取中间点mid = 3,nums[mid] = 3。- 比较
nums[mid]和nums[mid + 1],3 < 5,说明右侧有峰值,更新left = mid + 1。
- 第二轮:
left = 4, right = 6,取中间点mid = 5,nums[mid] = 6。- 比较
nums[mid]和nums[mid + 1],6 > 4,说明左侧有峰值,更新right = mid。
- 第三轮:
left = 4, right = 5,取中间点mid = 4,nums[mid] = 5。- 比较
nums[mid]和nums[mid + 1],5 < 6,说明右侧有峰值,更新left = mid + 1。
- 最终:
left = right = 5,返回5,此时峰值为6。
总结
二分查找法在这道题中能用,是因为:
- 峰值的定义是局部性质,不依赖数组整体有序性。
- 每次比较中点和其右侧元素,可以有效缩小搜索范围。
- 这种方法本质上是利用数组的递增和递减趋势来确定峰值位置。
相关文章:

Leetcode 寻找峰值
为了实现时间复杂度为 O ( log n ) O(\log n) O(logn),可以使用二分查找法: 解题思路: 峰值的特性是:当前元素大于左右相邻元素。使用二分法: 如果 nums[mid] > nums[mid 1],说明峰值在左侧或当前…...
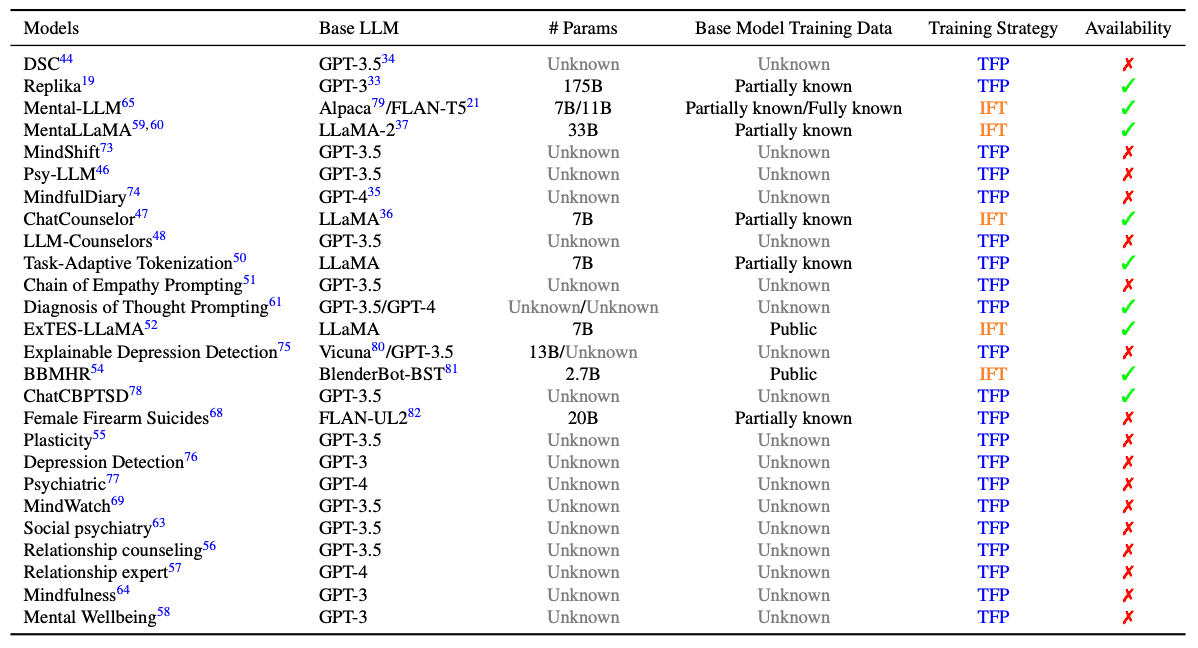
探索大规模语言模型(LLM)在心理健康护理领域中的应用与潜力
概述 心理健康是公共卫生最重要的领域之一。根据美国国家精神卫生研究所(NIMH)的数据,到 2021 年,22.8% 的美国成年人将患上某种形式的精神疾病。在全球范围内,精神疾病占非致命性疾病负担的 30%,并被世界…...

Infisical开源密钥管理平台实战指南
1. 引言 在现代软件开发中,安全地管理环境变量和敏感信息已成为一个关键挑战。Infisical作为一个开源的密钥管理平台,为这一问题提供了强大而灵活的解决方案。本指南将深入探讨Infisical的功能,并通过实际操作步骤,帮助读者全面了解和使用这个工具。 2. Infisical概述 I…...

AI大模型:重塑软件开发流程与模式
人工智能技术的飞速发展,尤其是AI大模型的兴起,正以前所未有的速度和深度影响着各行各业,其中软件开发领域尤为显著。AI大模型,如GPT系列、BERT、Claude等通过其强大的自然语言处理能力、代码理解和生成能力,正在从根本…...

AMD(Xilinx) FPGA配置Flash大小选择
目录 1 FPGA配置Flash大小的决定因素2 为什么选择的Flash容量大小为最小保证能够完成整个FPGA的配置呢? 1 FPGA配置Flash大小的决定因素 在进行FPGA硬件设计时,选择合适的配置Flash是我们进行硬件设计必须考虑的,那么配置Flash大小的选择由什…...
基于Java Springboot图书借阅系统
一、作品包含 源码数据库设计文档万字PPT全套环境和工具资源部署教程 二、项目技术 前端技术:Html、Css、Js、Vue、Element-ui 数据库:MySQL 后端技术:Java、Spring Boot、MyBatis 三、运行环境 开发工具:IDEA/eclipse 数据…...

DDRPHY数字IC后端设计实现系列专题之数字后端floorplanpowerplan设计
3.2.3 特殊单元的布局 布图阶段除了布置 I/O 单元和宏单元,在 28nm 制程工艺时,还需要处理两种特 殊的物理单元,Endcap 和 Tapcell。 DDRPHY数字IC后端设计实现系列专题之后端设计导入,IO Ring设计 (1)拐…...

【Mysql】Mysql函数(上)
1、概述 在Mysql中,为了提高代码重用性和隐藏实现细节,Mysql提供了很多函数。函数可以理解为封装好的模块代码。 2、分类 在Mysql中,函数非常多,主要可以分为以下几类: (1)聚合函数 …...

Java连接MySQL(测试build path功能)
Java连接MySQL(测试build path功能) 实验说明下载MySQL的驱动jar包连接测试的Java代码 实验说明 要测试该情况,需要先安装好MySQL的环境,其实也可以通过测试最后提示的输出来判断build path是否成功,因为如果不成功会直…...

卡尔曼滤波器
卡尔曼滤波器概述 卡尔曼滤波器(Kalman Filter)是一种递归的最优估计方法,广泛应用于信号处理、控制理论、导航定位等领域。它基于线性动态系统模型,通过观测数据不断更新系统的状态估计,从而使得估计值能够在噪声干扰…...

基于BERT的情感分析
基于BERT的情感分析 1. 项目背景 情感分析(Sentiment Analysis)是自然语言处理的重要应用之一,用于判断文本的情感倾向,如正面、负面或中性。随着深度学习的发展,预训练语言模型如BERT在各种自然语言处理任务中取得了…...

推荐15个2024最新精选wordpress模板
以下是推荐的15个2024年最新精选WordPress模板,轻量级且SEO优化良好,适合需要高性能网站的用户。中文wordpress模板适合搭建企业官网使用。英文wordpress模板,适合B2C网站搭建,功能强大且兼容性好,是许多专业外贸网站的…...

AWTK-WIDGET-WEB-VIEW 实现笔记 (2) - Windows
在 Windows 平台上的实现,相对比较顺利,将一个窗口嵌入到另外一个窗口是比较容易的事情。 1. 创建窗口 这里有点需要注意: 父窗口的大小变化时,子窗口也要跟着变化,否则 webview 显示不出来。创建时窗口的大小先设置…...

Linux四剑客及正则表达式
正则表达式 基础正则(使用四剑客命令时无需加任何参数即可使用) ^ # 匹配以某一内容开头 如:^grep匹配所有以grep开头的行。 $ # 匹配以某一内容结尾 如:grep$ 匹配所有以grep结尾的行。 ^$ # 匹配空行。 . # 匹配…...
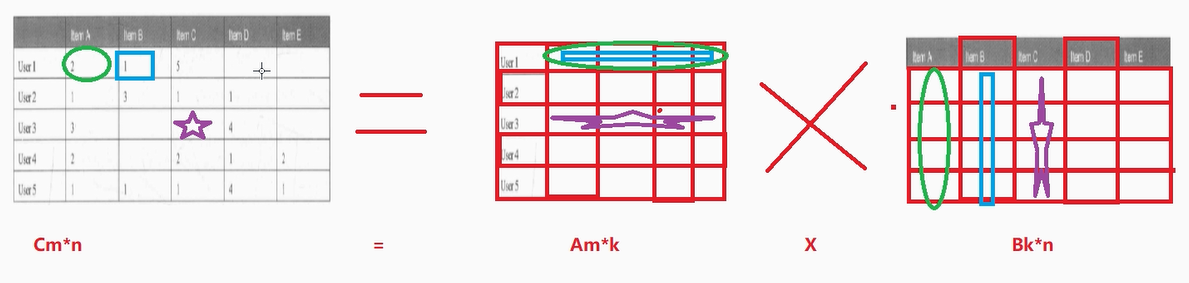
ALS 推荐算法案例演示(python)
数学知识补充:矩阵 总结来说: Am*k X Bk*n Cm*n ----至于乘法的规则,是数学问题, 知道可以乘即可,不需要我们自己计算 反过来 Cm*n Am*k X Bk*n ----至于矩阵如何拆分/如何分解,是数学问题,知道可以拆/可以分解即可 ALS 推荐算法案例:电影推…...

labview中连接sql server数据库查询语句
当使用数据库查询功能时,我们需要用到数据库的查询语句,这里已调用sql server为例,我们需要按照时间来查询,这里在正常调用数据库查询语句时,我们需要在前面给他加一个限制条件这里用到了,数据库的查询语句…...

leetcode_二叉树最大深度
对二叉树的理解 对递归调用的理解 对内存分配的理解 基础数据结构(C版本) - 飞书云文档 每次函数的调用 都会进行一次新的栈内存分配 所以lmax和rmax的值不会混在一起 /*** Definition for a binary tree node.* struct TreeNode {* int val;* …...

Elasticsearch 重建索引 数据迁移
Elasticsearch 重建索引 数据迁移 处理流程创建临时索引数据迁移重建索引写在最后 大家都知道,es的索引创建完成之后就不可以再修改了,包括你想更改字段属性或者是分词方式等。那么随着业务数据量的发展,可能会出现需要修改索引,或…...

2411rust,异步函数
原文 Rust异步工作组很高兴地宣布,在实现在特征中使用异步 fn的目标方面取得了重大进度.将在下周发布稳定的Rust1.75版,会包括特征中支持impl Trait注解和async fn. 稳定化 自从RFC#1522在Rust1.26中稳定下来以来,Rust就允许用户按函数的返回类型(一般叫"RPIT")编…...

前端网络性能优化问题
DNS预解析 DNS 解析也是需要时间的,可以通过预解析的⽅式来预先获得域名所对应的 IP。 <link rel"dns-prefetch" href"//abcd.cn"> 缓存 强缓存 在缓存期间不需要请求, state code 为 200 可以通过两种响应头实现&#…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
