力扣周赛:第424场周赛
👨🎓作者简介:爱好技术和算法的研究生
🌌上期文章:力扣周赛:第422场周赛
📚订阅专栏:力扣周赛
希望文章对你们有所帮助
第一道题模拟题,第二道题经典拆分数组/线段树都可以做,这两个要是都不会那就是基础不行,需要差缺补漏了。第三题那个味太足了,一看那个答案的顺序性就知道要二分答案了,也很简单。
力扣周赛:第424场周赛
- 使数组元素等于零
- 零数组变换 I
- 零数组变换 II
使数组元素等于零
题目描述
给你一个整数数组 nums 。
开始时,选择一个满足 nums[curr] == 0 的起始位置 curr ,并选择一个移动 方向 :向左或者向右。
此后,你需要重复下面的过程:
- 如果 curr 超过范围 [0, n - 1] ,过程结束。
- 如果 nums[curr] == 0 ,沿当前方向继续移动:如果向右移,则 递增 curr ;如果向左移,则 递减 curr 。
- 如果 nums[curr] > 0:
-
- 将 nums[curr] 减 1 。
-
- 反转 移动方向(向左变向右,反之亦然)。
-
- 沿新方向移动一步。
如果在结束整个过程后,nums 中的所有元素都变为 0 ,则认为选出的初始位置和移动方向 有效 。
返回可能的有效选择方案数目。
示例1

示例2
输入:nums = [2,3,4,0,4,1,0]
输出:0
解释:
不存在有效的选择方案。
提示
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 100
- 至少存在一个元素 i 满足 nums[i] == 0 。
模拟题,没啥好说的
class Solution {public int countValidSelections(int[] nums) {int ans = 0;for(int i = 0; i < nums.length; ++i){if(nums[i] == 0){int[] temp1 = new int[nums.length];int[] temp2 = new int[nums.length];for(int j = 0; j < nums.length; ++j){temp1[j] = nums[j];temp2[j] = nums[j];}if(check(temp1, i, 1))ans++;if(check(temp2, i, -1))ans++;}}return ans;}public boolean check(int[] nums, int cur, int dir){while(true){cur = cur + dir;if(cur < 0 || cur == nums.length)break;if(nums[cur] > 0){nums[cur]--;dir *= -1;}}for(int i = 0; i < nums.length; ++i){if(nums[i] != 0)return false;}return true;}
}
零数组变换 I
题目描述
给定一个长度为 n 的整数数组 nums 和一个二维数组 queries,其中 queries[i] = [li, ri]。
对于每个查询 queries[i]:
- 在 nums 的下标范围 [li, ri] 内选择一个下标子集。
- 将选中的每个下标对应的元素值减 1。
零数组 是指所有元素都等于 0 的数组。
如果在按顺序处理所有查询后,可以将 nums 转换为 零数组 ,则返回 true,否则返回 false。
数组的 子集 是对数组元素的选择(可能为空)。
示例1
输入: nums = [1,0,1], queries = [[0,2]]
输出: true
解释:
- 对于 i = 0:
选择下标子集 [0, 2] 并将这些下标处的值减 1。
数组将变为 [0, 0, 0],这是一个零数组。
示例2
输入: nums = [4,3,2,1], queries = [[1,3],[0,2]]
输出: false
解释:
- 对于 i = 0:
选择下标子集 [1, 2, 3] 并将这些下标处的值减 1。
数组将变为 [4, 2, 1, 0]。 - 对于 i = 1:
选择下标子集 [0, 1, 2] 并将这些下标处的值减 1。
数组将变为 [3, 1, 0, 0],这不是一个零数组。
提示
- 1 <= nums.length <= 105
- 0 <= nums[i] <= 105
- 1 <= queries.length <= 105
- queries[i].length == 2
- 0 <= li <= ri < nums.length
很显然是拆分数组,直接维护一个f,其中f[i]表示nums[i]共处在哪些区间中,只要f[i] >= nums[i],则说明肯定是可以在queries中将其处理到0。
所以问题转化为某个下标处在哪些区间中,对于每个query的起始点start和终止点end,只需要让f[start]++和f[end + 1]–,即可维护这部分关系了。
class Solution {public boolean isZeroArray(int[] nums, int[][] queries) {int[] f = new int[nums.length];for(int[] query : queries){int start = query[0], end = query[1];f[start]++;if(end + 1 >= nums.length)continue;f[end + 1]--;}int sum=0;for(int i = 0; i < nums.length; ++i){sum += f[i];if(nums[i] > sum)return false;}return true;}
}
零数组变换 II
题目描述
给你一个长度为 n 的整数数组 nums 和一个二维数组 queries,其中 queries[i] = [li, ri, vali]。
每个 queries[i] 表示在 nums 上执行以下操作:
- 将 nums 中 [li, ri] 范围内的每个下标对应元素的值 最多 减少 vali。
- 每个下标的减少的数值可以独立选择。
零数组 是指所有元素都等于 0 的数组。
返回 k 可以取到的 最小非负 值,使得在 顺序 处理前 k 个查询后,nums 变成 零数组。如果不存在这样的 k,则返回 -1。
示例1
输入: nums = [2,0,2], queries = [[0,2,1],[0,2,1],[1,1,3]]
输出: 2
解释:
- 对于 i = 0(l = 0, r = 2, val = 1):
-
- 在下标 [0, 1, 2] 处分别减少 [1, 0, 1]。
-
- 数组将变为 [1, 0, 1]。
- 对于 i = 1(l = 0, r = 2, val = 1):
-
- 在下标 [0, 1, 2] 处分别减少 [1, 0, 1]。
-
- 数组将变为 [0, 0, 0],这是一个零数组。因此,k 的最小值为 2。
示例2
输入: nums = [4,3,2,1], queries = [[1,3,2],[0,2,1]]
输出: -1
解释:
- 对于 i = 0(l = 1, r = 3, val = 2):
-
- 在下标 [1, 2, 3] 处分别减少 [2, 2, 1]。
-
- 数组将变为 [4, 1, 0, 0]。
- 对于 i = 1(l = 0, r = 2, val = 1):
-
- 在下标 [0, 1, 2] 处分别减少 [1, 1, 0]。
-
- 数组将变为 [3, 0, 0, 0],这不是一个零数组。
提示
- 1 <= nums.length <= 105
- 0 <= nums[i] <= 5 * 105
- 1 <= queries.length <= 105
- queries[i].length == 3
- 0 <= li <= ri < nums.length
- 1 <= vali <= 5
这个顺序性味太足了,直接二分答案是不会超时的,当然了你还是还想优化也可以,因为那个拆分数组肯定是可以在每次复用的时候被二分的。
记得特判一下,我没特判wa了一发。
class Solution {public int minZeroArray(int[] nums, int[][] queries) {int n = nums.length;int now = 0;for(int i = 0; i < n; ++i)now += nums[i];if(now == 0)return 0;int l = 0, r = queries.length - 1;while(l <= r){int mid = (l + r) >> 1;int[] f = new int[n];for(int i = 0; i <= mid; ++i){int start = queries[i][0], end = queries[i][1], val = queries[i][2];f[start] += val;if(end + 1 >= n)continue;f[end + 1] -= val;}int sum = 0;boolean flag = true;for(int i = 0; i < n; ++i){sum += f[i];if(nums[i] > sum){flag = false;break;}}if(!flag){l = mid + 1;}else{r = mid - 1;}}return l >= queries.length ? -1 : l + 1;}
}
相关文章:

力扣周赛:第424场周赛
👨🎓作者简介:爱好技术和算法的研究生 🌌上期文章:力扣周赛:第422场周赛 📚订阅专栏:力扣周赛 希望文章对你们有所帮助 第一道题模拟题,第二道题经典拆分数组/线段树都…...

预处理(1)(手绘)
大家好,今天给大家分享一下编译器预处理阶段,那么我们来看看。 上面是一些预处理阶段的知识,那么明天给大家讲讲宏吧。 今天分享就到这里,谢谢大家!!...

利用OpenAI进行测试需求分析——从电商网站需求到测试用例的生成
在软件测试工程师的日常工作中,需求分析是测试工作中的关键步骤。需求文档决定了测试覆盖的范围和测试策略,而测试用例的编写往往依赖于需求的准确理解。传统手工分析需求耗时长,尤其在面对大量需求和复杂逻辑时容易遗漏细节。本文将以电商网…...

深入探索:Scrapy深度爬取策略与实践
标题:深入探索:Scrapy深度爬取策略与实践 引言 在数据驱动的时代,深度爬取成为了获取丰富信息的重要手段。Scrapy,作为一个强大的Python爬虫框架,提供了多种工具和设置来帮助我们实现深度爬取。本文将详细介绍如何在…...

《生成式 AI》课程 第3講:訓練不了人工智慧嗎?你可以訓練你自己
资料来自李宏毅老师《生成式 AI》课程,如有侵权请通知下线 Introduction to Generative AI 2024 Spring 摘要 这一系列的作业是为 2024 年春季的《生成式 AI》课程设计的,共包含十个作业。每个作业都对应一个具体的主题,例如真假难辨的世界…...

如何编译 Cesium 源码
如何编译 Cesium 源码 Cesium 是一个开源的 JavaScript 库,用于构建 3D 地球和地图应用程序。它提供了一套强大的 API 和工具,使开发者能够创建丰富的地理空间应用。本文将指导您如何从 GitHub 下载 Cesium 源码,并在本地进行编译。 TilesB…...

前端开发设计模式——责任链模式
目录 一、定义和特点 1. 定义 2. 特点 二、实现方式 定义抽象处理者(Handler)类 创建具体处理者(ConcreteHandler)类 构建责任链 以下是一个用 JavaScript 实现的示例: 三、应用场景 1. 表单验证 2. 请求处…...

JavaWeb--MySQL
1. MySQL概述 首先来了解一下什么是数据库。 数据库:英文为 DataBase,简称DB,它是存储和管理数据的仓库。 像我们日常访问的电商网站京东,企业内部的管理系统OA、ERP、CRM这类的系统,以及大家每天都会刷的头条、抖音…...

Python | Leetcode Python题解之第564题数组嵌套
题目: 题解: class Solution:def arrayNesting(self, nums: List[int]) -> int:ans, n 0, len(nums)for i in range(n):cnt 0while nums[i] < n:num nums[i]nums[i] ni numcnt 1ans max(ans, cnt)return ans...
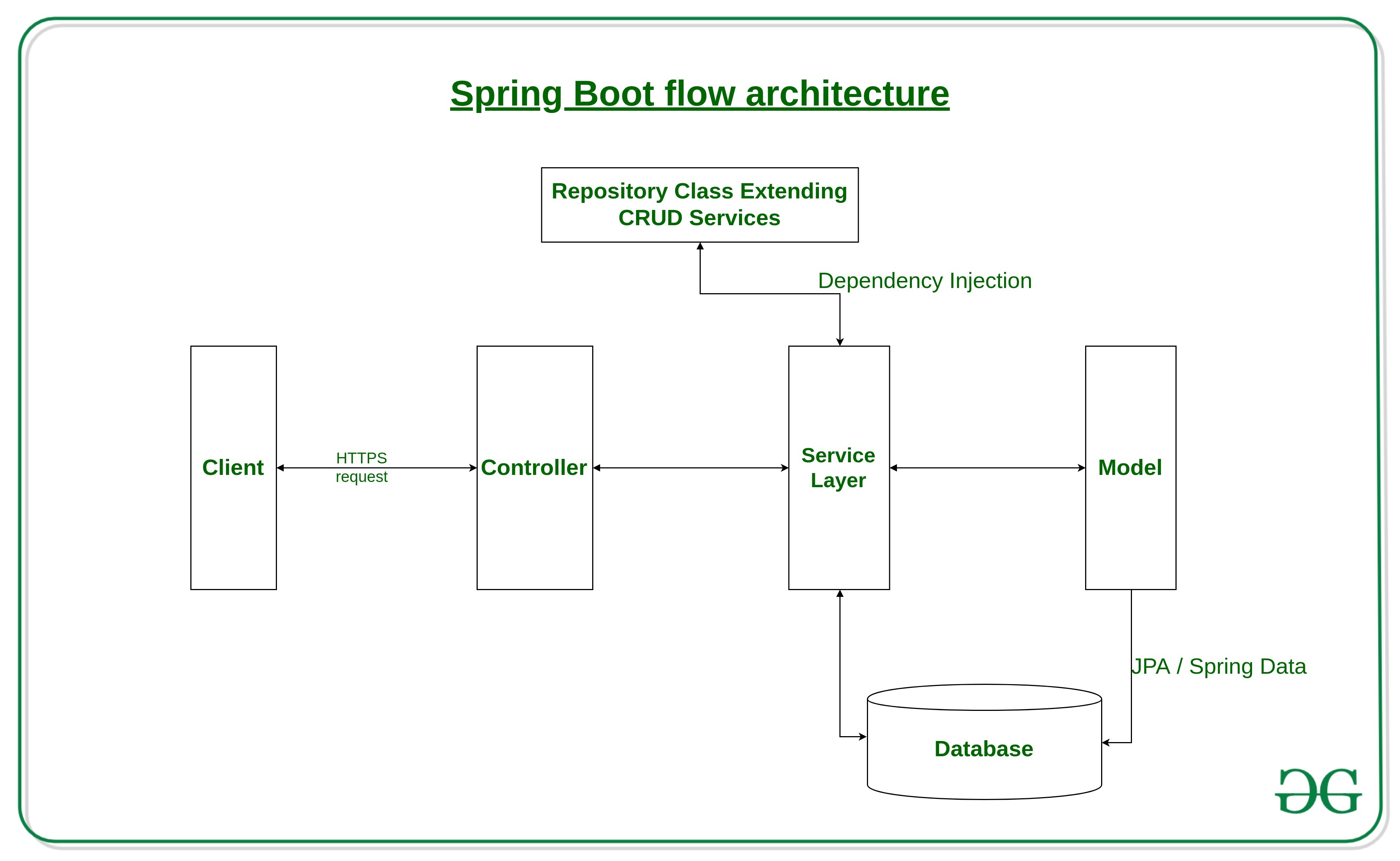
Spring Boot教程之Spring Boot简介
Spring Boot 简介 接下来一段时间,我会持续发布并完成Spring Boot教程 Spring 被广泛用于创建可扩展的应用程序。对于 Web 应用程序,Spring 提供了 Spring MVC,它是 Spring 的一个广泛使用的模块,用于创建可扩展的 Web 应用程序。…...

Qwen2-VL:发票数据提取、视频聊天和使用 PDF 的多模态 RAG 的实践指南
概述 随着人工智能技术的迅猛发展,多模态模型在各类应用场景中展现出强大的潜力和广泛的适用性。Qwen2-VL 作为最新一代的多模态大模型,融合了视觉与语言处理能力,旨在提升复杂任务的执行效率和准确性。本指南聚焦于 Qwen2-VL 在三个关键领域…...

【安全科普】NUMA防火墙诞生记
一、我为啥姓“NUMA” 随着网络流量和数据包处理需求的指数增长,曾经的我面对“高性能、高吞吐、低延迟”的要求,逐渐变得心有余而力不足。 多CPU技术应运而生,SMP(对称多处理)和NUMA(非一致性内存访问&a…...

机器学习day2-特征工程
四.特征工程 1.概念 一般使用pandas来进行数据清洗和数据处理、使用sklearn来进行特征工程 将任意数据(文本或图像等)转换为数字特征,对特征进行相关的处理 步骤:1.特征提取;2.无量纲化(预处理…...

Python数据分析NumPy和pandas(三十五、时间序列数据基础)
时间序列数据是许多不同领域的结构化数据的重要形式,例如金融、经济、生态学、神经科学和物理学。在许多时间点重复记录的任何内容都会形成一个时间序列。许多时间序列是固定频率的,也就是说,数据点根据某些规则定期出现,例如每 1…...
常见错误及排查)
Python 小高考篇(6)常见错误及排查
目录 TypeError拼接字符串和数字错误示范正确示范 数字、字符串当成函数错误示范 给函数传入未被定义过的参数错误示范 传入的参数个数不正确错误示范 字符串相乘错误示范正确示范 量取整数的长度错误示范正确示范 格式化字符串时占位符个数不正确错误示范 给复数比较大小错误示…...

k8s上部署redis高可用集群
介绍: Redis Cluster通过分片(sharding)来实现数据的分布式存储,每个master节点都负责一部分数据槽(slot)。 当一个master节点出现故障时,Redis Cluster能够自动将故障节点的数据槽转移到其他健…...

C++的类和对象
在C中,类(class)和对象(object)是面向对象编程(OOP)的核心概念。以下是它们的详细介绍: 1. 类(Class) 定义: 类是用来定义一个新的数据类型&…...

自动驾驶系列—深入解析自动驾驶车联网技术及其应用场景
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...

机器学习(1)
一、机器学习 机器学习(Machine Learning, ML)是人工智能(Artificial Intelligence, AI)的一个分支,它致力于开发能够从数据中学习并改进性能的算法和模型。机器学习的核心思想是通过数据和经验自动优化算法ÿ…...

深入理解 Redis跳跃表 Skip List 原理|图解查询、插入
1. 简介 跳跃表 ( skip list ) 是一种有序数据结构,通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。 在 Redis 中,跳跃表是有序集合键的底层实现之一,那么这篇文章我们就来讲讲跳跃表的实现原理。 2. …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
