代码随想录算法训练营第六十天|KM94.城市间货物运输Ⅰ|KM95.城市间货物运输Ⅱ|KM96.城市间货物运输Ⅲ
94. 城市间货物运输 I
2、Bellman_ford队列优化算法(又名SPFA)
SPFA是对Bellman_ford算法的优化,由于Bellman_ford 算法 每次都是对所有边进行松弛,其实是多做了一些无用功。其实只需要对 上一次松弛的时候更新过的节点作为出发节点所连接的边 进行松弛就够了。
import collectionsdef main():n, m = map(int, input().strip().split())edges = [[] for _ in range(n+1)]for _ in range(m):src, dest, weight = map(int, input().strip().split())edges[src].append([dest, weight])# 初始化minDist = [float('inf')] * (n+1)# 第一个节点为0minDist[1] = 0que = collections.deque([1])visited = [False] * (n+1)visited[1] = Truewhile que:cur = que.popleft()visited[cur] = Falsefor dest, weight in edges[cur]:if minDist[cur] != float('inf') and minDist[cur] + weight < minDist[dest]:minDist[dest] = minDist[cur] + weightif visited[dest] == False:que.append(dest)visited[dest] = Trueif minDist[-1] == float('inf'):print('unconnnected')return minDist[-1]if __name__ == '__main__':print(main())95. 城市间货物运输 II
本题是要我们判断 负权回路,也就是图中出现环且环上的边总权值为负数。
如果在这样的图中求最短路的话, 就会在这个环里无限循环 (也是负数+负数 只会越来越小),无法求出最短路径。(有负权回路的情况下,一直都会有更短的最短路,所以 松弛 第n次,minDist数组 也会发生改变。)
import collections
from math import inf
def main():n, m = map(int, input().strip().split())edges = [[] for _ in range(n+1)]# 记录节点接入队列的次数count = [0 for _ in range(n+1)]for _ in range(m):src, dest, weight = map(int, input().strip().split())edges[src].append([dest, weight])# 初始化minDist = [float('inf')] * (n+1)# 第一个节点为0minDist[1] = 0que = collections.deque([1])count[1] = 1flag = False# 主循环while que:cur = que.popleft()for dest, weight in edges[cur]:if minDist[cur] + weight < minDist[dest]:minDist[dest] = minDist[cur] + weightcount[dest] += 1if dest not in que:que.append(dest)if count[dest] == n:flag = Trueif flag:breakif flag:print('circle')else:if minDist[-1] == float('inf'):print('unconnected')else:print(minDist[-1])if __name__ == '__main__':main()96. 城市间货物运输 III
本题理解起来有点难度,放着等二刷;
使用SPFA方法求解单源有限最短路;
from collections import deque
from math import infdef main():n, m = [int(i) for i in input().split()]graph = [[] for _ in range(n+1)]for _ in range(m):v1, v2, val = [int(i) for i in input().split()]graph[v1].append([v2, val])src, dst, k = [int(i) for i in input().split()]min_dist = [inf for _ in range(n+1)]min_dist[src] = 0 # 初始化起点的距离que = deque([src])while k != -1 and que:visited = [False for _ in range(n+1)] # 用于保证每次松弛时一个节点最多加入队列一次que_size = len(que)temp_dist = min_dist.copy() # 用于记录上一次遍历的结果for _ in range(que_size):cur_node = que.popleft()for next_node, val in graph[cur_node]:if min_dist[next_node] > temp_dist[cur_node] + val:min_dist[next_node] = temp_dist[cur_node] + valif not visited[next_node]:que.append(next_node)visited[next_node] = Truek -= 1if min_dist[dst] == inf:print("unreachable")else:print(min_dist[dst])if __name__ == "__main__":main()
相关文章:

代码随想录算法训练营第六十天|KM94.城市间货物运输Ⅰ|KM95.城市间货物运输Ⅱ|KM96.城市间货物运输Ⅲ
94. 城市间货物运输 I 2、Bellman_ford队列优化算法(又名SPFA) SPFA是对Bellman_ford算法的优化,由于Bellman_ford 算法 每次都是对所有边进行松弛,其实是多做了一些无用功。其实只需要对 上一次松弛的时候更新过的节点作为出发节…...

人工智能学习路线全链路解析
一、基础准备阶段(预计 2-3 个月) (一)数学知识巩固与深化 线性代数(约 1 个月): 矩阵基础:回顾矩阵的定义、表示方法、矩阵的基本运算(加法、减法、乘法)&…...

C++语言的学习路线
C语言的学习路线 C是一种强大的高级编程语言,广泛应用于系统软件、游戏开发、嵌入式系统和高性能应用等多个领域。由于其丰富的功能和灵活性,C是一门值得深入学习的语言。本文旨在为初学者制定一条系统的学习路线,帮助他们循序渐进地掌握C语…...
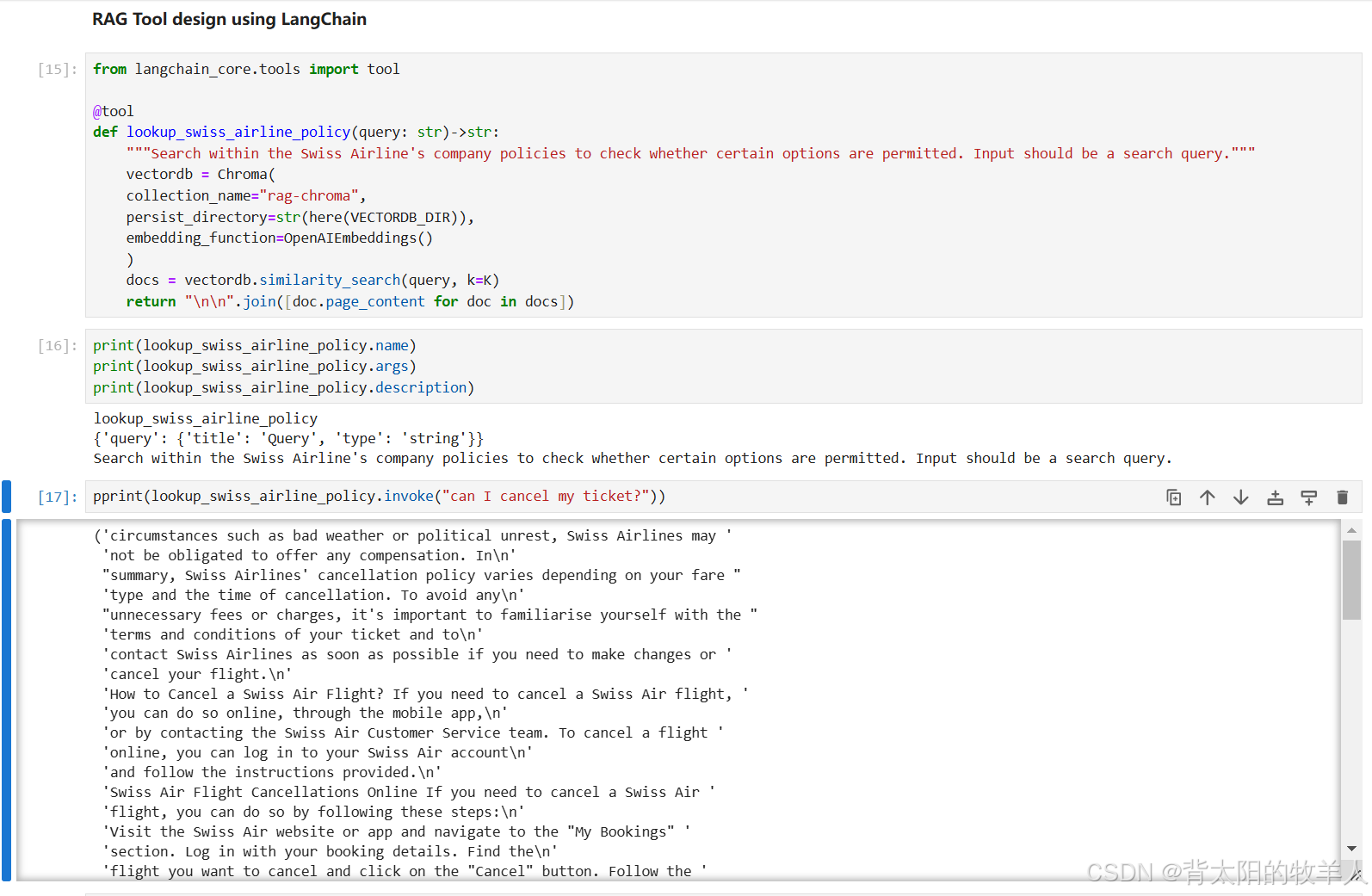
用于与多个数据库聊天的智能 SQL 代理问答和 RAG 系统(3) —— 基于 LangChain 框架的文档检索与问答功能以及RAG Tool的使用
介绍基于 LangChain 框架的文档检索与问答功能,目标是通过查询存储的向量数据库(VectorDB),为用户的问题检索相关内容,并生成自然语言的答案。以下是代码逻辑的详细解析: 代码结构与功能 初始化环境与加载…...
20250110doker学习记录
1.本机创建tts环境。用conda. 0.1安装。我都用的默认,你也可以。我安装过一次,如果修复,后面加 -u bash Anaconda3-2024.10-1-Linux-x86_64.sh等待一会。 (base) ktkt4028:~/Downloads$ conda -V conda 24.9.2学习资源 Conda 常用命令大…...

MPU6050: 卡尔曼滤波, 低通滤波
对于MPU6050(一种集成了三轴加速度计和三轴陀螺仪的惯性测量单元),对加速度值进行卡尔曼滤波,而对角速度进行低通滤波的选择是基于这两种传感器数据的不同特性和应用需求。以下是详细解释: 加速度值与卡尔曼滤波 为什么使用卡尔曼滤波? 噪声抑制: 加速度计信号通常包含…...

C++的标准和C++的编译版本
C的标准和C的编译版本:原理和概念 理解 C标准 和 C编译版本 的关系是学习 C 的一个重要部分。这两者虽然看似相关,但实际上分别涉及了不同的概念和技术。下面将通过层次清晰的解释,帮助新手理解这两个概念的差异、特点及其相互关系。 一、C标…...
python学习笔记—17—数据容器之字符串
1. 字符串 (1) 字符串能通过下标索引来获取其中的元素 (2) 旧字符串无法修改特定下标的元素 (3) index——查找字符串中任意元素在整个字符串中的起始位置(单个字符或字符串都可以) tmp_str "supercarrydoinb" tmp_position1 tmp_str.index("s") tmp_p…...
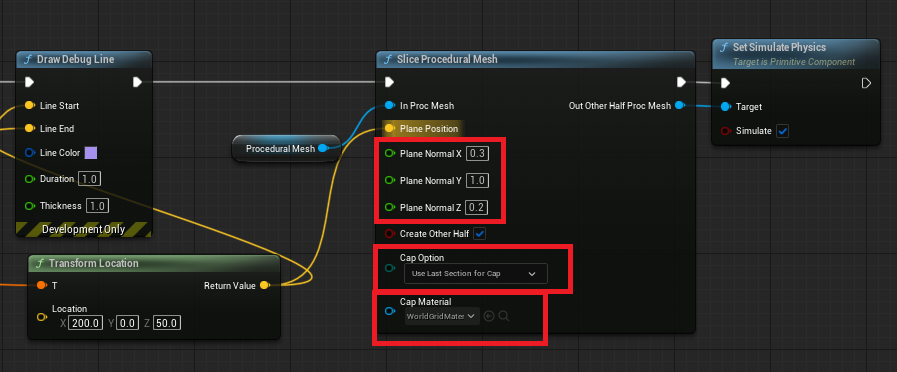
UE5 使用内置组件进行网格切割
UE引擎非常强大,直接内置了网格切割功能并封装为蓝图节点,这项功能在UE4中就存在,并且无需使用Chaos等模块。那么就来学习下如何使用内置组件实现网格切割。 1.配置测试用StaticMesh 对于被切割的模型,需要配置一些参数。以UE5…...
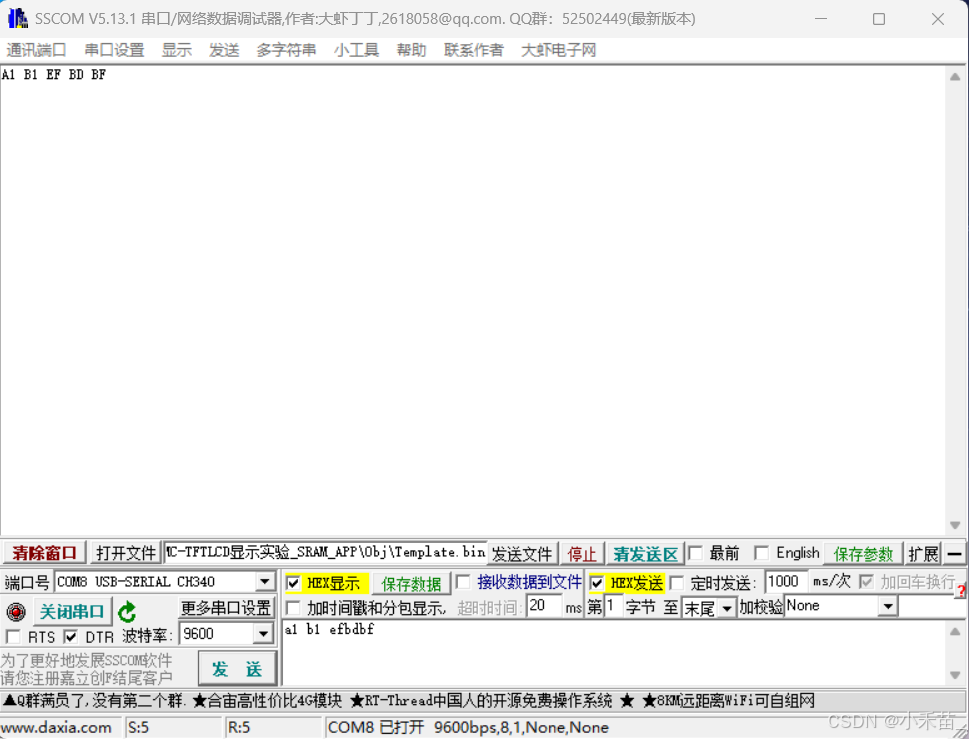
51单片机——串口通信(重点)
1、通信 通信的方式可以分为多种,按照数据传送方式可分为串行通信和并行通信; 按照通信的数据同步方式,可分为异步通信和同步通信; 按照数据的传输方向又可分为单工、半双工和全双工通信 1.1 通信速率 衡量通信性能的一个非常…...

Taro+Vue实现图片裁剪组件
cropper-image-taro-vue3 组件库 介绍 cropper-image-taro-vue3 是一个基于 Vue 3 和 Taro 开发的裁剪工具组件,支持图片裁剪、裁剪框拖动、缩放和输出裁剪后的图片。该组件适用于 Vue 3 和 Taro 环境,可以在网页、小程序等平台中使用。 源码 https:…...
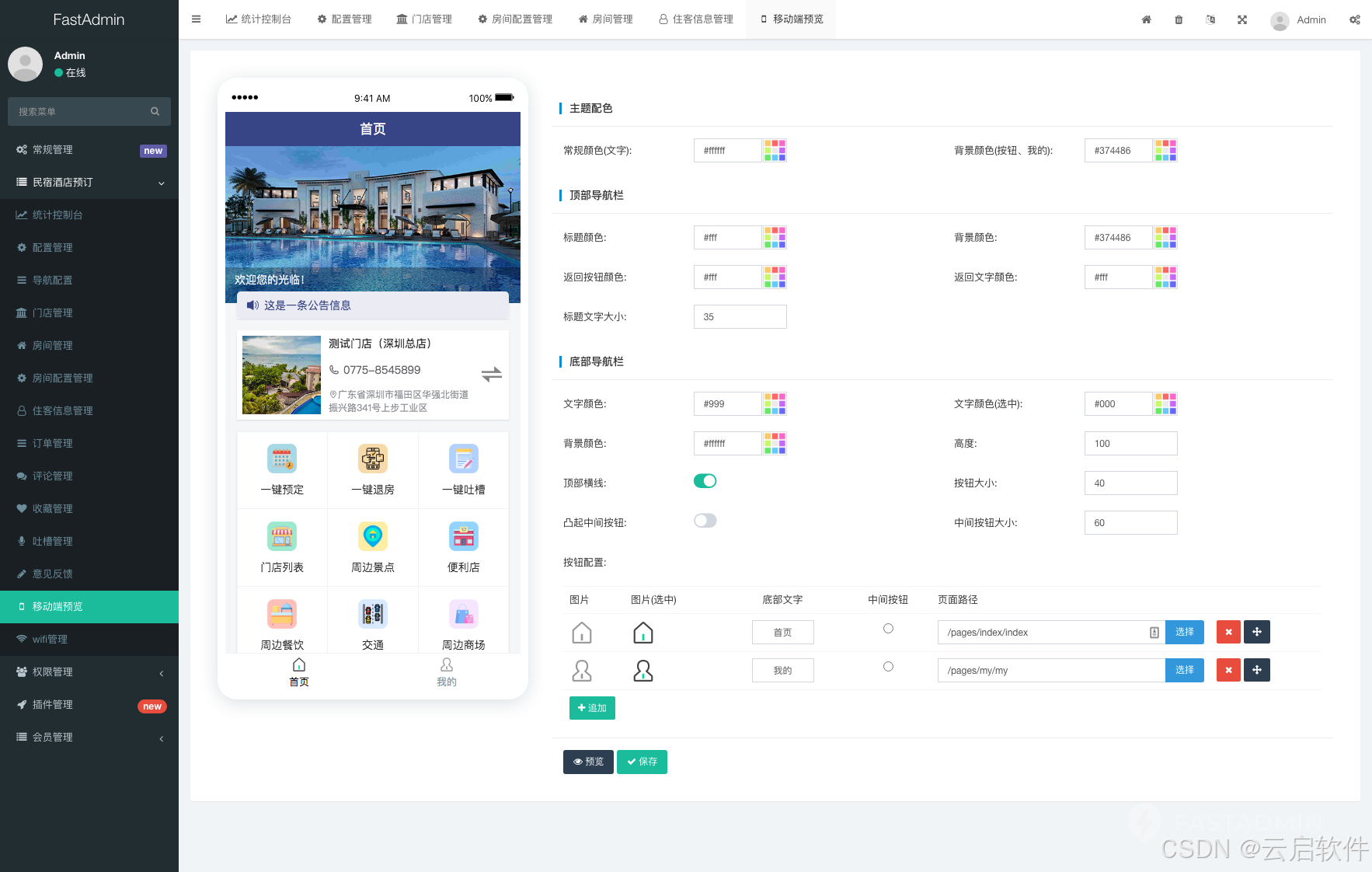
PHP民宿酒店预订系统小程序源码
🏡民宿酒店预订系统 基于ThinkPHPuniappuView框架精心构建的多门店民宿酒店预订管理系统,能够迅速为您搭建起专属的、功能全面且操作便捷的民宿酒店预订小程序。 该系统不仅涵盖了预订、退房、WIFI连接、用户反馈、周边信息展示等核心功能,更…...
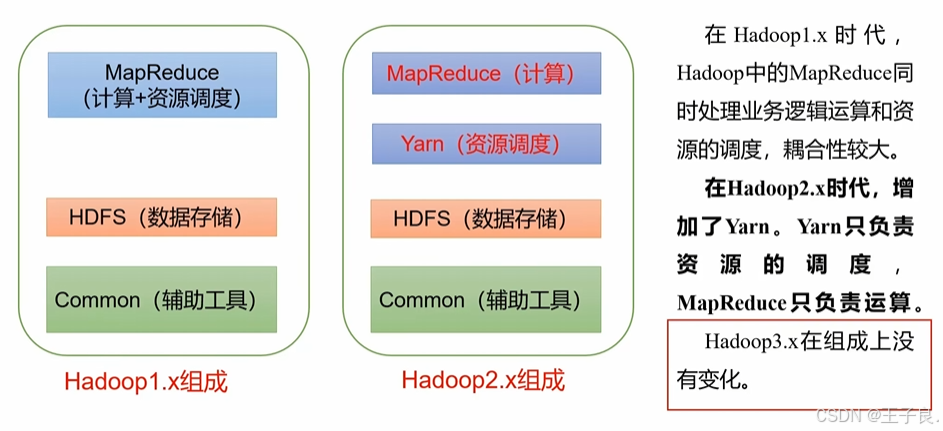
Hadoop3.x 万字解析,从入门到剖析源码
💖 欢迎来到我的博客! 非常高兴能在这里与您相遇。在这里,您不仅能获得有趣的技术分享,还能感受到轻松愉快的氛围。无论您是编程新手,还是资深开发者,都能在这里找到属于您的知识宝藏,学习和成长…...

VUE3 常用的组件介绍
Vue 组件简介 Vue 组件是构建 Vue 应用程序的核心部分,组件帮助我们将 UI 分解为独立的、可复用的块,每个组件都有自己的状态和行为。Vue 组件通常由模板、脚本和样式组成。组件的脚本部分包含了各种配置选项,用于定义组件的逻辑和功能。 组…...

deepin-Wine 运行器合并打包器和添加从镜像提取 DLL 的功能
Wine 运行器是一个图形化工具,旨在简化 Wine 环境的管理和使用。它不仅提供了运行和管理 Wine 容器的功能,还增加了打包器和从镜像提取 DLL 的功能。以下是该工具的详细介绍和使用方法。 一、工具概述 Wine 运行器是一个使用 Python3 的 tkinter 构建的图…...

[大模型]本地离线运行openwebui+ollama容器化部署
本地离线运行Openweb-ui ollama容器化部署 说明安装internet操作内网操作问题线程启动错误最终命令总结说明 最近公司有一个在内网部署一个离线大模型的需求,网络是离线状态,服务器有A100GPU,一开始是想折腾开源chatGML4大模型,因为使用过gml3,所以想着部署gml4应该不难。…...
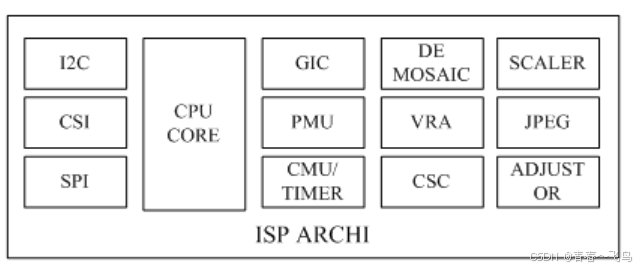
再次梳理ISP的大致流程
前言: 随着智能手机的普及,相机与我们的生活越来越紧密相关。在日常生活中,我们只需要轻轻按下手机上的拍照按钮,就能记录下美好时刻。那么问题来了:从我们指尖按下拍照按钮到一张色彩丰富的照片呈现在我们面前&#x…...
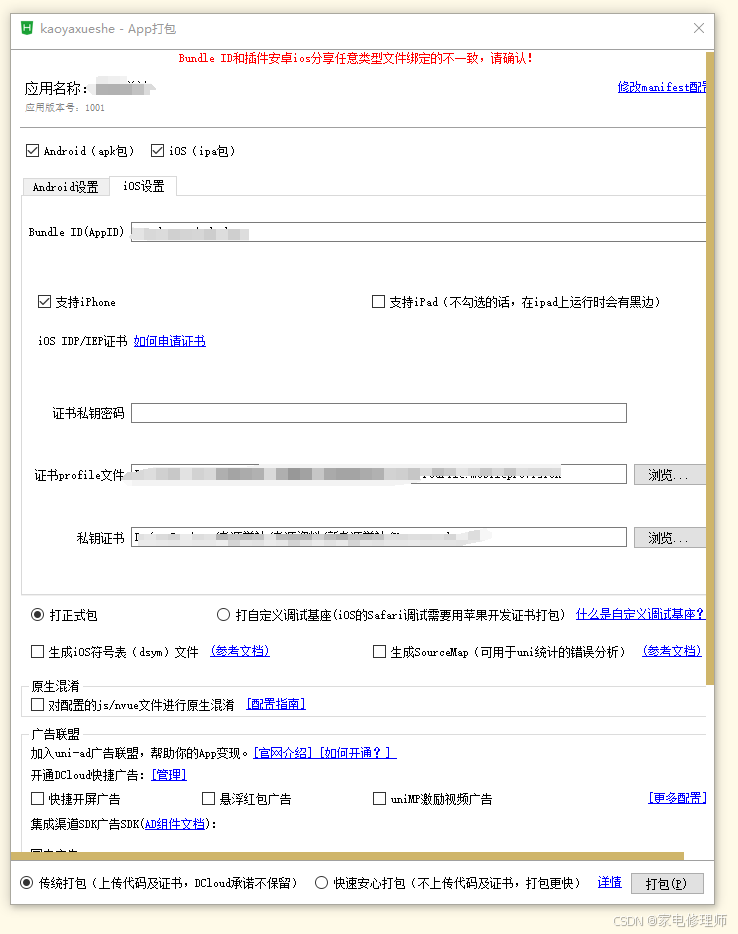
HBuilderX打包ios保姆式教程
1、登录苹果开发者后台并登录已认证开发者账号ID Sign In - Apple 2、创建标识符(App ID)、证书,描述文件 3、首先创建标识符,用于新建App应用 3-1、App的话直接选择第一个App IDs,点击右上角继续 3-2、选择App&#x…...

《解锁鸿蒙系统AI能力,开启智能应用开发新时代》
在当今科技飞速发展的时代,鸿蒙系统以其独特的分布式架构和强大的AI能力,为开发者们带来了前所未有的机遇。本文将深入探讨开发者如何利用鸿蒙系统的AI能力开发更智能的应用,开启智能应用开发的新时代。 鸿蒙系统构筑了15系统级的AI能力&…...

rhcsa练习(3)
1 、创建文件命令练习: ( 1 ) 在 / 目录下创建一个临时目录 test ; mkdir /test ( 2 )在临时目录 test 下创建五个文件,文件名分别为 passwd , group , bashrc &#x…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
