「1」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
第一章 行列式
 的某一行(列)的元素都是两数之和,例如第i行的元素都是两数之和:
的某一行(列)的元素都是两数之和,例如第i行的元素都是两数之和:

矩阵



🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:

「1」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 第一章 行列式 行列式是一个数,是一个结果三阶行列式的计算:主对角线的乘…...

C++7:STL-模拟实现vector
目录 vector的成员变量 构造函数 reserve size() capacity() push_back 一些小BUG 赋值操作符重载 析构函数 【】操作符重载 resize pop_back Insert 迭代器失效 erase 二维数组问题 总结一下 vector,翻译软件会告诉你它的意思是向量,但其…...

笑死,面试官又问我SpringBoot自动配置原理
面试官:好久没见,甚是想念。今天来聊聊SpringBoot的自动配置吧? 候选者:嗯,SpringBoot的自动配置我觉得是SpringBoot很重要的“特性”了。众所周知,SpringBoot有着“约定大于配置”的理念,这一…...
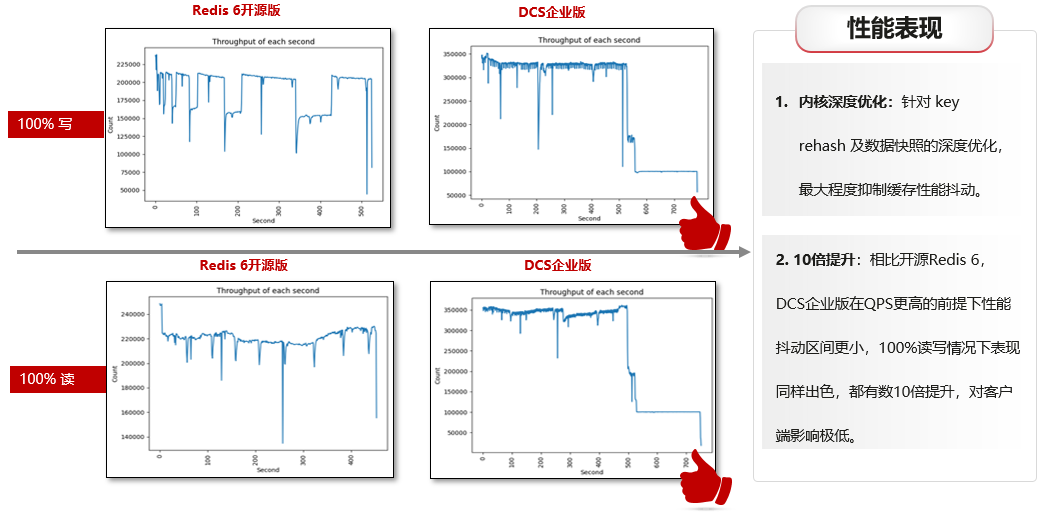
分布式缓存服务DCS-企业版性能更强,稳定性更高
背景介绍 近年来,随着各行业业务需求急速增加,数据量和并发访问量呈指数级增长,原来只能依附于关系型数据库的传统“缓存”逐渐难以支撑上层业务,开源Redis也面临着如“容量有限”、 “可靠性有限”、 “数据重复拷贝,…...

HTTP基本原理
目录URL简单定义格式HTTP和HTTPSHTTP的请求过程。请求响应响应体HTTP2.0总结URL 简单定义 通过一个链接,使我们可以找到网络上的某个资源,这个链接就是URL。 格式 URL并不是随便写的,而是有固定的格式。基本的组成格式如下。 schme://[us…...
最新版本详细保姆级安装教程)
【云原生】Kubernetes(k8s)最新版本详细保姆级安装教程
前言 Kubernetes简称k8s,是一个开源的,用于管理云平台中多个主机上的容器化的应用,k8s目标是让部署容器化的应用简单并且高效,k8s提供了应用部署,规划,更新,维护的一种机制。 本文是总结了在安…...
JVM - 类加载,连接和初始化
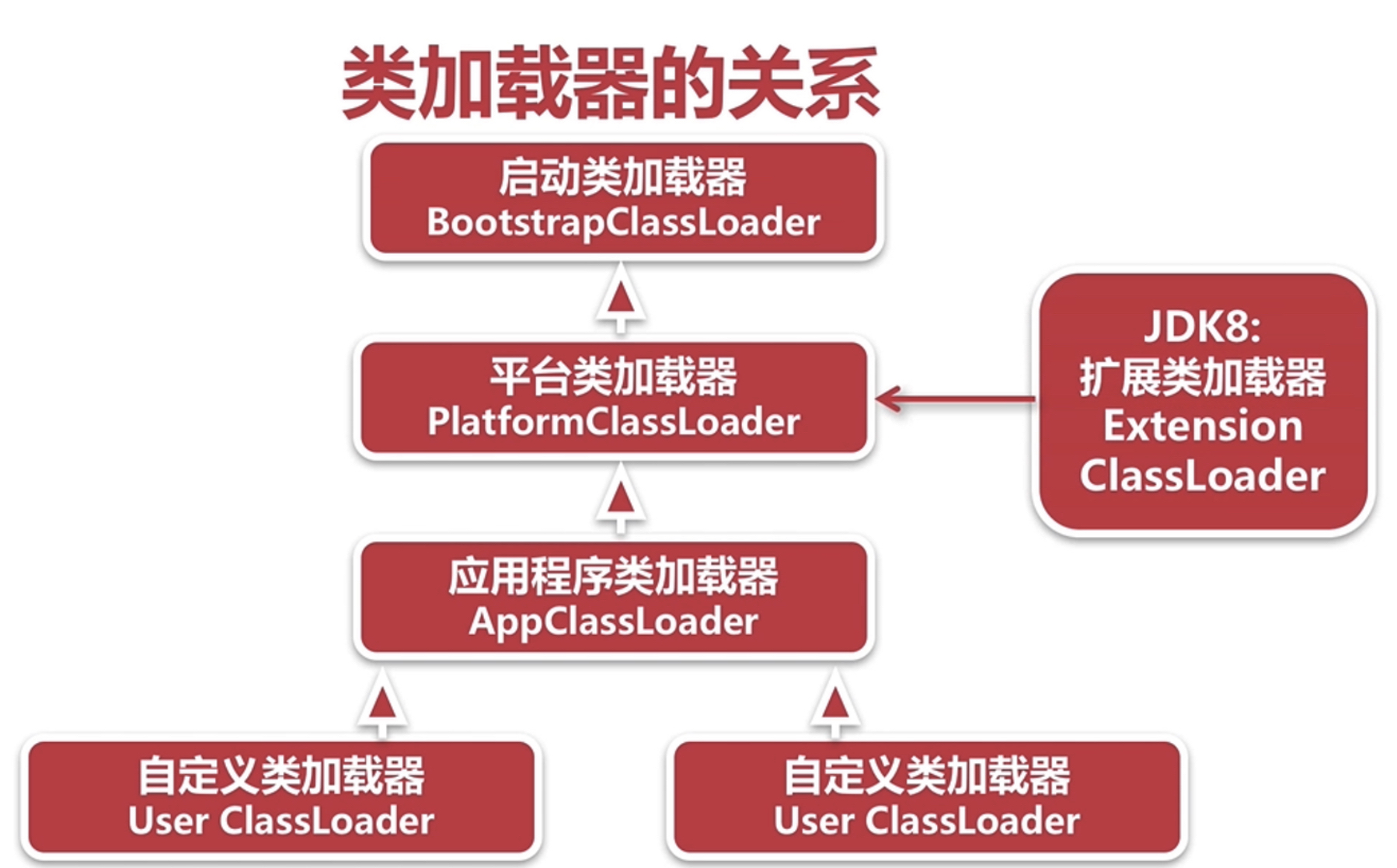
目录 类加载和类加载器 概述 类加载要完成的功能 加载类的方式 类加载器 类加载器的关系 类加载器说明 双亲委派模型 工作过程如下: 双亲委派模型说明: 破坏双亲委派模型: 类连接和初始化 类连接主要验证的内容 类连接中的解析…...
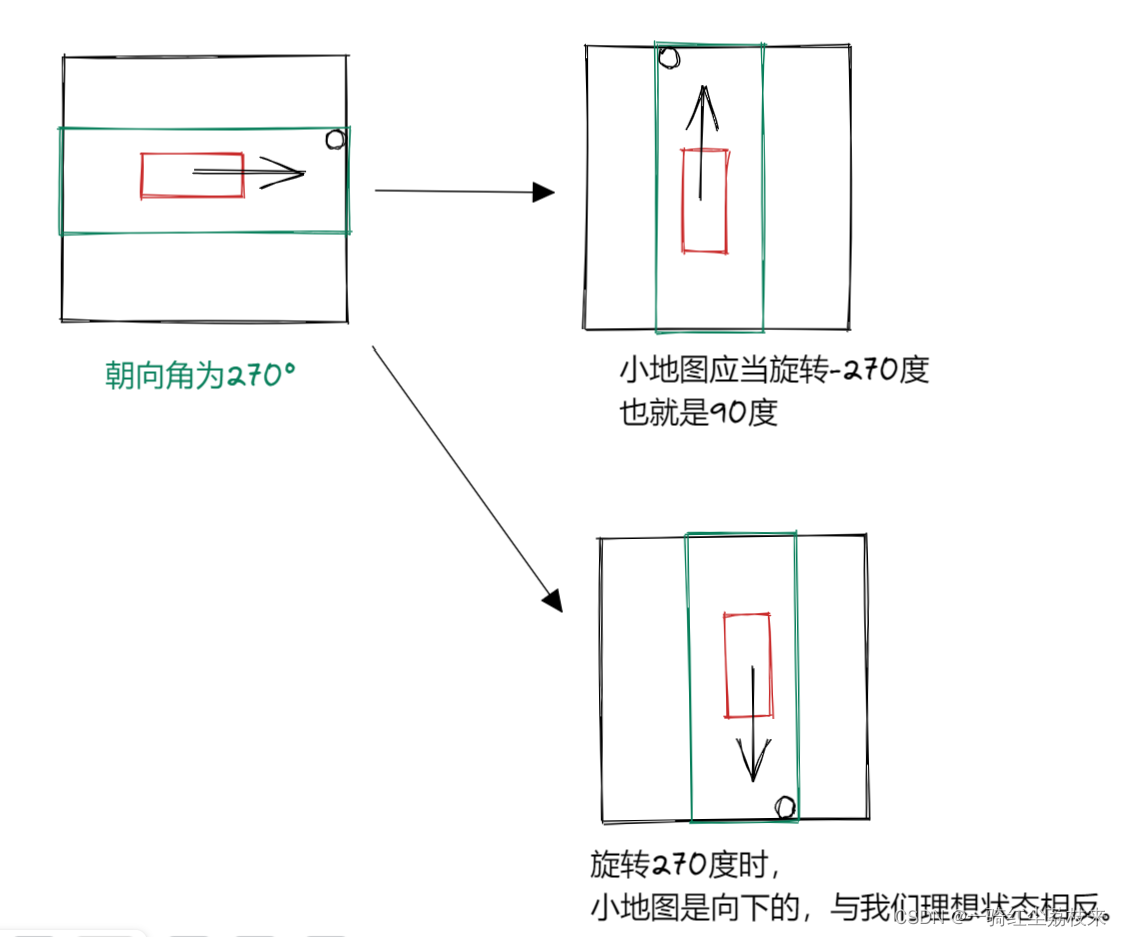
[carla]关于odometry坐标中的角度坐标系 以及 到地图的映射问题
1.获取车辆的Odometry原始信息 在carla中,通过订阅/carla/ego_vecle/odometry 可以查看车辆的全局位置信息,例如: > header: seq: 118872stamp: secs: 5946nsecs: 5720187frame_id: "map" child_frame_id: "ego_vehicle" pos…...

Python 正则表达式
正则表达式主要用来查找和匹配字符串的。 一、正在表达式基础 字符 描述 示例 TIY\ 示意特殊序列(也可用于转义特殊字符)如:空白字符 "\s" . 任何字符(换行符除外) "he..o" ^ 起始于 "^h…...

spark03-读取文件数据分区数量个数原理
代码val conf: SparkConf new SparkConf().setMaster("local").setAppName("wordcount")val sc: SparkContext new SparkContext(conf)val rdd: RDD[String] sc.textFile("datas/1.txt",2)rdd.saveAsTextFile("output")数据格式 &a…...
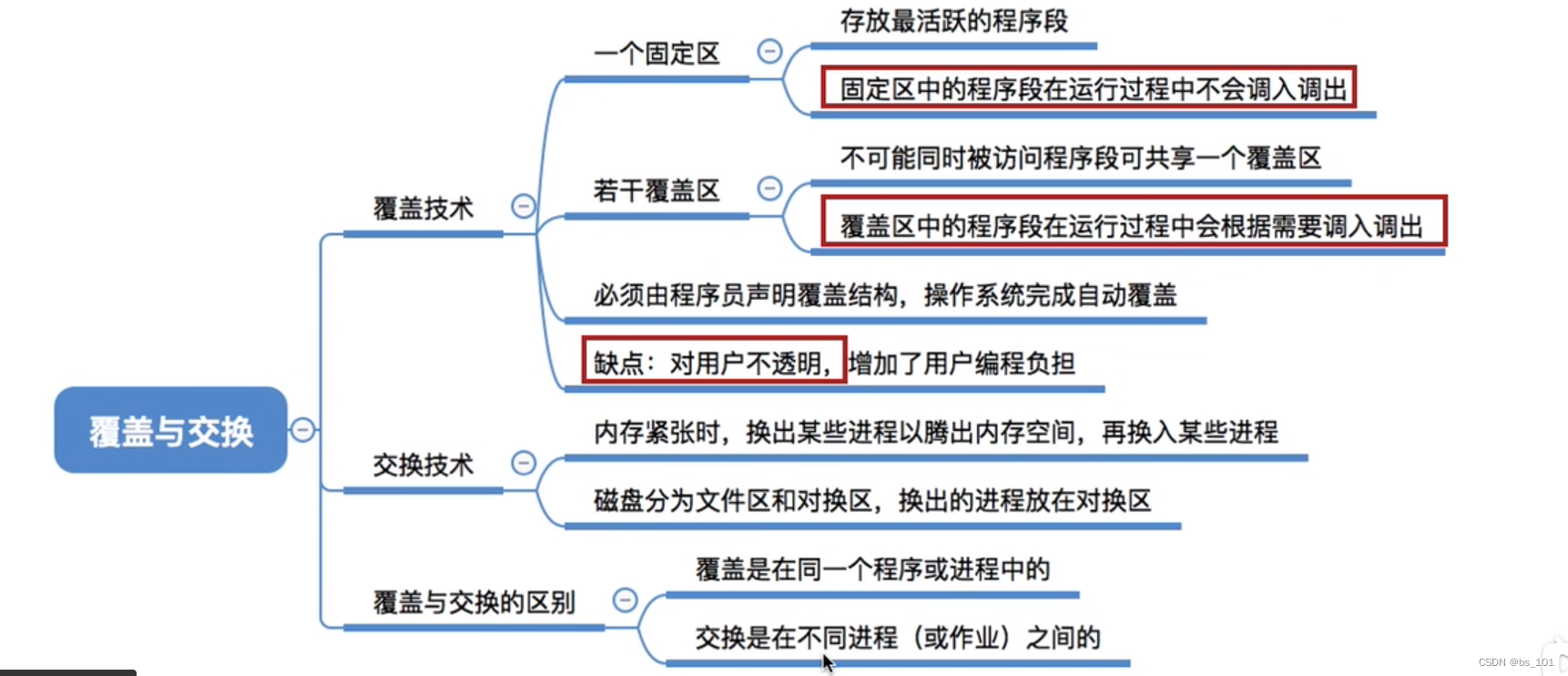
操作系统(day08)内存
存储单元 内存的几个基本概念 存储单元 内存地址从0开始,每个地址对应一个存储单元 存储单元大小根据计算机按照什么方式编址 按字节编址 则每个存储单元大小为一字节,即1B,即8个二进制位按字编址 看这个计算的字长是多少位,如…...
11- 聚类算法 (KMeans/DBSCAN/agg) (机器学习)
聚类算法 聚类算法和降维算法那都属于无监督算法。KMeans 是以一个值为中心, 然后所有其他点到该点距离最小值的累积和。 kmeans KMeans(n_clusters3) # n_clusters 分类数量 kmeans.fit(data.iloc[:,1:]) # 无监督,只需要给数据X就可以 DBSCAN 算法是…...

日日顺供应链|想要看清供应链发展趋势,先回答这三个问题
技术变革如何支撑供应链及管理服务的发展? 数字化与科技化开始承托供应链管理能力的升级与变革? 如何从客户需求的纬度反推供应链及管理服务的模式变革?在过去的三年中,我国的供应链企业经受了最为极端的挑战,但当下&a…...

5守护进程与线程
进程组 多个进程的集合,第一个进程就是组长,组长进程的PID等于进程组ID。 进程组生存期:进程组创建到最后一个进程离开(终止或转移到另一个进程组)。与组长进程是否终止无关。 一个进程可以为自己或子进程设置进程组 ID 相关函数 pid_t …...
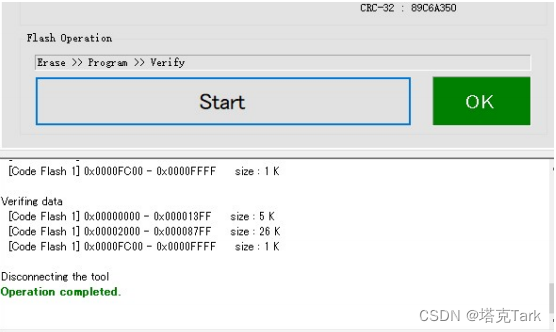
EZ-Cube简易款下载器烧写使用方法
一、硬件连接 跟目标芯片接4根线 VCC、GND、TOOL、REST 四根线,如果板子芯片自己外接电源的,VCC 线可以不接。 二、 安装烧写软件和驱动 烧写软件:https://download.csdn.net/download/Stark_/87444744?spm1001.2014.3001.5503 驱动程序&a…...
sql server安装并SSMS连接
博主简介:原互联网大厂tencent员工,网安巨头Venustech员工,阿里云开发社区专家博主,微信公众号java基础笔记优质创作者,csdn优质创作博主,创业者,知识共享者,欢迎关注,点赞ÿ…...

Python_pytorch (二)
python_pytorch 小土堆pytotch学习视频链接 from的是一个个的包(package) import 的是一个个的py文件(file.py) 所使用的一般是文件中的类(.class) 第一步实例化所使用的类,然后调用类中的方法(def) Torchvision 数据集 数据集使用(CI…...
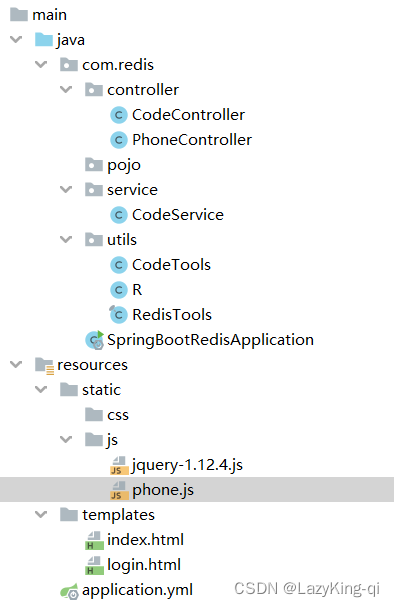
java手机短信验证,并存入redis中,验证码时效5分钟
目录 1、注册发送短信账号一个账号 2、打开虚拟机,将redis服务端打开 3、创建springboot工程,导入相关依赖 4、写yml配置 5、创建controller层,并创建controller类 6、创建service层,并创建service类 7、创建工具类&#x…...

kubectl命令控制远程k8s集群(Windows系统、Ubuntu系统、Centos系统)
文章目录1. 本地是linux2. 本地是Windows1. 本地是linux 安装kubectl命令 法一:从master的/usr/bin目录下拷贝kubectl文件到本机/usr/bin目录下法二:GitHub下载kubectl文件 在家目录下创建.kube目录config文件 法一:将master上对应用户的~/.…...
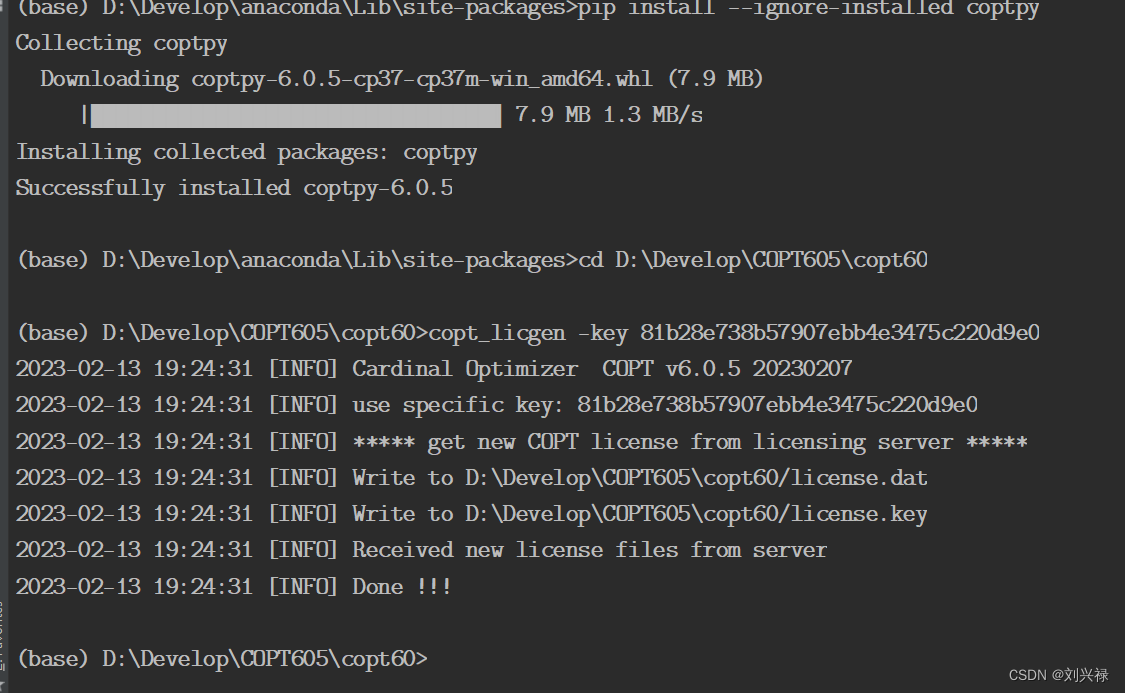
【求解器-COPT】COPT的版本更新中,老版本不能覆盖的问题
【求解器-COPT】COPT的版本更新中,老版本不能覆盖的问题方法1方法2如果license还是找不到作者:刘兴禄 参考网址: COPT的下载和配置步骤如下: 教程 | Windows系统下如何安装COPT求解器并配置许可文件: https://zhuan…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
