当前位置： 首页 > news >正文

nvm控制node版本

news 2026/2/7 21:06:41

安装 nvm

1、下载 nvm

官网安装包： github

选择 nvm-setup.exe 下载

 

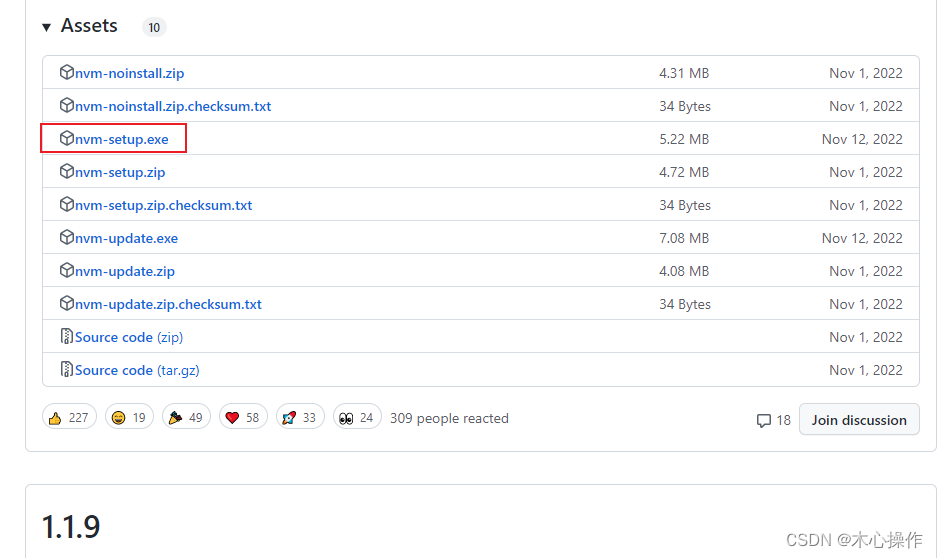
2、安装

1、选择 nvm 安装目录（可自定义）

2、选择 node 安装目录（如有安装过，可以选择以前安装目录，可 cdm 输入 where node 查看原node安装目录）

 3、验证安装

nvm -v

 

安装 node

1、查看 node 版本号

nvm ls available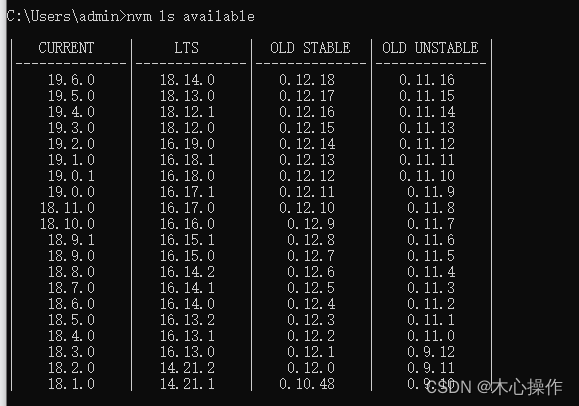

若报错：Could not retrieve https://nodejs.org/dist/latest/.....
则打开 nvm 的安装目录，打开 settings.txt 文件，增加2行，然后保存

node_mirror:https://npm.taobao.org/mirrors/node/
npm_mirror:https://npm.taobao.org/mirrors/npm/

 2、安装 node

nvm install <node版本号>

 3、查看已安装

nvm ls

 * 代表当前使用版本

nvm 常用命令

nvm ls ：列出所有已安装的 node 版本nvm ls-remote ：列出所有远程服务器的版本（官方node version list）nvm list ：列出所有已安装的 node 版本nvm list available ：显示所有可下载的版本nvm install stable ：安装最新版 nodenvm install [node版本号] ：安装指定版本 nodenvm uninstall [node版本号] ：删除已安装的指定版本nvm use [node版本号] ：切换到指定版本 nodenvm current ：当前 node 版本nvm alias [别名] [node版本号] ：给不同的版本号添加别名nvm unalias [别名] ：删除已定义的别名nvm alias default [node版本号] ：设置默认版本

注：切换版本时，要使用管理员权限打开 cmd，否则可能报错

相关文章：

nvm控制node版本

安装 nvm 1、下载 nvm 官网安装包&#xff1a; github 选择 nvm-setup.exe 下载 2、安装 1、选择 nvm 安装目录&#xff08;可自定义&#xff09; 2、选择 node 安装目录&#xff08;如有安装过&#xff0c;可以选择以前安装目录&#xff0c;可 cdm 输入 where node 查看原nod…...

编程日记 2023/5/26 21:55:49

从0到1一步一步玩转openEuler--13 openEuler用户组管理

文章目录13.1 创建用户组13.1.1 groupadd命令13.1.2 用户组信息文件13.1.3 创建用户组实例13.2 修改用户组13.2.1 修改GID13.2.2 修改用户组名13.3 删除用户组13.4 将用户加入用户组或从用户组中移除13.5 切换用户组在Linux中&#xff0c;每个普通用户都有一个账户&#xff0c;…...

编程日记 2023/5/22 23:21:16

知不知道什么叫米筐量化？怎么来的？

现在量化市场范围越来越大&#xff0c;各种量化系统也是普遍性的了&#xff0c;不过米匡量化这个开发系统通常是由交易接口的专业开发团队开发的的结果&#xff0c;那么米匡量化的终端又是是怎么开发成功的呢&#xff1f;首先&#xff0c;我们可以从api接口的调用来了解&#x…...

编程日记 2023/5/15 21:28:25

Urho3D 事件Events

在脚本中&#xff0c;子系统通过以下全局财产可用&#xff1a;时间、文件系统、日志、缓存、网络、输入、ui、音频、引擎、图形、渲染器、脚本、控制台、debugHud、数据库。请注意&#xff0c;由于WorkQueue和Profiler的低级性质&#xff0c;它们不可用于脚本。 事件本身不需要…...

编程日记 2023/5/23 16:53:58

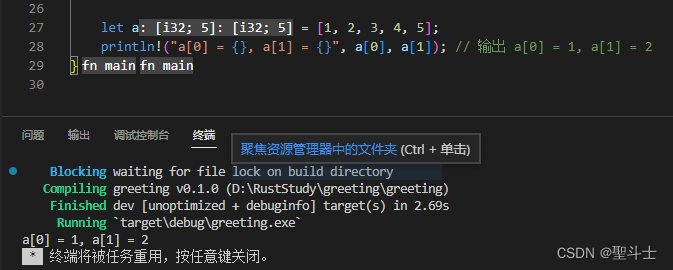
Rust学习入门--【8】复合类型

复合类型&#xff08;compound type&#xff09; 可以将多个不同类型的值组合为一个类型。 Rust中提供了两种内置的复合数据类型&#xff1a;元组&#xff08;tuple&#xff09;和数组&#xff08;array&#xff09;。 元组类型 元组是一个具有 固定长度 的数据集合 —— 无…...

编程日记 2023/5/12 1:32:29

【整理六】

1、props和state相同点和不同点&#xff1f;render方法在哪些情况下会执行&#xff1f; props是一个从外部传进组件的参数&#xff0c;由于React具有单向数据流的特性&#xff0c;所以他的主要作用是从父组件向子组件中传递数据&#xff0c;它是不可改变的&#xff0c;如果想要…...

编程日记 2023/5/30 10:04:01

Ubuntu20.04安装MySQL5.7与远程连接

一、安装MySQL5.7 1.更换镜像源 sudo cp /etc/apt/sources.list /etc/apt/sources.list.old #备份原来的文件 sudo vim /etc/apt/sources.list #修改sources.list文件配置文件内容如下所示&#xff1a; # 清华镜像源 deb https://mirrors.tuna.tsinghua.edu.cn/ubu…...

编程日记 2023/5/24 14:04:28

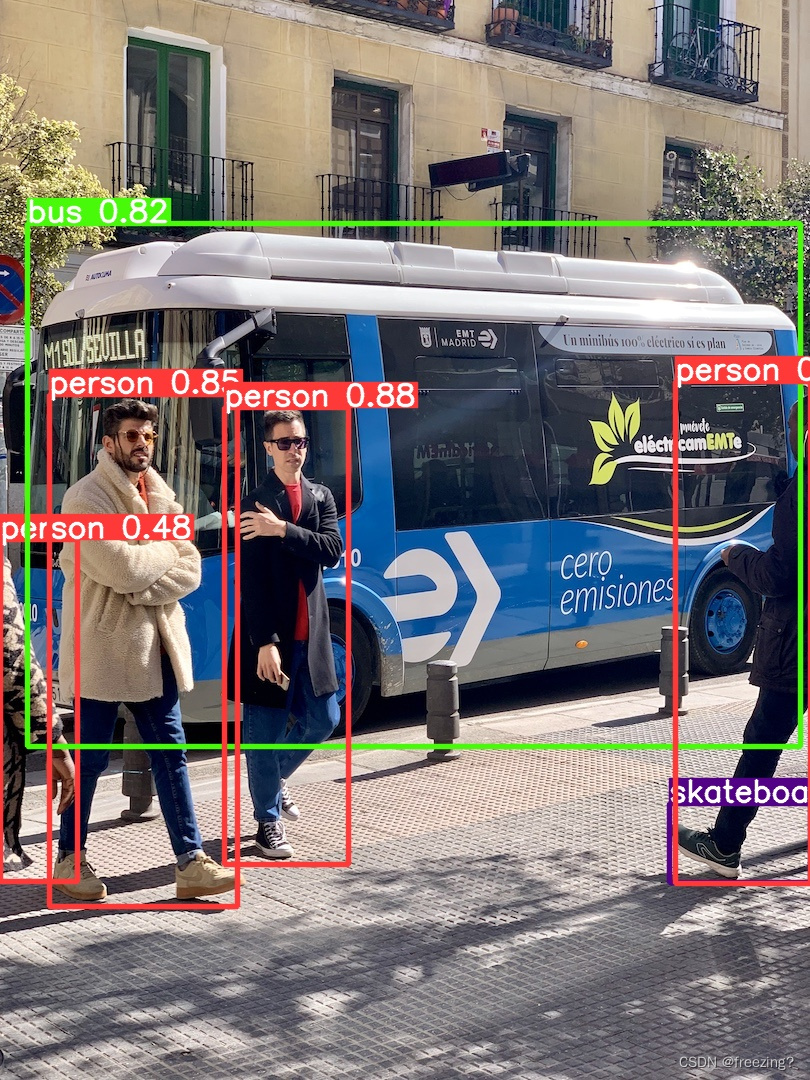
【yolov5】首次尝试目标检测利用prompt（完整操作流程）

1、打开prompt 2、切换到pytorch所在环境 conda activate freezing我的环境名是freezing&#xff0c;这里根据自己环境名去激活切换 3、进入到yolov5项目所在路径 激活完环境后立即执行指令当然是无效的&#xff0c;首先要进入到你的项目目录 首先看一下自己的项目在那个位…...

编程日记 2023/4/18 4:30:42

三大指标继续狂飙！重庆啤酒：不惧强弱分化加剧，深耕高端市场

十多年前&#xff0c;重庆啤酒因为9个跌停而被一片唱衰&#xff0c;资本市场经典的“关灯吃面”典故自此出现&#xff0c;被股民沿用至今。不过自2020年&#xff0c;重庆啤酒开始逆转走势&#xff0c;股价连续上涨。2021年重庆啤酒营收突破百亿大关&#xff0c;净赚11.66亿元&a…...

编程日记 2023/5/14 7:38:57

MySQL数据库14——更新和删除数据

SQL里面使用UPDATE更新数据&#xff0c;删除使用DELETE语句。 Mysql要修改一下设置&#xff0c;才能更新&#xff1a; 在左上角菜单栏里面选择偏好栏&#xff0c;取消下面这个红框的勾选 更新单个字段的数据 如果运行环境为MySQL 则使用以下语句进行备份。 CREATE TABLE stu…...

编程日记 2023/5/14 7:40:33

Java面试——MyBatis篇

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…...

编程日记 2023/5/12 20:20:30

C++的 new 和 delete

文章目录一、new 和 delete 的使用二、operator new 和 operator delete 函数三、new 和 delete 的实现原理四、申请空间和释放空间应配套使用五、定位 new 表达式六、malloc/free 和 new/delete 的区别C语言的动态内存管理函数(malloc、calloc、realloc、free) 虽然可以继续在…...

编程日记 2023/5/30 10:05:15

MySQL 事务原理

文章目录1、事务1.1、ACID 特性1.1.1、原子性undo log1.1.2、一致性1.1.3、* 隔离性1.1.4、持久性redo log1.2、事务控制语句2、隔离级别2.1、隔离级别的分类2.1.1、读未提交 RU2.1.2、读已提交 RC2.1.3、可重复读 RR2.1.4、串行化 SC2.2、并发事务读异常2.2.1、* 脏读2.2.2、*…...

编程日记 2023/4/16 3:27:43

软件测试面试自我介绍/项目介绍居然还有模板？我要是早点发现就好了

目录 1、自我介绍 2、项目介绍 2.1、最全电商项目介绍 2.2、电商项目介绍 2.3、在线教育项目介绍 2.4、互联网金融项目介绍 总结 1、自我介绍 以XXX简历来举例&#xff08;参照下面的案例&#xff0c;编写你的自我介绍&#xff0c;框架就是&#xff1a;我是谁&#xff0…...

编程日记 2023/5/14 18:13:26

new RegExp的使用

1.RegExp是什么 当检索某个文本时&#xff0c;可以使用一种模式来描述要检索的内容。RegExp 就是这种模式 RegExp 对象用于存储检索模式。 var patt1new RegExp("e");当使用该 RegExp 对象在一个字符串中检索时&#xff0c;将寻找的是字符 “e” g &#xff1a;表…...

编程日记 2023/4/17 4:38:24

供应商管理软件如何选型 好用的供应商管理软件推荐

供应商管理是采购中的重要环节。对于很多企业来说&#xff0c;做好内部供应商管理就能在行业竞争中提升自身的效益与竞争能力&#xff0c;供应商已成为一种战略筹码。 但在企业进行供应商管理过程中&#xff0c;往往会遇到供应商信息数据收集不全、等级划分不合理、绩效评价机…...

编程日记 2023/5/29 8:36:41

Python3遍历文件夹提取关键字及其附近字符

要求&#xff1a; 1&#xff0c;遍历文件夹下所有的.xml文件 2&#xff0c;从.xml文件中提取关键字以及左右十个字符 3&#xff0c;输出到excel 一&#xff1a;遍历文件夹找到所有xml文件及其路径 for root, dirs, files in os.walk(self.inputFilePath):for file in files:…...

编程日记 2023/5/22 23:24:09

「1」线性代数（期末复习）

&#x1f680;&#x1f680;&#x1f680;大家觉不错的话&#xff0c;就恳求大家点点关注&#xff0c;点点小爱心&#xff0c;指点指点&#x1f680;&#x1f680;&#x1f680; 第一章 行列式 行列式是一个数&#xff0c;是一个结果三阶行列式的计算&#xff1a;主对角线的乘…...

编程日记 2023/5/28 19:55:11

C++7：STL-模拟实现vector

目录 vector的成员变量 构造函数 reserve size() capacity() push_back 一些小BUG 赋值操作符重载 析构函数 【】操作符重载 resize pop_back Insert 迭代器失效 erase 二维数组问题 总结一下 vector&#xff0c;翻译软件会告诉你它的意思是向量&#xff0c;但其…...

编程日记 2023/5/12 0:52:12

笑死，面试官又问我SpringBoot自动配置原理

面试官&#xff1a;好久没见&#xff0c;甚是想念。今天来聊聊SpringBoot的自动配置吧&#xff1f; 候选者&#xff1a;嗯&#xff0c;SpringBoot的自动配置我觉得是SpringBoot很重要的“特性”了。众所周知&#xff0c;SpringBoot有着“约定大于配置”的理念&#xff0c;这一…...

编程日记 2023/5/22 23:25:42

云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？

大家好&#xff0c;欢迎来到《云原生核心技术》系列的第七篇&#xff01; 在上一篇&#xff0c;我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在&#xff0c;我们就像一个拥有了一块崭新数字土地的农场主&#xff0c;是时…...

编程新知 2025/12/14 22:32:59

Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）

概述 在 Swift 开发语言中&#xff0c;各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过&#xff0c;在涉及到多个子类派生于基类进行多态模拟的场景下&#xff0c;…...

编程新知 2026/1/23 4:56:05

网络编程（UDP编程）

思维导图 UDP基础编程&#xff08;单播&#xff09; 1.流程图 服务器&#xff1a;短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

编程新知 2026/2/4 17:31:44

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2026/1/28 4:50:33

uniapp 开发ios， xcode 提交app store connect 和 testflight内测

uniapp 中配置 配置manifest 文档&#xff1a;manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号&#xff1a;4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

编程新知 2026/1/31 8:35:07

tomcat入门

1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效&#xff0c;稳定&#xff0c;易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

编程新知 2025/7/7 19:44:31

nnUNet V2修改网络——暴力替换网络为UNet++

更换前，要用nnUNet V2跑通所用数据集，证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构，初步了解要修改的网络，知己知彼，修改起来才能游刃有余。 U-Net存在两个局限，一是网络的最佳深度因应用场景而异，这取决于任务的难度和可用于训练的标注数…...

编程新知 2026/2/7 10:22:16

MFE(微前端) Module Federation：Webpack.config.js文件中每个属性的含义解释

以Module Federation 插件详为例&#xff0c;Webpack.config.js它可能的配置和含义如下&#xff1a; 前言 Module Federation 的Webpack.config.js核心配置包括&#xff1a; name filename&#xff08;定义应用标识&#xff09; remotes&#xff08;引用远程模块&#xff0…...

编程新知 2025/9/20 11:57:48

MySQL的pymysql操作

本章是MySQL的最后一章&#xff0c;MySQL到此完结&#xff0c;下一站Hadoop&#xff01;&#xff01;&#xff01; 这章很简单&#xff0c;完整代码在最后&#xff0c;详细讲解之前python课程里面也有&#xff0c;感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

编程新知 2026/1/20 12:20:43

TCP/IP 网络编程 | 服务端 客户端的封装

设计模式 文章目录 设计模式一、socket.h 接口&#xff08;interface&#xff09;二、socket.cpp 实现&#xff08;implementation&#xff09;三、server.cpp 使用封装&#xff08;main 函数&#xff09;四、client.cpp 使用封装&#xff08;main 函数&#xff09;五、退出方法…...

编程新知 2025/7/27 7:26:07