Python - 数字(Number)数据类型常用操作
目录
- 数字运算
- 类型转换
- 数学函数
- 数学库math、cmath
- math 模块常量
- math 模块方法
- 随机函数库 random
- random 模块方法
- 保留小数到指定位数
- 三角函数
数字运算
=:用于给变量赋值type(x):查看数据所属类型isinstance(x, A_tuple):判断数据是否为预期类型+:两个数相加-:两个数相减*:两个数相乘/:两个数相除%:两个数进行求余**:两个数进行幂运算
# 给变量赋值数字类型数据
int_data = 100 # 整数 int
float_data = 8.88 # 小数 float
complex_data = 3+5j # 复数 complex# 查看变量所属数据类型
print(type(int_data)) # <class 'int'>
print(type(float_data)) # <class 'float'>
print(type(complex_data)) # <class 'complex'># 判断两个数据的类型是否相等
print(isinstance(int_data, int)) # True
print(isinstance(float_data, int)) # False# 加
print(2 + 1) # 3
print(2 + 6.6) # 8.6 整数和浮点数运算结果为浮点数
print(2.1 + 1.2) # 3.3# 减
print(2 - 1) # 1
print(2 - 6.6) # -4.6
print(2.1 - 1.2) # 0.9000000000000001
print(round(2.1 - 1.2, 1)) # 0.9# 乘
print(2 * 1) # 2
print(2 * 6.6) # 13.2
print(2.1 * 1.2) # 2.52# 除
print(2 / 1) # 2.0
print(6.66 / 2) # 3.33
print(6.66 / 2.22) # 3.0# 求余
print(10 % 3) # 1
print(20.22 % 3) # 2.219999999999999# 幂运算
print(5 ** 2) # 5的平方,25
print(2 ** 7) # 2的7次方,128
类型转换
int(x, base=10):将一个字符串或数字转换为整型。x为字符串或数字,base为进制数,默认10进制。float(x):将一个字符串或数字转换为浮点数。x为字符串或整数。
# int()
# 不传参数则为0
int() # 0
# 将字符串转为整数
int("666") # 666
# 向下取整
int(6.66) # 6
# 将数字转为8进制
int('12',8) # 10# flaot()
# 不传参数则为0.0
flaot() # 0.0
# 将字符串转为浮点数
float("6.88") # 6.88
注意:如果转换内容中出现非数字字符则会报错。
数学函数
| 函数 | 说明 |
|---|---|
abs(x) | 返回数字的绝对值。x为数值表达式。 |
max(x) | 返回给定参数的最大值,参数可以为序列。 |
min(x) | 返回给定参数的最小值,参数可以为序列。 |
pow(x, y, z) | 返回x的y次方的值。如果z存在则对结果进行取模,等效于pow(x,y) %z |
round(number, digits) | 返回number保留digits位四舍五入的小数,digits不填默认为保留整数 |
使用示例:
abs(-2.66) # 2.66max(1, 2, 3) # 3
max([6, 7, 8]) # 8min(1, 2, 3) # 1pow(10,2) # 100
pow(10,2,3) # 1round(5.68) # 6
round(5.64, 1) # 5.6
数学库math、cmath
math:模块提供了许多对浮点数的数学运算函数。cmath:模块包含了一些用于复数运算的函数。
查看math中包含的内容:
import mathprint(dir(math))# 打印内容
['__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc'
]
math 模块常量
| 常量 | 说明 |
|---|---|
math.e | 返回欧拉数 (2.7182…) |
math.inf | 返回正无穷大浮点数 |
math.nan | 返回一个浮点值 NaN (not a number) |
math.pi | π 一般指圆周率。 圆周率 PI (3.1415…) |
math.tau | 数学常数 τ = 6.283185…,精确到可用精度。Tau 是一个圆周常数,等于 2π,圆的周长与半径之比。 |
math 模块方法
| 函数 | 说明 |
|---|---|
math.acos(x) | 返回 x 的反余弦,结果范围在 0 到 pi 之间。 |
math.acosh(x) | 返回 x 的反双曲余弦值。 |
math.asin(x) | 返回 x 的反正弦值,结果范围在 -pi/2 到 pi/2 之间。 |
math.asinh(x) | 返回 x 的反双曲正弦值。 |
math.atan(x) | 返回 x 的反正切值,结果范围在 -pi/2 到 pi/2 之间。 |
math.atan2(y, x) | 返回给定的 X 及 Y 坐标值的反正切值,结果是在 -pi 和 pi 之间。 |
math.atanh(x) | 返回 x 的反双曲正切值。 |
math.ceil(x) | 将 x 向上舍入到最接近的整数 |
math.comb(n, k) | 返回不重复且无顺序地从 n 项中选择 k 项的方式总数。 |
math.copysign(x, y) | 返回一个基于 x 的绝对值和 y 的符号的浮点数。 |
math.cos() | 返回 x 弧度的余弦值。 |
math.cosh(x) | 返回 x 的双曲余弦值。 |
math.degrees(x) | 将角度 x 从弧度转换为度数。 |
math.dist(p, q) | 返回 p 与 q 两点之间的欧几里得距离,以一个坐标序列(或可迭代对象)的形式给出。 两个点必须具有相同的维度。 |
math.erf(x) | 返回一个数的误差函数 |
math.erfc(x) | 返回 x 处的互补误差函数 |
math.exp(x) | 返回 e 的 x 次幂,Ex, 其中 e = 2.718281… 是自然对数的基数。 |
math.expm1() | 返回 Ex - 1, e 的 x 次幂,Ex,其中 e = 2.718281… 是自然对数的基数。这通常比 math.e ** x 或 pow(math.e, x) 更精确。 |
math.fabs(x) | 返回 x 的绝对值。 |
math.factorial(x) | 返回 x 的阶乘。 如果 x 不是整数或为负数时则将引发 ValueError。 |
math.floor() | 将数字向下舍入到最接近的整数 |
math.fmod(x, y) | 返回 x/y 的余数 |
math.frexp(x) | 以 (m, e) 对的形式返回 x 的尾数和指数。 m 是一个浮点数, e 是一个整数,正好是 x == m * 2**e 。 如果 x 为零,则返回 (0.0, 0) ,否则返回 0.5 <= abs(m) < 1 。 |
math.fsum(iterable) | 返回可迭代对象 (元组, 数组, 列表, 等)中的元素总和,是浮点值。 |
math.gamma(x) | 返回 x 处的伽马函数值。 |
math.gcd() | 返回给定的整数参数的最大公约数。 |
math.hypot() | 返回欧几里得范数,sqrt(sum(x**2 for x in coordinates))。 这是从原点到坐标给定点的向量长度。 |
math.isclose(a,b *,rel_tol=1e-09,abs_tol=0.0) | 检查两个值是否彼此接近,若 a 和 b 的值比较接近则返回 True,否则返回 False。 |
math.isfinite(x) | 判断 x 是否有限,如果 x 既不是无穷大也不是 NaN,则返回 True ,否则返回 False 。 |
math.isinf(x) | 判断 x 是否是无穷大,如果 x 是正或负无穷大,则返回 True ,否则返回 False 。 |
math.isnan() | 判断数字是否为 NaN,如果 x 是 NaN(不是数字),则返回 True ,否则返回 False 。 |
math.isqrt() | 将平方根数向下舍入到最接近的整数。 |
math.ldexp(x, i) | 返回 x * (2**i) 。 这基本上是函数 math.frexp() 的反函数。 |
math.lgamma() | 返回伽玛函数在 x 绝对值的自然对数。 |
math.log(x[, base]) | 使用一个参数,返回 x 的自然对数(底为 e )。 |
math.log10(x) | 返回 x 底为 10 的对数。 |
math.log1p(x) | 返回 1+x 的自然对数(以 e 为底)。 |
math.log2(x) | 返回 x 以 2 为底的对数 |
math.perm(n, k=None) | 返回不重复且有顺序地从 n 项中选择 k 项的方式总数。 |
math.pow(x, y) | 将返回 x 的 y 次幂。 |
math.prod(iterable) | 计算可迭代对象中所有元素的积。 |
math.radians(x) | 将角度 x 从度数转换为弧度。 |
math.remainder(x, y) | 返回 IEEE 754 风格的 x 除于 y 的余数。 |
math.sin(x) | 返回 x 弧度的正弦值。 |
math.sinh(x) | 返回 x 的双曲正弦值。 |
math.sqrt(x) | 返回 x 的平方根。 |
math.tan(x) | 返回 x 弧度的正切值。 |
math.tanh(x) | 返回 x 的双曲正切值。 |
math.trunc(x) | 返回 x 截断整数的部分,即返回整数部分,删除小数部分 |
使用示例:
import mathmath.ceil(5.4) # 6
math.ceil(5.5) # 6math.fabs(-6) # 6.0
math.fabs(6) # 6.0math.floor(6.9) # 6math.fmod(5, 2) # 1.0math.isclose(8.005, 8.450, abs_tol = 0.4) # False
math.isclose(8.005, 8.450, abs_tol = 0.5) # True
print(0.1+0.2) # 0.30000000000000004
math.isclose(0.1+0.2, 0.3) #Truemath.isnan(float("NaN")) # Truemath.pow(2, 10) # 1024.0math.sqrt(25) # 5.0
随机函数库 random
查看random中包含的内容:
import randomprint(dir(random))# 打印内容
['BPF', 'LOG4', 'NV_MAGICCONST', 'RECIP_BPF', 'Random', 'SG_MAGICCONST', 'SystemRandom', 'TWOPI', '_Sequence', '_Set', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_accumulate', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_inst', '_log', '_os', '_pi', '_random', '_repeat', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', '_warn', 'betavariate', 'choice', 'choices', 'expovariate', 'gammavariate', 'gauss', 'getrandbits', 'getstate', 'lognormvariate', 'normalvariate', 'paretovariate', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'shuffle', 'triangular', 'uniform', 'vonmisesvariate', 'weibullvariate'
]
random 模块方法
| 函数 | 说明 |
|---|---|
seed() | 初始化随机数生成器。 |
getstate() | 返回捕获生成器当前内部状态的对象。 |
setstate() | state 应该是从之前调用 getstate() 获得的,并且 setstate() 将生成器的内部状态恢复到 getstate() 被调用时的状态。 |
getrandbits(k) | 返回具有 k 个随机比特位的非负 Python 整数。 此方法随 MersenneTwister 生成器一起提供,其他一些生成器也可能将其作为 API 的可选部分提供。 在可能的情况下,getrandbits() 会启用 randrange() 来处理任意大的区间。 |
randrange() | 从 range(start, stop, step) 返回一个随机选择的元素。 |
randint(a, b) | 返回随机整数 N 满足 a <= N <= b。 |
choice(seq) | 从非空序列 seq 返回一个随机元素。 如果 seq 为空,则引发 IndexError。 |
choices(population, weights=None, *, cum_weights=None, k=1) | 从 population 中选择替换,返回大小为 k 的元素列表。 如果 population 为空,则引发 IndexError。 |
shuffle(x[, random]) | 将序列 x 随机打乱位置。 |
sample(population, k, *, counts=None) | 返回从总体序列或集合中选择的唯一元素的 k 长度列表。 用于无重复的随机抽样。 |
random() | 返回 [0.0, 1.0) 范围内的下一个随机浮点数。 |
uniform(x, y) | 随机生成下一个实数,它在[x,y]范围内。 |
triangular(low, high, mode) | 返回一个随机浮点数 N ,使得 low <= N <= high 并在这些边界之间使用指定的 mode 。 low 和 high 边界默认为零和一。 mode 参数默认为边界之间的中点,给出对称分布。 |
betavariate(alpha, beta) | Beta 分布。 参数的条件是 alpha > 0 和 beta > 0。 返回值的范围介于 0 和 1 之间。 |
expovariate(lambd) | 指数分布。 lambd 是 1.0 除以所需的平均值,它应该是非零的。 |
gammavariate() | Gamma 分布( 不是伽马函数) 参数的条件是 alpha > 0 和 beta > 0。 |
gauss(mu, sigma) | Gamma 分布( 不是伽马函数) 参数的条件是 alpha > 0 和 beta > 0。 |
lognormvariate(mu, sigma) | 对数正态分布。 如果你采用这个分布的自然对数,你将得到一个正态分布,平均值为 mu 和标准差为 sigma 。 mu 可以是任何值,sigma 必须大于零。 |
normalvariate(mu, sigma) | 正态分布。 mu 是平均值,sigma 是标准差。 |
vonmisesvariate(mu, kappa) | 冯·米塞斯分布。 mu 是平均角度,以弧度表示,介于0和 2*pi 之间,kappa 是浓度参数,必须大于或等于零。 |
paretovariate(alpha) | 帕累托分布。 alpha 是形状参数。 |
weibullvariate(alpha, beta) | 威布尔分布。 alpha 是比例参数,beta 是形状参数。 |
使用示例:
import random# 从1-100中选一个整数
print(random.randint(1,100)) # 80print(random.choice([1, 2, 3, 5, 9])) # 2
print(random.choice('A String')) # A
print(random.choice(range(10))) # 8# 从 1-100 中选取一个奇数
print(random.randrange(1, 100, 2)) # 57
# 从 0-99 选取一个随机数
print(random.randrange(100)) # 91
# 随机选取0到100间的偶数
print(random.randrange(0, 101, 2)) # 22print(random.random()) # 0.699045676948276print(random.uniform(1, 100)) # 66.79353123577998
保留小数到指定位数
# 向下取整,转为整数
print(int(58.86)) # 58import math
# 向上取整,转为整数
print(math.ceil(58.86)) # 59# 四舍五入,转为整数
print(round(58.86)) # 59# 四舍五入,保留2位小数
print(round(4.859999999999999, 2)) # 4.86# 分割整数和小数
print(str(58.866).split(".")[0]) # 58
三角函数
| 函数 | 说明 |
|---|---|
acos(x) | 返回x的反余弦弧度值。 |
asin(x) | 返回x的反正弦弧度值。 |
atan(x) | 返回x的反正切弧度值。 |
atan2(y, x) | 返回给定的 X 及 Y 坐标值的反正切值。 |
cos(x) | 返回x的弧度的余弦值。 |
hypot(x, y) | 返回欧几里德范数 sqrt(xx + yy)。 |
sin(x) | 返回的x弧度的正弦值。 |
tan(x) | 返回x弧度的正切值。 |
degrees(x) | 将弧度转换为角度,如degrees(math.pi/2) , 返回90.0。 |
radians(x) | 将角度转换为弧度。 |
相关文章:
数据类型常用操作)
Python - 数字(Number)数据类型常用操作
目录数字运算类型转换数学函数数学库math、cmathmath 模块常量math 模块方法随机函数库 randomrandom 模块方法保留小数到指定位数三角函数数字运算 :用于给变量赋值type(x):查看数据所属类型isinstance(x, A_tuple):判断数据是否为预期类型…...
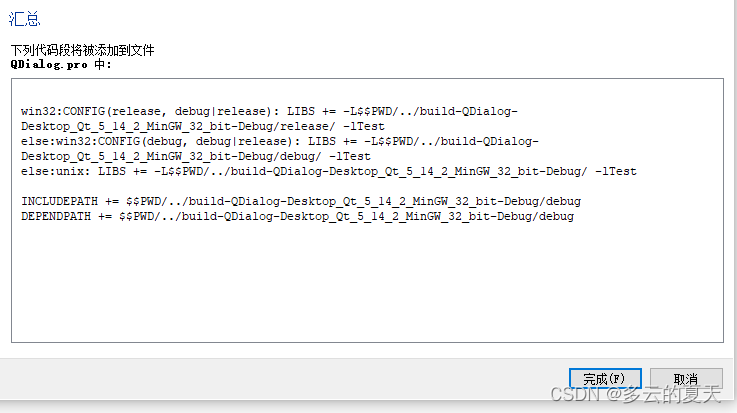
QT(51)-动态链接库-windows
1.qt- 调用win32 DLL 2.qt- 调用MFC DLL 0概述: 01.扩展DLL: 必须有一个DllMain()函数,且调用AfxInitExtensionModule()函数。 CRuntimeClass类-初始化函数CDynLinkLibrary。02.windows定位DLL文件: 1)…...
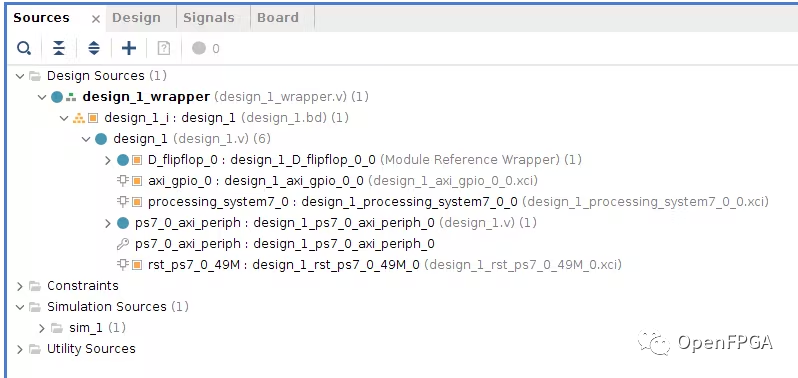
[Vivado那些事儿]将自定义 IP (HDL)添加到 Vivado 模块设计(Block Design)
绪论使用Vivado Block Design设计解决了项目继承性问题,但是还有个问题,不知道大家有没有遇到,就是新设计的自定义 RTL 文件无法快速的添加到Block Design中,一种方式是通过自定义IP,但是一旦设计的文件有问题就需要重…...

开学必备数码清单,大学生开学必备数码好物分享
还有很多小伙伴不知道开学应该准备什么,在学校当中需要用到的数码产品,在宿舍娱乐使用的音箱、学习当中使用到的笔记本,这些都是我们可以准备的,还有一个小众的好物,能够让我们在学校当中提升生活的幸福感,…...

【面试题】常见前端基础面试题(HTML,CSS,JS)
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库html语义化的理解代码结构: 使页面在没有css的情况下,也能够呈现出好的内容结构有利于SEO: 爬虫根据标签来分配关键字的权重,因此可以和搜索引擎…...
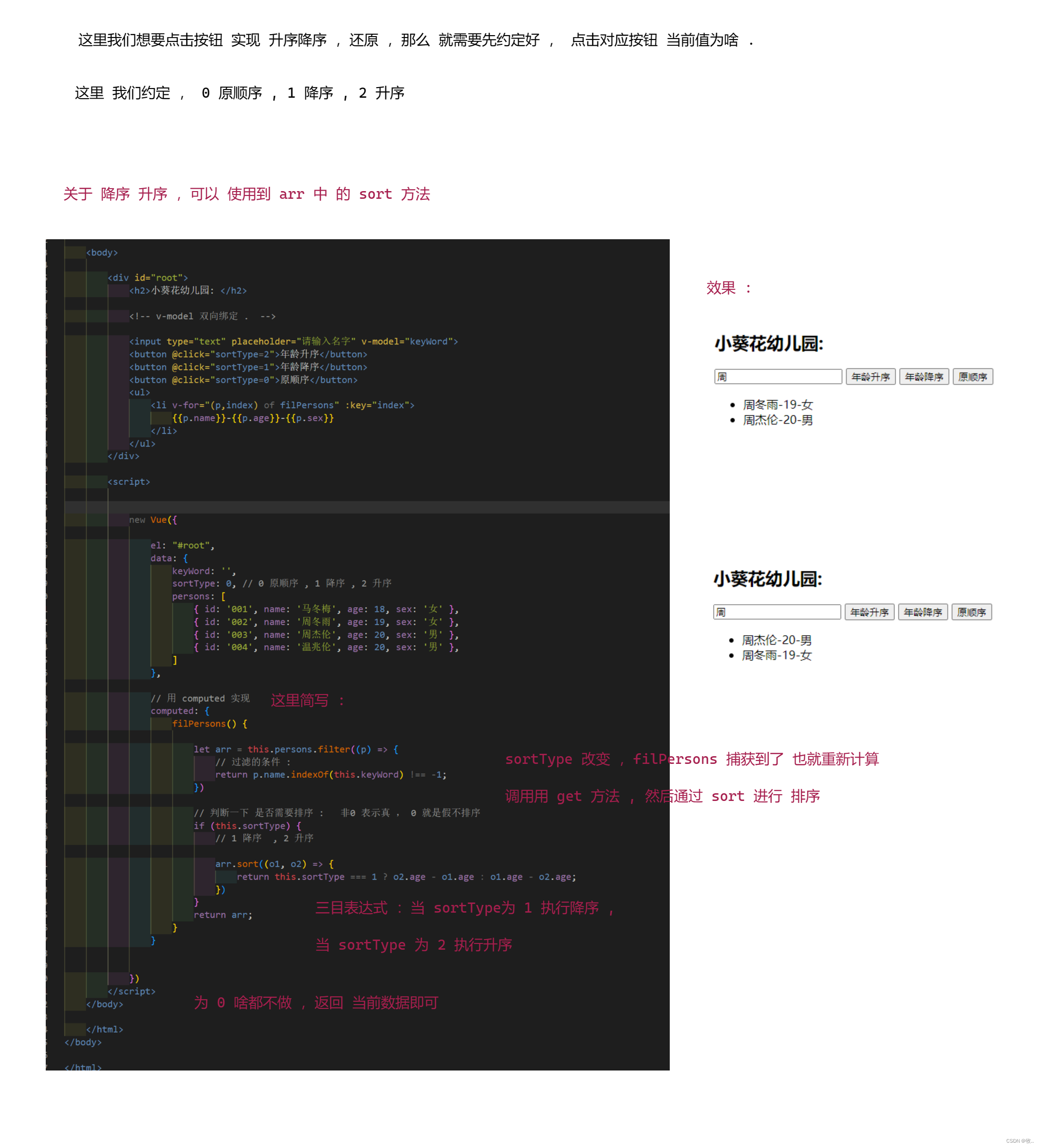
Vue (4)
文章目录1. 绑定样式1.1 绑定 class 样式1.2 绑定 style 样式2. 条件渲染2.1 v-show2.2 v-if3. 列表渲染3.1 v-for3.2 key 的作用与原理3.3 列表过滤3.4 列表排序1. 绑定样式 说 绑定样式 前,先准备好 以下几个 样式 : <style>.basic {width: 400px;height: 1…...
静态库和动态库的制作
一、什么叫做库: 库:二进制的程序,能被操作系统载入内存中执行 二、Linux下的库有两种:静态库和共享库(动态库),二者的不同点在于代码载入的时刻不同。 A、静态库在程序编译的时候并会被连接到目标代码中,程…...
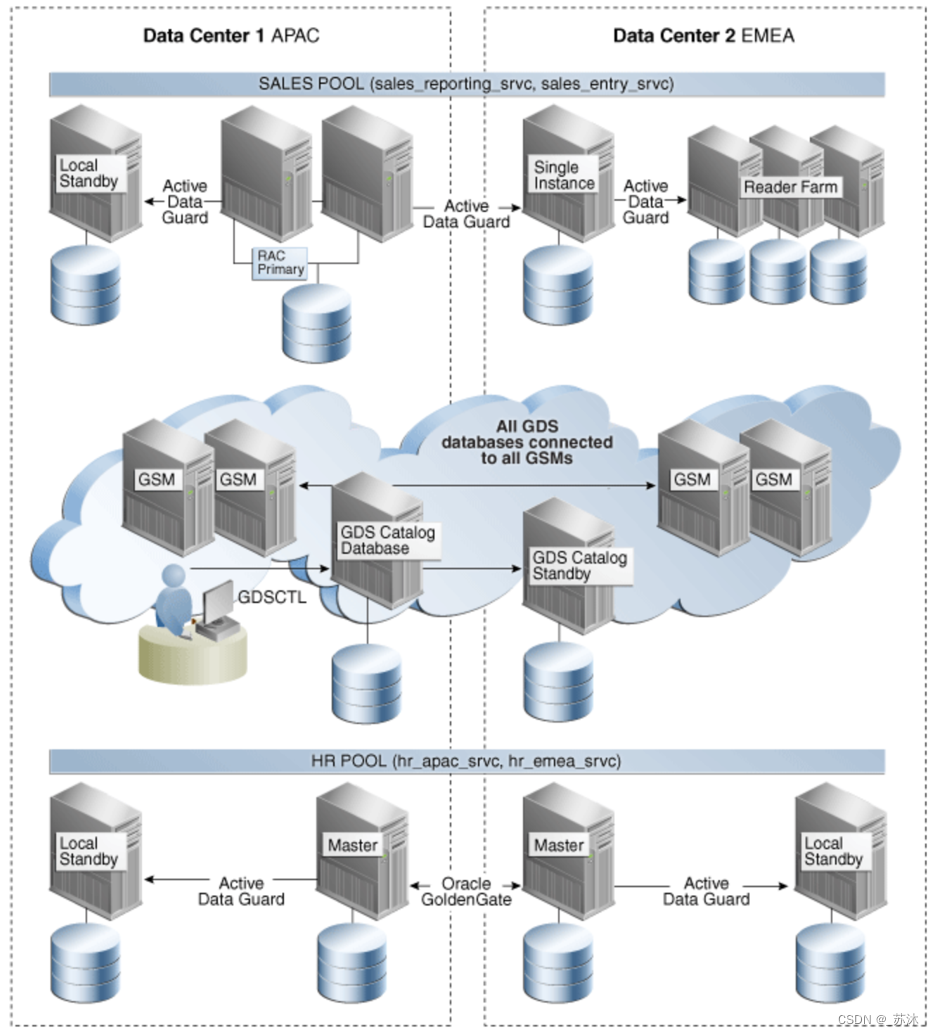
Oracle实现高可用性的工具(负载均衡/故障切换)
Oracle实现高可用性的工具(负载均衡/故障切换)1 Oracle RAC故障转移负载均衡2 Data Guard负载均衡-读写分离Data Guard Broker3 GDSGSM:连接管理工具主要功能Data Guard Broker功能是监控Data Guard状态,当主库异常时自动切换角色…...
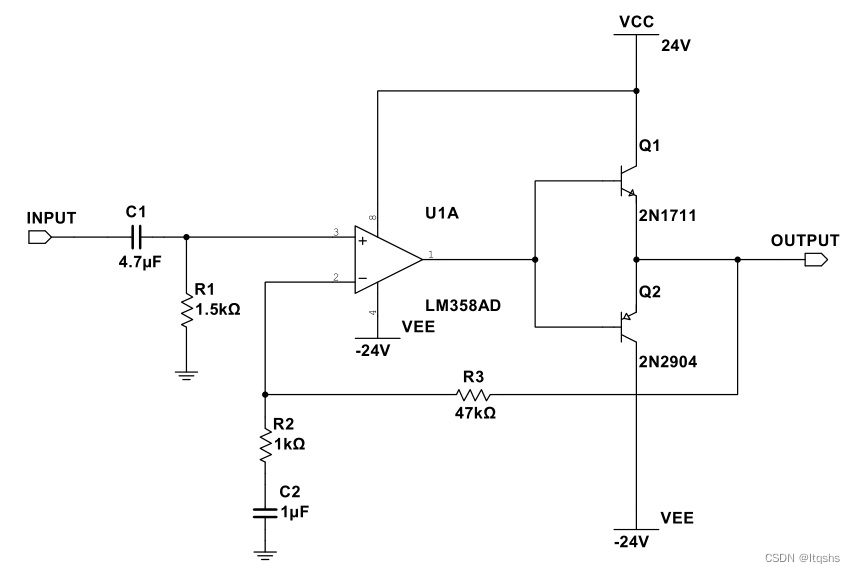
图解经典电路之OCL差分功放-三极管分立器件电路分析
下面从简到繁,从框架到细节的顺序讲解电路。即先讲框架,然后逐渐添加电路细节,所以大家跟上思路。 1、第一步,尽可能的抽象这个电路,等效如下: 图二 OCL等效电路 整个OCL电路,可以等效为一个大功率的运放,加上几个电阻电容构成了一个同向放大器,就是这么简单。 为了便…...

thymeleaf模板注入学习与研究--查找与防御
一、日常编码中常见的两种漏洞场景 1.1 模板参数外部可控 RequestMapping("/path")public String path(RequestParam String lang) {return lang ;}实际开发过程中 依靠我丰富的想象力只能想出 换主题 这种场景下可能会出现 大佬们自行脑补吧。 1.2 使用GetMappin…...
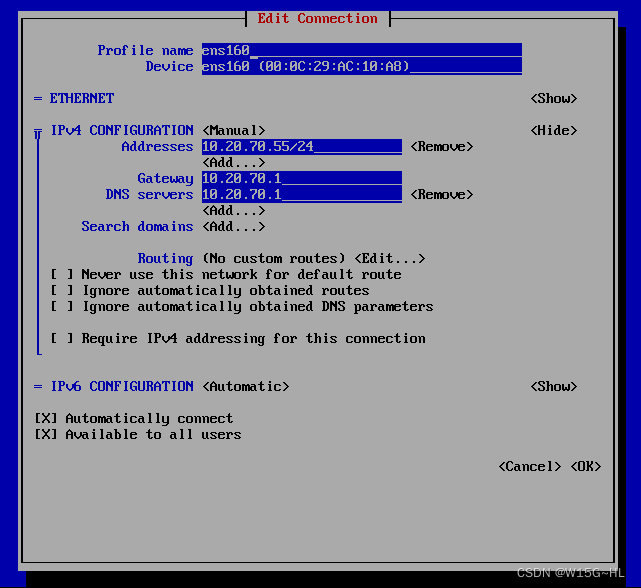
第七章:Linux最小化搭建环境解说2
配置IP地址:我们先要到网卡配置文件夹里,路径是/etc/sysconfig/network-scripts/,有点长,不过没事,我们要学会习惯,这还是经常用的。然后就是用ls命令查看下面有什么,只有一个文件ifcfg-ens160&…...

两道链表经典算法题---链表有无环(基础+进阶)
生活就像一盒巧克力,你永远不知道你会得到什么。——《阿甘正传》目前自己粗略的学完数据结构,正在开始刷算法题目。个人觉得算法是一个积累,循序渐进的的过程,需要不断加量,进而达到所谓的质。链表作为数据结构一个重…...

2023/1/14总结
今天学习的是c语法知识。 容器arry: 通俗来说这个容器就i是c语言的数组,和C中vevtor不同,arry是定长度的,而vector是动态数组。头文件为:<arry> 初始化: arry<数据类型,你所要声明…...

Python 之 NumPy 统计函数、数据类型和文件操作
文章目录一、统计函数1. 求平均值 mean()2. 中位数 np.median3. 标准差 ndarray.std4. 方差 ndarray.var()5. 最大值 ndarray.max()6. 最小值 ndarray.min()7. 求和 ndarray.sum()8. 加权平均值 numpy.average()二、数据类型1. 数据存储2. 定义结构化数据3. 结构化数据操作三、…...
互联网新时代要到来了(一)什么是Web3.0?
什么是Web3.0? tips:内容来自百度百科、知乎、搜狐新闻、李留白公众号、CSDN「Meta.Qing」博客等网页 什么是Web3.0?1.什么是Web3.0(概念介绍)?2.Web3.0简单理解3.Web3.0的技术特点4.Web3.0项目1.什么是Web3.0(概念…...

[Yocto] 直接向deploy/images目录部署binary
最近用yocto的时候碰到一个问题,有一些IP的FW binary是从别的地方直接拿来的,没有source code,有一个需求就是需要把它用wks script的方式把它们打包到最后的image里,这篇文章就是来谈谈这个问题。 yocto patch/deploy等做了什么 首先,虽然我们的code,bbfile,或者说pa…...
设备控制开发与实现(二))
HarmonyOS Connect原子化服务功能开发(Wi-Fi/Combo)设备控制开发与实现(二)
规设备控制 在“device”目录下的“DeviceApplication.java”文件中,在onInitialize函数中初始化应用。示例代码如下: Override public void onInitialize() {AiLifeServiceHelper.initApplication(this);DeviceHandlerAbility.register(this, "&qu…...

浅析 Makefile
Makefile逻辑 Makefile就是将一系列的工作流串在一起自动执行,构成Makefile最基本的要素是目标、依赖、命令。也就是为了实现目标需要哪些依赖并执行什么样的命令。 target: dependences1 dependences2 ... command1 command2 ...其中,target表示要生…...

保护品牌线上声誉的5种方法
我们如今生活在一个搜索便捷的世界,对于一个企业和个人来说,品牌的线上声誉也尤为重要。在客户考虑与您的公司开展业务之前,他们理所当然会先使用众多软件和平台搜索相关信息,以帮助他们了解和做决定。 因此,您的品牌…...

Java多重选择结构,超详细整理,适合新手入门
目录 一、什么是多重选择结构? 二、if 语句的语法 1、什么是嵌套if语句? 2、if 语句循环基本用法: 3、案例: 二、if...else多重选择结构语法 1、什么是if-else语句? 2、if...else 循环基本用法 3、案例&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
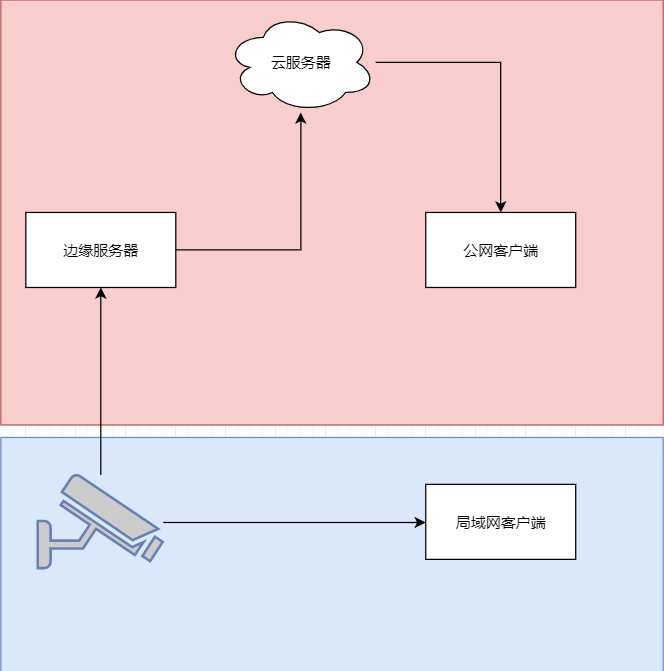
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...
