第四十四章 管理镜像 - 传入日记传输率
文章目录
- 第四十四章 管理镜像 - 传入日记传输率
- 传入日记传输率
- 镜像数据库状态
第四十四章 管理镜像 - 传入日记传输率
传入日记传输率
在备份和异步成员的镜像成员状态列表下方,自上次刷新镜像监视器以来日志数据从主服务器到达的速率显示在该成员的传入日志传输率下。
首次加载镜像监控页面时,该区域显示文本—(将在刷新时显示)。下次刷新页面时,显示的信息取决于传入的日志数据是否压缩(参见镜像流量压缩),如下:
- 如果日志数据未压缩,则传入日志数据速率以每秒千字节 (
KB) 为单位提供,例如:
42345 KB/s (22s interval)
- 如果传入的日志数据是压缩的,则显示包括传入的压缩数据速率、传入的日志(未压缩)数据速率以及后者与前者的比率,例如:
14288 KB/s network; 39687 KB/s journal; ratio 2.78:1 (143s interval)
镜像数据库状态
重要提示:在备份和 DR 异步成员上,镜像监视器页面上的丢失镜像数据库报告会提醒存在于主成员上但不存在于当前成员上的任何镜像数据库。这一点非常重要,因为备份或 DR 异步(如果提升为备份)如果没有完整的镜像数据库集,则无法在主中断的情况下成功接管。列出了每个缺失数据库的完整镜像数据库名称。如果没有缺失数据库,则不会显示缺失镜像数据库报告。
在所有成员上,“镜像监视器”页面上的“镜像数据库”列表显示列出的每个数据库的以下状态之一:
| Status | Description |
|---|---|
Normal (primary only) | 镜像数据库是可写的(如果不是只读数据库)并且正在记录全局更新。 |
Dejournaling (backup and async) | 数据库已被激活并赶上,镜像正在将日志数据应用到数据库。 |
Needs Catchup | 数据库已激活但尚未赶上;需要用户启动的 Catchup 操作。 |
Needs Activation | 数据库尚未激活;需要用户启动的 Activate 和 Catchup 操作。 |
Catchup Running | 用户启动的Catchup 操作正在数据库上运行。 |
| `Dejournaling Stopped | Dejournaling` 已被操作员或错误停止;请参阅停止对备份和异步成员的镜像和管理数据库取消日志记录。 |
Database Dismounted | 数据库已卸载。 |
Orphaned (backup and async) | 镜像数据库在主数据库上不存在。 |
Obsolete | 镜像数据库已过时,应从镜像中删除。 |
在主数据库上,如果数据库的状态为正常,则 Next Record to Dejournal 列包含 N/A。否则,该列包括以下内容:
Time是应用于数据库的下一条日志记录开始处的时间戳,如果它与主日志的当前位置匹配,则为Current。FileName是包含要应用的下一个日志记录的镜像日志文件的名称。- 偏移量是要应用的下一个日志记录的开头在日志文件中的位置。
数据库的状态和与其相关的操作(激活和同步)在激活和同步镜像数据库中讨论;这些操作在列表下方的下拉列表中可用。还可以使用下拉菜单来装载已卸载的数据库(但不能卸载已装载的数据库)。可以使用删除链接或从下拉列表中选择删除以从镜像中删除列出的数据库;
相关文章:

第四十四章 管理镜像 - 传入日记传输率
文章目录 第四十四章 管理镜像 - 传入日记传输率传入日记传输率镜像数据库状态 第四十四章 管理镜像 - 传入日记传输率 传入日记传输率 在备份和异步成员的镜像成员状态列表下方,自上次刷新镜像监视器以来日志数据从主服务器到达的速率显示在该成员的传入日志传输…...
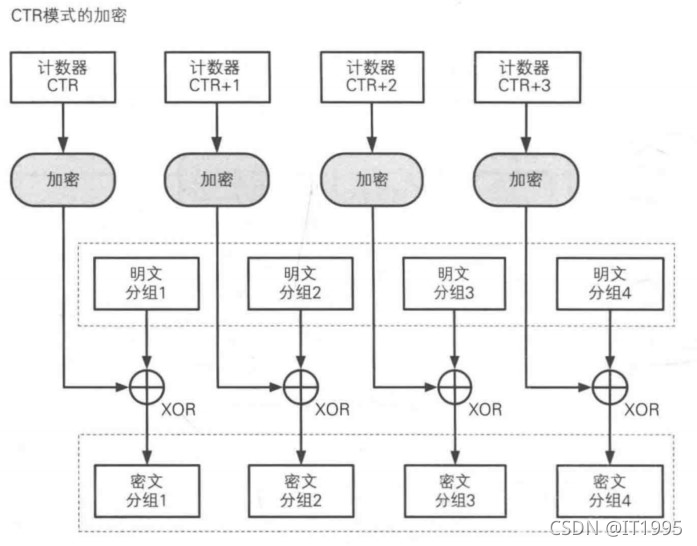
加密解密学习笔记
加密种类 对称加密,分组对称加密算法 加密算法 AES(Advanced Encryption Standard)高级加密标准 DES(Data Encryption Standard)数据加密标准 3DES/Triple DEA (Triple Data Encryption Algorithm) 三重数据加密算…...
)
Spring 属性填充源码分析(简单实用版)
属性填充 属性填充只有 3 种方式 根据名称填充 根据类型填充 思考什么时候会出现呢??? 多见于第三方框架与 Spring集成,举例:Mybatis 与 Spring集成,把 Mapper 接口注册为 BeanDefinition 时候就指定了自…...

【机器学习分支】重要性采样(Importance sampling)学习笔记
重要性采样(importance sampling)是一种用于估计概率密度函数期望值的常用蒙特卡罗积分方法。其基本思想是利用一个已知的概率密度函数来生成样本,从而近似计算另一个概率密度函数的期望值。 想从复杂概率分布中采样的一个主要原因是能够使用…...

三角回文数+123
三角回文数:用户登录 问题描述 对于正整数 n, 如果存在正整数 k 使得 n123⋯kk(k1)/2, 则 n 称为三角数。例如, 66066 是一个三角数, 因为 66066123⋯363 。 如果一个整数从左到右读出所有数位上的数字, 与从右到左读出所有数位 上的数字是一样的, 则称这个数为…...

JAVA常用的异步处理方法总结
前言 在java项目开发过程中经常会遇到比较耗时的任务,通常是将这些任务做成异步操作,在java中实现异步操作有很多方法,本文主要总结一些常用的处理方法。为了简化,我们就拿一个实际的案例,再用每种方法去实现…...

GitLab统计代码量
gitlab官方文档:https://docs.gitlab.com/ee/api/index.html 1、生成密钥 登录gitlab,编辑个人资料,设置访问令牌 2、获取当前用户所有可见的项目 接口地址 GET请求 http://gitlab访问地址/api/v4/projects?private_tokenxxx 返回参数 …...

Linux TCP MIB统计汇总
概述 在 linux > 4.7 才将所有TCP丢包收敛到 函数 tcp_drop 中 指标详解 cat /proc/net/netstat 格式化命令 cat /proc/net/netstat | awk (f0) {name$1; i2; while ( i<NF) {n[i] $i; i }; f1; next} (f1){ i2; while ( i<NF){ printf "%s%s %d\n", …...

记录 docker linux部署jar
第一步 web sso user admin 中yml文件还原到阿里mysql数据库 第二步 各个jar进行打包处理 第三步 正式服务器的Jar备份 第四步 拉取以上jar包 到正式服务器中 第五步 查看 docker images 其中 web_service 1.0.2是上一个版本 上一个版本build 镜像命令是这样的(需…...

【Linux】教你用进程替换制作一个简单的Shell解释器
本章的代码可以访问这里获取。 由于程序代码是一体的,本章在分开讲解各部分的实现时,代码可能有些跳跃,建议在讲解各部分实现后看一下源代码方便理解程序。 制作一个简单的Shell解释器 一、观察Shell的运行状态二、简单的Shell解释器制作原理…...

onMeasure里如何重置只有1个子view一行满屏, 若有多个自适应一行
onMeasure里如何重置只有1个子view一行满屏, 若有多个自适应一行 可以尝试在 onMeasure 方法中重写 measureChildWithMargins 或 measureChild 方法来实现这个需求。 对于只有一个字的 View,我们可以把它的宽度设为屏幕宽度,高度设为最大高度,这样这个 View 就会占满一整行…...
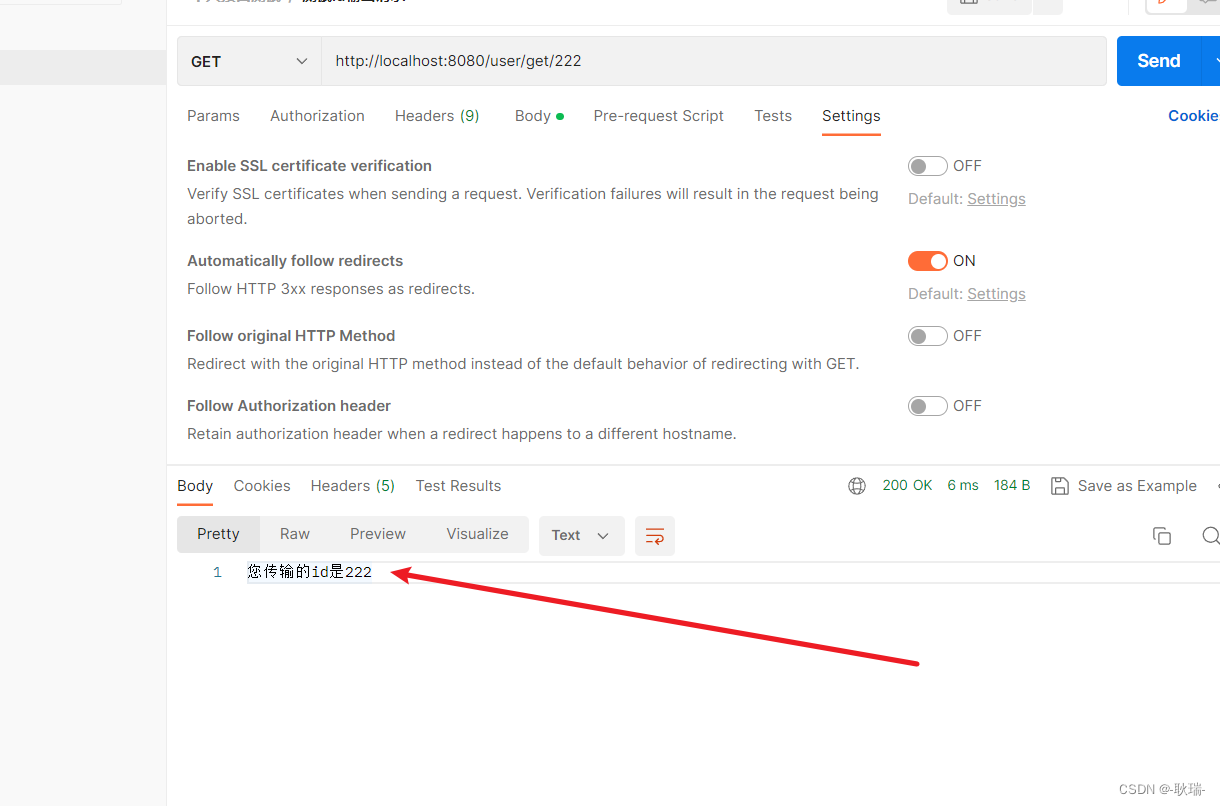
Postman创建项目 对接口发起请求处理
查看本文之前 您需要理解了解 Postman 的几个简单工作区 如果还没有掌握 可以先查看我的文章 简单认识 Postman界面操作 那么 掌握之后 我们就可以正式来开启我们的接口测试 我们先选择 Collections 我们点上面这个加号 多拉一个项目出来 然后 我们选我们刚加号点出来的项目…...

在Vue3项目中js-cookie库的使用
文章目录 前言1.安装js-cookie库2.引入、使用js-cookie库 前言 今天分享一下在Vue3项目中引入使用js-cookie。 1.安装js-cookie库 js-cookie官网 安装js-cookie,输入 npm i js-cookie安装完成可以在package.json中看到: 安装以后,就可…...

【论文笔记】Attention和Visual Transformer
Attention和Visual Transformer Attention和Transformer为什么需要AttentionAttention机制Multi-head AttentionSelf Multi-head Attention,SMA TransformerVisual Transformer,ViT Attention和Transformer Attention机制在相当早的时间就已经被提出了&…...

独立IP服务器和共享IP服务器有什么区别
在选择一个合适的服务器时,最常见的选择是共享IP服务器和独立IP服务器。尽管两者看起来很相似,但它们有着很大的不同。本文将详细介绍共享IP服务器和独立IP服务器的不同之处,以及如何选择适合您需求的服务器。 一、什么是共享IP服务器? 共享…...

Java8
Java8 (一)、双列集合(二)、Map集合常用api(三)、Map集合的遍历方式(四)、HashMap(五)、LinkedHashMap(六)、TreeMap(七&a…...

nn.conv1d的输入问题
Conv1d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue) in_channels(int) – 输入信号的通道。在文本分类中,即为词向量的维度out_channels(int) – 卷积产生的通道。有多少个out_channels,就需要多少个1维…...
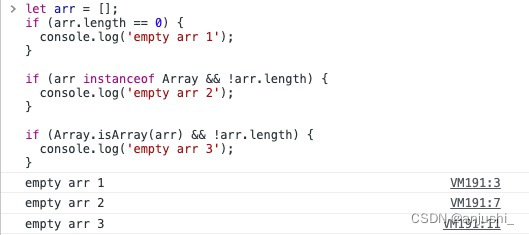
js判断是否为null,undefined,NaN,空串或者空对象
js判断是否为null,undefined,NaN,空串或者空对象 这里写目录标题 js判断是否为null,undefined,NaN,空串或者空对象特殊值nullundefinedNaN空字符串("")空对象(…...

Java每日一练(20230501)
目录 1. 路径交叉 🌟🌟 2. 环形链表 🌟🌟 3. 被围绕的区域 🌟🌟 🌟 每日一练刷题专栏 🌟 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专栏…...

从零开始学习Web自动化测试:如何使用Selenium和Python提高效率?
B站首推!2023最详细自动化测试合集,小白皆可掌握,让测试变得简单、快捷、可靠https://www.bilibili.com/video/BV1ua4y1V7Db 目录 引言: 一、了解Web自动化测试的基本概念 二、选择Web自动化测试工具 三、学习Web自动化测试的…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
