经典回归算法
回归的概念
回归方程:
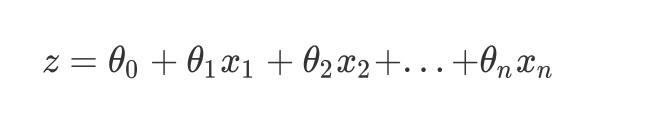
写成矩阵:
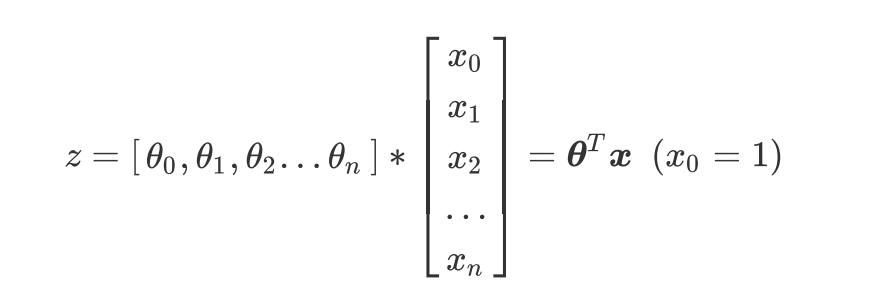
- 核心问题,构建预测函数z来映射特征矩阵x和标签y的线性关系
预测的目标值,有连续值也有离散值
- 连续值,就直接预测输出就行
- 离散值,需要在输出端加一个变换函数例如。Sigmoid函数,将连续值映射到【0,1】之间,即变成概率,根据概率大小就行判别分类
- Sigmoid函数也有致命的缺陷
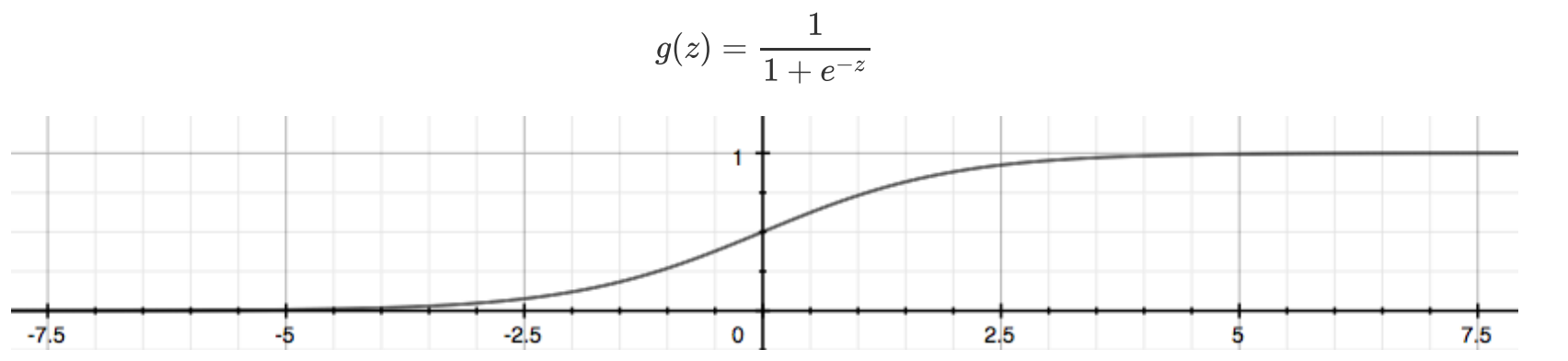
- Sigmoid函数也有致命的缺陷
- 正无穷趋近于1,负无穷趋近于0 ,会导致梯度爆炸和梯度消失
如何对标签值就行转换?
- 取对数,预测值y(x) 和 1 - y(x) 和必然为1,所以二者相除可以得到形似概率的结果

所以,叫作对数几率回归 logistic regression, 实质上在做分类
y(x)代表了样本为某一类标签的概率吗?
参考回答:

逻辑回归存在的问题
缺点:
线性回归对数据的要求很严格,比如标签必须满足正态分布,特征之间的多重共线性需要消除等等,而现实中很多
真实情景的数据无法满足这些要求,因此线性回归在很多现实情境的应用效果有限
- 逻辑回归由线性回归发展而来,当然存在这个问题
优点:
-
逻辑回归对线性关系的拟合效果好到丧心病狂。
- 特征与标签之间的线性关系极强的数据,比如金融领域中的信用卡欺诈,评分卡制作,电商中的营销预测等等相关的数据,都是逻辑回归的强项。
- 虽然现在有了梯度提升树GDBT,比逻辑回归效果更好,也被许多数据咨询公司启用,但逻辑回归在金融领域,尤其是银行业中的统治地位依然不可动摇
- 相对的,逻辑回归在非线性数据的效果很多时候比瞎猜还不如,所以如果你已经知道数据之间的联系是非线性的,千万不要迷信逻辑回归
-
逻辑回归计算快:对于线性数据,逻辑回归的拟合和计算都非常快,计算效率优于SVM和随机森林,亲测表
示在大型数据上尤其能够看得出区别 -
逻辑回归返回的分类结果不是固定的0,1,而是以小数形式呈现的类概率数字:我们因此可以把逻辑回归返
回的结果当成连续型数据来利用。- 比如在评分卡制作时,我们不仅需要判断客户是否会违约,还需要给出确定的”信用分“,而这个信用分的计算就需要使用类概率计算出的对数几率,而决策树和随机森林这样的分类器,可以产出分类结果,却无法帮助我们计算分数(当然,在sklearn中,决策树也可以产生概率,使用接口predict_proba调用就好,但一般来说,正常的决策树没有这个功能)。
详细理解

-
两种概率整合:yi的取值就是0或1 ,参数是cta
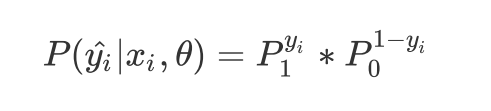
-
预测的概率P
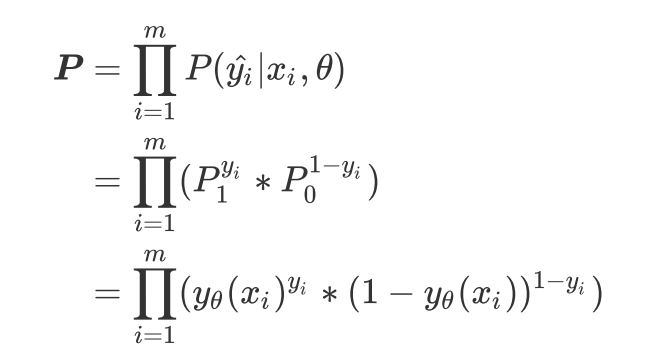
-
两边取对数
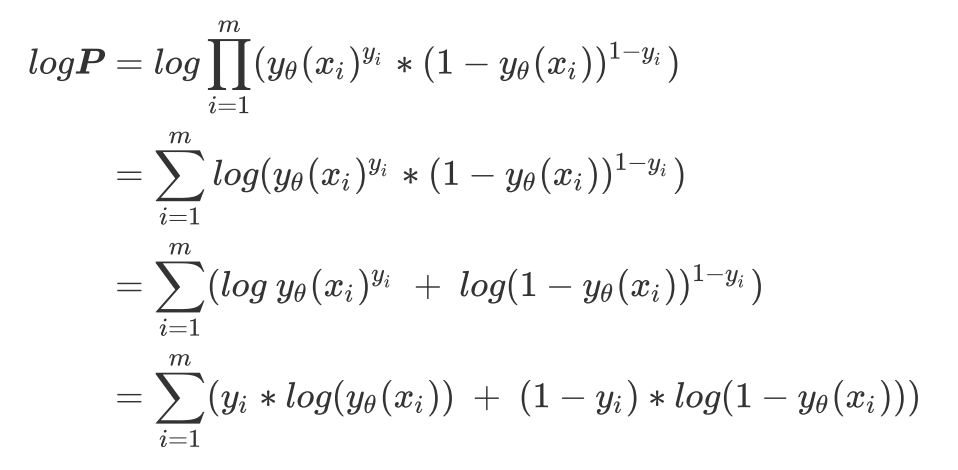
-
得到损失函数:用极大似然法推导
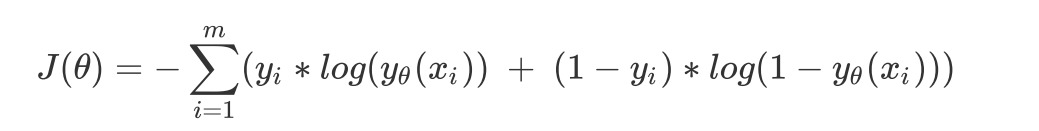
拟合:
逻辑回归和线性回归是天生欠拟合的模型,但我们还是需要控制过拟合的技术来帮助我们调整模型,对逻辑回归中过拟合的控制,通过正则化来实现。
正则化:
正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数向
量 θ \theta θ 的L1范式和L2范式的倍数来实现

L1正则化:
在L1正则化在逐渐加强的过程中,携带信息量小的、对模型贡献不大的特征的参数,会比携带大量信息的、对模型
有巨大贡献的特征的参数更快地变成0,所以L1正则化本质是一个特征选择的过程,掌管了参数的“稀疏性”。L1正
则化越强,参数向量中就越多的参数为0,参数就越稀疏,选出来的特征就越少
L2正则化:
L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大
的特征的参数会非常接近于0。通常来说,如果我们的主要目的只是为了防止过拟合,选择L2正则化就足够了。
逻辑回归中的特征工程
-
业务指标选择
- 直接凭借经验,选择通常相关性比较高的指标
-
PCA和SVD一般不用
- 说到降维,我们首先想到的是之前提过的高效降维算法,PCA和SVD,遗憾的是,这两种方法大多数时候不适用于
逻辑回归。逻辑回归是由线性回归演变而来,线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的
关系,而逻辑回归也传承了这个性质,我们常常希望通过逻辑回归的结果,来判断什么样的特征与分类结果相关,
因此我们希望保留特征的原貌。PCA和SVD的降维结果是不可解释的,因此一旦降维后,我们就无法解释特征和标
签之间的关系了。 - 当然,在不需要探究特征与标签之间关系的线性数据上,降维算法PCA和SVD也是可以使用的。
- 说到降维,我们首先想到的是之前提过的高效降维算法,PCA和SVD,遗憾的是,这两种方法大多数时候不适用于
-
统计方法可以使用,但不是非常必要
- 既然降维算法不能使用,我们要用的就是特征选择方法。逻辑回归对数据的要求低于线性回归,由于我们不是使用
最小二乘法来求解,所以逻辑回归对数据的总体分布和方差没有要求,也不需要排除特征之间的共线性- 解释一下特征共线性的问题:
- 在一些博客中有这样的观点:多重共线性会影响线性模型的效果。对于线性回归来说,多重共线性会影响比较大,
所以我们需要使用方差过滤和方差膨胀因子VIF(variance inflation factor)来消除共线性。但是对于逻辑回归,其实不是非常必要,甚至有时候,我们还需要多一些相互关联的特征来增强模型的表现 - 消除共线性的方法 : VIF , Box-cox方法
- 统计方法,比如方差,卡方,互信息等方法来做特征选择,也并没有问题。过滤法中所有的方法,都可以用在逻辑回归上
- 既然降维算法不能使用,我们要用的就是特征选择方法。逻辑回归对数据的要求低于线性回归,由于我们不是使用
处理:
- 直接embedding
- 方差贡献率,在逻辑回归中可以使用系数coef_来这样做
关于梯度下降的误区
对损失函数求最小值,自然而然就知道求导数,偏导数
- 注意 ∇ f ( x , y ) ∂ x \frac{\nabla f(x,y)}{\partial x} ∂x∇f(x,y), ∇ f ( x , y ) ∂ y \frac{\nabla f(x,y)}{\partial y} ∂y∇f(x,y) 其实 是对 θ \theta θ求导,然后链式求导法则来的,不是直接对x和y求偏导,得到梯度的
目标函数: J ( θ 1 , θ 2 , . . . ) , θ i ∈ θ 目标函数:J(\theta_1,\theta_2,...) ,\theta_i \in \theta 目标函数:J(θ1,θ2,...),θi∈θ
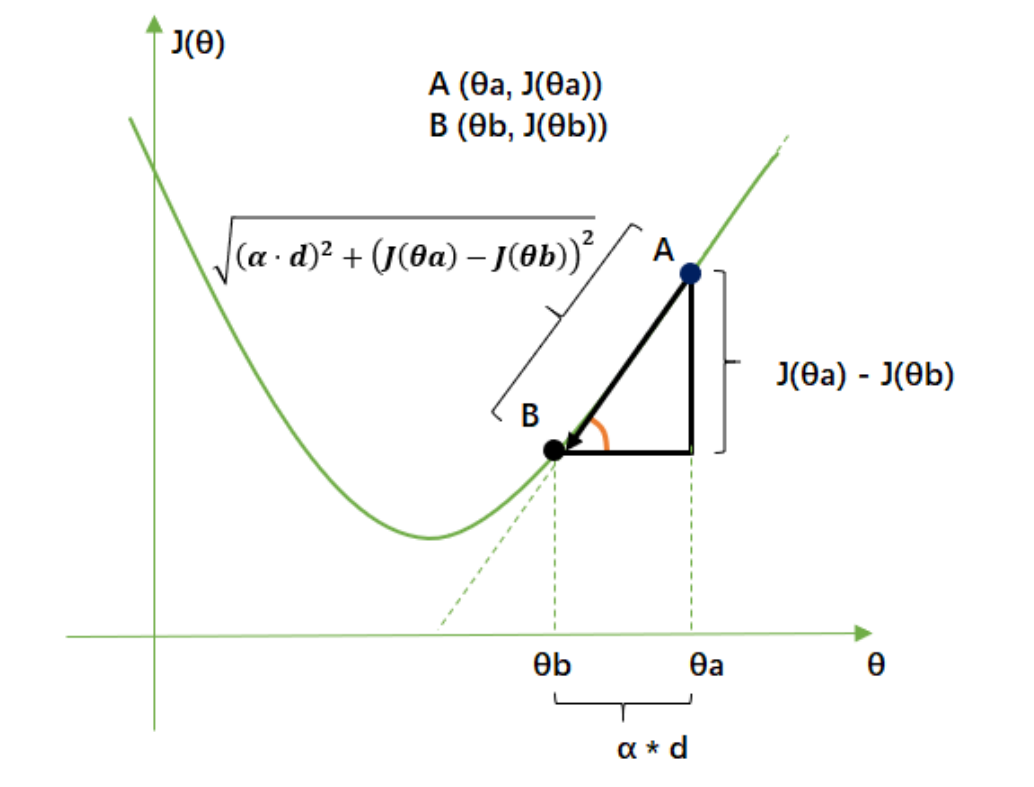
- 所以,步长不是任何物理距离,它甚至不是梯度下降过程中任何距离的直接变化,它是梯度向量的大小 d上的一个
比例,影响着参数向量 θ \theta θ 每次迭代后改变的部分。
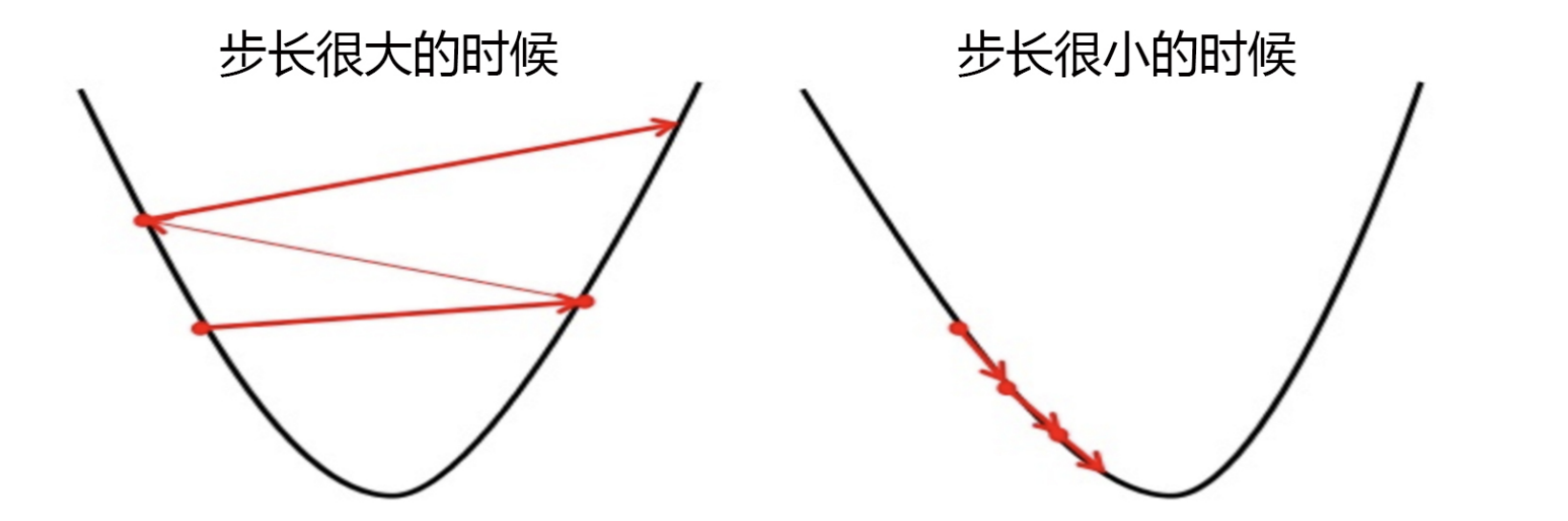
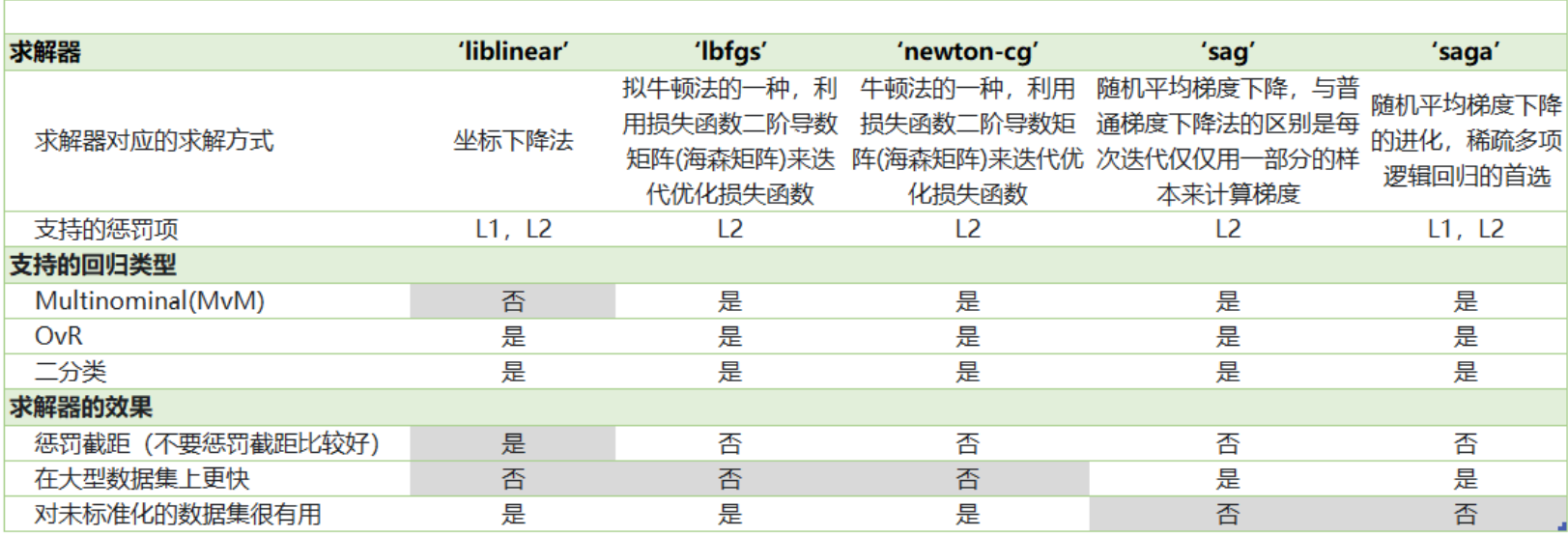
求解器
参数solver & multi_class : 二元回归与多元回归
- 样本不平衡与参数class_weight : 暂定是玄学
相关文章:

经典回归算法
回归的概念 回归方程: 写成矩阵: 核心问题,构建预测函数z来映射特征矩阵x和标签y的线性关系 预测的目标值,有连续值也有离散值 连续值,就直接预测输出就行离散值,需要在输出端加一个变换函数例如。Si…...

Python两三行代码轻松批量添加~防韩还是很有必要的~
人生苦短,我用python 一直想做一个这种系列的但是因为七七八八的事情总是忘记, 今天正好有空,来开整一下~ 首先, 天冷防韩是什么梗? 【天冷防韩】 “天冷防韩”是“天冷防寒”的谐音, 不过“寒”指的…...

开心消消乐
给定一个 N 行 M 列的二维矩阵,矩阵中每个位置的数字取值为 0 或 1,矩阵示例如: 1 1 0 0 0 0 0 1 0 0 1 1 1 1 1 1 现需要将矩阵中所有的 1 进行反转为 0,规则如下: 当点击一个 1 时,该 1 被反转为 0&am…...
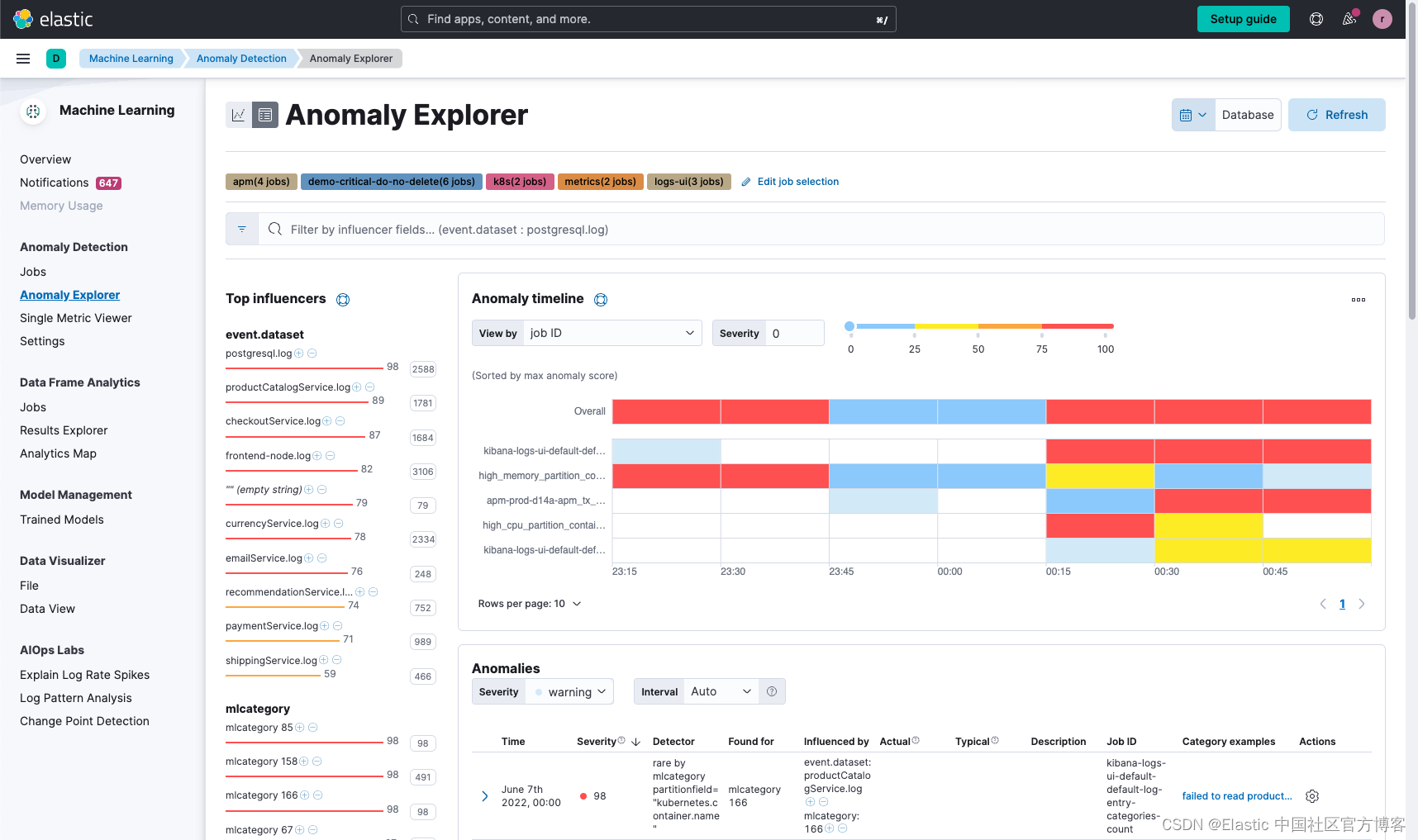
有效日志管理在软件开发和运营中的作用
作者:Luca Wintergerst, David Hope, Bahubali Shetti 当今存在的快速软件开发过程需要扩展和复杂的基础架构和应用程序组件,并且操作和开发团队的工作不断增长且涉及多个方面。 有助于管理和分析遥测数据的可观察性是确保应用程序和基础架构的性能和可靠…...
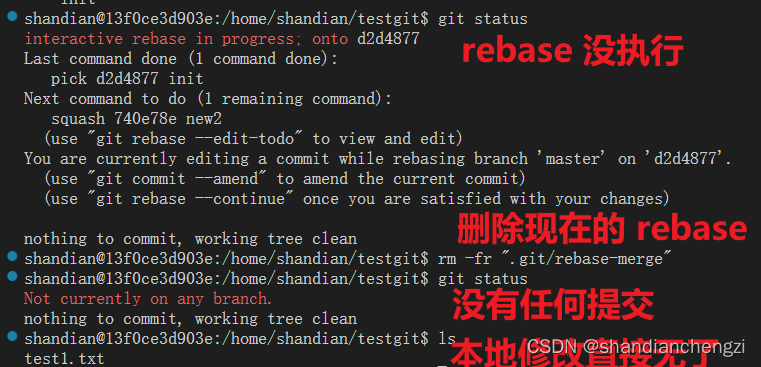
【五一创作】【笔记】Git|如何将仓库中所有的 commit 合成一个?又名,如何清除所有 git 提交记录?(附 git rebase 机制的简要分析)
在对代码进行开源时,我们往往并不希望代码开发过程中的提交记录被其他人看到,因为提交的过程中往往会涵盖一些敏感信息。因此会存在 将仓库中所有 commit 合成一个 的需求。 直觉上,往往会用 rebase 和 squash 或 reset,不过我尝…...

如何写出高质量代码?
作为一名资深开发人员,写出高质量的代码是我们必须要追求的目标。然而,在实际开发中,我们常常会遇到各种问题。比如,代码的可读性、可维护性、健壮性和灵活性等,这些都会影响代码的质量。那么,究竟如何才能…...

外卖项目优化-01-redis缓存短信验证码、菜品数据、Spring Cache(注解开发缓存)、(注解开发)缓存套餐数据
文章目录 外卖项目优化-01课程内容前言1. 环境搭建1.1 版本控制解决branch和tag命名冲突 1.2 环境准备 2. 缓存短信验证码2.1 思路分析2.2 代码改造2.3 功能测试 3. 缓存菜品信息3.1 实现思路3.2 代码改造3.2.1 查询菜品缓存3.2.2 清理菜品缓存 3.3 功能测试3.4 提交并推送代码…...
)
Chapter1:控制系统数学模型(下)
第一章:控制系统数学模型 Exercise1.13 已知控制系统结构图如下图所示,求系统的输出 C 1 ( s ) C_1(s) C...
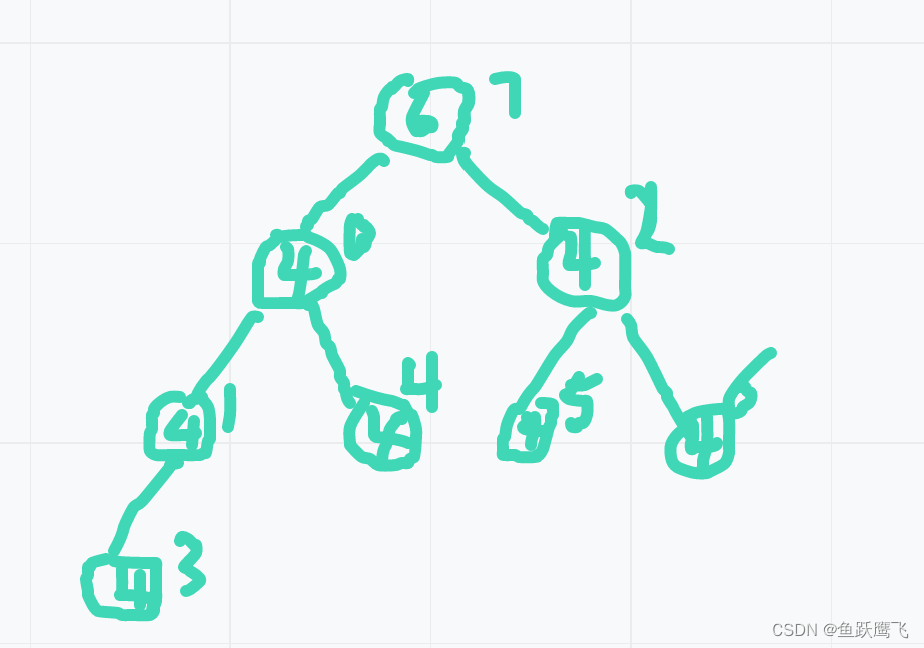
排序算法总结
常见排序算法的时间复杂度、空间复杂度及稳定性分析: 时间复杂度空间复杂度是否有稳定性基于比较的排序算法选择排序 O(N^2)O(1)否 冒泡排序O(N^2)O(1)是插入排序O(N^2)O(1)是归并排序O(N*logN)O(N),每次需要额外一个数组用于拷贝是快排O(N*log…...
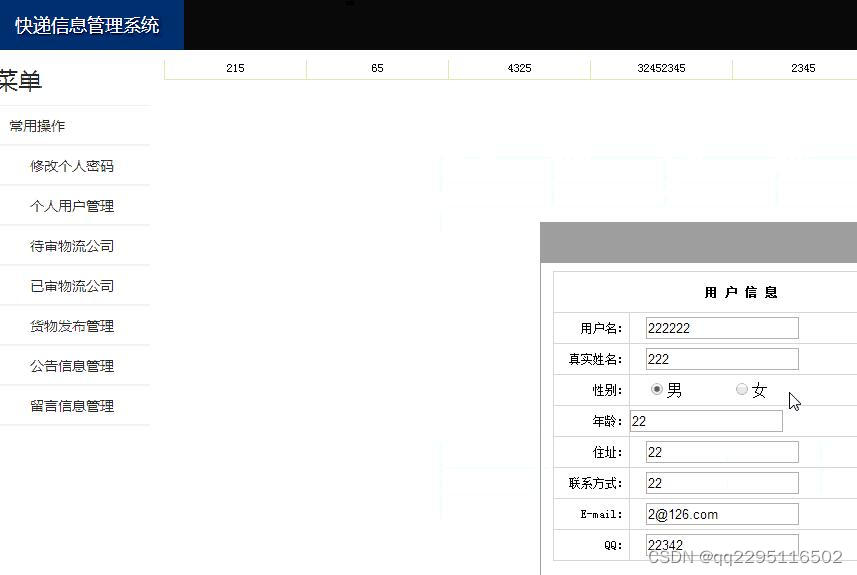
java+jsp企业物流货运快递管理系统servlet
功能需求具体描述: (1)用户功能模块包括用户登录注册,用户信息的修改,用户发布货物信息,给客服人员留言,对运输公司进行评价。 (2)企业功能模块包括企业注册登录,企业信息的修改,受理用户发布的…...

【ROS仿真实战】获取机器人在gazebo位置真值的三种方法(三)
文章目录 前言一. 使用ROS tf库二、 使用Gazebo Model Plugin三、 使用libgazebo_ros_p3d插件四、总结 前言 在ROS和Gazebo中,获取机器人的位置信息通常通过ROS消息传递进行。在这篇文章中,我们将介绍三种获取机器人在Gazebo中位置真值的方法࿱…...
——FontDialog(史上最全))
Winform从入门到精通(35)——FontDialog(史上最全)
文章目录 前言一、属性1、Name2、AllowScriptChange3、AllowSimulations4、AllowVectorFonts5、AllowVerticalFonts6、Color7、FixedPitchOnly8、Font9、FontMustExist10、MaxSize11、MinSize12、 ScriptsOnly13、ShowApply14、ShowColor15、ShowEffects16、ShowHelp...

AcWing 854. Floyd求最短路Floyd模板
Floyd算法: 标准弗洛伊德算法,三重循环,基于动态规划。 循环结束之后 d[i][j]存储的就是点 i 到点 j 的最短距离。 需要注意循环顺序不能变:第一层枚举中间点,第二层和第三层枚举起点和终点。 特点: 1.复杂…...
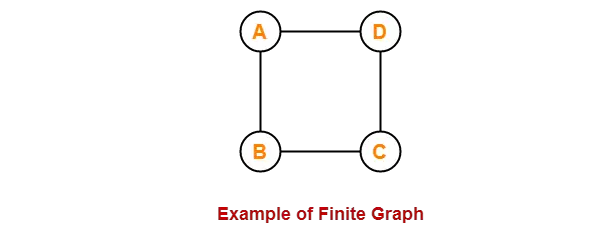
Graph Theory(图论)
一、图的定义 图是通过一组边相互连接的顶点的集合。 In this graph, V { A , B , C , D , E } E { AB , AC , BD , CD , DE } 二、图的类型 2.1 Finite Graph A graph consisting of finite number of vertices and edges is called as a finite graph. Null Graph Tri…...

[Python]生成 txt 文件
前段时间有位客户问: 你们的程序能不能给我们生成个 txt 文件,把新增的员工都放进来,字段也不需要太多,就要 员工姓名/卡号/员工编号/员工职位/公司 这些字段就行了,然后我们的程序会去读取这个 txt 文件,拿里面的内容,读完之后会这个文件删掉 我: 可以接受延迟吗?可能没办法实…...

GeoTools实战指南: 自定义矢量样式并生成截图
GeoTools实战指南: 自定义矢量样式并生成截图 介绍 本段代码的主要功能是将矢量数据(Shapefile)渲染成一张图片。 准备环境 首先,您需要将GeoTools库添加到您的项目中。使用Maven或Gradle添加依赖项,或者直接下载GeoTools的jar文件并添加到您的类路径中。 Maven <…...

深度学习超参数调整介绍
文章目录 深度学习超参数调整介绍1. 学习率2. 批大小3. 迭代次数4. 正则化5. 网络结构总结 深度学习超参数调整介绍 深度学习模型的性能很大程度上取决于超参数的选择。超参数是指在训练过程中需要手动设置的参数,例如学习率、批大小、迭代次数、网络结构等等。选择…...
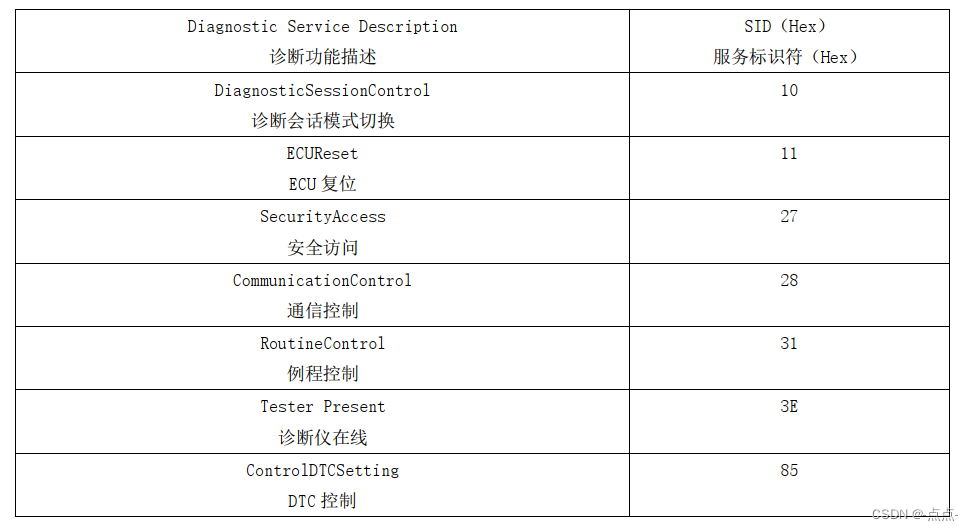
Bootloader
本篇不作太过的技术了解,仅可作为初学者的参考。用嘴简单的语言讲清楚一件事。 项目中遇到Bootloader升级MCU,我很好这是什么软件,逻辑是什么,怎么升级的。 术语及定义 指纹信息fingerprint诊断仪用于标识特定的下载尝试的信息 …...

安卓开发_广播机制_广播的最佳实践:实现强制下线功能
安卓开发_广播机制_广播的最佳实践:实现强制下线功能 ActivityCollector类用于管理所有的ActivityBaseActivity类作为所有Activity的父类创建一个LoginActivity来作为登录界面布局LoginActivity 在MainActivity中加入强制下线功能布局MainActivity在BaseActivity中注…...
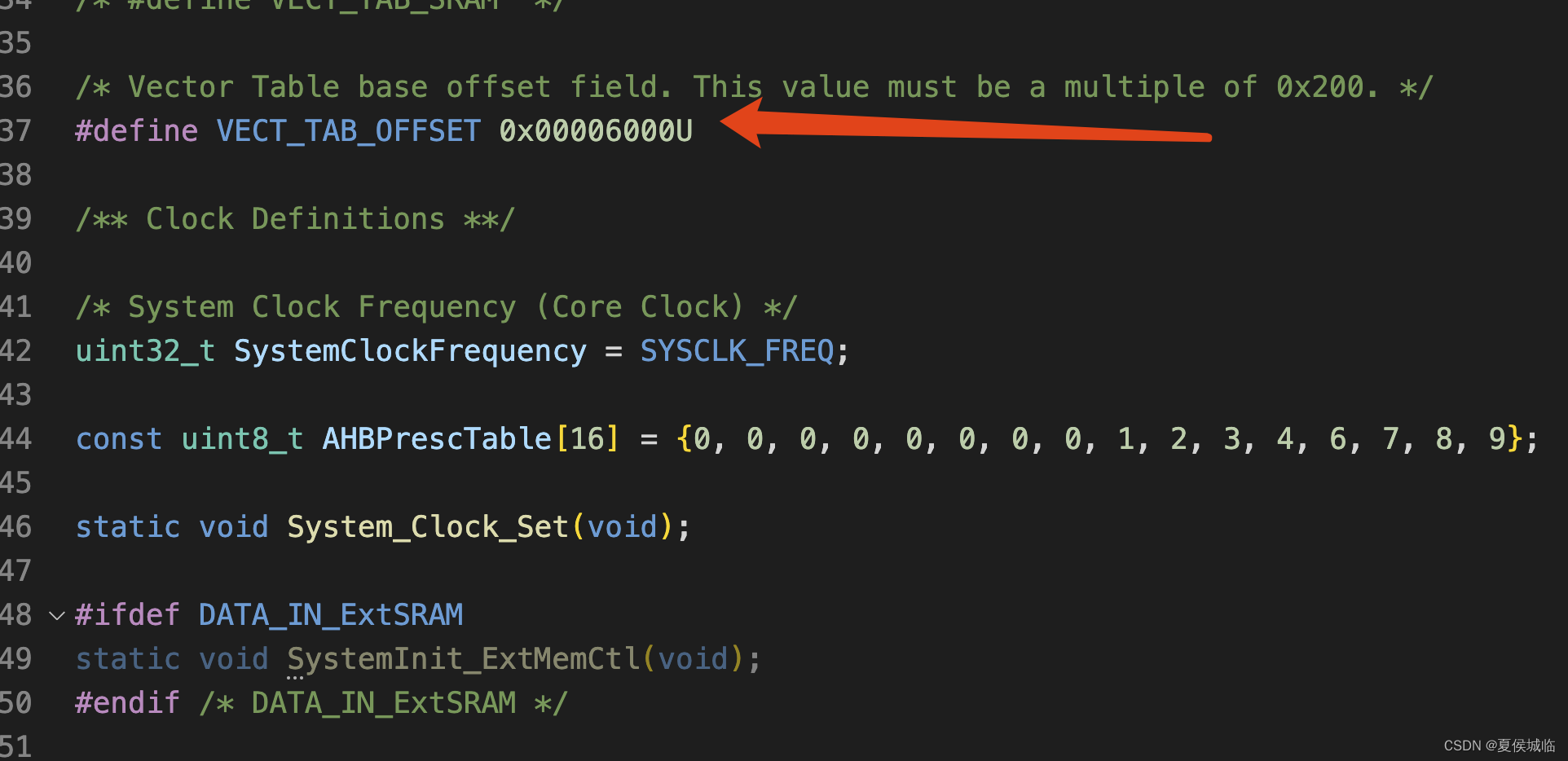
国民技术N32G430开发笔记(10)- IAP升级 Application 的制作
IAP升级 Application 的制作 1、App程序跟Bootloader程序最大的区别就是, 程序的执行地址变成了之前flash设定的0x08006000处, 大小限制为20KB 所以修改Application工程的ld文件 origin 改成 0x08006000 length 改成0x5000 烧录是起始地址也要改为x0x…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
