武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 + x 3 \int \frac{\rm dx}{1+x^3} ∫1+x3dx
解法一:
待定系数法:
∫ d x 1 + x 3 \int \frac{dx}{1+x^3} ∫1+x3dx
= ∫ d x ( 1 + x ) ( x 2 − x + 1 ) =\int \frac{dx}{(1+x)(x^2-x+1)} =∫(1+x)(x2−x+1)dx
= 1 3 ∫ ( 1 x + 1 + − x + 2 x 2 − x + 1 ) d x =\frac{1}{3} \int(\frac{1}{x+1} +\frac{-x+2}{x^2-x+1})\,{\rm d}x =31∫(x+11+x2−x+1−x+2)dx
= 1 3 [ ln ∣ x + 1 ∣ − 1 2 ∫ ( 2 x − 1 ) − 3 x 2 − x + 1 d x ] =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{2}\int\frac{(2x-1)-3}{x^2-x+1}\,{\rm d}x] =31[ln∣x+1∣−21∫x2−x+1(2x−1)−3dx]
= 1 3 [ ln ∣ x + 1 ∣ − 1 6 ∫ d ( x 2 − x + 1 ) x 2 − x + 1 + 1 2 ∫ 1 ( x − 1 2 ) 2 + 3 4 d x =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{6}\int\frac{d(x^2-x+1)}{x^2-x+1}+\frac{1}{2}\int\frac{1}{(x-\frac{1}{2})^2+\frac{3}{4}}\,{\rm d}x =31[ln∣x+1∣−61∫x2−x+1d(x2−x+1)+21∫(x−21)2+431dx
= 1 3 [ ln ∣ x + 1 ∣ − 1 6 ln ∣ x 2 − x + 1 ∣ + 1 2 × 1 3 2 arctan x − 1 2 3 2 + C =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{6}\ln\lvert x^2-x+1\rvert+\frac{1}{2}\times\frac{1}{\frac{\sqrt{3}}{2}}\arctan {\frac{x-\frac{1}{2}}{\frac{\sqrt{3}}{2}}}+C =31[ln∣x+1∣−61ln∣x2−x+1∣+21×231arctan23x−21+C
= 1 3 [ ln ∣ x + 1 ∣ − 1 6 ln ∣ x 2 − x + 1 ∣ + 1 3 arctan 2 x − 1 3 + C =\frac{1}{3}[\ln \lvert x+1\rvert-\frac{1}{6}\ln\lvert x^2-x+1\rvert+\frac{1}{\sqrt{3}}\arctan{\frac{2x-1}{\sqrt{3}}}+C =31[ln∣x+1∣−61ln∣x2−x+1∣+31arctan32x−1+C
草稿:
原式 = ∫ ( A x + 1 + B x + C x 2 − x + 1 ) d x 原式=\int( \frac{A}{x+1}+\frac{Bx+C}{x^2-x+1})\,{\rm d}x 原式=∫(x+1A+x2−x+1Bx+C)dx
则 A ( x 2 − x + 1 ) + ( B x + C ) ( x + 1 ) = 1 则A(x^2-x+1)+(Bx+C) (x+1)=1 则A(x2−x+1)+(Bx+C)(x+1)=1
即 A + B = 0 ; − A + B + C = 0 ; A + C = 1 即A+B=0;-A+B+C=0;A+C=1 即A+B=0;−A+B+C=0;A+C=1
解得 C = 2 3 , A = 1 3 , B = − 1 3 解得C=\frac{2}{3},A=\frac{1}{3},B= -\frac{1}{3} 解得C=32,A=31,B=−31
解法二:
灵活应用加项减项
可以看武忠祥老师每日一题||不定积分基础训练(三)
∫ 1 1 + x 3 d x \int \frac{1}{1+x^3}\,{\rm d}x ∫1+x31dx
= 1 2 ∫ ( 1 + x ) + ( 1 − x ) 1 + x 3 d x =\frac{1}{2}\int \frac{(1+x)+(1-x)}{1+x^3}\,{\rm d}x =21∫1+x3(1+x)+(1−x)dx
= 1 2 ∫ ( 1 + x ) + ( 1 − x ) ( 1 − x + x 2 ) ( 1 + x ) =\frac{1}{2}\int\frac{(1+x)+(1-x)}{(1-x+x^2)(1+x)} =21∫(1−x+x2)(1+x)(1+x)+(1−x)
= 1 2 [ 2 3 arctan 2 x − 1 3 + ln ∣ x + 1 ∣ − 1 3 ln ∣ x 3 + 1 ∣ ] + C =\frac{1}{2}[\frac{2}{\sqrt{3}}\arctan{\frac{2x-1}{\sqrt{3}}}+\ln\lvert x+1\rvert-\frac{1}{3}\ln \lvert x^3+1 \rvert]+C =21[32arctan32x−1+ln∣x+1∣−31ln∣x3+1∣]+C
类题拓展:
∫ x 1 + x 3 d x \int \frac{x}{1+x^3}\,{\rm d}x ∫1+x3xdx
= 1 2 ∫ ( 1 + x ) − ( 1 − x ) 1 + x 3 d x =\frac{1}{2}\int \frac{(1+x)-(1-x)}{1+x^3}\,{\rm d}x =21∫1+x3(1+x)−(1−x)dx
= 1 2 [ 2 3 arctan 2 x − 1 3 − ( ln ∣ x + 1 ∣ − 1 3 ln ∣ x 3 + 1 ∣ ) ] + C =\frac{1}{2}[\frac{2}{\sqrt{3}}\arctan{\frac{2x-1}{\sqrt{3}}}-(\ln\lvert x+1\rvert-\frac{1}{3}\ln \lvert x^3+1 \rvert)]+C =21[32arctan32x−1−(ln∣x+1∣−31ln∣x3+1∣)]+C
相关文章:
)
武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 x 3 \int \frac{\rm dx}{1x^3} ∫1x3dx 解法一: 待定系数法: ∫ d x 1 x 3 \int \frac{dx}{1x^3} ∫1x3dx ∫ d x ( 1 x ) ( x 2 − x 1 ) \int \frac{dx}{(1x)(x^2-x1)} ∫(1x)(x2−x1)dx 1 3 ∫ ( 1 x 1 − x 2 x 2 − x …...

记一次产线打印json导致的redis连接超时
服务在中午十一点上线后,服务每分钟发出三到四次redis连接超时告警。错误信息为: Dial err:dial tcp: lookup xxxxx: i/o timeout 排查过程 先是检查redis机器的情况,redis写入并发数较大,缓存中保留了一小时大概400w条数据。red…...

FPGA入门系列12--RAM的使用
文章简介 本系列文章主要针对FPGA初学者编写,包括FPGA的模块书写、基础语法、状态机、RAM、UART、SPI、VGA、以及功能验证等。将每一个知识点作为一个章节进行讲解,旨在更快速的提升初学者在FPGA开发方面的能力,每一个章节中都有针对性的代码…...

【三十天精通Vue 3】第二十六天 Vue3 与 TypeScript 最佳实践
✅创作者:陈书予 🎉个人主页:陈书予的个人主页 🍁陈书予的个人社区,欢迎你的加入: 陈书予的社区 🌟专栏地址: 三十天精通 Vue 3 文章目录 引言一、为什么使用TypeScript?二、Vue 3和TypeScript…...

ffmpeg-mov-metadate不识别Bug修复
文章目录 BUG起因类似问题反馈问题解决具体步骤: 阅读过文章ffmpeg命令行解析调试流程记录movenc.c源码分析 BUG起因 在ffmpeg参数默认可识别的metadata参数如下: 具体可见libavformat/movenc.c->mov_write_udta_tag() mov_write_string_metadata(s,…...
(8.6) 引导程序更新)
(8)(8.6) 引导程序更新
文章目录 前言 1 我在哪里可以下载最新的引导程序? 2 使用任务规划器进行升级...
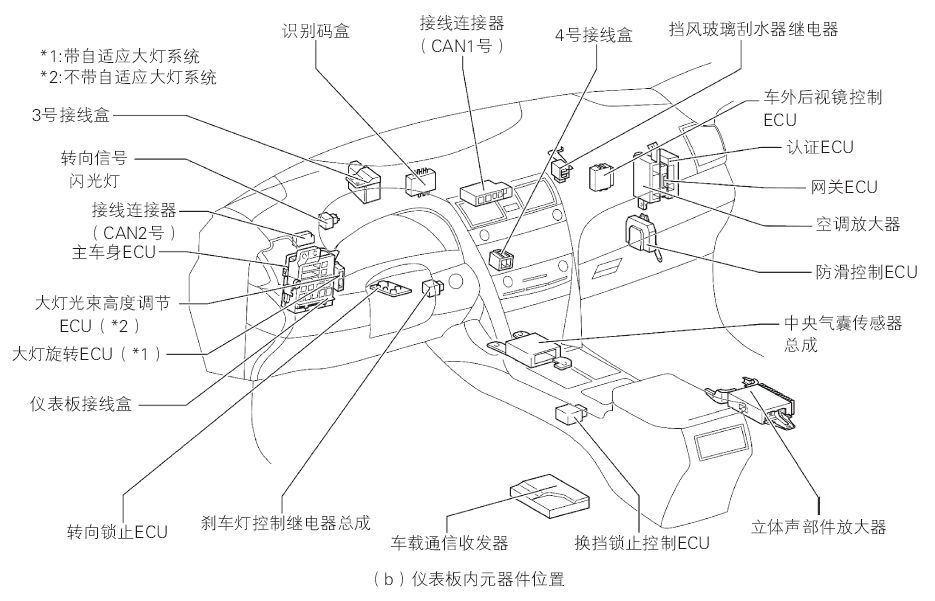
汽车电路图、原理框图、线束图、元器件布置图的识读技巧与要点
摘要: 想要读懂汽车电路图就必须把电的通路理清楚,即某条线是什么信号,该信号是输入信号、输出信号还是控制信号以及信号起什么作用,在什么条件下有信号,从哪里来,到哪里去。 一、汽车电路图的识读技巧 1.…...
( 数组和矩阵) 667. 优美的排列 II ——【Leetcode每日一题】
❓667. 优美的排列 II 难度:中等 给你两个整数 n 和 k ,请你构造一个答案列表 answer ,该列表应当包含从 1 到 n 的 n 个不同正整数,并同时满足下述条件: 假设该列表是 answer [a1, a2, a3, ... , an] ࿰…...

【python基础语法七】python内置函数和内置模块
内置全局函数 abs 绝对值函数 print(abs(-1)) # 1 print(abs(100)) # 100round 四舍五入 """奇进偶不进(n.5的情况特定发生)""" res round(3.87) # 4 res round(4.51) # 5 # res round(2.5) # 2 # res round(3.5) # 4 res round(6.5) # …...

81. read readline readlines 读取文件的三种方法
81. read readline readlines 读取文件的三种方法 文章目录 81. read readline readlines 读取文件的三种方法1. 读取文件的三种方法2. read方法3. readline方法4. readlines方法5. 代码总结5.1 read方法读取全部内容5.2 readline方法读取一行,返回字符串5.3 readli…...

【社区图书馆】【图书活动第四期】
目录 一、前言 二、作者简介 三、《PyTorch高级机器学习实战》内容简介 四、书目录 一、前言 今天,偶尔逛到csdn社区图书馆,看到有活动 “【图书活动第四期】来一起写书评领实体奖牌红包电子勋章吧!”(活动到今天结束…...
)
webpack学习指南(上)
构建流程 Webpack 的构建流程可以分为以下几个步骤: 解析配置文件:Webpack 会读取项目中的 webpack.config.js 文件,并解析其中的配置项。 解析入口文件:Webpack 通过配置文件中设置的 entry 入口,递归地解析出所有依…...
刷题记录˃ʍ˂
一、1033. 移动石子直到连续 思路 这道题是一道数学题,它一共分为三种可能 第一种可能为三个石子本来就是连续的时候 第二种可能为最少步数为1的时候,相邻石子不能大于一格 第三种可能为最少步数为2的时候,这时相邻石子大于一格 那么第二…...
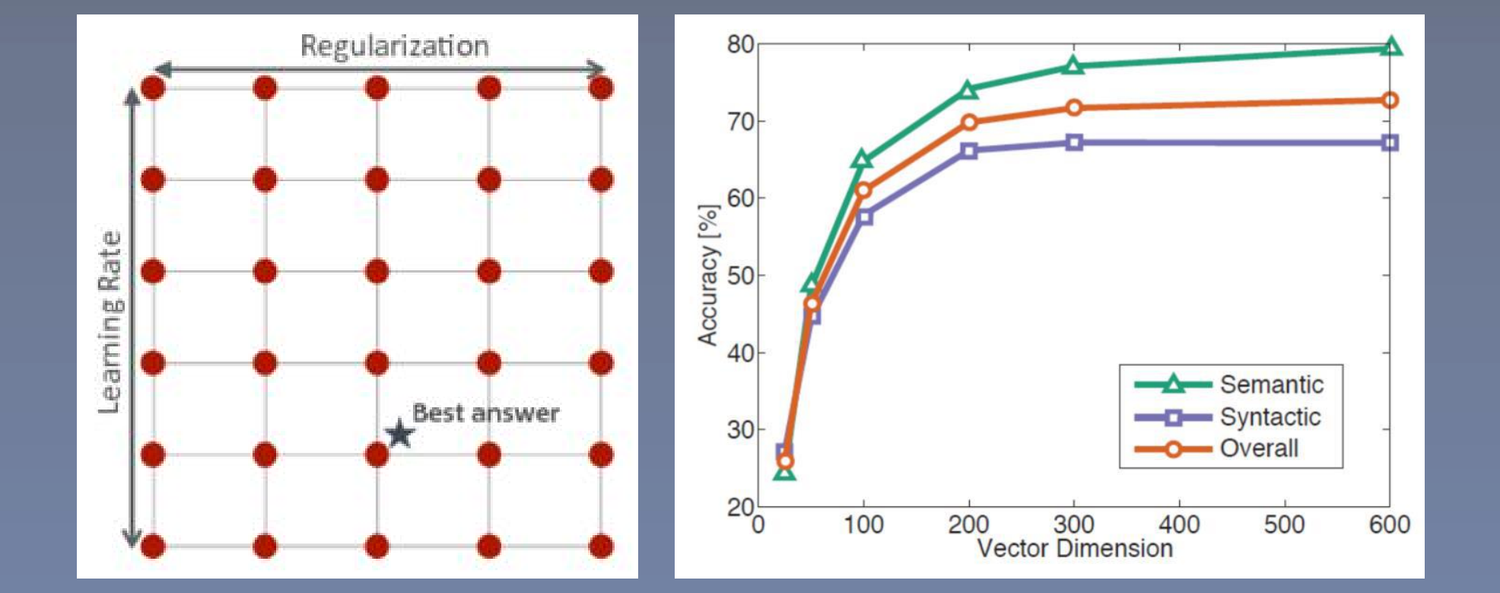
Word2vec原理+实战学习笔记(二)
来源:投稿 作者:阿克西 编辑:学姐 前篇:Word2vec原理实战学习笔记(一) 视频链接:https://ai.deepshare.net/detail/p_5ee62f90022ee_zFpnlHXA/6 5 对比模型(论文Model Architectur…...

什么是Java的多线程?
Java的多线程是指在同一时间内,一个程序中同时运行多个线程。每个线程都是一个独立的执行路径,可以独立地执行代码。Java中的多线程机制使得程序可以更高效地利用计算机的多核处理器和CPU时间,从而提高程序的性能和响应能力。 创建和使用Jav…...

“use strict“是什么? 使用它有什么优缺点?
严格模式 - JavaScript | MDN Javascript 严格模式详解 - 阮一峰的网络日志 1、"use strict" 是什么? "use strict" :指定代码在严格条件下执行; 2、 使用 "use strict" 有什么优缺点? ① 严格模式通过抛出错…...
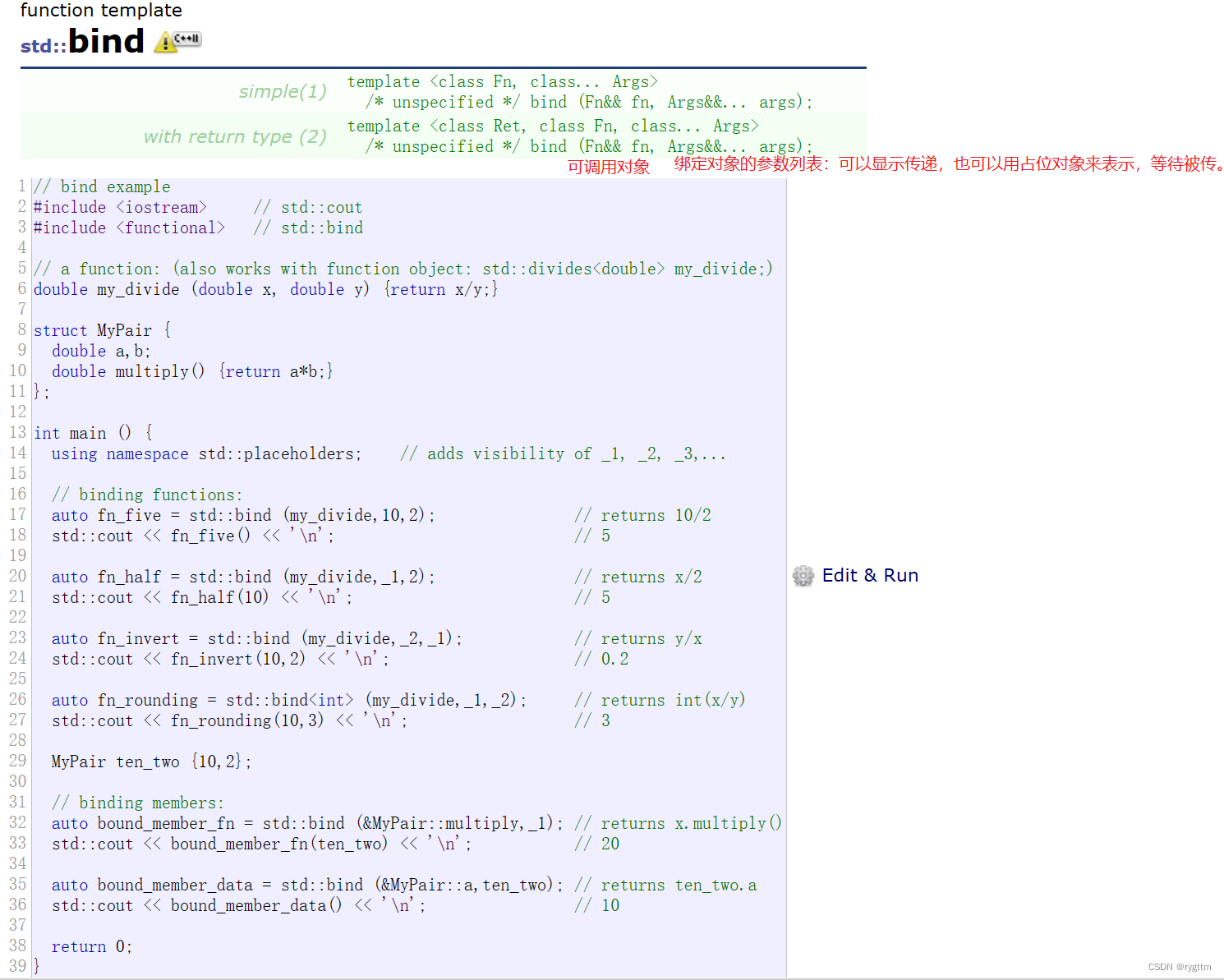
【C++】C++11常用特性总结
哥们哥们,把书读烂,困在爱里是笨蛋! 文章目录 一、统一的列表初始化1.统一的{}初始化2.std::initializer_list类型的初始化 二、简化声明的关键字1.decltype2.auto && nullptr 三、STL中的一些变化1.新增容器:array &…...

泛型——List 优于数组
数组与泛型有很大的不同: 1. 数组是协变的(covariant) 意思是:如果Sub是Super的子类型,则数组类型Sub[] 是数组类型Super[] 的子类型。 2. 泛型是不变的(invariant) 对于任何两种不同的类型Ty…...

JavaScript中对象的定义、引用和复制
JavaScript是一种广泛使用的脚本语言,其设计理念是面向对象的范式。在JavaScript中,对象就是一系列属性的集合,每个属性包含一个名称和一个值。属性的值可以是基本数据类型、对象类型或函数类型,这些类型的值相互之间有着不同的特…...

JavaScript通过函数异常处理来输入圆的半径,输出圆的面积的代码
以下为实现通过函数异常处理来输入圆的半径,输出圆的面积的代码和运行截图 目录 前言 一、通过函数异常处理来输入圆的半径,输出圆的面积 1.1 运行流程及思想 1.2 代码段 1.3 JavaScript语句代码 1.4 运行截图 前言 1.若有选择,您可以…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
