手把手教你搭建ROS阿克曼转向小车之(增量式PID代码实现)
在上一篇文章中我们已经成功的把编码器的反馈值给计算出来,这篇文章将会讲解怎么使用反馈回来的速度值进行PID计算,从而闭环控制电机的速度。
PID算法介绍
1.开环控制系统
开环控制系统(open-loop control system)是指被控对象的输出(被控制量)对控制器(controller)的输出没有影响。在这种控制系统中,不依赖将被控量反送回来以形成任何闭环回路。
2.闭环控制系统
闭环控制系统(closed-loop control system)的特点是系统被控对象的输出(被控制量)会反送回来影响控制器的输出,形成一个或多个闭环。闭环控制系统有正反馈和负反馈,若反馈信号与系统给定值信号相反,则称为负反馈( NegativeFeedback),若极性相同,则称为正反馈,一般闭环控制系统均采用负反馈,又称负反馈控制系统。闭环控制系统的例子很多。比如人就是一个具有负反馈的闭环控制系统,眼睛便是传感器,充当反馈,人体系统能通过不断的修正最后作出各种正确的动作。如果没有眼睛,就没有了反馈回路,也就成了一个开环控制系统。另例,当一台真正的全自动洗衣机具有能连续检查衣物是否洗净,并在洗净之后
能自动切断电源,它就是一个闭环控制系统。
3.阶跃响应
阶跃响应是指将一个阶跃输入(step function)加到系统上时,系统的输出。稳态误差是指系统的响应进入稳态后﹐系统的期望输出与实际输出之差。控制系统的性能可以用稳、准、快三个字来描述。稳是指系统的稳定性(stability),一个系统要能正常工作,首先必须是稳定的,从阶跃响应上看应该是收敛的﹔准是指控制系统的准确性、控制精度,通常用稳态误差来(Steady-state error)描述,它表示系统输出稳态值与期望值之差﹔快是指控制系统响应的快速性,通常用上升时
间来定量描述。
4.PID控制的原理和特点
将偏差的比例(Proportion)、积分(Integral)和微分(Differential)通过线性组合构成控制量,用这一控制量对被控对象进行控制,这样的控制器称 PID 控制器。
PID 控制器问世至今已有近 70 年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用 PID 控制技术最为方便。即当我们不完全了解一个系统和被控对象﹐ 或不能通过有效的测量手段来获得系统参数时,最适合用 PID 控制技术。 PID 控制,实际中也有 PI 和 PD控制。 PID 控制器就是根据系统的误差,利用比例、积分、微分计算出控制量进行控制的。
以电机转速控制为例。 之前的直流减速电机章节已经介绍了调节 PWM 占空比可以实现电机调试,编码器可以检测当前电机转速。那现在我需要控制电机转速为 3 圈/s(目标速度), 并且是不同负载下都控制在这个速度。开始电机处于停止状态此时PWM占空比为0, 然后我们改变占空比为45%,电机旋转,通过编码器我们得到当前的速度只有 2.5 圈/s,此时我们需要加大占空比,给到 50%, 编码器得到速度才 2.8 圈/s; 没办法, 我们还需要再加占空比,改为 55%,编码器得到 3.1 圈/s,惨了给大了,再调, 改为 54%, 这次幸运了,编码器速度再 3 圈/s 左右变动,勉强满足要求。
如果现在为电机加了一些负载,本来占空比 54%有 3 圈/s 的速度的,现在下降为 2.3 圈/s 了,现在为达到 3 圈/s 速度,又要类似上面的尝试修改过程,改为60%, 只有 2.5 圈/s,改为 80%, 超了,到了 3.2 圈/s, 改为 77%,差一点点,改为 78%, 效果还不错。
上面的占空比修改过程,是通过我们人为根据编码器反馈回来的数据数据经过我们大脑处理后优化出来的调整过程。如果我现在想要编程实现这个自动调整过程:就是不管增加负载还是减少负载, 都让程序自己调整占空比使得电机转速控制在 3 圈/s, 程序自动调整占空比过程,不外乎当速度小了就加大占空比,速度大了就减少占空比,主要是问题是究竟大多少或者减多少,我们大脑的一般想法就是当前速度与目标速度差别大那占空比修改的幅度就大,差别小那就修改幅度小。但是,这些终究是我们自己想的,在程序里边要怎么实现呢?比较高效的做法就是使用一个数学计算公式实现,该公式有一个变量: 当前速度与目标速度的速度差值(有正负值之分),公式的计算结果是占空比的修改幅度值(有正负值之分)。 一般在程序中的实现方法都是把这个数学计算公式用一个函数实现。PID 算法就是解决这个问题的数学公式。 实际上,我们不仅仅想通过数学公式实现占空比自动调整,并且是希望可以在很短的时间内就可以实现稳定在目标速度。
所以, 一般 PID 算法要实现:快准狠。
比例(P)控制
比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差(Steady-state error)。
积分(I)控制
在积分控制中,控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统(System with Steady-state Error)。为了消除稳态误差,在控制器中必须引入“积分项”。积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。因此,比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
微分(D)控制
在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。 自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因是由于存在有较大惯性组件(环节)或有滞后(delay)组件,具有抑制误差的作用,其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。 这就是说,在控制器中仅引入“比例”项往往是不够的,比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,这样,具有比例+微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象,比例+微分(PD)控制器能改善系统在调节过程中的动态特性。
5.数字PID控制
数字式 PID 控制算法可以分为位置式 PID 和增量式 PID 控制算法。
5.1位置式PID
由于计算机控制是一种采样控制,它只能根据采样时刻的偏差计算控制量,而不能像模拟控制那样连续输出控制量量,进行连续控制。 (式1-1)
公式1-1的积分项和微分项不能直接使用,必须进行离散化处理。离散化处理的方法为:以 T 作为采样周期, k 作为采样序号,则离散采样时间 kT 对应着连续时间t,用矩形法数值积分近似代替积分,用一阶后向差分近似代替微分,可作如下近似变换:
(式1-2)
上式中,为了方便表示,将类似于e(kT)简化为ek,将(式1-2)代入(式1-1)就可以得到离散的PID表达式为:
(式1-3)
(式1-4)
其中:k -> 采样序号,k=0,1,2,...; -> 第k次采样时刻的计算输出值;
-> 第k次采样时刻输入的偏差值;
-> 第k-1次采样时刻输入的偏差值;Ki -> 积分系数,Ki = Kp*T/Ti;Kd -> 微分系数,Kd = Kp*Td/T;如果采样周期足够小,则离散控制过程与连续控制过程十分接近。
5.2增量式PID
所谓增量式 PID 是指数字控制器的输出只是控制量的增量∆uk。当执行机构需要的控制量是增量,而不是位置量的绝对数值时,可以使用增量式 PID 控制算法进行控制。增量式 PID 控制算法可以通过公式 1-3推导出。由公式 1-3 可以得到控制器的第 k-1 个采样时刻的输出值为:
(式1-5)
将公式1-3与公式1-5相减并整理得到增量式PID控制算法的公式为:
(式1-6)
其中:,
,
5.3控制器参数整定
6、代码讲解
PID代码文件在Middlewares/PID.cpp中,具体内容如下:
#include "PID.h"
PID::PID()
{}void PID::update(int min_val, int max_val, float kp, float ki, float kd)
{ min_val_ = min_val;max_val_ = max_val;kp_ = kp;ki_ = ki;kd_ = kd;
}int PID::compute(int setpoint, int measured_value)
{ double error = 0;double pid = 0;//setpoint is constrained between min and max to prevent pid from having too much errorif(setpoint == 0){integral_ = 0;derivative_ = 0;prev_error_ = 0;return 0;}error = setpoint - measured_value;if(abs(error)<0.1)error=0;integral_ += error;derivative_ = error - prev_error_;if(setpoint == 0 && error == 0){integral_ = 0;}pid = (kp_ * error) + (ki_ * integral_) + (kd_ * derivative_);prev_error_ = error;return constrain(pid, min_val_, max_val_);
}
void PID::updateConstants(float kp, float ki, float kd)
{kp_ = kp;ki_ = ki;kd_ = kd;
}
代码是使用C++写的,需要自己进行实例化 。具体调用代码在moveBase_Task.cpp中
PID motor1_pid;
PID motor2_pid;
PID motor3_pid;
PID motor4_pid;
void setPidParam(void)
{switch(configParam.RobotType){case 1:{//d2 t2 motor1_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M1.K_p, configParam.p_M1.K_i,configParam.p_M1.K_d);motor2_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M2.K_p, configParam.p_M2.K_i,configParam.p_M2.K_d);}break;case 3:{//a1 转向舵机+两个减速电机motor1_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M1.K_p, configParam.p_M1.K_i,configParam.p_M1.K_d);motor2_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M2.K_p, configParam.p_M2.K_i,configParam.p_M2.K_d);}break; case 4:{//a2 转向舵机+一个动力电机if(MotorType_t == M_ESC_ENC){ motor1_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M1.K_p, configParam.p_M1.K_i,configParam.p_M1.K_d);}}break;case 5:{//o3motor1_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M1.K_p, configParam.p_M1.K_i,configParam.p_M1.K_d);motor2_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M2.K_p, configParam.p_M2.K_i,configParam.p_M2.K_d);motor3_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M3.K_p, configParam.p_M3.K_i,configParam.p_M3.K_d);}break;case 2: //d4 t4case 6: //o4case 7:{//m4motor1_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M1.K_p, configParam.p_M1.K_i,configParam.p_M1.K_d);motor2_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M2.K_p, configParam.p_M2.K_i,configParam.p_M2.K_d);motor3_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M3.K_p, configParam.p_M3.K_i,configParam.p_M3.K_d);motor4_pid.update(-configParam.Max_PWM, configParam.Max_PWM, configParam.p_M4.K_p, configParam.p_M4.K_i,configParam.p_M4.K_d);}break;}
}mDeb_p.M1.Pwm_Out = motor1_pid.compute(mDeb_p.M1.Expectations,mDeb_p.M1.Feedback);
mDeb_p.M2.Pwm_Out = motor2_pid.compute(mDeb_p.M2.Expectations,mDeb_p.M2.Feedback);
mDeb_p.M3.Pwm_Out = motor3_pid.compute(mDeb_p.M3.Expectations,mDeb_p.M3.Feedback);
mDeb_p.M4.Pwm_Out = motor4_pid.compute(mDeb_p.M4.Expectations,mDeb_p.M4.Feedback);通过函数update()对参数进行赋值,根据期望值和反馈值调用compute计算PID系统的输出PWM值。
相关文章:
手把手教你搭建ROS阿克曼转向小车之(增量式PID代码实现)
在上一篇文章中我们已经成功的把编码器的反馈值给计算出来,这篇文章将会讲解怎么使用反馈回来的速度值进行PID计算,从而闭环控制电机的速度。 PID算法介绍 1.开环控制系统 开环控制系统(open-loop control system)是指被控对象的输出(被控制量)对控制器…...
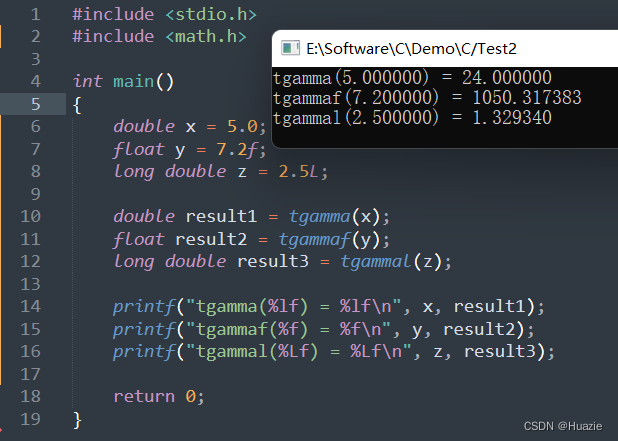
C语言函数大全-- t 开头的函数
C语言函数大全 本篇介绍C语言函数大全-- t 开头的函数 1. tan,tanf,tanl 1.1 函数说明 函数声明函数功能double tan(double x)计算 以弧度 x 为单位的角度的正切值(double)float tanf(float x)计算 以弧度 x 为单位的角度的正…...

安卓系统APP稳定性测试分析的研究报告
目录 第一章:概念 第二章:重要性 第三章:意义和作用 第四章:行业现状 第五章:常见测试方法和工具 第六章:实际测试场景 第七章:测试方案 第八章:测试方法 第九章࿱…...

【Java基础】集合
一、集合概述 为了方便对多个对象进行存储和操作,集合是一种Java容器,可以动态地把多个对象引用放入容器中 数组存储的特点 一旦初始化后,长度不可改变,元素类型不可改变提供的方法很少,对于添加、删除、获取实际元…...

【Android入门到项目实战-- 9.1】—— 传感器的使用教程
目录 传感器的定义 三大类型传感器 1、运动传感器 2、环境传感器 3、位置传感器 传感器开发框架 1、SensorManager 2、Sensor 3、SensorEvent 4、SensorEventListener 一、使用传感器开发步骤 1、获取传感器信息 1)、获取传感器管理器 2)、获取设备的传感器对象列…...
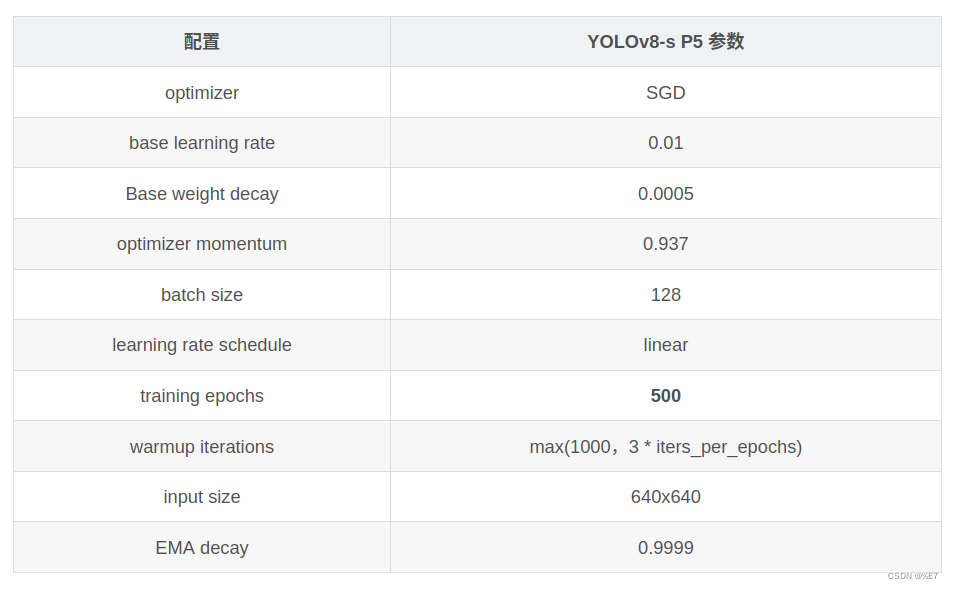
yolov8 浅记
目录 Pre: 1. YOLOv8 概述 2. 模型结构设计 3. Loss 计算 4.训练数据增强 5. 训练策略 6、部署推理 End Pre: yolo系列发布时间: 先贴一下yolo各系列的发布时间(说出来很丢人,我以为 yolox是 最新的): yoloX 2…...

前端009_类别模块_修改功能
第九章 1、需求分析2、Mock添加查询数据3、Mock修改数据4、Api调用回显数据5、提交修改后的数据6、效果1、需求分析 需求分析 当点击 编辑 按钮后,弹出编辑窗口,并查询出分类相关信息进行渲染。修改后点击 确定 提交修改后的数据。 2、Mock添加查询数据 请求URL: /article/…...

2022级吉林大学面向对象第一次上机测试
【注:解答全部为本人所写,仅供同学们学习时参考使用,请勿照搬抄袭!】 1、 1)略 2)如果main,f1,g1,g2或更多的函数之间有更为复杂的调用关系,头文件一般按怎样的规律写呢? 一般情况下…...
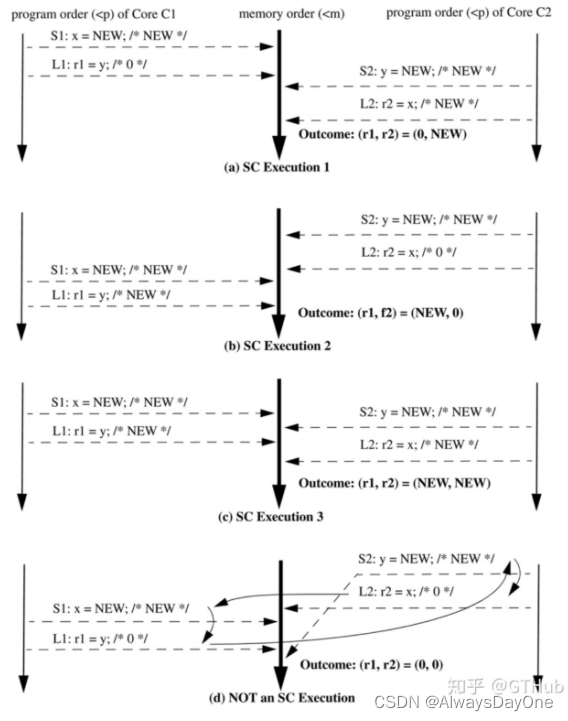
计算机体系结构总结:内存一致性模型 Memory consistency Model
存储一致性是为了保证多线程背景下的访存顺序,多线程的语句是可以交错执行,使得顺序不同产生不同的执行结果。 下面P2的输出结果可能是什么? P1, P2两个线程的语句是可以交叉执行的,比如1a, 2a, 2b, 1b;一个线程内的语…...
介绍)
高速列车运行控制系统(CTCS)介绍
1、CTCS功能 安全防护 在任何情况下防止列车无行车许可运行防止列车超速运行防止列车超过进路允许速度防止列车超过线路结构规定的速度防止列车超过机车车辆构造速度防止列车超过临时限速及紧急限速防止列车超过铁路有关运行设备的限速防止列车溜逸 人机界面 以字符、数字及…...

C#“System.Threading.ThreadStateException”类型的未经处理的异常
备忘 最近做一个功能,从主界面进入另一个界面时,数据量较大,处理信息较多,程序宕机。而且点击程序还会提示程序无响应。不得已用另一个线程显示界面。但在界面中使用控件时,报错:“System.Threading.Thread…...

为什么要交叉编译?
一、什么是交叉编译、为什么要交叉编译 1、什么是交叉编译? 交叉编译:是在一个平台上生成另一个平台上的可执行代码。比如我们在 x86 平台上,编写程序并编译成能运行在 ARM 平台的程序,编译得到的程序在 x86 平台上是不能运行的…...
java版本电子招标采购系统源码—企业战略布局下的采购
智慧寻源 多策略、多场景寻源,多种看板让寻源过程全程可监控,根据不同采购场景,采取不同寻源策略, 实现采购寻源线上化管控;同时支持公域和私域寻源。 询价比价 全程线上询比价,信息公开透明࿰…...
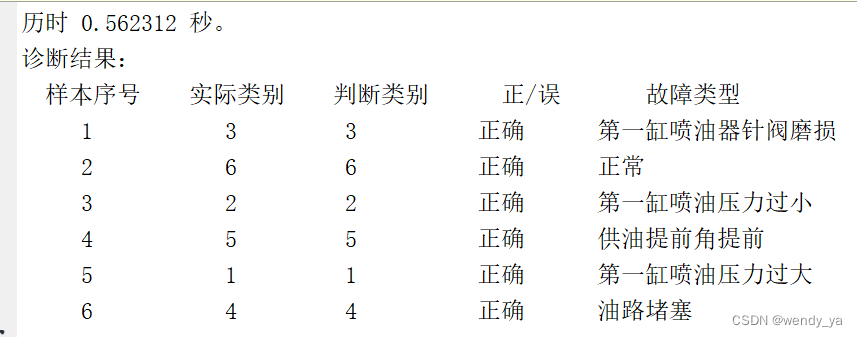
【MATLAB数据处理实用案例详解(17)】——利用概念神经网络实现柴油机故障诊断
目录 一、问题描述二、利用概念神经网络实现柴油机故障诊断原理三、算法步骤3.1 定义样本3.2 样本归一化3.3 创建网络模型3.4 测试3.5 显示结果 四、运行结果五、完整代码 一、问题描述 柴油机的结构较为复杂,工作状况非常恶劣,因此发生故障的可能性较大…...

神奇字符串、密钥格式化----2023/5/6
神奇字符串----2023/5/6 神奇字符串 s 仅由 ‘1’ 和 ‘2’ 组成,并需要遵守下面的规则: 神奇字符串 s 的神奇之处在于,串联字符串中 ‘1’ 和 ‘2’ 的连续出现次数可以生成该字符串。 s 的前几个元素是 s “1221121221221121122……” 。…...

STM32F4_十进制和BCD码的转换
目录 前言 1. BCD码 2. BCD码和十进制转换的算法 前言 最近在学习STM32单片机(不仅仅是32)的RTC实时时钟系统的过程中,需要配置时钟的时间、日期;这些都需要实现BCD码和十进制之间进行转换。这里和大家一起学习BCD码和十进制之…...
)
random — 伪随机数生成器(史上总结最全)
目的:实现几种类型的伪随机数生成器。 random 模块基于 Mersenne Twister 算法提供了一个快速的伪随机数生成器。Mersenne Twister 最初开发用于为蒙特卡洛模拟器生成输入,可生成具有分布均匀,大周期的数字,使其可以广泛用于各种…...
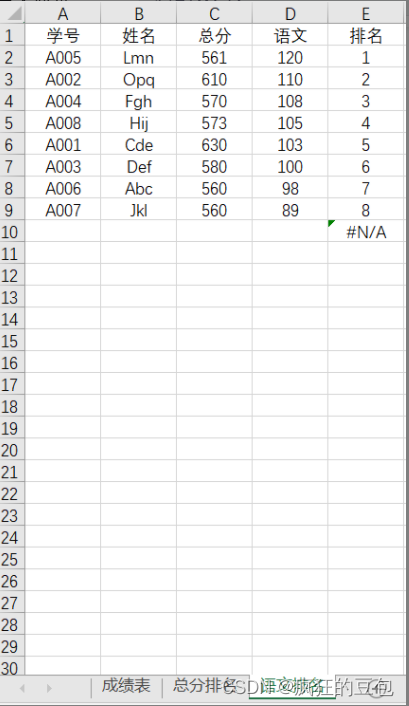
基于VBA实现成绩排序的最佳方法-解放老师的双手
作为一名老师,每到期末就要面对一件让人头疼的事情——成绩表统计。 首先,要收集每个学生的考试成绩。这需要花费大量的时间和精力,因为每个学生都有多门科目的成绩需要统计。 其次,要将每个学生的成绩录入到电子表格中。这看起来…...

OCAF如何实现引用关系和拓扑关系
在 OpenCASCADE 中,TDF_Label 是用来保存对象及其属性的基本单元。TDF_Label 可以通过添加不同类型的属性来保存不同的数据类型。属性是继承自 TDF_Attribute 类的对象,每个属性都有一个唯一的标识符(GUID)来识别其类型。TDF_Label是OpenCASCADE中用来管理数据的标签类,它…...

自动创建设备节点
在成功加载驱动模块之后,还需要使用 mknod命令创建设备节点,才能在/dev目录下创建对应的设备文件。自动创建设备节点的功能需要依赖 mdev 设备管理机制,在使用 buildroot 构建 rootfs 的时候,会默认构建 mdev 的功能,m…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
