【51单片机】点亮一个LED灯(看开发板原理图十分重要)
🎊专栏【51单片机】
🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。
🎆音乐分享【The Right Path】
🥰大一同学小吉,欢迎并且感谢大家指出我的问题🥰
目录
🍔基础内容
🏳️🌈sbit:特殊功能位声明
🏳️🌈注意
🎆方法一
🍔现象&&代码
🎊点亮一个
🎈现象
🎈代码
🎊点亮两个
🎈现象
🎈代码
🎊点亮三个
🎈现象
🎈代码
🎆方法二
🍔现象&&代码
🎊点亮一个
🎈现象
🎈代码
🎊点亮两个
🎈现象
🎈代码
🏳️🌈总结(非常重要)
🍔基础内容
🏳️🌈sbit:特殊功能位声明
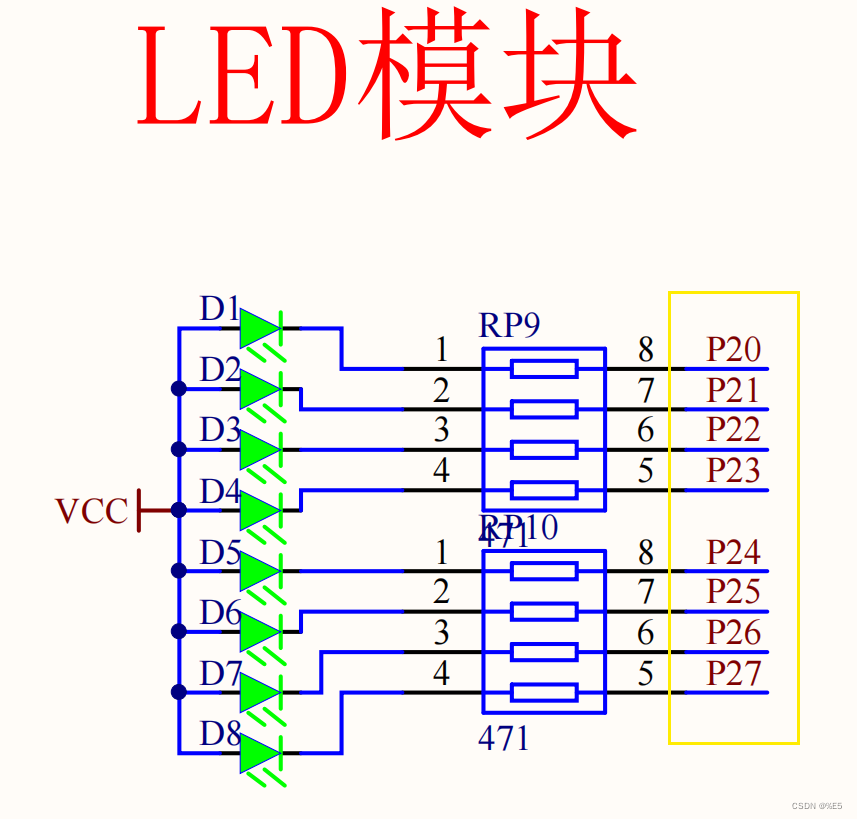
sbit 变量名=地址值;在给某个引脚取名的时候经常会用到。如上面对LED管脚的定义sbit led=P2^0。
如下图,就可以声明为
P2^0 P2^1 P2^2 P2^3等
🏳️🌈注意
⭐声明引脚必须要按照电路原理图上面给的引脚来声明,比如P0^1就是错的
🎆方法一
使用sbit
🍔现象&&代码
🎊点亮一个
🎈现象

🎈代码
#include <REGX52.H>sbit led=P2^0; //将单片机的P2.0端口定义为led(当然也可以定义其他端口)void main()
{while(1) {led=0; //低电平}
}⭐可以看到LED模块是共阳极的,所以引脚(P2^0)要为0(低电平)
🎊点亮两个
🎈现象

🎈代码
#include <REGX52.H>sbit led1=P2^0; //将单片机的P2.0端口定义为led(当然也可以定义其他端口)
sbit led2=P2^1;
void main()
{while(1) {led1=0; //低电平led2=0;}
}🎊点亮三个
🎈现象

🎈代码
#include <REGX52.H>sbit led1=P2^0; //将单片机的P2.0端口定义为led(当然也可以定义其他端口)
sbit led2=P2^1;
sbit led3=P2^2;
void main()
{while(1) {led1=0; //低电平led2=0;led3=0;}
}可以发现,声明不同的引脚,可以点亮不同的灯
🎆方法二
使用二进制
🍔现象&&代码
🎊点亮一个
🎈现象

🎈代码
#include <REGX52.H>void main()
{while(1) {P2=0xFE; }
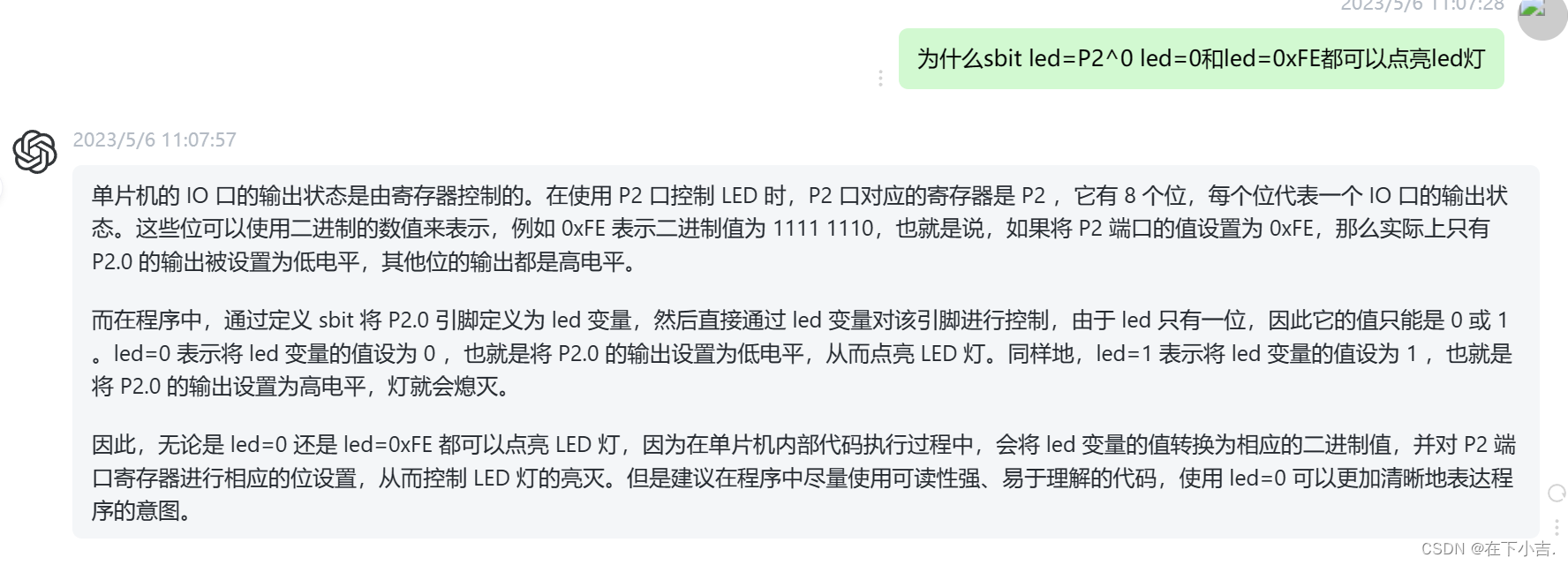
}0xEF对应二进制1111 1110,最低位为0,所以P2.0 的输出被设置为低电平,其他位的输出都是高电平
🎊点亮两个
🎈现象

🎈代码
#include <REGX52.H>void main()
{while(1) {P2=0xFE; //1111 1110P2=0xFD; //1111 1101}
}🏳️🌈总结(非常重要)
上面介绍了两种方式点亮LED灯,下面来说说一些注意事项
1.要看原理图,因为原理图上面的LED是P2的,所以如果写为P3=0xFE,就不能亮
2.sbit和使用二进制其实有一定的关联
比如P2=0xFE,对应二进制1111 1110,就是P2.0,和sbit led=P2^0是一样的
🥰如果大家有不明白的地方,或者文章有问题,欢迎大家在评论区讨论,指正🥰
相关文章:

【51单片机】点亮一个LED灯(看开发板原理图十分重要)
🎊专栏【51单片机】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【The Right Path】 🥰大一同学小吉,欢迎并且感谢大家指出我的问题🥰 目录 🍔基础内容 🏳…...
数据可视化工具 - ECharts以及柱状图的编写
1 快速上手 引入echarts 插件文件到html页面中 <head><meta charset"utf-8"/><title>ECharts</title><!-- step1 引入刚刚下载的 ECharts 文件 --><script src"./echarts.js"></script> </head>准备一个…...
【AI绘画】——Midjourney关键词格式解析(常用参数分享)
目前在AI绘画模型中,Midjourney的效果是公认的top级别,但同时也是相对较难使用的,对小白来说比较难上手,主要就在于Mj没有webui,不能选择参数,怎么找到这些隐藏参数并且触发它是用好Mj的第一步。 今天就来…...

操作符知识点大全(简洁,全面,含使用场景,演示,代码)
目录 一.算术操作符 1.要点: 二.负数原码,反码,补码的互推 1.按位取反操作符:~(二进制位) 2.原反补互推演示 三.进制位的表示 1.不同进制位的特征: 2.二进制位表示 3.整型的二进制表…...

华工研究生语音课
这门课讲啥 语音蕴含的信息、语音识别的目的 语音的准平稳性、分帧、预加重、时域特征分析(能量和过零率)、端点检测(双门限法) 语音的基频及检测(主要是自相关法、野点的处理) 声音的产生过程…...

KingbaseES 原生XML系列二 -- XML数据操作函数
KingbaseES 原生XML系列二--XML数据操作函数(DELETEXML,APPENDCHILDXML,INSERTCHILDXML,INSERTCHILDXMLAFTER,INSERTCHILDXMLBEFORE,INSERTXMLAFTER,INSERTXMLBEFORE,UPDATEXML) XML的简单使其易于在任何应用程序中读写数据,这使XML很快成为数据交换的一种公共语言。…...
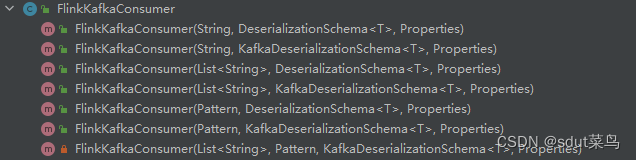
【Flink】DataStream API使用之源算子(Source)
源算子 创建环境之后,就可以构建数据的业务处理逻辑了,Flink可以从各种来源获取数据,然后构建DataStream进项转换。一般将数据的输入来源称为数据源(data source),而读取数据的算子就叫做源算子(…...
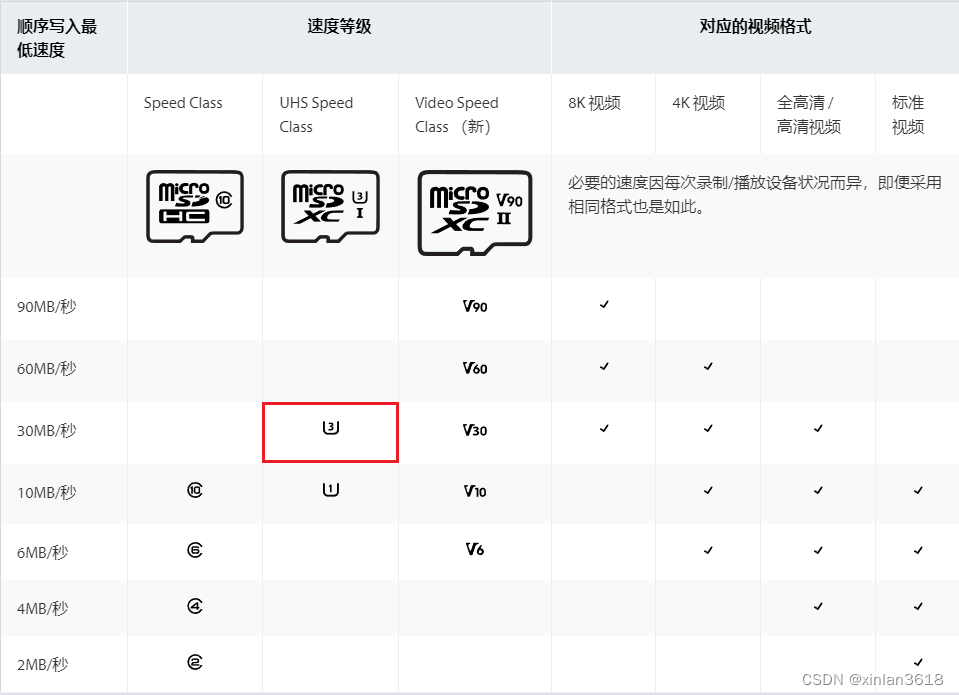
树莓派硬件介绍及配件选择
目录 树莓派Datasheet下载地址: Raspberry 4B 外观图: 技术规格书: 性能介绍: 树莓派配件选用 电源的选用: 树莓派外壳选用: 内存卡/U盘选用 树莓派Datasheet下载地址: Raspberry Pi …...
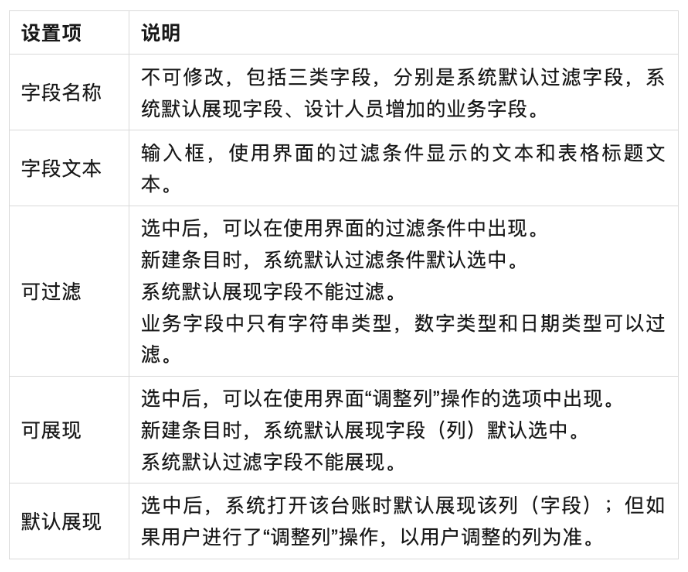
O2OA (翱途) 平台 V8.0 发布新增数据台账能力
亲爱的小伙伴们,O2OA (翱途) 平台开发团队经过几个月的持续努力,实现功能的新增、优化以及问题的修复。2023 年度 V8.0 版本已正式发布。欢迎大家到 O2OA 的官网上下载进行体验,也希望大家在藕粉社区里多提宝贵建议。本篇我们先为大家介绍应用…...

数控解锁怎么解 数控系统解锁解密
Amazon Fargate 在中国区正式落地,因 数控解锁使用 Serverless 架构,更加适合对性能要求不敏感的服务使用,Pyroscope 是一款基于 Golang 开发的应用程序性能分析工具,Pyroscope 的服务端为无状态服务且性能要求不敏感,…...
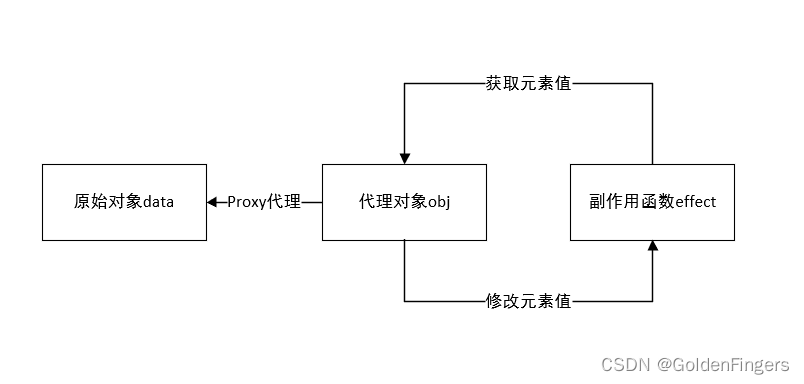
3.0 响应式系统的设计与实现
1、Proxy代理对象 Proxy用于对一个普通对象代理,实现对象的拦截和自定义,如拦截其赋值、枚举、函数调用等。里面包含了很多组捕获器(trap),在代理对象执行相应的操作时捕获,然后在内部实现自定义。 const…...
Rust 快速入门60分① 看完这篇就能写代码了
Rust 一门赋予每个人构建可靠且高效软件能力的语言https://hannyang.blog.csdn.net/article/details/130467813?spm1001.2014.3001.5502关于Rust安装等内容请参考上文链接,写完上文就在考虑写点关于Rust的入门文章,本专辑将直接从Rust基础入门内容开始讲…...

【5.JS基础-JavaScript的DOM操作】
1 认识DOM和BOM 所以我们学习DOM,就是在学习如何通过JavaScript对文档进行操作的; DOM Tree的理解 DOM的学习顺序 DOM的继承关系图 2 document对象 3 节点(Node)之间的导航(navigator) 4 元素࿰…...

【大数据之Hadoop】二十九、HDFS存储优化
纠删码和异构存储测试需要5台虚拟机。准备另外一套5台服务器集群。 环境准备: (1)克隆hadoop105为hadoop106,修改ip地址和hostname,然后重启。 vim /etc/sysconfig/network-scripts/ifcfg-ens33 vim /etc/hostname r…...
SuperMap GIS基础产品组件GIS FAQ集锦(2)
SuperMap GIS基础产品组件GIS FAQ集锦(2) 【iObjects for Spark】读取GDB参数该如何填写? 【解决办法】可参考以下示例: val GDB_params new util.HashMapString, java.io.Serializable GDB_params.put(FeatureRDDProviderParam…...
函数中整型格式说明符详解)
C语言printf()函数中整型格式说明符详解
每个整型在printf()函数中对应不同的格式说明符,以实现该整型的打印输出。格式说明符必须使用小写。现在让我们看看各个整型及其格式说明符: 短整型(short) 10进制:%hd16进制:无负数格式,正数使用%hx8进制:无负数格式,正数使用%ho c short s 34; printf("%hd", s…...
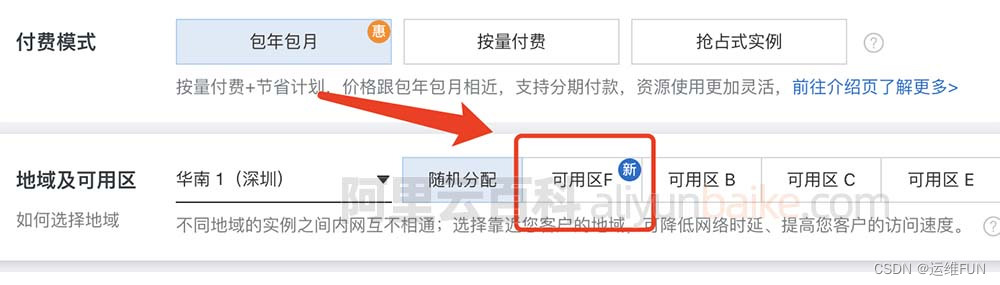
阿里云服务器地域和可用区怎么选择合适?
阿里云服务器地域和可用区怎么选择?地域是指云服务器所在物理数据中心的位置,地域选择就近选择,访客距离地域所在城市越近网络延迟越低,速度就越快;可用区是指同一个地域下,网络和电力相互独立的区域&#…...
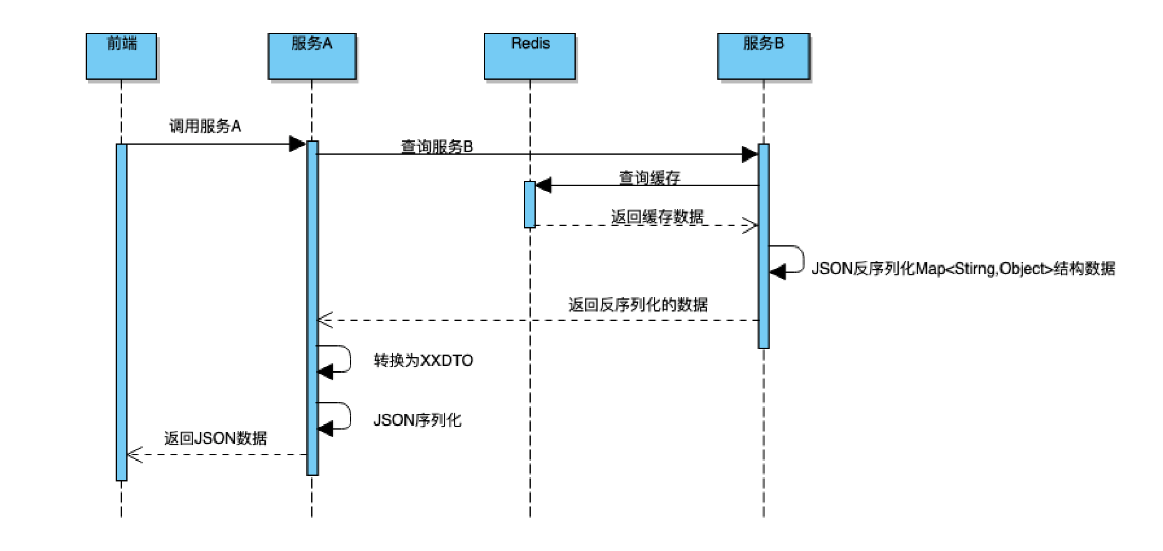
Java序列化引发的血案
1、引言 阿里巴巴Java开发手册在第一章节,编程规约中OOP规约的第15条提到: **【强制】**序列化类新增属性时,请不要修改serialVersionUID字段,避免反序列失败;如果完全不兼容升级,避免反序列化混乱&#x…...

为Linux系统添加一块新硬盘,并扩展根目录容量
我的原来ubuntu20.04系统装的时候不是LVM格式的分区, 所以先将新硬盘转成LVM,再将原来的系统dd到新硬盘,从新硬盘的分区启动,之后再将原来的分区转成LVM,在融入进来 1:将新硬盘制作成 LVM分区 我的新硬盘…...

树莓派Opencv调用摄像头(Raspberry Pi 11)
前言:本人初玩树莓派opencv,使用的是树莓派Raspberry Pi OS 11,系统若不一致请慎用,本文主要记录在树莓派上通过Opencv打开摄像头的经验。 1、系统版本 进入树莓派,打开终端输入以下代码(查看系统的版本&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
