每天一道算法练习题--Day21 第一章 --算法专题 --- ----------位运算
我这里总结了几道位运算的题目分享给大家,分别是 136 和 137, 260 和 645, 总共加起来四道题。 四道题全部都是位运算的套路,如果你想练习位运算的话,不要错过哦~~
前菜
开始之前我们先了解下异或,后面会用到。
异或的性质
两个数字异或的结果a^b是将 a 和 b 的二进制每一位进行运算,得出的数字。 运算的逻辑是果同一位的数字相同则为 0,不同则为 1。
异或的规律:
- 任何数和本身异或则为0
- 任何数和 0 异或是本身
- 异或运算满足交换律,即:a ^ b ^ c = a ^ c ^ b
OK,我们来看下这三道题吧。
136. 只出现一次的数字 1
题目大意是除了一个数字出现一次,其他都出现了两次,让我们找到出现一次的数。我们执行一次全员异或即可。
class Solution:def singleNumber(self, nums: List[int]) -> int:single_number = 0for num in nums:single_number ^= numreturn single_number
复杂度分析
时间复杂度: O ( N ) O(N) O(N),其中 N 为数组长度。
空间复杂度: O ( 1 ) O(1) O(1)
137. 只出现一次的数字 2
题目大意是除了一个数字出现一次,其他都出现了三次,让我们找到出现一次的数。 灵活运用位运算是本题的关键。
Python3:
class Solution:def singleNumber(self, nums: List[int]) -> int:res = 0for i in range(32):cnt = 0 # 记录当前 bit 有多少个1**加粗样式** bit = 1 << i # 记录当前要操作的 bitfor num in nums:if num & bit != 0:cnt += 1if cnt % 3 != 0:# 不等于0说明唯一出现的数字在这个 bit 上是1res |= bitreturn res - 2 ** 32 if res > 2 ** 31 - 1 else res
- 为什么 Python 最后需要对返回值进行判断?
如果不这么做的话测试用例是[-2,-2,1,1,-3,1,-3,-3,-4,-2] 的时候,就会输出 4294967292。 其原因在于 Python 是动态类型语言,在这种情况下其会将符号位置的 1 看成了值,而不是当作符号“负数”。 这是不对的。 正确答案应该是 - 4,-4 的二进制码是 1111…100,就变成 2^32-4=4294967292,解决办法就是 减去 2 ** 32 。
之所以这样不会有问题的原因还在于题目限定的数组范围不会超过 2 ** 32
JavaScript:
var singleNumber = function (nums) {let res = 0;for (let i = 0; i < 32; i++) {let cnt = 0;let bit = 1 << i;for (let j = 0; j < nums.length; j++) {if (nums[j] & bit) cnt++;}if (cnt % 3 != 0) res = res | bit;}return res;
};
复杂度分析
时间复杂度: O ( N ) O(N) O(N),其中 N 为数组长度。
空间复杂度: O ( 1 ) O(1) O(1)
上述感觉这种方法他没说清楚,特此补充完整,
方法二:依次确定每一个二进制位
思路与算法

细节

代码
class Solution {public int singleNumber(int[] nums) {int ans = 0;for (int i = 0; i < 32; ++i) {int total = 0;for (int num: nums) {total += ((num >> i) & 1);}if (total % 3 != 0) {ans |= (1 << i);}}return ans;}
}作者:LeetCode-Solution
链接:https://leetcode.cn/problems/single-number-ii/solution/zhi-chu-xian-yi-ci-de-shu-zi-ii-by-leetc-23t6/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
645. 错误的集合
和上面的137. 只出现一次的数字2思路一样。这题没有限制空间复杂度,因此直接 hashmap 存储一下没问题。 不多说了,我们来看一种空间复杂度 O ( 1 ) O(1) O(1)的解法。
由于和137. 只出现一次的数字2思路基本一样,我直接复用了代码。具体思路是,将 nums 的所有索引提取出一个数组 idx,那么由 idx 和 nums 组成的数组构成 singleNumbers 的输入,其输出是唯二不同的两个数。
但是我们不知道哪个是缺失的,哪个是重复的,因此我们需要重新进行一次遍历,判断出哪个是缺失的,哪个是重复的。
class Solution:def singleNumbers(self, nums: List[int]) -> List[int]:ret = 0 # 所有数字异或的结果a = 0b = 0for n in nums:ret ^= n# 找到第一位不是0的h = 1while(ret & h == 0):h <<= 1for n in nums:# 根据该位是否为0将其分为两组if (h & n == 0):a ^= nelse:b ^= nreturn [a, b]def findErrorNums(self, nums: List[int]) -> List[int]:nums = [0] + numsidx = []for i in range(len(nums)):idx.append(i)a, b = self.singleNumbers(nums + idx)for num in nums:if a == num:return [a, b]return [b, a]
复杂度分析
时间复杂度: O ( N ) O(N) O(N)
空间复杂度: O ( 1 ) O(1) O(1)
260. 只出现一次的数字 3
题目大意是除了两个数字出现一次,其他都出现了两次,让我们找到这个两个数。
我们进行一次全员异或操作,得到的结果就是那两个只出现一次的不同的数字的异或结果。
我们刚才讲了异或的规律中有一个任何数和本身异或则为0, 因此我们的思路是能不能将这两个不同的数字分成两组 A 和 B。 分组需要满足两个条件.
- 两个独特的的数字分成不同组
- 相同的数字分成相同组
这样每一组的数据进行异或即可得到那两个数字。
问题的关键点是我们怎么进行分组呢?
由于异或的性质是,同一位相同则为 0,不同则为 1. 我们将所有数字异或的结果一定不是 0,也就是说至少有一位是 1.
我们随便取一个, 分组的依据就来了, 就是你取的那一位是 0 分成 1 组,那一位是 1 的分成一组。 这样肯定能保证2. 相同的数字分成相同组, 不同的数字会被分成不同组么。 很明显当然可以, 因此我们选择是 1,也就是 说两个独特的的数字在那一位一定是不同的,因此两个独特元素一定会被分成不同组。
class Solution:def singleNumbers(self, nums: List[int]) -> List[int]:ret = 0 # 所有数字异或的结果a = 0b = 0for n in nums:ret ^= n# 找到第一位不是0的h = 1while(ret & h == 0):h <<= 1for n in nums:# 根据该位是否为0将其分为两组if (h & n == 0):a ^= nelse:b ^= nreturn [a, b]
复杂度分析
时间复杂度: O ( N ) O(N) O(N),其中 N 为数组长度。
空间复杂度: O ( 1 ) O(1) O(1)

方法二:位运算
思路与算法


代码
class Solution {public int[] singleNumber(int[] nums) {int xorsum = 0;for (int num : nums) {xorsum ^= num;}// 防止溢出int lsb = (xorsum == Integer.MIN_VALUE ? xorsum : xorsum & (-xorsum));int type1 = 0, type2 = 0;for (int num : nums) {if ((num & lsb) != 0) {type1 ^= num;} else {type2 ^= num;}}return new int[]{type1, type2};}
}作者:LeetCode-Solution
链接:https://leetcode.cn/problems/single-number-iii/solution/zhi-chu-xian-yi-ci-de-shu-zi-iii-by-leet-4i8e/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

每天一道算法练习题--Day21 第一章 --算法专题 --- ----------位运算
我这里总结了几道位运算的题目分享给大家,分别是 136 和 137, 260 和 645, 总共加起来四道题。 四道题全部都是位运算的套路,如果你想练习位运算的话,不要错过哦~~ 前菜 开始之前我们先了解下…...
D1. LuoTianyi and the Floating Islands (Easy Version)(树形dp)
Problem - D1 - Codeforces 这是问题的简化版本。唯一的区别在于在该版本中k≤min(n,3)。只有在两个版本的问题都解决后,才能进行黑客攻击。 琴音和漂浮的岛屿。 洛天依现在生活在一个有n个漂浮岛屿的世界里。这些漂浮岛屿由n−1个无向航线连接,任意两个…...

rk3588移植ubuntu server
ubuntu server 18.04 arm版本. 1、使用qemu运行 安装qemu-system-aarch64 sudo apt install -y qemu-system-arm 2、下载ubuntu server Index of /releases/18.04.3 3、创建虚拟磁盘 qemu-img create ubuntuimg.img 40G 4、创建虚拟机 弹出界面,直接回车选…...

如何更好地刷力扣
之前刷力扣是一口气看很多题目,打算时不时看一会题解,逐渐熟悉套路,争取背过,最后就可以写出来了。我个人是背知识比较喜欢这种方法,但后来发现根本不适用 算法题本身就比较复杂,不经过实际写代码中的思考…...

上采样和下采样
首先,谈谈不平衡数据集。不平衡数据集指的是训练数据中不同类别的样本数量差别较大的情况。在这种情况下,模型容易出现偏差,导致模型对数量较少的类别预测效果不佳。 为了解决这个问题,可以使用上采样和下采样等方法来调整数据集…...

小猪,信息论与我们的生活
前言 动态规划是大家都熟悉与陌生的知识,非常灵活多变,我自己也不敢说自己掌握了,今天给大家介绍一道题,不仅局限于动态规划做题,还会上升到信息论,乃至于启发自己认知世界的角度 因为比较难,本…...
【鸿蒙应用ArkTS开发系列】- http网络库使用讲解和封装
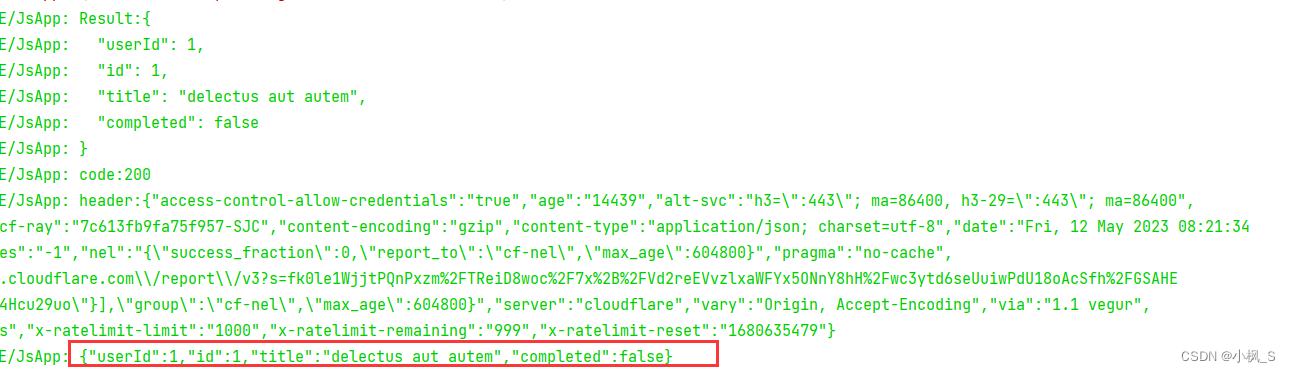
目录 前言http网络库组件介绍http网络库封装创建Har Module创建RequestOption 配置类创建HttpCore核心类创建HttpManager核心类对外组件导出添加网络权限 http网络库依赖和使用依赖http网络库(httpLibrary)使用http网络库(httpLibrary&#x…...

【Java零基础入门篇】第 ⑥ 期 - 异常处理
博主:命运之光 专栏:Java零基础入门 学习目标 掌握异常的概念,Java中的常见异常类; 掌握Java中如何捕获和处理异常; 掌握自定义异常类及其使用; 目录 异常概述 异常体系 常见的异常 Java的异常处理机制…...

计算职工工资
目录 问题描述 程序设计 问题描述 【问题描述】 给定N个职员的信息,包括姓名、基本工资、浮动工资和支出,要求编写程序顺序输出每位职员的姓名和实发工资(实发工资=基本工资+浮动工资-支出)。 【输入形式】 输入在一行中给出正整数N。随后N行,每行给出一位职员的信息,…...

2019年上半年软件设计师下午试题
试题四(共 15 分) 阅读下列说明和 C 代码,回答问题 1 至 3,将解答写在答题纸的对应栏内 【说明】 n 皇后问题描述为:在一个 n*n 的棋盘上摆放 n 个皇后,要求任意两个皇后不能冲突, 即任意两个皇后不在同一行、同一列或者同一斜…...

IS200TPROH1BCB用于工业应用和电力分配等。高压型隔离开关用于变电站
IS200TPROH1BCB用于工业应用和电力分配等。高压型隔离开关用于变电站 什么是隔离器,它与断路器有何不同 什么是隔离器,为什么要使用隔离器 隔离器是一种开关装置,它可以手动或自动操作,隔离一部分电能。隔离器可用于在无负载情…...
【MySql】数据库 select 进阶
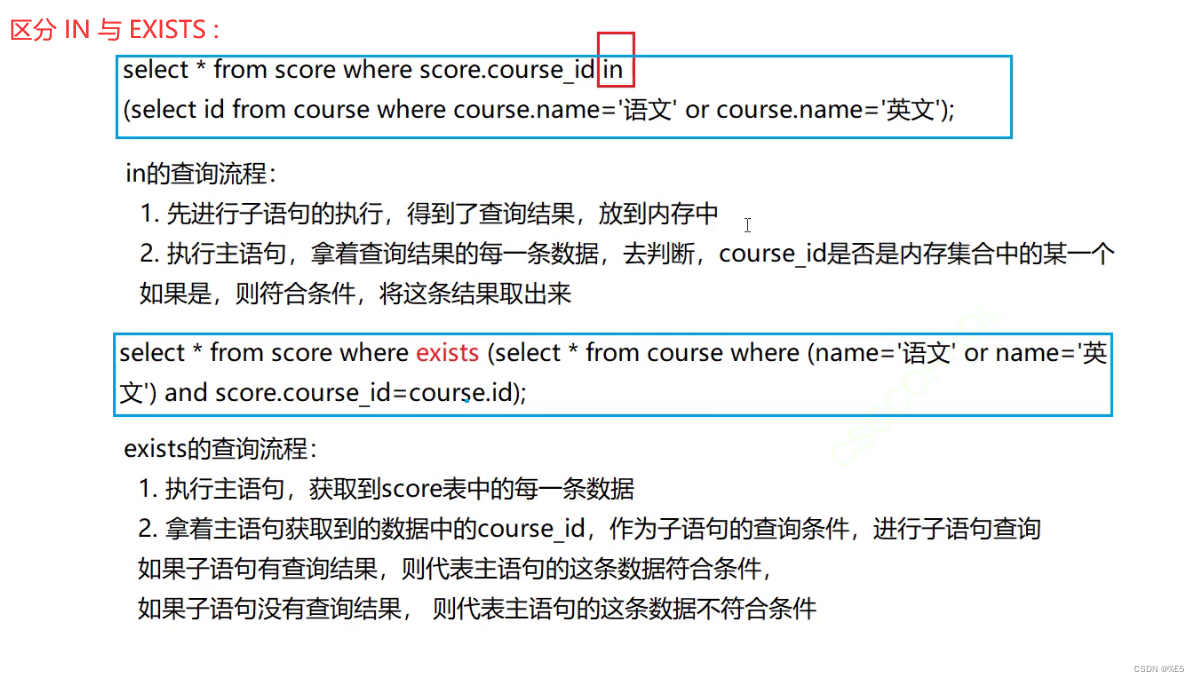
数据库 数据库表的设计ER 关系图三大范式 聚合函数与分组查询聚合函数 (count、sum、avg、max、min)分组查询 group by fields....having....(条件) 多表联查内连接外连接(左连接,右连接)自连接子查询合并查询 UNION 数据库表的设计 ER 关系…...

CVPR 2023 | VoxelNeXt实现全稀疏3D检测跟踪,还能结合Seg Anything
在本文中,研究者提出了一个完全稀疏且以体素为基础的3D物体检测和跟踪框架VoxelNeXt。它采用简单的技术,运行快速,没有太多额外的成本,并且可以在没有NMS后处理的情况下以优雅的方式工作。VoxelNeXt在大规模数据集nuScenes、Waymo…...
本地使用3台centos7虚拟机搭建K8S集群教程
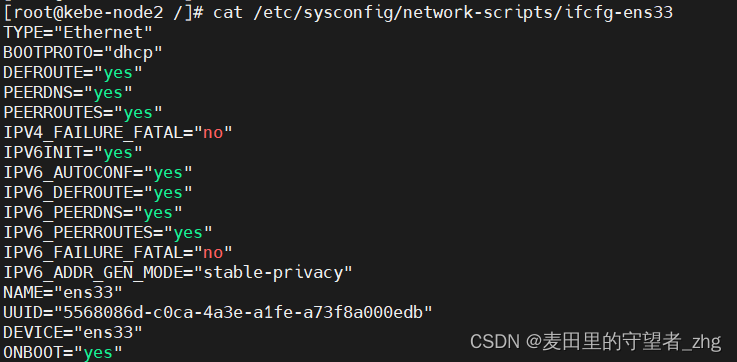
第一步 准备3台centos7虚拟机 3台虚拟机与主机的网络模式都是桥接的模式,也就是他们都是一台独立的“主机” (1)kebe-master的配置 虚拟机配置: 网络配置: (2)kebe-node1的配置 虚拟机配…...

NVIDIA CUDA驱动安装
1 引言 因为笔记本电脑上运行Milvus图像检索代码,需要安装CUDA驱动。电脑显卡型号是NVIDIA GeForce GTX 1050 Ti Mobile, 操作系统是Ubuntu 20.04,内核版本为Linux 5.15.0-72-generic。 2 CUDA驱动测试 参考网上的资料:https://blog.csdn.…...

python 从excel中获取需要执行的用例
classmethod def get_excel_data(cls, excel_name, sheet_name, case_numNone):"""读取excel文件的方法:param excel_name: 文件名称:param sheet_name: sheet页的名称:param case_name: 执行的case名称:return:"""def get_row_data(table, row)…...

Web3中文|乱花渐欲meme人眼,BRC-20总市值逼近10亿美元
现在的Web3加密市场,用“乱花渐欲meme人眼”来形容再合适不过了。 何为meme? “meme”这个词大概很多人都不知道如何正确发音,并且一看到它就会和狗狗币Dogecoin等联系在一起。那它究竟从何而来呢? Meme:[mi:m]&#x…...

盖雅案例入选「首届人力资源服务国际贸易交流合作大会20项创新经验」
近日,首届人力资源服务国际贸易交流合作大会顺利召开。为激励企业在人力资源服务贸易领域不断创新,加快培育对外贸易新业态、新模式,形成人力资源服务领域国际竞争新优势,大会评选出了「首届人力资源服务国际贸易交流合作大会20项…...

[论文笔记]SimMIM:a Simple Framework for Masked Image Modeling
文章地址:https://arxiv.org/abs/2111.09886 代码地址:https://github.com/microsoft/SimMIM 文章目录 摘要文章思路创新点文章框架Masking strategyPrediction headPrediction targetEvaluation protocols 性能实验实验设置Mask 策略预测头目标分辨率预…...
----索引/视图/范式)
mysql从零开始(4)----索引/视图/范式
接上文 mysql从零开始(3) 索引 索引是在数据库表的字段上添加的,是为了提高查询效率存在的一种机制。一张表的一个字段可以添加一个索引,也可以多个字段联合起来添加索引。索引相当于一本书的目录,是为了缩小扫描范围…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
