几种内部排序算法的cpp代码实现与分析
零、测试函数
typedef void (*SortFunc) (int*&, int);inline void swap(int &a, int &b) {int tmp = a;a = b;b = tmp;
}inline void printArr(int* a, int n) {for (int k = 0; k < n; ++k) {std::cout << a[k] << ' ';}std::cout << std::endl;
}void testSort(SortFunc func) {srand(time(nullptr));int n = rand() % 10 + 10;int* a = new int[n];for (int i = 0; i < n; ++i) {a[i] = rand() % 100;}printArr(a, n);(*func)(a, n);printArr(a, n);}
首先使用typedef将传参为(int*&, int),返回值为空的指向函数的指针类型命名为SortFunc。
其次,定义swap函数与printArr函数,swap函数会在冒泡排序、快速排序等排序算法中使用,而printArr用来输出数组。
最后,定义函数testSort,传参一个指向函数的指针,在函数体内,程序将生成一个长度取10~20之间的随机值,元素大小取0~100之间的随机值的一个数组。先对数组进行一次输出,然后调用参数func指向的函数对数组进行排序,再排序结果输出一次。
一、插入排序
插入排序的思想是每次都将一个待排序的元素按关键字大小插入前面已排序好的子序列。插入排序主要分为:直接插入排序、折半插入排序、希尔排序。
在数组已基本有序的前提下,插入排序效率最高。
1. 直接插入排序
void straightInsertionSort(int* &a, int n) {for (int i = 1; i < n; ++i) {if (a[i] >= a[i-1]) continue;int j;int tmp = a[i];for (j = i - 1; tmp < a[j] && j >= 0; --j) {a[j+1] = a[j];}a[j+1] = tmp;printArr(a, n);}}
空间复杂度:O(1)
时间复杂度:最好情况下为O(n),即数组已有序,只需进行一次遍历、最坏情况下为O(n2)、平均O(n2)
稳定性:具有稳定性
2. 折半插入排序
void binaryInsertionSort(int* &a, int n) {for (int i = 1; i < n; ++i) {if (a[i] >= a[i-1]) continue;int tmp = a[i];int low = 0;int high = i-1;int mid;while (low <= high) {mid = (low + high) / 2;if (a[mid] > tmp) {high = mid - 1;} else {low = mid + 1;}}for (int j = i; j > high+1; --j) {a[j] = a[j-1];}a[high+1] = tmp;printArr(a, n);}}
空间复杂度:O(1)
时间复杂度:最好情况下为O(n),即数组已有序,只需进行一次遍历、最坏情况下为O(n2)、平均O(nn)
稳定性:具有稳定性
3. 希尔排序
void shellSort(int* &a, int n) {int gap = n >> 1;int tmp, j;while (gap) {std::cout << "gap = " << gap << std::endl;for (int i = gap; i < n; ++i) {if (a[i] >= a[i-gap]) continue;tmp = a[i];for (j = i-gap; tmp < a[j] && j >= 0; j -= gap) {a[j+gap] = a[j];}a[j+gap] = tmp;printArr(a, n);}gap >>= 1;}}
空间复杂度:O(1)
时间复杂度:当n在某个特定范围内时,希尔排序的时间复杂度均为O(n1.3)。在最坏情况下希尔排序的时间复杂度为O(n2)。
稳定性:不具有稳定性
注意希尔排序仅适用于顺序存储的线性表
二、交换排序
1. 冒泡排序
void bubbleSort(int* &a, int n) {for (int i = 0; i < n - 1; ++i) {bool flag = true;for (int j = n - 1; j > i; --j) {if (a[j - 1] > a[j]) {swap(a[j-1], a[j]);flag = false;}}printArr(a, n);if (flag) {break;}}}
空间复杂度:O(1)
时间复杂度:最好情况下为O(n),即数组已有序,只需进行一次遍历、最坏情况下为O(n2)、平均O(n2)
稳定性:具有稳定性
2. 快速排序
void quickSort(int* &a, int high, int low = 0) {int i = low;int j = high - 1;if (i >= j) return;int pivot = a[i];while (i < j) {while (i < j && pivot < a[j]) j--;a[i] = a[j];while (i < j && a[i] < pivot) i++;a[j] = a[i];}a[i] = pivot;std::cout << "pivot = " << pivot << std::endl;quickSort(a, i, low);quickSort(a, high, i + 1);}
空间复杂度:由于快速排序是递归的,需要借助一个递归的工作栈来保存每层递归的必要信息,其容量与递归调用的最大深度保持一致。最好情况下为O(log2n);最坏情况下,即数组已有序,需要进行n-1次递归调用,空间复杂度为O(n)。平均空间复杂度为O(log2n)。
时间复杂度:最好情况下为O(nlog2n),最坏情况下为O(n2),平均为O(nlog2n)。
稳定性:不具有稳定性。
在大多数情况下,快速排序是平均性能最高的排序算法,但是排序算法并不适合对已基本接近有序的数组进行排序。
三、选择排序
1. 简单选择排序
void selectionSort(int* &a, int n) {int minIndex;for (int i = 0; i < n - 1; i++) {minIndex = i;for (int j = i + 1; j < n; j++) {if (a[j] < a[minIndex]) {minIndex = j;}}if (minIndex != i) {swap(a[i], a[minIndex]);}printArr(a, n);}}
空间复杂度:O(1)
时间复杂度:最好情况、最坏情况、平均情况下都为O(n2)
稳定性:不具有稳定性
2. 堆排序
void heapAdjust(int* &heap, int root, int n) {int tmp = heap[root]; // 暂存根节点for (int i = 2 * root + 1; i < n; i = i * 2 + 1) {if (i + 1 < n && heap[i] < heap[i+1]) {i++; // 如果右子结点更大,让指针对准右子结点}if (tmp >= heap[i]) {break;} else {heap[root] = heap[i];root = i;}}heap[root] = tmp;}void buildMaxHeap(int* &heap, int n) {for (int i = n / 2 - 1; i >= 0; --i) {heapAdjust(heap, i, n);}
}void heapSort(int* &a, int n) {buildMaxHeap(a, n);for (int i = n - 1; i > 0; --i) {swap(a[i], a[0]);heapAdjust(a, 0, i - 1);}
}
空间复杂度:O(1)
时间复杂度:建堆的时间复杂度为O(n),之后有n-1次向下调整,每次向下调整复杂度为O(h),h为堆的深度,约为log2n,故最好情况、最坏情况、平均情况下时间复杂度都为O(nlog2n)
稳定性:不具有稳定性
四、归并排序
static int* b;void merge(int* &a, int low, int mid, int high) {for (int i = low; i <= high; ++i) {b[i] = a[i];}int i, j, k;for (i = low, j = mid + 1, k = low; i <= mid && j <= high; k++) {if (b[i] <= b[j]) {a[k] = b[i++];} else {a[k] = b[j++];}}while (i <= mid) {a[k++] = b[i++];}while (j <= high) {a[k++] = b[j++];}}void mergeSort(int* &a, int low, int high) {if (low >= high) return;int mid = (low + high) / 2;mergeSort(a, low, mid);mergeSort(a, mid + 1, high);merge(a, low, mid, high);
}void mergeSort(int* &a, int n) {b = new int[n];mergeSort(a, 0, n-1);
}
空间复杂度:由于数组b的创建,空间复杂度为O(n)
时间复杂度:每趟归并复杂度为O(n)一共需要log2n次归并,所以复杂度为O(nlog2n)。
稳定性:具有稳定性。
五、基数排序
class ListNode {public:int data;ListNode* next;friend std::ostream & operator<< (std::ostream &out, ListNode &l) {ListNode* p = l.next;while(p) {out << p->data << ' ';p = p->next;}return out;}};void radixSort(ListNode* l, int d) {ListNode *p, *q;for (int i = 0; i < d; ++i) {ListNode* start[16];ListNode* end[16];bool flags[16];for (bool &flag : flags) {flag = false;}while (l->next) {p = l->next;l->next = p->next;p->next = nullptr;int x = p->data;int index = (x >> (4 * i)) & 0xf;if (flags[index]) {end[index]->next = p;end[index] = p;} else {start[index] = p;end[index] = p;flags[index] = true;}}q = l;for (int j = 0; j < 16; ++j) {if (flags[j]) {q->next = start[j];q = end[j];}}std::cout << *l << std::endl;}}
设r个队头指针队尾指针(上述代码中是16个),共进行d趟分配与收集。
空间复杂度:O®
时间复杂度:进行d趟分配与收集,一趟分配O(n),一趟收集O(r),时间复杂度为O(d(n+r))
稳定性:具有稳定性
六、总结
- 若n较小,可采用直接插入排序或简单选择排序。直接插入排序比较次数少移动次数多,简单选择排序比较次数多移动次数少。所以当记录的信息量较大时,更适合选用简单选择排序。
- 若文件初始状态已基本有序,应当使用直接插入排序或冒泡排序。
- 若n较大,则应该使用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序,目前快速排序被认为是所有基于比较的排序算法中最好的算法,当待排序关键字随机分布时,快速排序所使用的平均时间最短。堆排序相比快速排序的优点是:不需要开辟额外的内存空间。但这两种算法都是不稳定的排序算法。并且当数据已基本有序时,快速排序效率较低,不宜使用。
- 若n很大,而记录的关键字位数比较少且可分解,宜采用基数排序。
- 当记录信息量较大,为避免耗费大量时间移动记录,可使用链表作为存储结构。
相关文章:

几种内部排序算法的cpp代码实现与分析
零、测试函数 typedef void (*SortFunc) (int*&, int);inline void swap(int &a, int &b) {int tmp a;a b;b tmp; }inline void printArr(int* a, int n) {for (int k 0; k < n; k) {std::cout << a[k] << ;}std::cout << std::endl; }…...
第3天学习Docker-Docker部署常见应用(MySQL、Tomcat、Nginx、Redis、Centos)
前提须知: (1)搜索镜像命令 格式:docker search 镜像名 (2)设置Docker镜像加速器 详见文章:Docker设置ustc的镜像源(镜像加速器) 1、部署MySQL 拉取镜像(这…...

给大家介绍四款最受欢迎的抓包神器
身为互联网人,无论在平时开发还是在测试过程中,我们都不可避免的会涉及到网络安全性,如何监测网络请求,从而最大程度的保证数据的安全,需要我们了解并掌握抓包的技巧。那么何谓抓包呢?抓包就是将网络传输发…...

解决Reids过期方案 游标遍历清除Redis过期的key
游标遍历清除Redis过期的key 为什么要清除Redis过期的Key Redis的过期清理是一种懒惰的清理方案,他不会过期后立刻清除,而是在Key被访问的时候进行删除,Redis这么做的目的就是为了提高性能降低资源开销。 具体来说,一个K…...
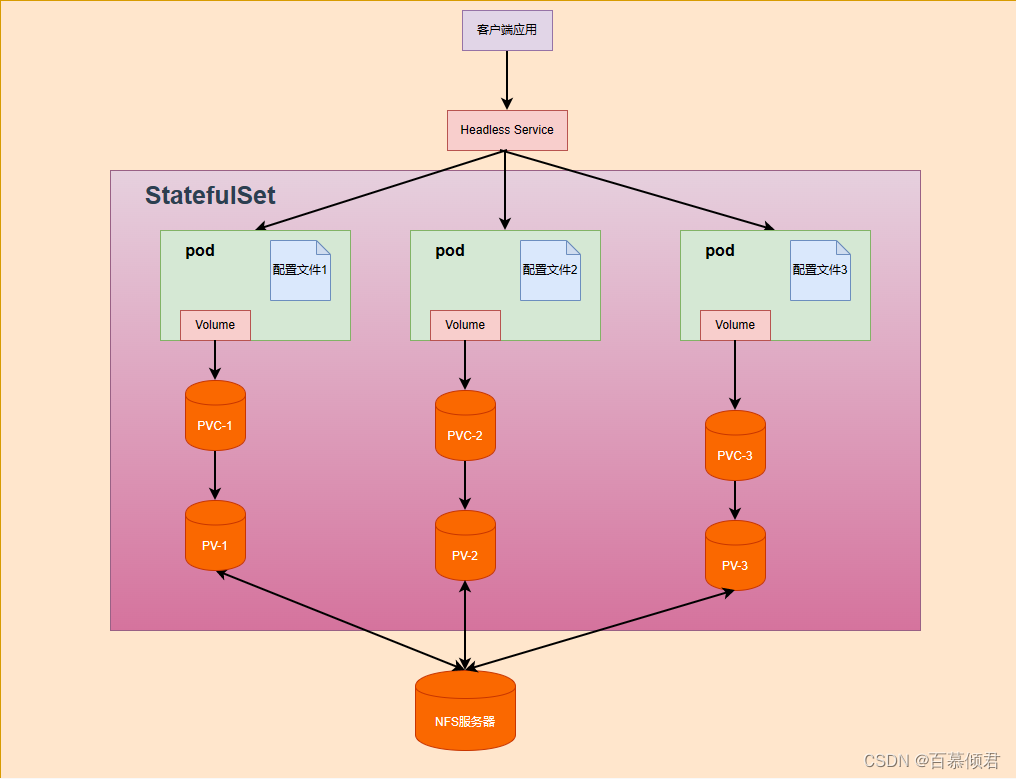
K8s基础10——数据卷、PV和PVC、StorageClass动态补给、StatefulSet控制器
文章目录 一、数据卷类型1.1 临时数据卷(节点挂载)1.2 节点数据卷(节点挂载)1.3 网络数据卷NFS1.3.1 效果测试 1.4 持久数据卷(PVC/PV)1.4.1 效果测试1.4.2 测试结论 二、PV、PVC生命周期2.1 各阶段工作原理…...

oracle系统查询~3
查看实例的基本信息 SQL> col host_name for a25 col instance_name for a15 col version for a15 col status for a10 set linesize 600 col host_name for a20 select instance_number,instance_name,host_name,version,startup_time,status,archiver f…...
— chche)
Mybatis源码(九)— chche
Mybatis中共有三级缓存,其中一级缓存默认开启,作用范围是在sqlSession对象(同一个会话),二级缓存需要手动配置开启,作用范围是在sqlSessionFactory对象下的同一个namespace范围(所以二级缓存是可…...
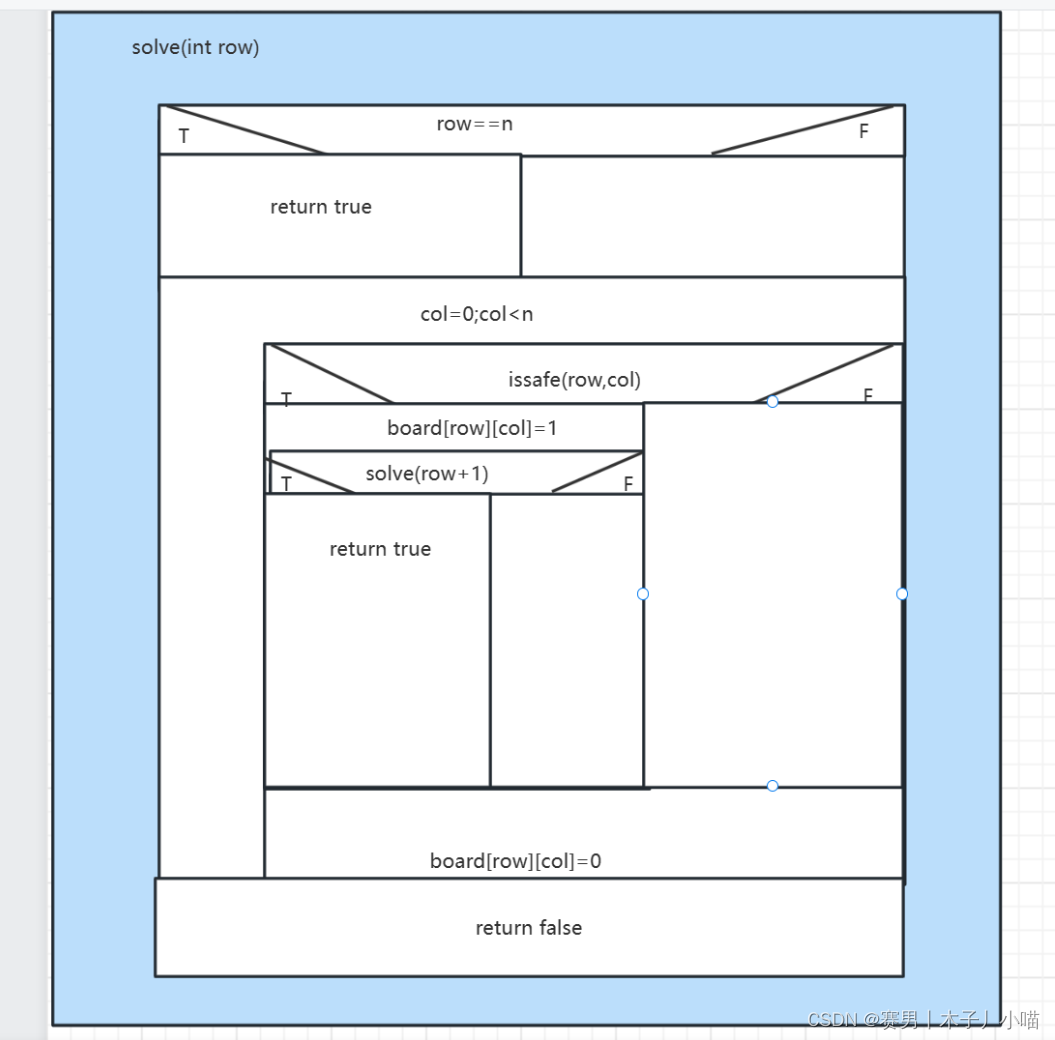
回溯法--N皇后问题
N皇后问题 一、问题描述二、示例2.1 四皇后的2个可行解2.2 过程图示 三、问题分析3.1涉及到的概念递归回溯 3.2 分析 四、 代码实现4.1 实现思路宏观:微观: 4.2 递归函数NS图4.3 代码 一、问题描述 1、按照国际象棋的规则,皇后可以攻击与之处…...

ajax请求
ajax的优点 可以无需刷新页面而与服务器进行通信允许你根据用户事件来更新部分页面内容 ajax的缺点 没有浏览历史,不能回退存在跨域问题SEO不友好 get请求 <button>点击发送请求</button><div id"result"></div><script>…...
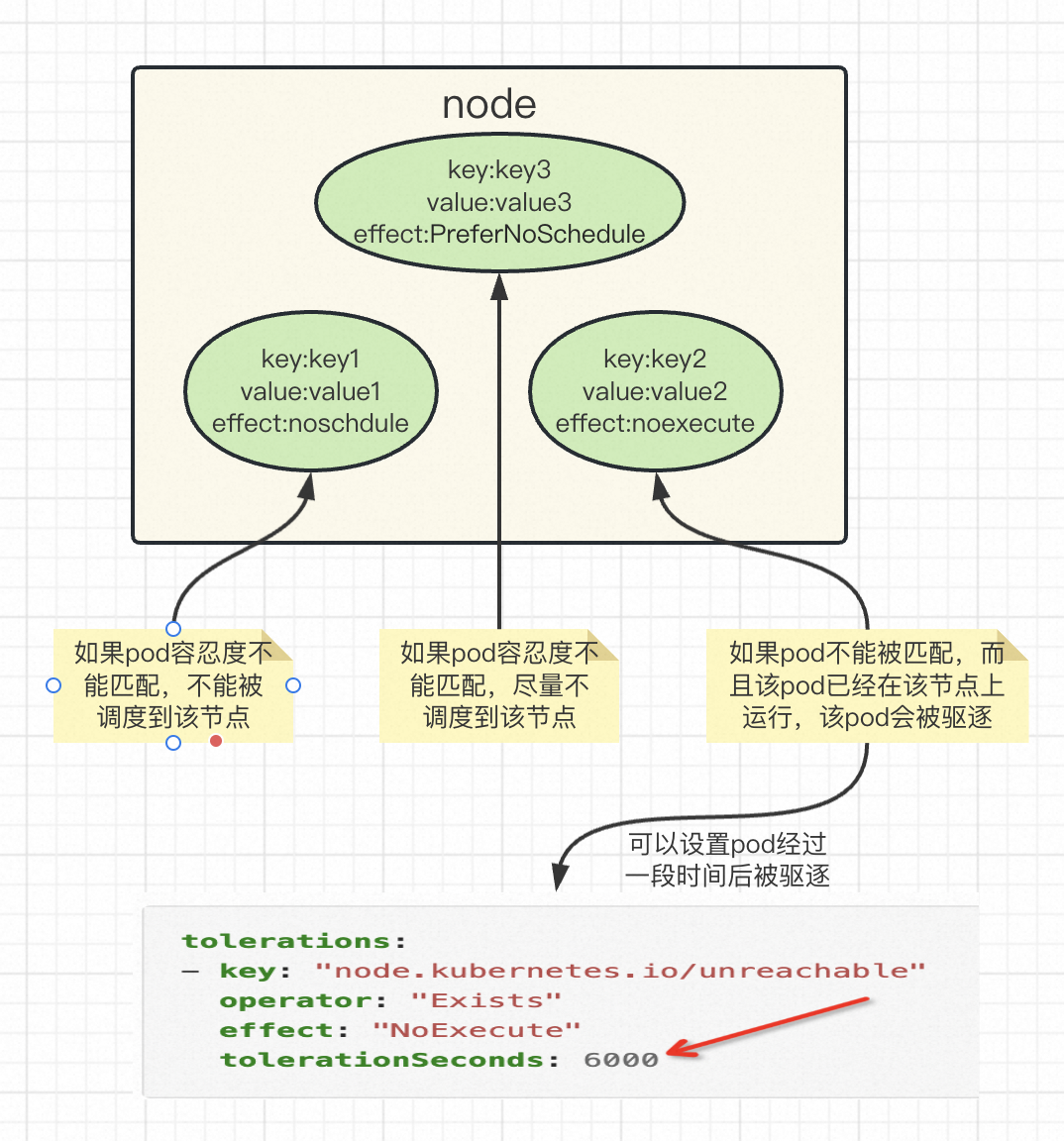
K8S系列之污点和容忍度详细分析
架构图 本篇文档主要介绍污点和容忍度的关系。 污点和容忍度 污点顾名思义就是脏的东西,给节点添加污点来限制pod调度到该节点上,如果pod可以容忍这种污点就可以被调度到有污点的节点上,如果不能容忍就不能被调度到该节点上。 污点作用于节…...

【算法】Minimum Moves to Move a Box to Their Target Location 推箱子
文章目录 Minimum Moves to Move a Box to Their Target Location 推箱子问题描述:分析代码 Tag Minimum Moves to Move a Box to Their Target Location 推箱子 问题描述: 问题 「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓…...
决策引擎平台建设方案
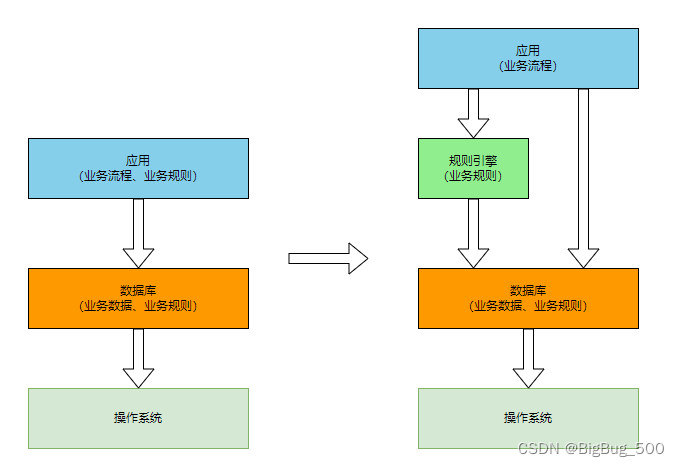
文档修订历史 时间版本主要内容2023.05.12v1.0.0初始化 1. 概述 1.1 需求 1.1.1 需求背景 当同一个业务场景中,有非常多的业务分支后,需要有非常多的 if 判断,来承载这些简单的业务逻辑,但随着业务的发展,业务逐渐…...
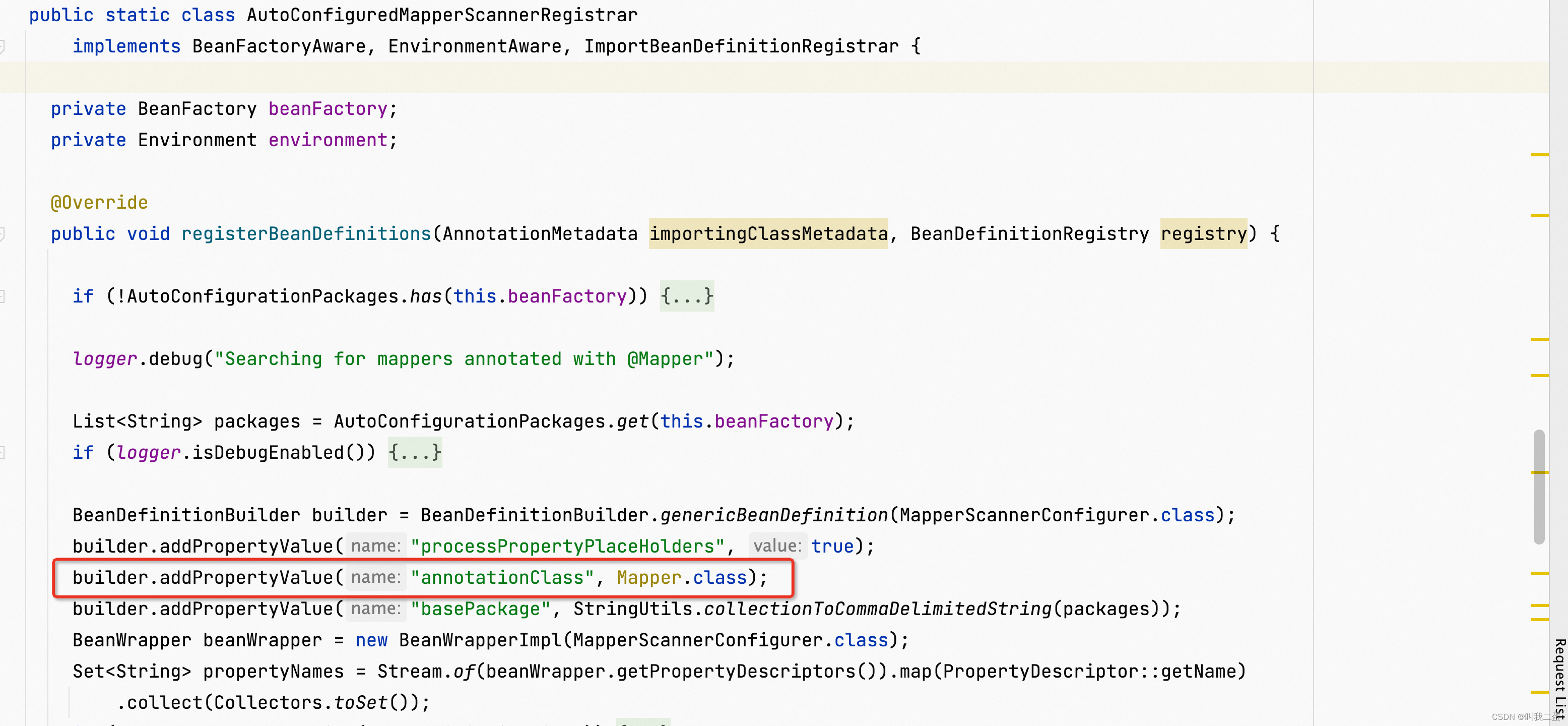
SpringBoot Starter 作用及原理
本文会以 mybatis 为例,通过对比 mybatis-spring 和 mybatis-spring-boot-starter 代码示例,了解 Starter 的作用。并对 mybatis-spring-boot-starter 进行简单剖析,了解 Starter 原理。 下面还有投票,一起参与进来吧👍…...

【rust】| 05——语法基础 | 流程控制
系列文章目录 【rust】| 00——开发环境搭建 【rust】| 01——编译并运行第一个rust程序 【rust】| 02——语法基础 | 变量(不可变?)和常量 【rust】| 03——语法基础 | 数据类型 【rust】| 04——语法基础 | 函数 【rust】| 05——语法基础 | 流程控制 文章目录 流程控制1. 条…...

解决Makefile: recipe for target ‘xxx‘ failed
author daisy.skye的博客_CSDN博客-嵌入式,Qt,Linux领域博主 问题 在android编译Kernel调用makefile引起的recipe for target 很多文章写的是由于编译文件路径引起或者是makefile代码中的空格引起的 分析 但是如果makefile文件不是手动配置的而且源代码提供的,…...

小黑子—多媒体技术与运用基础知识三:数字图形图像处理技术
多媒体技术与运用3.0 多媒体系列第三章1. 颜色科学1.1 颜色的性质1.1.1 颜色的物理性质1.1.2颜色三特性1.1.3三原色与三补色 1.2 颜色空间1.2.1 与设备无关的颜色空间1.2.1 与设备相关的颜色空间 1.3 常见的多媒体系统颜色空间1.3.1 RGB颜色空间1.3.2 CMYK颜色模型1.3.3 HSB颜色…...

Nginx实现ChatGPT API代理
文章目录 一、前言说明二、前置准备三、nginx配置三、代理域名用途 一、前言说明 本篇文章可以直接用于公司生产级的使用,所需要的资源直接改为公司级的即可平替使用文章均已通过实践应用,保证文章准确性,但因不同环境的不同可能效果不一致可…...

FileNotFoundError: [Errno 2] No such file or directory: ‘dot‘
FileNotFoundError: [Errno 2] No such file or directory: ‘dot’ 在绘制树形结构图的时候出现上述报错:已安装环境为ubuntu,python3.9 解决方案: 1、在终端输入sudo apt-get install graphviz,按回车键,输入密码&a…...

【分布族谱】正态分布和二项分布的关系
文章目录 正态分布二项分布验证 正态分布 正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。测量是人类定量认识自然界的基础,测量误差的普遍性&am…...

7.设计模式之责任链模式
前言 责任链,即将能够处理同一类请求的对象连成一条链,所提交的请求沿着链传递, 链上的对象逐个判断是否有能力处理该请求,如果能则处理,如果不能则传递给链上的下一个对象。为了避免请求发送者与多个请求处理者耦合在…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
